抓住邏輯發展節點助成數學獨特培育
——從學生獲取數學知識的思維過程談起

江蘇淮陰師范學院第一附屬小學 潘明珍

抓住邏輯發展節點助成數學獨特培育
——從學生獲取數學知識的思維過程談起

江蘇淮陰師范學院第一附屬小學 潘明珍

《義務教育數學課程標準》（2011年版）指出：學生學習應當是一個生動活潑的、主動的和富有個性的過程。因此，我認為學習活動最起碼有這樣的兩個關鍵詞：自主經歷、互動生成。可是，縱觀當下的數學教學，仍有一部分教師受到應試教育的影響，上課方式仍然是教師講，學生聽，學生的主動發展被教師的“一言堂”所代替，學生不能從“學會”的圈子里跳到“會學”，難以形成獨立思考、主動學習的核心素養，創造精神更是無從談起。要從根本上改變這種狀況，就必須改良廣大教師生長的土壤，變革教師的教法和學生的學法，通過對數學特有的邏輯系統的學習和思考，幫助學生形成主動學習的心態，使他們學會選擇、學會判斷、學會表達，提升思維品質，從而擁有自身發展的力量。

學生學習和獲取數學知識的全過程，一般可分為“發生與形成”“鞏固與深化”“建構與發展”三個階段。為了使學生真實、有效的發展，在這三個階段中，教師應注意讓學生經歷分析與綜合、比較與分類、抽象與概括、具體化與系統化等思維過程，引導他們運用概念進行判斷推理，培養初步的邏輯思維能力和自主學習能力。

一、豐富發生之初，引導“感性形成理性”。

小學生對具體材料感知達到一定數量和一定程度，抽象思維就悄悄地開始了。所以，為了幫助學生感悟新知、體驗新知，就要提供充分準備的感性材料，突出本質屬性，增強學生的感性認識，幫助他們完成從具體到抽象的概括。如長方體的體積計算公式的形成是一個抽象的過程，學生比較難理解。教學中，我引導學生經歷了如下的思考過程：

1.問題引領

教師提出猜想：同學們，長方形的面積公式，我們是怎么找到的呢？它的大小，同哪些因素有關？猜一猜，長方體體積的大小同哪些因素有關，我們該怎么去尋找呢？

通過開放問題的設計，激起每位同學主動思考的心向，并帶著這樣的思考探究，主動開始探究之旅。

2.主動學習

學生根據長方形面積公式的推導方法，主動遷移，動手實踐。他們自主選擇身邊的活動材料，分別用體積為1立方厘米的立方體填補長方體空間，并想辦法紀錄實驗的結果。同學們探究的熱情很高漲，人人投入了思考與實踐中，不少同學自主作表，整理和統計數據。

教師課前提供了許多不同規格的長方體，學生在實踐中深刻感受到長方體體積與長、寬、高有關系，猜想有了依據，學生的思考開始走向深刻。

3.自主發現

依據學生們對數據極為敏感，他們不僅發現了長方體的體積就是所用長方體總個數，還學會了下結論，提煉出既然長方體總個數等于長、寬、高三者的乘積，那么長方體體積就等于長、寬、高的乘積。在這樣的歸納、分析、概括中學生們自主發現的能力又一次得到了提升。

4.問題解決

此時，學生用這個公式試算長方體體積，驗證公式，嘗試用字母表示公式。這樣，學生在猜想、分析、比較、抽象、概括等思維過程中較好地形成了新知，實現由感性認識向理性認識的飛躍。

二、溝通內在關聯，促進“已知形成未知”。

數學知識紛繁復雜，學生也不可能都能經歷“感性形成理性”的抽象概括。這時，抓住已知與未知的內在聯系，實現知識的遷移，就成為學生獲取知識的一條捷徑。雖然它是從理性到理性的，但其進程卻反映著積極的思維活動，其實質是從已經獲得的判斷中進行邏輯推理去獲得新的判斷。

如教學分數乘法應用題，可組織如下過程，引導學生主動獲取新知：

1.問題解決、喚起經驗

新課伊始，組織學生常規積累。解答有關的整數、小數應用題，喚起相關知識，明晰數量間關系，說明問題解決的道理。

（1）有蘋果40千克，梨的重量是蘋果的3倍，梨有多少千克？

（2）有蘋果40千克，梨的重量是蘋果的1.5倍，梨有多少千克？

2.創設情境、激起沖突

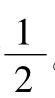
3.討論交流、形成新知

通過師生互動、生生互動，實現新舊知識的溝通，從而概括出此類問題也用乘法計算。

以上學習過程的實質是溝通整數、小數、分數應用題的聯系，基于意義關聯的角度設計課堂教學，課堂充滿了生長與發展的氣息，學生的認知結構也得到了完善和發展。

三、精選有效練習，助推“建構與發展”。

知識初步形成以后，還要設計有效的學習活動，提供變式、反例，進行比較等，經歷從特殊到一般的不完全歸納、從一般到特殊的具體演繹，使學生對知識進行更高程度的概括，從而日益深化，實現建構與發展。

1.提供相宜材料，完成“特殊到一般”

數學學習中，很多時候都經歷著“特殊到一般”的不完全歸納過程，學生通過推理獲得新發現。如“能被2、3、 5整除的數的特征”等知識，都經歷著這樣的思維過程。

再如“乘法交換律”的學習活動，學生們經歷了大量材料的積累、發現。如學生計算15×404、404×15、23× 30、30×23、80×200、200×80等算式，比較中歸納形成：a×b=b×a的公式。

2.注重說理訓練，外化“一般到特殊”

當然，學生理解概念、領會原理、掌握方法、形成新的結構群，不僅要經歷由特殊到一般的歸納過程，還要經歷回歸特殊的演繹過程。教學中，我們不能只滿足于學生說出的結論或結果是否正確，忽略對于怎樣把一般原理運用于個例的演繹推理的觀察，而應多問幾個“為什么”？要求學生說算理，則是發揮語言這一表達思維的工具的作用，完善知識、能力等建構的有效途徑。

當然，數學知識的形成與發展，是一個極其豐富、復雜的歷程，它總是與鄰近知識、事物發生著各種聯系，逐漸組建成獨特的結構或系統。時代的進步與發展，正是希望我們的數學教師，能夠憑借豐富的專業素養，引領學生把握知識間的內在聯系借助人類文明的經驗、智慧，在探究性學習活動中，學會溝通、梳理、分析、綜合，從而獲得主動思考和解決問題的內生力量。抓住了邏輯發展的節點，也就擁有了開放課堂的新質，有效地實現著數學學習的獨特培育。?