多重時滯富營養化生態模型的穩定性與分支分析

楊紀華,劉媚

(1.寧夏師范學院數學與計算機科學學院,寧夏固原756000)

(2.北京師范大學數學科學學院,北京100875)

多重時滯富營養化生態模型的穩定性與分支分析

楊紀華1,2,劉媚1

(1.寧夏師范學院數學與計算機科學學院,寧夏固原756000)

(2.北京師范大學數學科學學院,北京100875)

本文研究了多重時滯富營養化生態模型的穩定性與分支問題.利用特征值方法,分別研究了具有單時滯和雙時滯模型的線性穩定性.發現當模型中的時滯經過一系列臨界值時,模型在平衡點附近經歷了Hopf分支和Hopf-zero分支,并給出Hopf分支和Hopf-zero分支存在的充分條件.最后數值模擬驗證了理論結果.

雙時滯;穩定性;Hopf分支;Hopf-zero分支

1　引言

水體的富營養化可以導致一系列嚴重問題,比如生態完整性遭到破壞.它的特點是藻類大量繁殖,其它水生物大量減少.浙江省溫州市澤雅水庫處于副熱帶地區,由于藻類大量繁殖造成過濾系統堵塞,導致數以百萬計的人的飲用水危機.水體富營養化的去除主要有物理化學和生物處理兩種方法[1].為了更好的控制水體富營養化等污染狀態出現,有必要對水體中生態系統進行研究[2-4].澤雅水庫富營養化過程與水體中的藻類數量密切相關,同時也與水體中的濾食性魚類(如鰱魚和鳙魚)相關.為了能更好的應用生物學原理控制澤雅水庫的富營養化,基于文獻[5],于恒國,趙敏等在文獻[6]中考慮了兩種濾食性魚類鰱魚和鳙魚,提出了一個新的模型如下

其中x(t)表示t時刻藻類的數量,y(t)和z(t)分別表示t時刻濾食性魚類鰱魚和鳙魚的數量,r表示藻類的內稟增長率,αi(i=1,2)分別表示鰱魚和鳙魚的投放率,ei(i=1,2)分別表示鰱魚和鳙魚轉化為消費者的比率,k表示x(t)的承受力,δi(i=1,2)分別表示鰱魚和鳙魚的飽和常數,ρi(i=1,2)分別表示鰱魚和鳙魚的相互影響因子,mi(i=1,2)分別表示鰱魚和鳙魚的死亡率,γ表示鰱魚的相對優勢,τ、τ1和τ2是正時滯.

在文獻[6]中,作者給出了方程(1.1)的平衡點穩定的充分條件,并用數值模擬的方法對方程(1.1)進行了詳細的研究.本文中取τ1=τ2=σ,從穩定性與分支的角度研究系統(1.1),對該系統的平衡點穩定性、Hopf分支和Hopf-zero分支的存在性進行分析．

2　平衡點的穩定性和分支的存在性

顯然,S0=(0,0,0)和S1=(k,0,0)始終是系統(1.1)的平衡點.平衡點S0表示水體中藻類、鰱魚和鳙魚都不存在.平衡點S1表示水體中藻類存在,而鰱魚和鳙魚不存在.在一定條件下,系統(1.1)還有其它平衡點.

(1)當γe1α1＞0,kγe1α1＞m1(k+δ1)時,系統(1.1)存在平衡點S2=(x2,y2,0),其中

此時水體中只有藻類和鰱魚存在,鳙魚不存在.

(2)當e2α2＞m2,ke2α2＞m2(k+δ2)時,系統(1.1)存在平衡點S3=(x3,0,z3),其中

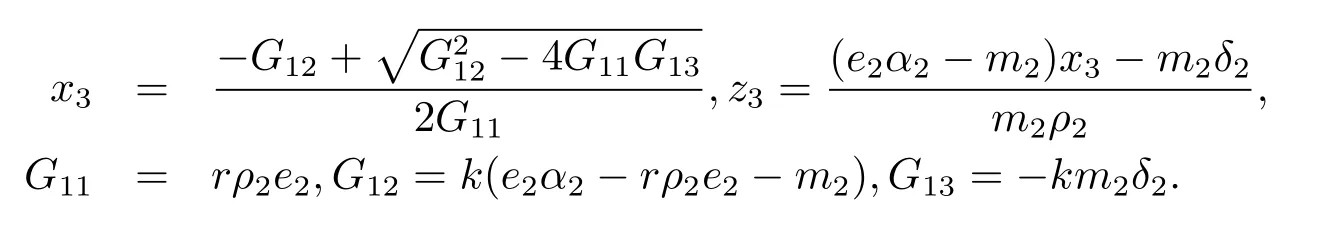
此時水體中只有藻類和鳙魚存在,鰱魚不存在.

(3)當

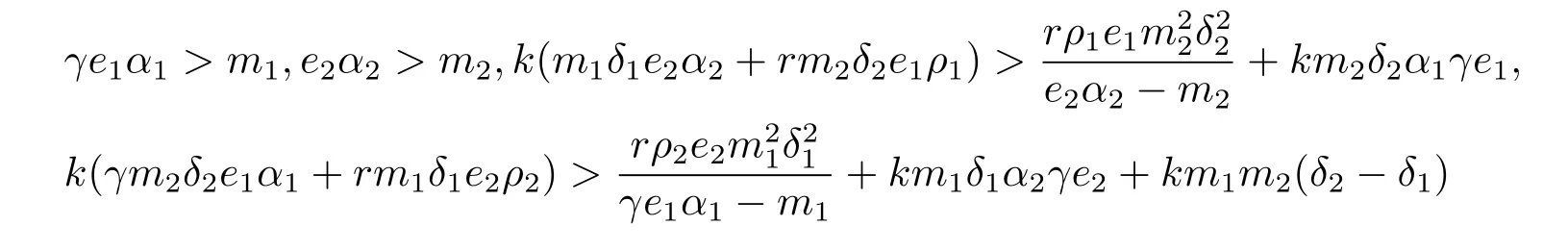
時,系統(1.1)存在平衡點S4=(x4,y4,z4),其中

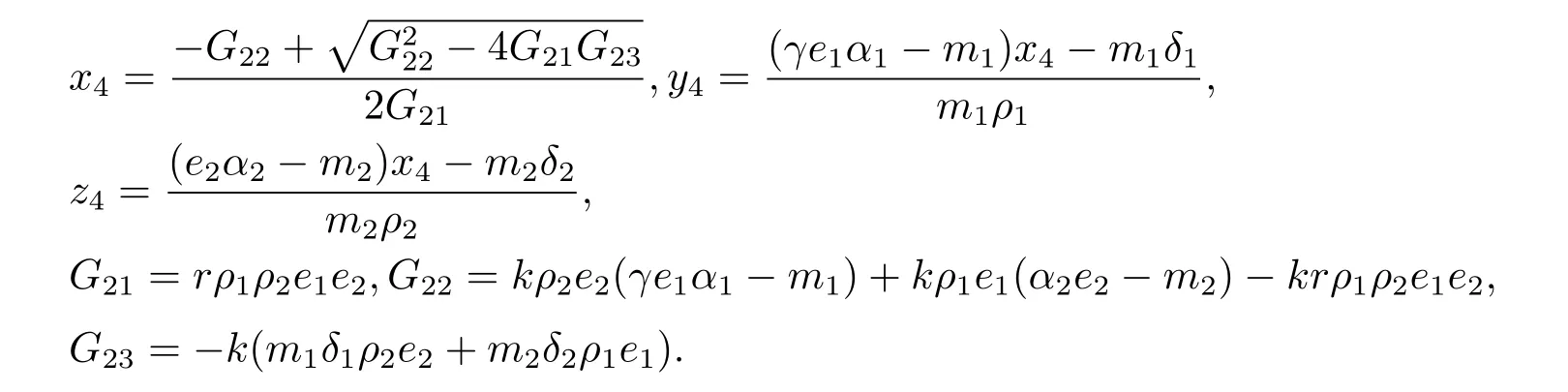
此時水體中藻類同濾食性魚類鰱魚和鳙魚共存.

不失一般性,本文只討論平衡點S4.系統(1.1)在平衡點S4處的特征方程為

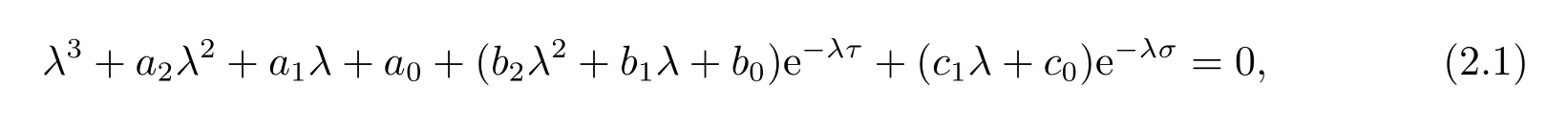
其中

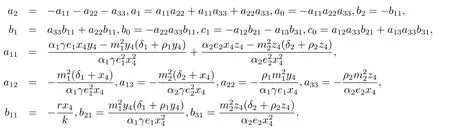
注特征方程(2.1)是一個超越方程,研究起來比較復雜.據作者了解,目前還沒有研究類似于方程(2.1)的文獻.

2.1τ=0,σ=0的情形

此時方程(2.1)變為

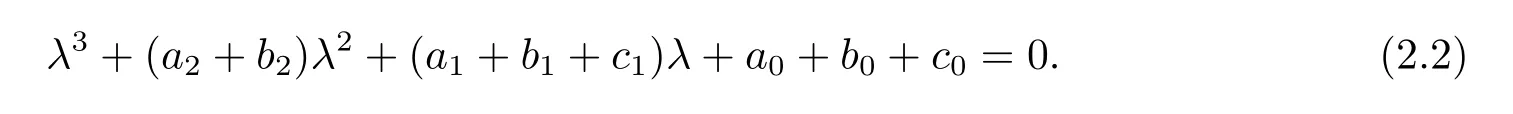
根據微分方程的定性理論以及Hurwitz判據[7],可得如下引理.

引理2.1(i)當a0+b0+c0=0時,λ=0是方程(2.2)的根;當a0+b0+c0=0, a1+b1+c1＞0,且a2+b2＞0時,方程(2.2)有一個零根和兩個具有負實部的根.此時,系統(1.1)經歷了不動點分支;

(ii)當a2+b2＞0,a0+b0+c0＞0,(a2+b2)(a1+b1+c1)＞a0+b0+c0時,方程(2.2)的所有根具有負實部.

作如下假設

(H1)a2+b2＞0,a0+b0+c0＞0,(a2+b2)(a1+b1+c1)＞a0+b0+c0.

此時方程(2.1)變為

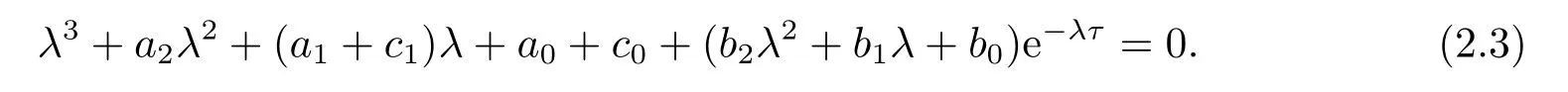
顯然,iβ(β＞0)是方程(2.3)的根當且僅當β滿足

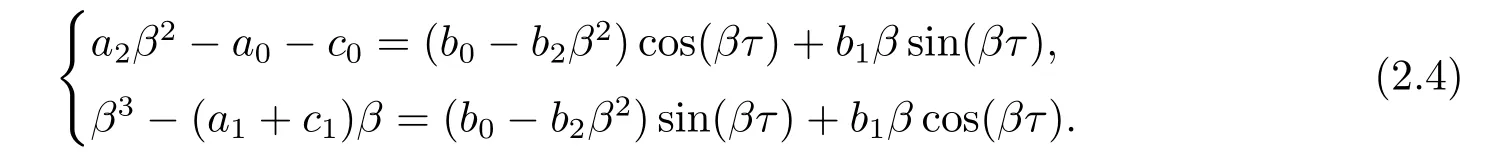
平方相加,并令ξ=β2可得

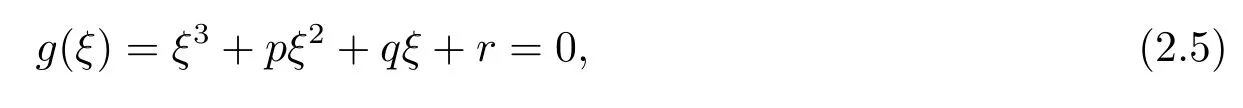
其中

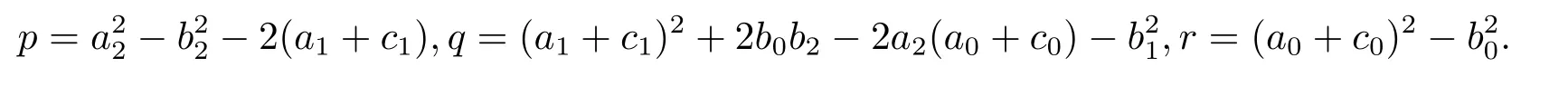
引理2.2(i)當r＜0時,方程(2.5)至少有一個正實根;

(ii)當r≥0且p2≤3q時,方程(2.5)沒有正實根;

(iii)當r≥0且p2＞3q時,方程(2.5)有正實根的充要條件是z?=＞0且 g(z?)≤0,其中?=p2-3q.

(iii)如果r≥0且?＞0,3ξ2+2pξ+q=0有兩個實根z?=和ξ?=

充分性因為g＇＇(z?)=＜0,即z?是g(ξ)的極小值點,ξ?是g(ξ)的極大值點.又g(ξ)=∞,所以當z?＞0且g(z?)≤0時,方程(2.5)有正實根.

必要性否則,假設z?≤0或者z?＞0且g(z?)＞0.因為函數g(ξ)在[z?,∞)上單調增加,且g(0)=r＞0,所以當z?≤0時方程(2.5)無正實根.矛盾.因為ξ?是g(ξ)的極大值點,所以g(z?)＜g(ξ?),且g(0)=r＞0,所以當z?＞0且g(z?)＞0時方程(2.5)無正實根.矛盾.引理2.2得證.

作如下假設

(H2)r≥0,p2≤3q;

(H3)r＜0;

(H4)r≥0,p2＞3q,z?=＞0且g(z?)≤0.

不失一般性,假設方程(2.5)有三個正實根ξ1,ξ2和ξ3.所以方程(2.3)有三個正實根(k=1,2,3).記

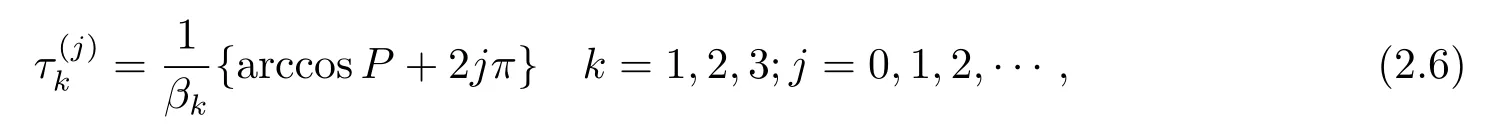
其中

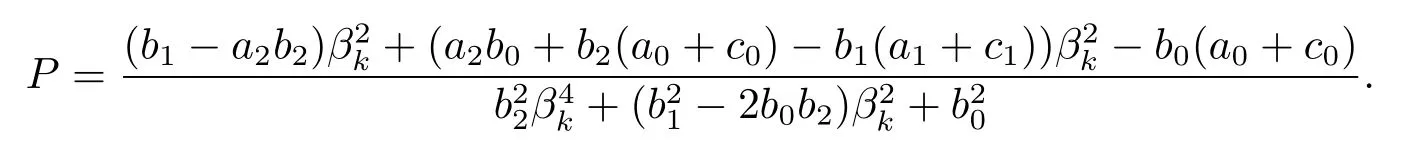
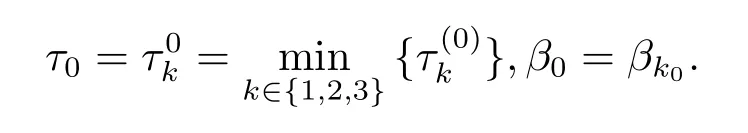
引理2.3[8]設

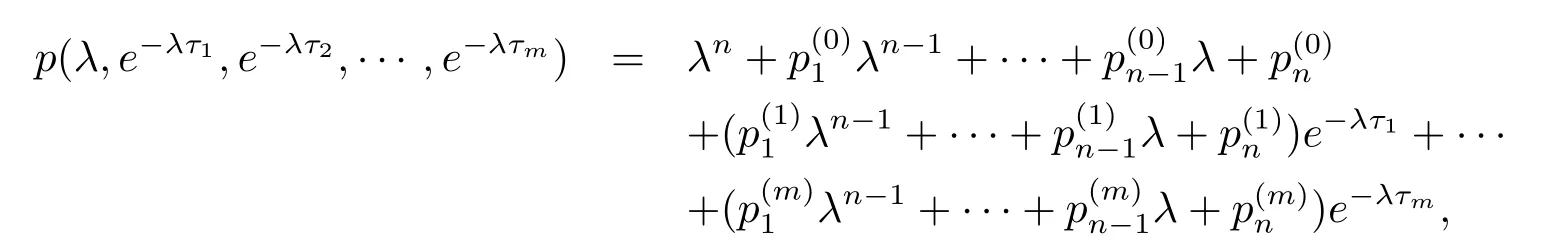
其中τi≥0(i=1,2,···,m),(i=0,1,···,m;j=1,2,···,n)是常數,則當τ1,τ2,···,τm變化時,p(λ,e-λτ1,e-λτ2,···,e-λτm)位于右半平面的零點重數之和只有當虛軸上出現零點或有零點穿過虛軸時才發生變化.

由引理2.2和引理2.3可得下面引理.

引理2.4假設(H1)成立.

(i)如果(H2)成立,則當τ≥0時,方程(2.3)的根都具有負實部;

由隱函數定理,存在ε0＞0,使得當|τ-|＜ε0時,方程(2.3)有一對虛根λ(τ)= α(τ)±iβ(τ),且滿足α()=0,β()=βk(k=1,2,3).

證把λ(τ)代入方程(2.3)并對τ求導可得

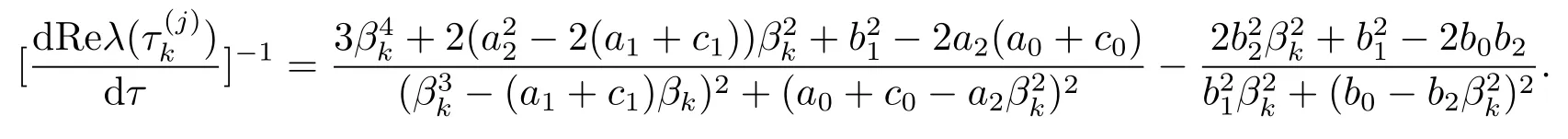
由(2.4)式可得

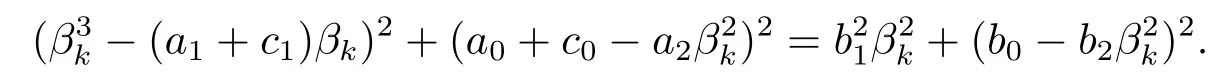
因此

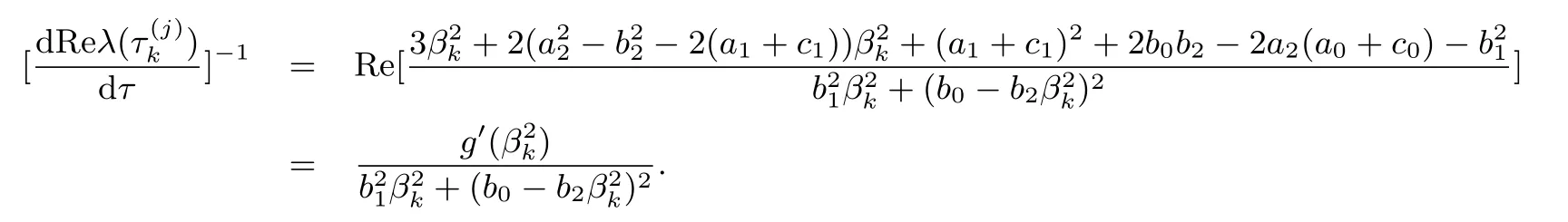
定理2.1假設(H1)成立.

(i)如果(H2)成立,則當τ≥0時,系統(1.1)的平衡點S4是局部漸近穩定的;

(ii)如果(H3)或者(H4)成立,則當τ∈[0,τ0)時,系統(1.1)的平衡點S4是局部漸近穩定的.而且如果0,則當τ=時,系統(1.1)在平衡點S4處經歷了Hopf分支.

證由引理2.3可得(i)和(ii)的前半部分正確.由文獻[9]中關于泛函微分方程的Hopf分支定理可得(ii)的后半部分正確.定理2.1得證.

引理2.6如果a0+b0+c0=0,a1+b1+c1＞0,a2+b2＞0,并且(H4)成立,則當τ∈[0,τ0)時,方程(2.3)除了有一個零根外,其余根都具有負實部.

證因為a0+b0+c0=0,所以0是方程(2.3)的根.由引理2.4可知,方程(2.3)沒有純虛根.

用反證法.令a0+b0+c0=a,假設存在τ?∈(0,τ0)使得方程(2.3)有實部為正的根,記為λ0=υ0+iζ0,設λ(a,τ)=υ(a,τ)+iζ(a,τ)是方程(2.3)的根,且滿足υ(a=0,τ?)= υ0＞0,ζ(a=0,τ?)=ζ0.因為υ(a,τ)關于a連續,則存在κ1＞0,當a∈(0,κ1)時, υ(a,τ?)＞0.又τ0(a)=τ0,所以對0＜γ0≤τ0-τ?,存在κ2＞0,當a∈(0,κ2)時,使得|τ0(a)-τ0|＜γ0,進而可得τ?∈(0,τ0(a)).取κ=minκ1,κ2,則當a∈(0,κ)時,υ(a,τ?)＞0且τ?∈(0,τ0(a)).又由引理2.4,當a∈(0,κ)方程(2.3)的根都具有負實部.這是一個矛盾.引理2.6得證.

定理2.2如果a0+b0+c0=0,a1+b1+c1＞0,a2+b2＞0,并且(H4)成立,則當τ=τ0時,方程(2.3)除了有一個零根和一對純虛根±iβ0外,其余根都具有負實部.此時系統(1.1)在平衡點S4處經歷了Hopf-zero分支.

證因為a0+b0+c0=0,所以0是方程(2.3)的根.由引理2.4可知±iβ0也是方程(2.3)根.假設當τ=τ0時,方程(2.3)有一個根具有正實部,記為λ0=υ0+iζ0.λ(τ)=υ(τ)+iζ(τ)是方程(2.3)的根,且滿足υ(τ0)=υ0＞0,ζ(τ0)=ζ0.因此當τ→時,方程(2.3)有具有正實部的根,這與引理2.6矛盾.定理2.2得證.

本小節中,固定τ,以σ為參數,且τ取值于使方程(2.3)的根都具有負實部的區間.設iω(ω＞0)是方程(2.1)的根,則可得

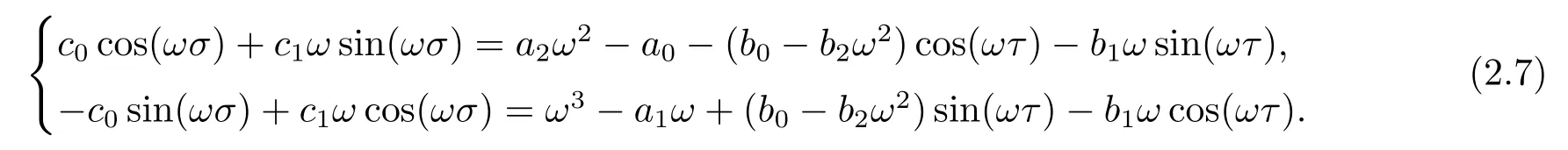
把(2.7)式中兩個方程平方相加可得

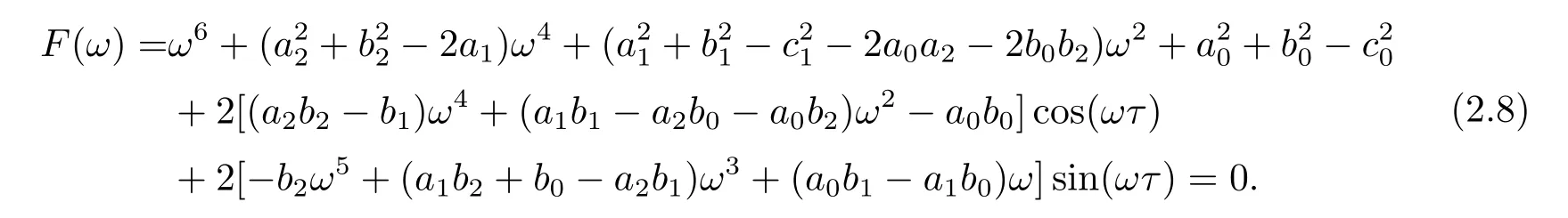
假設方程(2.8)有有限個正根ω1,ω2,···,ωs.則與每個ωk(k=1,2,···,s)相對應的為

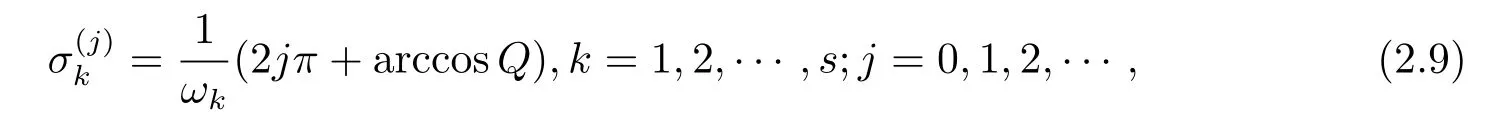
其中

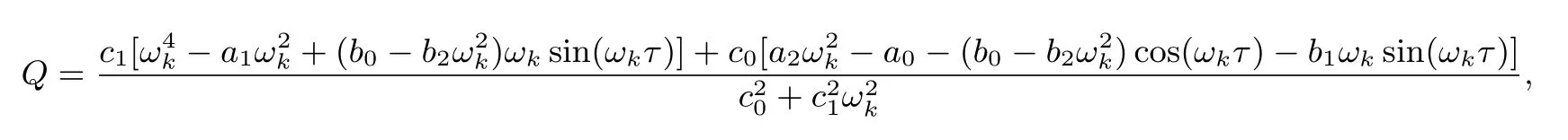
則(ωk,)是方程(2.7)的根.由此可得如下引理2.7.

定義

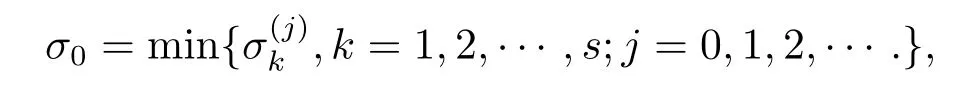
并記與之相對應的ωj為ω0.假設λ(σ)=α(σ)+iω(σ)是特征方程(2.1)在σ=附近的根,且滿足α(σ0)=0,ω(σ0)=ω0.

其中

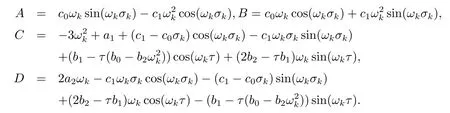
證方程(2.1)兩端同時關于σ求導可得

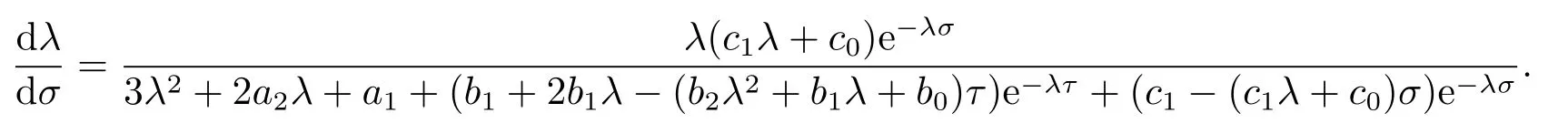
通過直接而繁瑣的計算可得

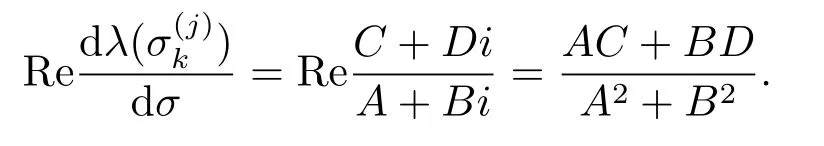
由本文引理2.1至引理2.8和文獻[9]中第11章的定理1.1,可以得到下面關于系統(1.1)的平衡點的穩定性與Hopf分支的存在性定理.

定理2.3假設(H1)成立,

(i)如果(H2)成立且F(ω)沒有正根,則當σ≥0時,系統(1.1)的平衡點S4是局部漸近穩定的;如果(H2)成立且F(ω)有正根,則當σ∈[0,σ0)時,系統(1.1)的平衡點S4是局部漸近穩定的;在后一種情況,如果AC+BD0,則當σ=(k=1,2,···,s;j=0,1,2,···)時,系統(1.1)在平衡點S4處經歷了Hopf分支.

(ii)如果(H3)或(H4)成立,τ∈[0,τ0),且F(ω)沒有正根,則當σ≥0時,系統(1.1)的平衡點S4是局部漸近穩定的;如果(H3)或(H4)成立,τ∈[0,τ0),且F(ω)有正根,則當σ∈[0,σ0)時,系統(1.1)的平衡點S4是局部漸近穩定的;在后一種情況,如果AC+BD0,則當σ=(k=1,2,···,s;j=0,1,2,···)時,系統(1.1)在平衡點S4處經歷了Hopf分支.

綜合上面的討論可得關于系統(1.1)的Hopf-zero分支的存在定理.

定理2.4假設a0+b0+c0=0,a1+b1+c1＞0,a2+b2＞0,且方程(2.8)至少有一個正實根ωk(k=1,2,···,s),

(i)如果(H2)成立,則當σ=σ0時,系統(1.1)在平衡點S4附近經歷了Hopf-zero分支;

(ii)如果(H4)成立,τ∈[0,τ0),則當σ=σ0時,系統(1.1)在平衡點S4附近經歷了Hopf-zero分支.

證因為a0+b0+c0=0,所以0是方程(2.1)的根.由引理2.7可得,±iσ0是方程(2.1)的一對純虛根.類似于定理2.2的證明可得,當σ=σ0時,方程(2.1)除了一個零根和一對純虛根±iσ0外,其余根均具有負實部,即系統(1.1)在平衡點S4附近經歷了Hopf-zero分支.定理2.4得證.

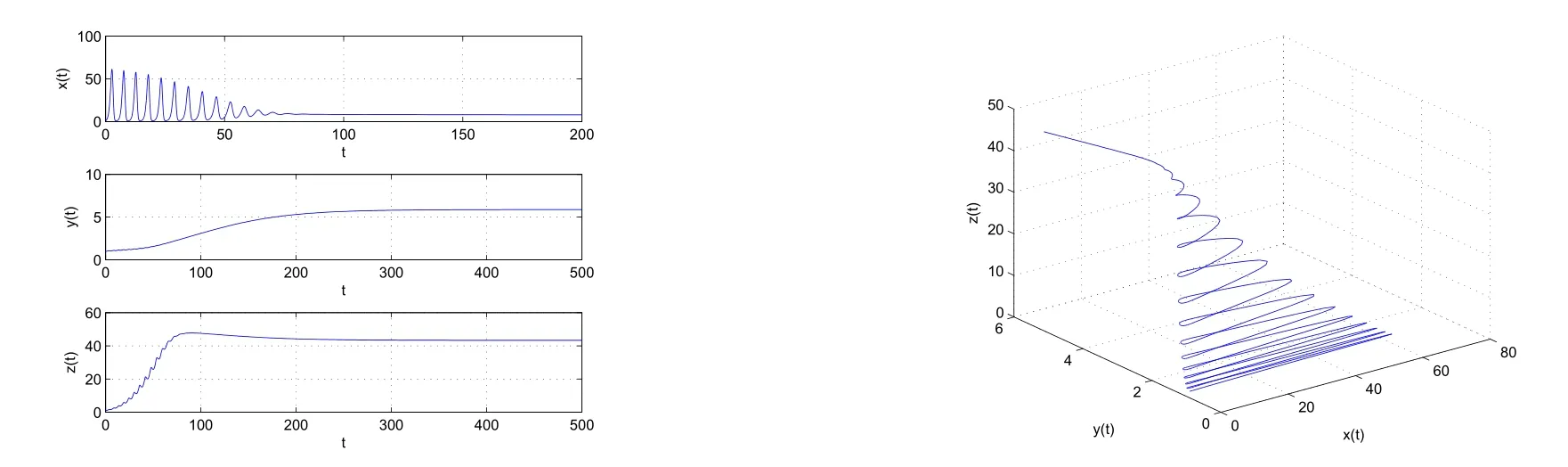
圖1:當τ=1.01時,系統(1.1)的平衡點S4局部漸近穩定.

圖2:當τ=1.4時,系統(1.1)在平衡點S4附近經歷了Hopf分支.

3　數值模擬

為了研究具多重時滯水體富營養化生態模型的復雜動力學行為,本文應用微分方程的穩定性和分支理論得到了平衡點的穩定性區域和周期解存在的充分條件.為了說明理論結果的正確性,下面進行數值模擬.

參照文獻[6]中的數據,取r1=2.1,k=20,e1=0.45,e2=0.5,a1=0.8,a2= 0.6,β=0.35,b1=0.25,b2=2.5,c1=0.25,c2=0.55,m1=m2=1.通過計算知(H1)和(H3)滿足,g(ξ)有一個正根ξ1≈1.18,所以β1≈1.0861,g＇()＞0.由(2.6)式和引理2.5可得

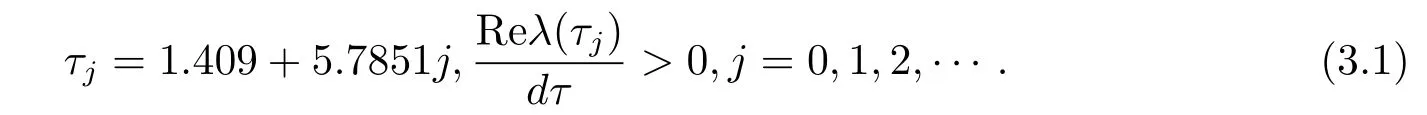
所以計算可得τ0=1.409.因此由定理2.1和(3.1)式可得如下結論.

結論3.1假設τj(j=0,1,2,···)如(3.1)式定義,

(i)當τ∈[0,τ0)時,系統(1.1)的平衡點S4是局部漸近穩定的(如圖1所示);

(ii)當τ=τj(j=0,1,2,···)時,系統(1.1)在平衡點S4處經歷了Hopf分支(如圖2所示).

4　結論

本文研究了基于浙江省溫州市澤雅水庫的雙時滯富營養化生態模型.通過對系統線性化方程的特征方程根的分布分析入手,得出了系統的線性穩定性區域,當時滯經歷一系列臨界值時,系統經歷了Hopf分支和Hopf-zero分支.本文研究表明,時滯在系統(1.1)的復雜動力學行為中起了重要作用,時滯可以使得藻類和濾食性魚類(鰱魚和鳙魚)在穩定狀態下共存.即時滯對生態種群的穩定性有積極影響.

[1]Lee C G,Fletcher T D,Sun G Z.Nitrogen removel in constructed wetland systems[J].Eng.Life Sci.,2009,9:11-22.

[2]Shukla J B,Misra A K,Chandra P.Mathematical modeling and analysis of the depletion of dissolved oxygen in eutrophied water bodies affected by organic pollutants[J].Nonl.Anal.:Real World Appl., 2008,9:1851-1865.

[3]Alvarez L J,Fernandez F J,Munoz R.Mathematical analysis of a three-dimensional eutrophication model[J].J.Math.Anal.Appl.,2009,349:135-155.

[4]張艷紅.三種群的競爭系統全局解的一致有界性[J].數學雜志,2012,32(6):1129-1135.

[5]Xiu P,Liu J.Practical success of biomanipulation using filter-feedings fish to control syanobacteria blooms a synthesis of decades of research and application in a subtropuical hypertrophic lake[J]. Sci.World,2001,1:337-356.

[6]Yu H G,Zhao M,Agarwal R P.Stability and dynamics analysis of time delayed eutrophication ecological model based upon the Zeya reservoir[J].Math.Comput.Simul.,2014,97:53-67.

[7]馬知恩,周義倉.常微分方程定性與穩定性方法[M].北京:科學出版社,2001.

[8]Ruan S,Wei J.On the zeros of transcendental functions to stability of delay differential equations with two delays[J].Dyn.Contin.Discrete Impuls.Syst.A Math.Anal.,2003,10:863-874.

[9]Hale J K,Lunel S V.Introduction to functional differential equation[M].New York:Springer-Verlag, 1993.

2010 MR Subject Classification:34C23

STABILITY AND BIFURCATION ANALYSIS OF MULTIPLE TIME DELAY EUTROPHICATION ECOLOGICAL MODEL

YANG Ji-hua1,2,LIU Mei1
(1.School of Mathematics and Computer Science,Ningxia Normal University,Guyuan 756000,China)
(2.School of Mathematical Science,Beijing Normal University,Beijing 100875,China)

In this paper,the stability and bifurcation problem of eutrophication ecological model with two time delays is studied.By using the eigenvalue method,we study the linear stabilities with one delay and two delays,respectively.It is found that Hopf bifurcations and Hopf-zero bifurcations exist at the equilibriums when the delays pass through a sequence of critical values.The sufficient conditions of the existence of Hopf bifurcation and Hopf-zero Bifurcation are obtained.In the end,some numerical simulations are carried out for supporting the analytic results.

two time delays;stability;Hopf bifurcation;Hopf-zero bifurcation

MR(2010)主題分類號:34C23O175

A

0255-7797(2016)06-1222-09

?2015-02-10接收日期:2015-07-06

國家自然科學基金資助(11361046);寧夏自然科學基金(NZ13213);寧夏高等學校科研項目(寧教高[2014]222號(17);寧教高[2014]222號(16)).

楊紀華(1983-),男,河南周口,講師,主要研究方向:微分方程的穩定性與分支理論.