“勾股定理”之我見
常州市武進區遙觀初級中學八(4)班 張 健
“勾股定理”之我見
常州市武進區遙觀初級中學八(4)班張健
email:czsshy@126.com
上課時,老師講了多種關于“勾股定理”應用的數學思想,我聽了之后,很是受用.在解題過程中,我又發現,除了老師講的知識外,在《勾股定理》這一章中,還滲透著化歸的思想.下面我就以學習過程中遇到的題目為例,跟大家分享一下我的發現吧!
一、化歸
原題:如圖4-1,有一圓柱體,它的高為16cm,底面半徑為4cm,在圓柱的下底面點A處有一個蜘蛛,它想吃到上底面上與點A相對的點B處的蒼蠅,需要爬行的最短路徑是多少cm(π取3)?
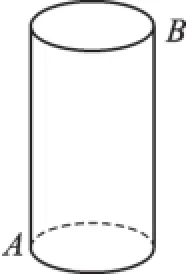
圖1
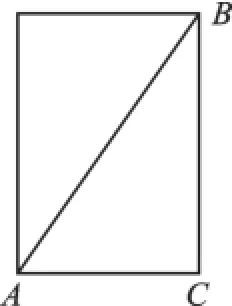
圖2
蜘蛛在圓柱側面上爬行,所以這道題是求幾何體表面的最短距離,這就需要把圓柱的側面展開.這樣就把問題轉化成了平面上兩點間距離最短的問題,即化“曲面”為“平面”.如圖2,把圓柱的側面展開,即為長方形,根據“兩點之間線段最短”可知,線段AB的長即為蜘蛛爬行的最短路徑.其中BC的長等于圓柱的高16cm,AC的長等于圓柱底面周長的一半12cm.由勾股定理,在Rt△ABC中得,AB2=AC2+BC2,則AB=20.
由于這道題用到了剛學習的勾股定理,所以我印象深刻,化歸思想也印在了我的腦海里,不久后,我發現,這樣類型的題還真不少.
同類題型:如圖3,有一個長方體紙箱,長是60cm,寬和高都是40cm.一只螞蟻從頂點A沿紙箱表面爬到頂點B,它所爬行的最短路線的長是多少cm?
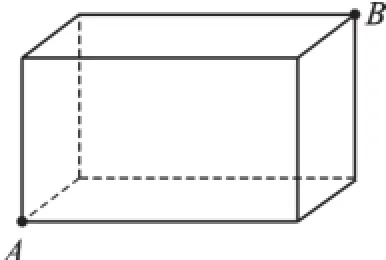
圖3
這道題中除了化歸的思想方法外,還要運用分類討論的思想方法.把紙箱六個面分別記為“前、后、左、右、上、下”,則螞蟻爬行的路線可分四種:“前”+“上”,“前”+“右”,“左”+“上”,“左”+“后”.看來只要我留心一點,這類題目對我來說就有規可循了!
數學知識奇妙無比,如果我們學習時注意歸納反思,那么一定能使自己的學習更上一層樓!
(指導教師:戚靜宇)
責任編輯:沈紅艷見習編輯:李詩

