勾股定理的起源與發展

顧金峰

勾股定理的起源與發展

顧金峰

email：czsshy@126.com

勾股定理是數學的一個基本定理，是幾何學中的明珠，既重要又簡單.其簡單表述為：直角三角形兩直角邊的平方和等于斜邊的平方．

關于勾股定理的起源，各國各民族都有不同的記載.據西方的文字記載，畢達哥拉斯于公元前550年發現了該定理.在中國，西漢的數學著作《周髀算經》中記錄的商高同周公的一段對話描述了勾股定理的由來，由于勾股定理的內容最早見于商高的話語中，所以人們也把這個定理叫做“商高定理”.看來，我國古代的人民早在幾千年以前就已經發現并應用勾股定理了．

關于勾股定理的名稱，在我國，以前叫畢達哥拉斯定理，這是隨西方數學傳入時翻譯的名稱.20世紀50年代，學術界曾展開過關于這個定理命名的討論，最后用“勾股定理”，得到教育界和學術界的普遍認同.1993年，全國自然科學名詞審定委員會公布數學名詞，確定這一定理的漢文名稱為勾股定理，其對應的英文名是Pythagoras theorem，注釋中說：“又稱‘畢達哥拉斯定理’.曾用名‘商高定理’.”至此，“勾股定理”成為我國確立的標準名稱.

勾股定理在幾何學中，充滿著無限魅力，千百年來，人們對它的證明趨之若鶩，其中有著名的數學家，也有業余數學愛好者，有普通的老百姓，也有尊貴的政要權貴，甚至還有國家總統.1940年，一本名為《畢達哥拉斯命題》的勾股定理的證明專輯出版了，其中收集了367種不同的證明方法.實際上還不止這么多，有資料表明，關于勾股定理的證明方法已有500余種，僅我國清末數學家華蘅芳就提供了20多種精彩的證法.這是任何定理無法比擬的.在這數百種證明方法中，有的十分精彩，有的十分簡潔，有的因為證明者身份的特殊而非常著名.下面我們就來介紹一下其中的4種著名的勾股定理證法.

法1——弦圖法

用四個全等的直角三角形可以拼成如圖1所示的大正方形，這個圖形被稱為“弦圖”，最早是由三國時期的數學家趙爽在為《周髀算經》作注時給出的.弦圖中每一個直角三角形涂朱色，它們的面積叫做“朱實”，中間的一個小正方形涂黃色，它的面積叫做“中黃實”，也叫“差實”，以弦為邊的大正方形面積叫做“弦實”，“按弦圖，又可以勾股相乘為朱實二，倍之為朱實四，以勾股之差自相乘為中黃實，加差實，亦成弦實.”也就是

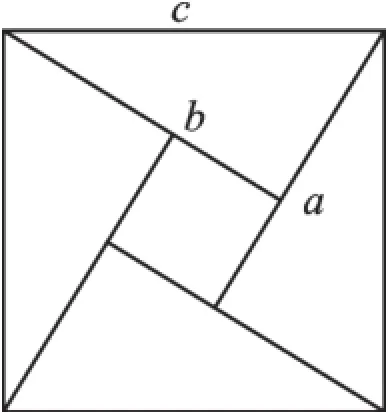
圖1

法2——面積剖分法

據傳這是當年畢達哥拉斯發現勾股定理時做出的證明.用四個全等的直角三角形可以拼成圖2，也可以拼成圖3，這兩個大正方形的邊長都為（a+b），面積相等.把這兩個圖形中的四個直角三角形除去后，剩余部分的面積應該相等，即圖2中的c2等于圖3中a2與b2的和，也就是a2+b2=c2.

圖2

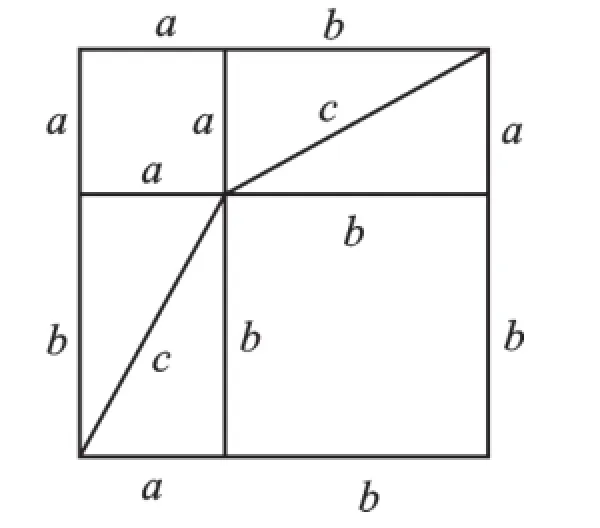
圖3

法3——總統證法

1876年一個周末的傍晚，在美國首都華盛頓的郊外，有一位中年人正在散步，欣賞黃昏的美景，他就是當時美國俄亥俄州共和黨議員伽菲爾德.他走著走著，突然發現附近的一個小石凳上，有兩個小孩正在聚精會神地談論著什么，時而大聲爭論，時而小聲探討.好奇心使然，伽菲爾德循聲向兩個小孩走去，想搞清楚兩個小孩到底在干什么.只見一個小男孩正俯著身子用樹枝在地上畫著一個直角三角形.于是伽菲爾德便問他們在干什么，那個小男孩頭也不抬地說：“請問先生，如果直角三角形的兩條直角邊分別為3和4，那么斜邊長為多少呢？”伽菲爾德答道：“是5呀.”小男孩又問道：“如果兩條直角邊長分別為5和7，那么這個直角三角形的斜邊長又是多少？”伽菲爾德不假思索地回答道：“那斜邊的平方一定等于5的平方加上7的平方.”小男孩又說：“先生，你能說出其中的道理嗎？”伽菲爾德一時語塞，無法解釋了，心里很不是滋味.于是，伽菲爾德不再散步，立即回家，潛心探討小男孩給他出的難題.他經過反復思考與演算，終于弄清了其中的道理，并給出了簡潔的證明方法.

如圖4，梯形由三個直角三角形組合而成，利用面積公式列出代數關系式：化簡后就是a2+b2= c2.

5年后，伽菲爾德就任美國第二十任總統.后來，人們為了紀念他這種直觀、簡捷、易懂的證明方法，就把這一證法稱為勾股定理的“總統證法”，這在數學史上傳為佳話.

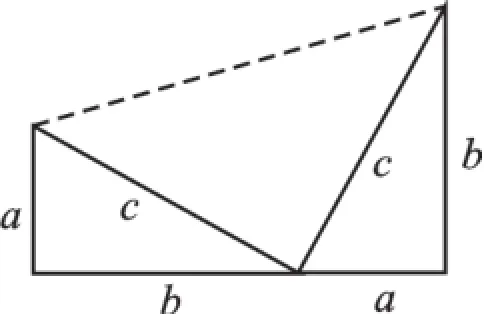
圖4

法4——歐幾里得法

圖5是歐幾里得編纂的《幾何原本》中證明勾股定理的方法，四邊形ABFE、AJKC、BCIH分別是以Rt△ABC的三邊為一邊的正方形.過C點作AB的垂線，交AB于點D，交FE于點G，連接HA、CF.通過證明△ABH≌△FBC（SAS），可得△ABH與△FBC等面積，而正方形BCIH的面積=BH·HI=2△ABH的面積，矩形BFGD的面積=BF·FG=2△FBC的面積，得到正方形BCIH與矩形BFGD等面積，同理正方形AJKC與矩形DGEA也等面積，所以正方形ABFE的面積=矩形BFGD的面積+矩形DGEA的面積，即正方形ABFE的面積=正方形BCIH的面積+正方形AJKC的面積，于是推得AB2=AC2+BC2，也就是a2+ b2=c2.證明嚴謹，反映了勾股定理的幾何意義.

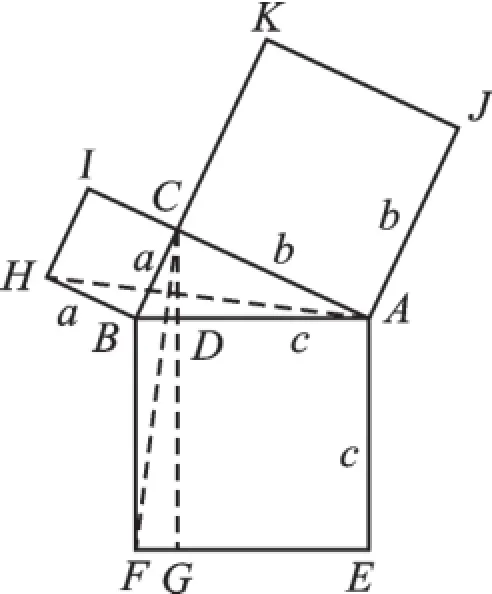
圖5

證明中的剖分法、割補法、拼拆法等蘊涵著進與退、分與合、動與靜、變與不變、數與形、正向與逆向、直接與間接的辯證思想方法，不僅能加深我們對勾股定理的認識，而且能引導大家感悟中西方數學家不同的思維特點.從文化的角度對各種證法作比較和欣賞.這些方法不僅驗證了勾股定理，而且豐富了人們研究數學問題的方法和策略，促進了數學的發展.

2002年國際數學家大會在北京召開，為弘揚我國古代數學文明，大會選用了“弦圖”作為會標的中心圖案，如圖6.

圖6

徐利治先生認為：“數學美包括數學概念的簡單性、統一性，結構系統的協調性、對稱性，數學命題和數學模型的概括性、典型性和普通性，還有數學的奇異性.”勾股定理中蘊涵著豐富的數學美，在學習中同學們要善于發現美、欣賞美，并在美的指引下不斷去探索與發現，這也是數學文化教育的一種體現.

勾股定理的圖形很美.“弦圖”簡潔大方，像一只轉動的風車，體現了圖形的對稱美.1995年，希臘專門為紀念畢達哥拉斯定理發行了一枚紀念郵票（圖7），充分展現了數學圖形和公式美的統一，將這一圖案不斷地延續下去，得到動態美麗的“勾股樹”（圖8），如數學文化的生命之樹，生生不息.

數理哲學家羅素說：“數學如果正確看待它，不但擁有真理，而且具有至高的美.”數學家華羅庚認為勾股定理可以作為人類探尋“外星人”、與“外星人”溝通的語言，因為勾股定理的圖形語言是客觀存在的（圖9）.

圖7

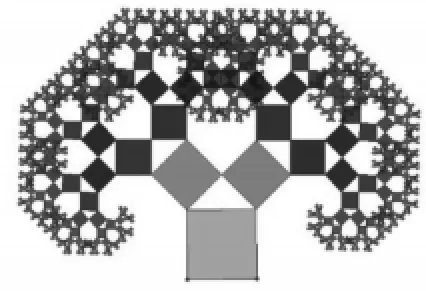
圖8

圖9

數學文化教育在傳播數學知識的同時，還傳播數學思想、方法、精神和文化，培養同學們求真、求善、求美、創新、探索的精神.揭示數學文化中所蘊涵的哲學、美學、文學和語言學等文化基因，使大家能受到良好的文化熏陶.

(作者單位：江蘇省武進區禮河實驗學校）

責任編輯：沈紅艷見習編輯：李詩