整理易錯環節提升解題能力

黃欲涵

整理易錯環節提升解題能力

黃欲涵

學習就是不斷與“錯誤”斗爭的過程，有時我們還得感謝“錯誤”，也是這些“錯誤”將我們的數學學習推送到一個更高的層次.

從全等圖形到相似圖形，是數學學習的一次飛躍，在學習過程中常常會出現一些解答錯誤，究其原因就是對相似圖形中的一些定義、定理理解不清，對一些常用的基本思想方法掌握不牢.下面就和同學們一起來剖析那些學習中所出現的部分典型錯誤.

一、乘積式和比例式的互換

【析錯】錯誤的原因是沒有掌握乘積式和比例式的互換，我們根據比例的基本性質，乘積式轉化為比例式記住一句話“左比右等于右比左”，例4y=3x，那么“左面的y比右面的x，等于右面的3比左面的4”.

二、相似三角形中對應頂點（邊）的確定

圖1

【析錯】當△ABC與△ADE相似時，這兩個三角形的對應邊成比例.但題中已知條件不是這兩個三角形的對應邊，還需轉化到

例3如圖2，在四邊形ABCD中，AD∥BC，圖中有幾對相似的三角形，請說明理由.

圖2

【錯解】有兩對相似的三角形，△AOD∽△COB，△AOB∽△DOC.

【析錯】有不少的同學為什么會發現有兩對三角形相似呢？這些同學錯誤的原因是由△AOD∽△COB得到，再得到，加上∠AOB=∠COD，所以△AOB∽△DOC.但看清一下這個比例式是不是這兩個三角形相似的比例式呢？不是.而是，所以△AOB與△DOC不相似.所以只有一對，即△AOD∽△COB.

三、相似三角形的面積比等于相似比的平方

例4如圖3，在四邊形ABCD中，AD∥BC，∠B=∠ACD=90°，AB=2，DC=3，則△ABC與△DCA的面積比為（）

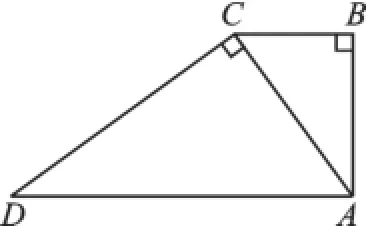
圖3

【錯解】選A.

【析錯】由AD∥BC我們可以得到∠BCA=∠CAD，題中∠B=∠ACD=90°，可以由兩角對應相等得到△ABC∽△DCA，根據相似三角形的面積比等于相似比的平方得到△ABC與△DCA的面積比為4∶9，同學們錯選的原因就是沒有弄清三角形相似的性質，把面積比等于相似比的平方，記成了面積比等于相似比.

四、位似圖形畫在位似中心的兩側

例5在平面直角坐標系中，已知點A（-4，2），B（-6，-4），以原點O為位似中心，位似比為，把△ABO縮小，則點A的對應點A′的坐標是（）

A.（-2，1）B.（-8，4）

C.（-8，4）或（8，-4）D.（-2，1）或（2，-1）

【錯解】選A

【析錯】位似中心在坐標原點，進行分類討論.若“同側”，則對應點的橫（縱）坐標的比就是位似比，若“異側”，則對應點的橫（縱）坐標的符號相反.選D.

五、相似三角形分類討論

例6如圖4，在△ABC中，∠C=90°，AC= 3cm,BC=4cm，動點P從點B出發以2cm/s的速度向點C移動，動點Q從點C出發以1cm/s的速度向點A移動，如果動點P、Q同時出發，要使△CPQ與△CBA相似，所需要的時間是多少秒？

圖4

【錯解】若△CPQ∽△CBA，

【析錯】△CPQ與△CBA相似，在沒有告訴對應點的情況下應該分兩種情況，一種是△CPQ∽△CBA，另外一種是△CPQ∽△CAB.

所以在應用相似三角形解決問題的時候我們要注意分類思想的應用.

同學們，剛才分析了圖形的相似這一章中易錯的一些問題.面對問題只要認真整理歸納、糾正并及時反思，我們的學習就一定會天天向上.

（作者單位：江蘇省常熟市周行學校）