借力課本習題拓展基本圖形

許　歡

借力課本習題拓展基本圖形

許歡

蘇科版《數學》九年級下冊第57頁的練習3：如圖，在矩形ABCD中，DE⊥AC，垂足為E.圖中有哪些三角形與△ABC相似？為什么？

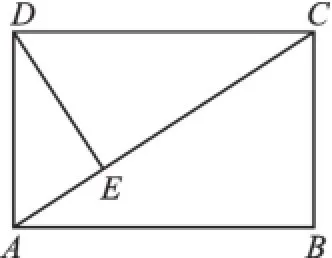
矩形被一條對角線分得的兩個三角形全等，而直角三角形斜邊上的高把原直角三角形分成兩個直角三角形，這兩個三角形都和原三角形相似.所以圖中△ADC、△ADE、△CDE與△ABC都相似.

上題中出現了一個基本圖形（見下面圖1）.其實在研究數學問題中，若能捕獲到一些基本圖形，則會縮短我們的思維路徑，提升解題效率.

圖1

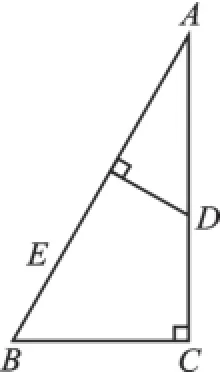
圖2

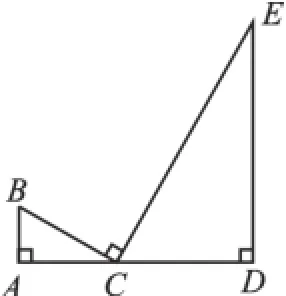
圖3

在相似三角形的學習中出現并整理過多種基本圖形，這里以“垂直型”為例：如圖1“雙垂直共角共邊型”（也稱“射影定理型”）；如圖2“雙垂直共角型”；如圖3“三垂直型”.

在2016年蘇州市中考試卷中就有類似考題能用這些基本圖型來解答.

例1如圖4，在平面直角坐標系中，已知點A、B的坐標分別為（8，0）、（0，23），C是AB的中點，過點C作y軸的垂線，垂足為D，動點P從點D出發，沿DC向點C勻速運動，過點P作x軸的垂線，垂足為E，連接BP、EC.當BP所在直線與EC所在直線第一次垂直時，點P的坐標為.

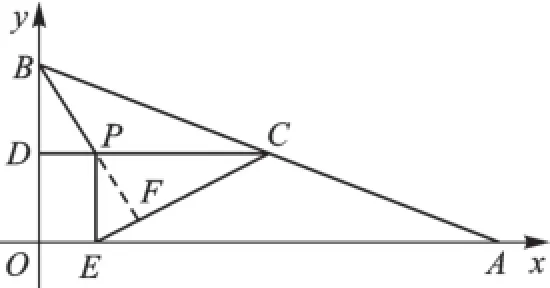
圖4

【解析】如圖4，當BP所在直線與EC所在直線第一次垂直時，即BP⊥EC，垂足為點F時，出現“雙垂直共角共邊型”，得△CPF∽△CEP，另外在BF、DC相交所形成的“8字型”中，有一對對頂角相等，一對直角相等，可得△CPF∽△BPD，進而有△CEP∽△BPD，可以列出有關DP、PE的比例式，再根據“坐標及平行線分線段成比例”即可得答案.求得點P的坐標為（1，）.

例2如圖5，在矩形ABCD中，AB=6cm，AD=8cm，點P從點B出發，沿對角線BD向點D勻速運動，速度為4cm/s，過點P作PQ⊥BD交BC于點Q，以PQ為一邊作正方形PQMN，使得點N落在射線PD上，點O從點D出發，沿DC向點C勻速運動，速度為3m/s，以O為圓心，0.8cm為半徑作⊙O，點P與點O同時出發，設它們的運動時間為t（單位：s）

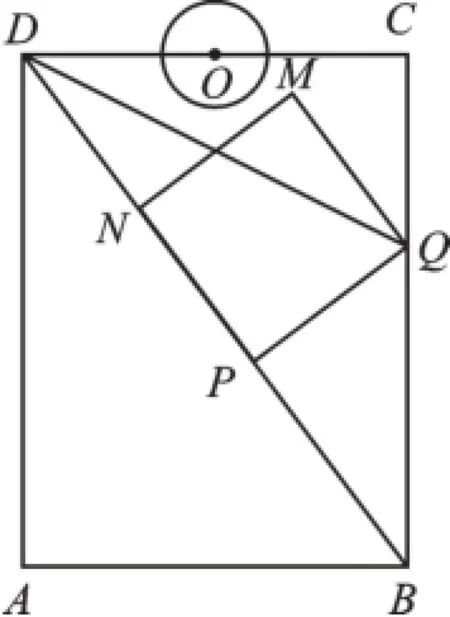
圖5

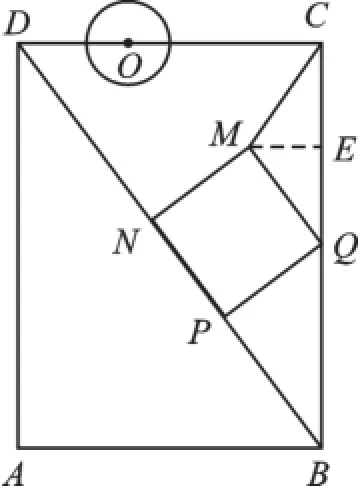
圖6

（1）如圖5，連接DQ，當DQ平分∠BDC時，t的值為；

（2）如圖6，連接CM，若△CMQ是以CQ為底的等腰三角形，求t的值.

【解析】（1）由正方形PQMN，可得QP⊥BD，結合△BCD，出現“雙垂直共角型”，可得△BPQ∽△BCD，從而求出PQ、BQ，再根據角平分線性質定理可得PQ=CQ.

（2）作ME⊥BC于點E（如圖6）.

△QEM和△BPQ之間出現類似“三垂直型”，即△QEM∽△BPQ，進而可得△QEM∽△BCD，再結合等腰三角形“三線合一”性質，即可得到答案.

掌握一些相似三角形的基本圖形，將它們與其他知識點充分結合，透過外形看清本質，一定能夠快速地獲取解決此類問題的思路與方法.

（作者單位：江蘇省常熟市實驗中學）

挑戰壓軸題

（本題由江蘇省常熟市孝友中學朱明芬提供）