無窮大的比較及應用

李海霞 聶東明

(安徽新華學院公共課教學部安徽合肥230088)

無窮大的比較及應用

李海霞 聶東明

(安徽新華學院公共課教學部安徽合肥230088)

利用無窮大的比較，討論了無窮大的比較在比較函數大小、計算極限、確定方程的根及判斷正項級數收斂性上的應用。

無窮大；無窮大的階；函數大小；極限；正項級數收斂性

無窮小的比較是極限理論及極限計算的重要工具，是高等數學中一個非常重要的知識點，所以關于無窮小的討論非常多[1-4]。仿照無窮小的比較，也可以給出無窮大的比較的概念[5]，并且無窮大的比較的應用也非常廣泛[6-11]。本文根據常見函數增大快慢速度，即無窮大的階，探討無窮大在比較函數大小、極限計算、方程的根及判斷正項級數收斂性等方面的應用。

1.無窮大的比較概念

定義1.1[5]設u(x)、v(x)是同一變化過程中的無窮大，且v(x)≠0，在這個變化過程中，

定理1.1[5]當n→∞,1nαn(α＞0),nβ(β＞0),an(a＞1),n!,nn是一個比一個更高階的無窮大。

將上述自然數n換成變量x，得到。

推論1.2當n→+∞,1nαx(α＞0),xβ(β＞0),ax(a＞1)是一個比一個更高階的無窮大。

（若α為非整數，可連續使用s次羅比達法則，使得α-s＜0為止，

根據以上定理和推論，介紹無窮大的比較的應用。

2.無窮大的比較在比較函數大小中的應用

利用推論1.2，很容易得到答案為C。而答案解析過程是利用羅比達法則求極限，結合極限的局部保號性得出答案。如比較f(x)和g(x)的大小，根據：

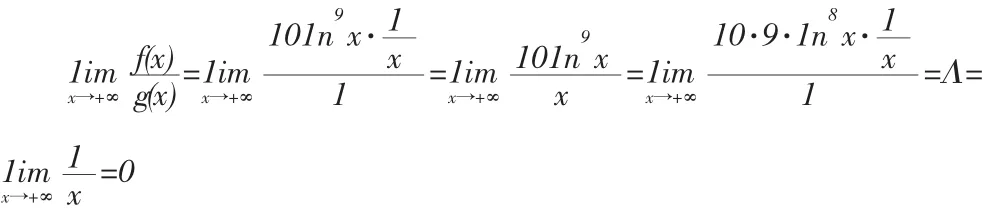
由極限局部保號性，f(x)＜g(x)；同理可得g(x)＜h(x)。

3.無窮大比較在極限計算中的應用

無窮大比較在極限計算中的應用，也有論文談及[5-10]，但主要是仿照等價無窮小代換，利用等價無窮大代換求極限。事實上，完全可以利用推論1.2來求極限。

例3.1[12]為正整數，λ＞0）。

解：相繼應用羅比達法則n次，得

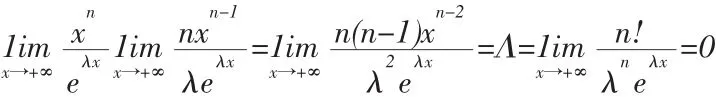
本題若利用eλx是xn的高階無窮大（λ＞0，所以eλ＞1），很容易得到結果為0。

4.無窮大的比較在判斷方程根中的應用

例4.1討論方程1nx=ax（其中a＞0）有幾個實根？

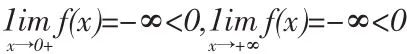
判斷方程實根存在性時，常利用零點定理，而題中a是一個大于0的參數，若要在區間（0.+∞）找到一個點使得函數f(x)取到正值，很難實現；另一方面，若利用函數1nx和冪函數xβ當x→+∞時增大的快慢速度，很容易判斷出結合極限的局部保號性，一定存在當x＞M時，f(x)恒為負值。那么方程1nx=ax即f(x)=0是否有根既實根的個數，就要觀察曲線y=f(x)是否穿過x軸，亦即f(x)的極大值在x軸上方或下方來決定。具體求解過程如上。

5.無窮大比較在判斷正項級數收斂性中的應用

此題利用了nβ是比1nn高階的無窮大量。

［1］陳大橋.等價無窮小代換在求極限中的常見應用及推廣[J].成都師范學院學報,2014,30(5):117-119.

［2］趙玉杰,李李.等價無窮小代換在求解含和差運算因子的極限中的運用[J].安慶師范學院學報(自然科學版),2013,19(4):204-206.

［3］李強.函數極限中等價無窮小的應用探討[J].銅仁學院學報,2009,11(3):142-144.

［4］凌壽銓.無窮小在極限及正項級數方面的應用[J].河北北方學院學報(自然科學版),2008,24(6):12-14.

［5］陳紀修，於崇華，金路.數學分析[M].高等教育出版社.

［6］侯麗.無窮小與無窮大的比較在廣義積分及級數的收斂中的應用探討[J].企業導報,2012（11）:229-50.

［7］侯麗.無窮大與無窮小的比較在極限運算中的應用[J].現代商貿工業，2012（15）.

［8］王梅英,陸偉東.無窮小與無窮大的階在極限運算及判級數斂散性中的應用[J].南京審計學院學報，2007,4（2）:73-76.

［9］孫衛衛,孫建英.等價無窮大在未定式計算中的應用[J].哈爾濱師范大學自然科學學報,2014,30(3):69-73.

［10］劉桂仙，劉慶升.求極限的等價無窮大代換[J].高等數學研究，2011,14（1），51-52.

［11］黃澤民.利用無窮大的比較判斷正項級數的斂散性[J].高等數學研究，1995（5）:9-10.

［12］同濟大學數學系編.高等數學[M].高等教育出版社.

Comparison of infinity and its application

LiHai-xiaNieDong-ming

(Department of Common Course,Anhui Xinhua UniversityAnhuiHefei230088)

On the basis of comparison of infinity,its application is discussed in comparison of function size,limit calculation,equation root and positive series convergence.

Infinity；Order of infinity；Function size；Limit；Positive series convergence.

O172

A

2095-7327（2016）-10-0131-02

安徽省高校自然科學研究重點項目（KJ2015A308）、安徽新華學院項目（2013xgg05,2014zr011,2015jy039）。

李海霞（1982—），女，漢族，河南南陽人，副教授。