一類部分和分解非對稱自回歸分布滯后模型的邊界檢驗

王敬勇

（1.南京審計大學會計學院，南京210029；2.華中科技大學經濟學院，武漢430074）

一類部分和分解非對稱自回歸分布滯后模型的邊界檢驗

王敬勇1,2

（1.南京審計大學會計學院，南京210029；2.華中科技大學經濟學院，武漢430074）

部分和分解形成的非對稱性機制表明了經濟變量的正向變化不同于負向變化，文章利用部分和分解構造的自回歸分布滯后模型，不僅可以處理時間序列的內生性與誤差的序列相關問題，還可以通過邊界檢驗方法，分析非對稱機制與非平穩性的聯合問題。中美兩國利率數據分析表明該模型應用的靈活性與可行性，并得到了美國利率傳導的短期動態非對稱性的結論。

部分和分解；非對稱性；邊界檢驗；自回歸分布滯后模型

0　引言

非線性模型表明經濟變量的正向變動與負向變動，偏離了長期均衡路徑，那么向長期均衡路徑回復的速度也不同，即經濟擴張過程和經濟衰退過程導致的經濟變量對長期均衡路徑的偏離的回復過程是非對稱的，這正是非線性機制與非平穩性的聯合問題。目前的研究一般是從以下三種非線性機制模型展開的：Balkeand Fomby（1997）的三機制閾值ECM模型，Kapetanios et al（2006）的平滑轉制ECM模型，以及Psaradakisetal（2004）的馬爾科夫ECM模型，機制轉換變量以及機制轉換函數的選擇決定了三種模型處理上的不同。除了這三種非線性機制協整模型外，Schorderet（2001）提出了一種新的非對稱機制模型，其在研究失業與產出的非對稱關系時，把產出變量分解為正向與負向變化的部分和過程，并依據這種分段線性設定，發現衰退過程引起的失業率上升大于擴張過程導致的失業率下降。進一步Schorderet（2003）把這種非對稱機制引入協整檢驗，如果經濟變量的正向變化部分與負向變化部分構成的線性組合是平穩的，則表明經濟變量是“非對稱協整”。部分和分解的非對稱協整模型的基本思想是，經濟變量的正向變化不同于負向變化，從而產生了非對稱性。但Schorderet（2003）的模型受到了解釋變量的內生性與誤差的序列相關問題的約束。借鑒內生性問題處理方法，引入解釋變量以及被解釋變量的滯后結構，構建部分和分解的自回歸分布滯后誤差修正模型，此種處理方法即降低了內生性程度，又解決了誤差序列相關問題，且可以同時模擬長期和短期非對稱行為。對于非對稱自回歸分布滯后誤差修正模型的非平穩性與非對稱問題，可以使用標準的0LS方法進行估計，并借鑒Pesaran etal（2001）邊界檢驗方法，構造非平穩性與非對稱性的聯合F統計量。本文利用中美兩國的利率數據，實際分析說明該模型應用的有效性。

1　部分和分解的非對稱協整模型

時間序列可以分解為初值、負向變化與正向變化的累積和，因此一個隨機游走過程可以分解為帶漂移項的兩個隨機游走過程，檢驗由分解產生的多變量的線性組合，如果該現象組合是平穩的，則產生一種新的協整。考慮時間序列xt分解為：

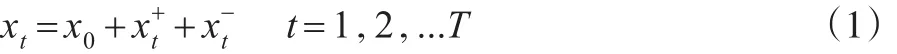
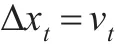
2　非對稱自回歸分布滯后模型的構建

在應用（3）式的非對稱協整模型中，解釋變量內生性，以及誤差序列相關，會顯著地影響估計量與檢驗統計量的小樣本性質。面對這些問題，可以借鑒動態0LS解決內生性問題的思路，在（3）式中引入解釋變量與被解釋變量的動態性，把靜態回歸模型轉變為動態回歸模型，不僅可以有效降低內生性程度，且動態回歸模型在模擬長期和短期非對稱行為時，參數更具有靈活性，同時也可以利用合適的動態結構解決誤差序列相關問題。在（3）式中引入解釋變量與被解釋變量的滯后結構，則（3）式變換為非對稱自回歸分布滯后模型：

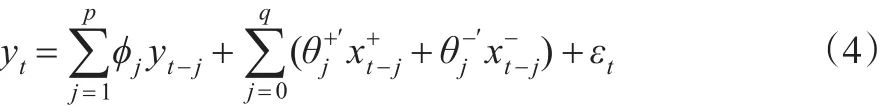
其中，xt是k×1向量，?j是自回歸參數，是分布滯后參數，εt是零均值，常方差分布。把（4）式變換為誤差修正模型：

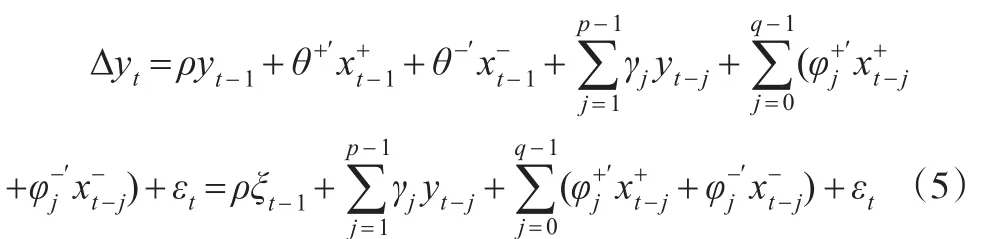
vt是獨立同分布，零均值的平穩過程，方差是k×k的正定協方差矩陣。由于（5）式中回歸變量△xt與εt相關，則可以把εt表示為vt的函數：

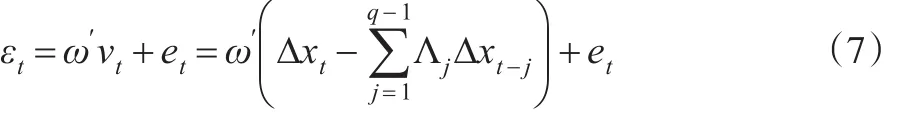
其中，et與vt不相關，把（6）和（7）式代入（5）式，可以得到修正的非線性誤差修正模型：

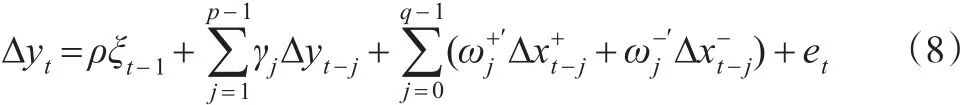
該模型也可以稱為非線性自回歸分布滯后誤差修正模型，（8）式不僅修正了內生性問題，也可以通過滯后結構的選擇解決誤差序列相關問題。（8）式結合了內生性修正與動態修正模型優點。此外，利用這種轉換方法，（8）式所有參數都可以使用標準的0LS方法進行估計與假設檢驗。根據Pesaran and Shin（1998）的定理3.1和3.2，如果xt是由（6）式生成的非平穩變量，et是獨立同分布且與vt不相關，則（8）式中短期動態參數0LS估計量具有T的收斂速度，并具有漸近正態性；而長期參數的0LS估計量具有T的收斂速度，具有漸近混合正態分布。

3　聯合F統計量的邊界檢驗

按照Pesaran etal（2001）邊界檢驗方法，檢驗（8）式的協整關系，可以構造ρ=0的原假設以及ρ＜0的備擇假設，并通過t統計量進行假設檢驗，如果接受了ρ=0，則表明yt與不具有協整關系。

為了檢驗分布滯后誤差修正模型中是否存在部分和分解的非對稱效應，需要分別檢驗長期對稱系數θ+、θ-，與短期對稱系數ω+、ω-是否相等，檢驗長期與短期動態非對稱性的原假設和備擇假設分別為H0:θ+=θ-、H1:θ+≠θ-；H0:ω+=ω-、H1:ω+≠ω-。

在非對稱檢驗時，施加不同的約束可以使模型更具靈活性，因此，非對稱模型又可以設定以下四類，

一是短期與長期非對稱檢驗模型，也可以稱為無約束模型：

該模型對于短期非對稱檢驗ω+=ω-時，可以使用Wald統計量，而長期非對稱檢驗θ+=θ-即可以使用Wald統計量，也可以構造ρ=θ+=θ-=0的非平穩性與非對稱性聯合假設檢驗F統計量：

RSSr是約束模型的殘差平方和，RSSu是非約束模型的殘差平方和，T是樣本容量，k是回歸變量的數量（包括常數項），q是施加約束的數量。

第二種模型是短期非對稱性與長期對稱性，簡稱模型2，其形式如下：

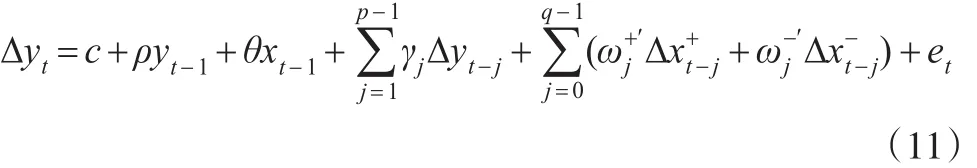
（11）式可以分別使用t和Wald統計量分別檢驗協整關系與短期非對稱性。

第三種模型是短期對稱性與長期非對稱性，簡稱模型3，其形式如下：

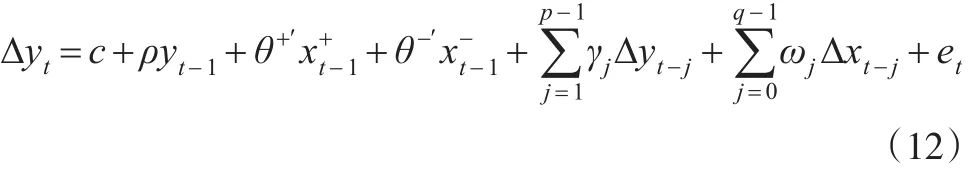
（12）式可以分別使用t和Wald統計量檢驗協整關系與長期非對稱性，也可以使用聯合假設檢驗F統計量，

第四種模型是短期對稱性與長期對稱性，簡稱模型4，其形式如下：

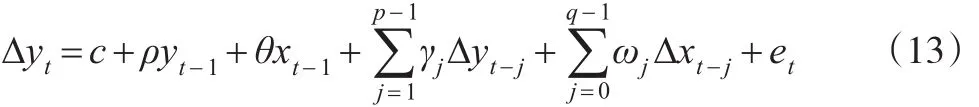
（13）式是線性模型，只需要檢驗協整關系。在這四種模型下，利用Pesaran etal.（2001）一文中的t統計量與聯合F檢驗統計量的臨界值邊界，可以對非平穩性與非對稱性進行推斷。

4　實證分析

本文擬使用中美兩國的利率數據，分析美國貨幣政策的國際傳導過程中，利率渠道的非對稱性。中美兩國的利率數據分別為1996年1月至2013年12月銀行間7天加權平均同業拆借利率，數據來源中國人民銀行；美國的數據采用3個月聯邦基準有效利率，數據來源www.econstats. com。為了降低異方差的影響，本文的數據全部取自然對數，其中ru表示美國聯邦基準利率，rc表示中國拆借利率。

對名義利率與通脹率序列平穩性進行檢驗，結果表明都為非平穩序列，但其一階差分是平穩的。為了初步說明兩國利率之間的關系，本文考察了兩國利率的因果關系，檢驗結果如表1所示。

表1　兩國利率的因果檢驗

美國利率政策變化是中國利率變動的格蘭杰原因，反之不成立，表明美國通過調整基準利率，會傳導到中國，從而引起中國利率政策作出相應的調整，而中國利率政策的變化目前還不能引起美國利率的調整。進一步，我們通過非對稱自回歸分布滯后模型，分析美國利率政策變化對中國利率影響的非對稱性。基于非對稱ARDL-ECM模型的邊界檢驗方法，采用從一般到特殊的建模方法，根據Shin，Yu and Greenwood-Nimmo（2011）對滯后期的經驗設定，月度數據選擇最大的滯后期為（p,q）=（12,12），使用序貫0LS方法對模型估計，最終再刪除不顯著的滯后期變量，估計與檢驗結果如表2所示。自回歸分布滯后模型首先要檢驗兩國利率是否存在長期均衡關系，表2中的模型4、模型3的Fpss統計量均沒有達到統計量上界臨界值5.73，表明這兩種模型可能設置錯誤。進一步觀察模型1與模型2，這兩種模型的Fpss統計量均超過統計量上界臨界值，表明兩國利率存在著長期的均衡關系，但由于模型1中長期非對稱項系數不顯著，且長期非對稱檢驗Wald統計量也不顯著，表明美國聯邦基準利率對中國銀行間拆借利率的傳導機制只存在短期的非對稱效應。模型2中，短期內美國聯邦基準利率的正向變化與中國銀行間拆借利率成反比，負向變化與中國銀行間拆借利率成正比，且存在著滯后效應。一方面反映了中國短期銀行間拆借利率并不與美國聯邦基準利率變化而同步調整，存在著滯后性；另一方面，短期非對稱性表明，中國短期利率變動面對美國聯邦基準利率政策調整的正向沖擊與負向沖擊是不對稱的。兩國間利率的長期均衡關系與美國利率政策在短期內的影響，共同決定了中國短期利率政策的變動。

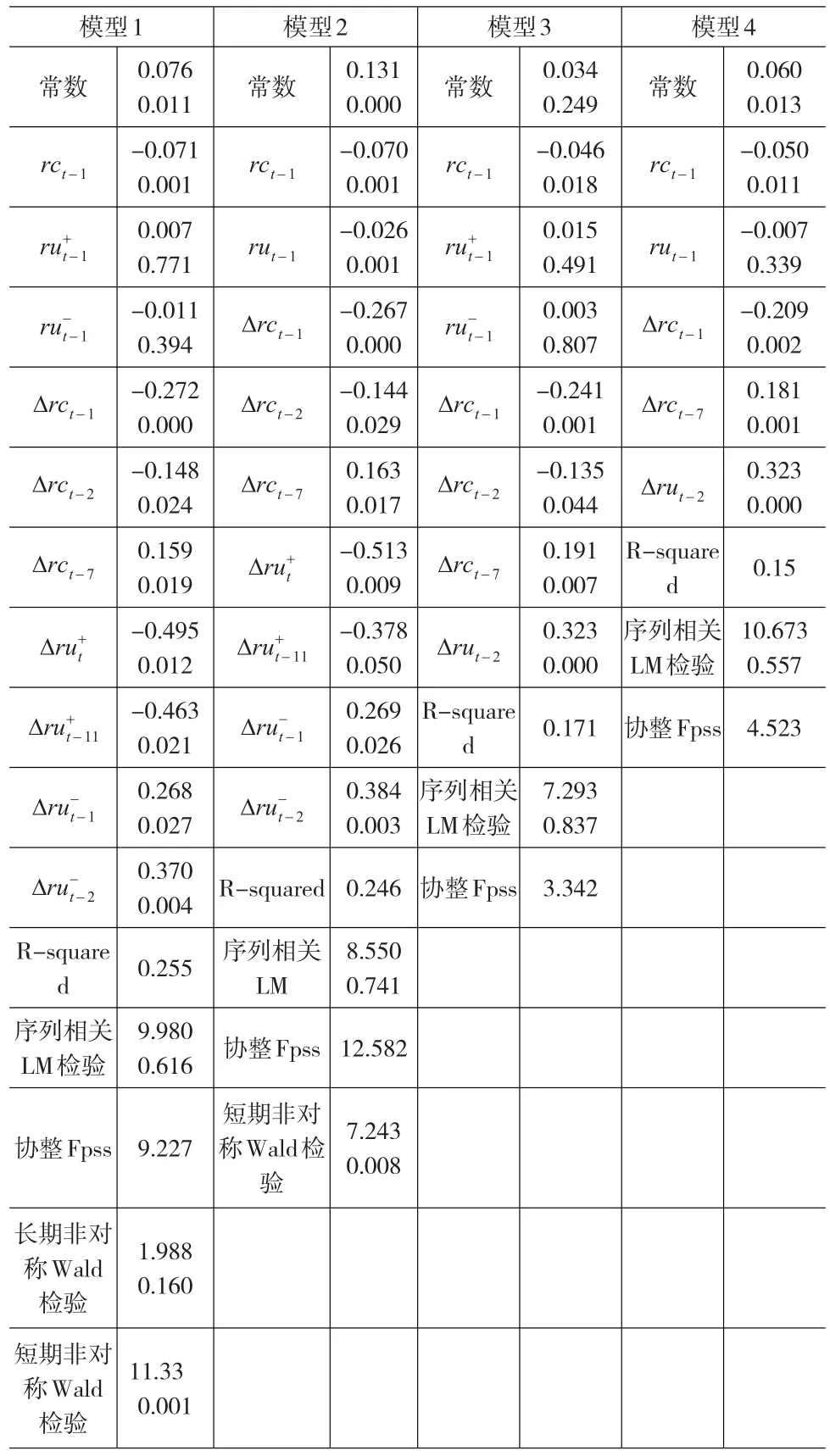
表2　非對稱自回歸分布滯后模型估計與檢驗

5　結論

部分和分解的非對稱模型的基本目的是說明經濟變量的正向變化與負向變化對系統影響的非對稱性，該模型聯合了非平穩性與非對稱性問題，通過構建非對稱自回歸分布滯后模型，不僅考慮了長期非對稱性也可以分析短期動態的非對稱性，同時還可以處理時間序列估計中的內生性與誤差序列相關問題。借鑒Pesaran etal（2001）邊界檢驗方法，構建聯合F檢驗統計量，可以同時檢驗長期的均衡關系與非對稱機制。本文利用中美兩國利率數據，分析了美國利率傳導的短期動態非對稱性，說明了該模型應用的靈活性與可行性。

[1]Balke N S，Fomby TB.Threshold Cointegration[J].International Eco?nomic Review,1997，38(3).

[2]Kapetanios G,Shin Y，Snell A.Testing for Cointegration in Nonlinear Smooth Transition Error Correction Models[J].Econometric Theory, 2006，22(2).

[3]Psaradakis Z,Sola M，Spagnolo F.On Markov Error-Correction Mod?elsWith an Application to Stock Prices and Dividends[J].Journal of Applied Econometrics,2004，19(1).

[4]Shin Y,Yu B,Greenwood-Nimmo M.Modelling Asymmetric Cointe?gration and Dynamic Multipliers in an ARDL Framework[J].Ssrn Electonic Journal,2013.

[5]Pesaran M H,Shin Y,Smith R J.Bounds Testing Approaches to the Analysis of Level Relationships[J].Journal of Applied Econometrics, 2001，16(3).

[6]Pesaran M H,Shin Y.An Autoregressive Distributed Lag Modelling Approach to Cointegration Analysis[J].Econometrics and Economic Theory:The Ragnar Frisch Centennial Symposium,ed.S.Strom,1998.

（責任編輯/易永生）

021；F224

A

1002-6487（2016）19-0013-03

王敬勇（1978—），男，安徽淮北人，博士后，副教授，研究方向：計量經濟學方法。