基于區間Vague集的人-崗動態匹配模型

鄒樹梁，武良鵬

（南華大學經濟與管理學院，湖南衡陽421001）

基于區間Vague集的人-崗動態匹配模型

鄒樹梁，武良鵬

（南華大學經濟與管理學院，湖南衡陽421001）

針對現實生活中人崗匹配問題，文章提出一種新的決策方法。該方法首先引用區間Vague集來描述人崗匹配中的模糊性，通過自下而上的逆向指標體系構建方法，構建了人崗匹配的評價指標體系。為了體現出人崗匹配的動態性，定義了區間Vague集的預測方法，運用新的方法對屬性權重進行賦權。在此基礎上，利用前景理論對人崗匹配度進行測算，并在時間維度上進行縱向集成。

人崗匹配；區間Vague集；動態性；預測

0　引言

隨著時間的推移，現在已經進入了以人才資本為依托的經濟發展時代，人力資源已然成為現代企業發展的第一資源[1]。人和崗位是人力資源中的兩大要素，由此員工與崗位是否合理匹配成為人力資源管理中的熱點問題[2]。國外很多學者對人崗匹配模型進行過研究，Roth[3]等人較早的根據醫院招實習生的情況，給出了H-R匹配算法，為后來的研究提供了方向性的指導；Motowidlo[4]等人對影響人崗匹配因素做出了多方面研究，并對周邊績效和任務績效做出了區分；Lin[5]通過建立混合整數規劃模型，來解決畢業生與企業間的雙邊匹配問題；Jung[6]等人在對食品行業的研究基礎上，得出員工職業素質對人崗匹配有著重要影響。同樣我國學者對人崗匹配也做出了大量研究，張莉莉[7]等人突破了人崗匹配中人員能力具有同質性的假設，提出了構建基于優勢的四位一體的人崗匹配模型，體現出了以人為本的優點；王慶[8]等人利用BP神經網絡對人崗匹配度進行測算，使得人崗匹配變的更加智能化；陳希[9]等人提出一種兩階段測評與選擇方法，對人崗匹配中不同形式的滿意度評價信息進行了考慮。

但已有研究中不同學者對人崗匹配評價指標體系持不同的看法，沒有達成一致；同時大多為靜態人崗匹配研究，對動態的人崗匹配較少提及；而且隨著人們考慮問題的不確定性和思維的模糊性，將模糊數運用到人崗匹配中已經是不可避免，但又存在一般模糊數對問題的模糊性刻畫粗糙的問題。由此，針對這些問題，本文首先利用自下而上的逆向指標體系構建方法構建人崗匹配的評價指標體系，同時利用區間Vague集來刻畫問題的模糊性，并定義了基于GM(1.1)模型的區間Vague集預測方法，從而對人崗匹配進行動態匹配。

1　研究準備

1.1區間Vague集的基本知識

定義1[10]：Vague集：設論域U為非空有限集合，x為U上元素。U上一Vague集A由隸屬度函數tA(x)和非隸屬度fA(x)表示。隸屬度函數tA(x):U→[0，1]，表示的是支持x∈A的證據的隸屬度下界；非隸屬度函數fA(x):U→[0，1]，表示的是反對x∈A的證據的隸屬度下界。通常tA(x)+fA(x)＜1，則稱πA(x)=1-tA(x)-fA(x)為x相對于Vague集A的猶豫度，表示對A未知信息的一種度量，則x對于A的表示應具有三維信息，即(tA(x)，fA(x)，πA(x))。一般情況下將Vague集簡記為(tA(x)，fA(x))。當πA(x)為0時，Vague集退化為一般的FUZZY集。稱閉區間[tA(x)，1-fA(x)]為Vague集A在x點的Vague值。

定義2[11]：區間Vague集：稱Vague集為區間Vague集，其中=[a，b]?[0，1]，[0，1]，且b+d≤1。區間Vague集分別由區間隸屬度和區間非隸屬度組成，一般情況下簡記為V=([a，b]，[c，d])。

1.2問題描述

將所有備選方案形成的方案集合（Alternative set），記為A={a1，a2，…，am}，ai表示第i個方案，i=1，2，…，m；設指標集（Criteria set），記為表示第j個指標，j=1，2，…，n，屬性j的權重為；時間序列為，tk為k時刻，k=1，2，…，o；為備選方案ai針對屬性cj在時間段tk下的評價值；為決策者針對屬性j的期望水平，由于區間Vague集分別從區間隸屬度、區間非隸屬度和區間猶豫度三方面來表示決策者的偏好信息，能夠比一般模糊數更加細膩的描述問題的不確定性，因此的取值為區間Vague集。最后通過這些信息，對備選方案進行評價，找出評價值最高的方案，其示意圖如圖1。

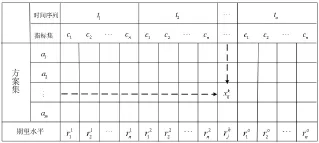
圖1　問題描述示意圖

2　人-崗匹配指標體系建立

對人崗匹配指標體系的構建，大多采用的是傳統自上而下的指標體系構建思路，這種思路通過直觀的抽象分析，從概括到具體的正向逐層構建指標。一般思路為從總目標出發，分解細化為子目標，通過層層分析，最后形成可以量化的指標集，但這種方法主觀性大，構建出的評價指標體系的正確性無法得到驗證。隨著人們對人崗匹配研究深入，積累了大量的評價信息。基于此，本文將評價信息搜集起來，并試圖通過信息之間的相似性，將其進行聚類，從而實現自下而上的指標體系的構建。則指標體系建立的步驟如下：

(1)對現有分散的指標體系進行挖掘與處理。不同的國家對人崗匹配的評價可能會存在不同的指標體系，由此，本文挖掘的信息均來自國內，不涉及國外信息。在中國知網和萬方數據庫中檢索“人崗匹配”、“人崗匹配指標體系”、“人崗匹配度測算指標體系”等關鍵詞，并選取被引用次數“10”以上的相關論文共96篇，人工整理合并出指標23項，分別為身體健康狀況、外在形象、業務水平、學習能力、管理能力、創新能力、忠誠度、責任感、業績、獎勵、洞察能力、團隊合作能力、敬業精神、經驗、知識技能、薪酬、心理狀況、學歷、決斷能力、意志力、執行力、風險意識、傾聽能力。

(2)邀請專家對這23項名詞進行兩兩比較，并判斷出兩者之間的相似性，由于篇幅關系，本文只列出了部分相似性矩陣如表1。

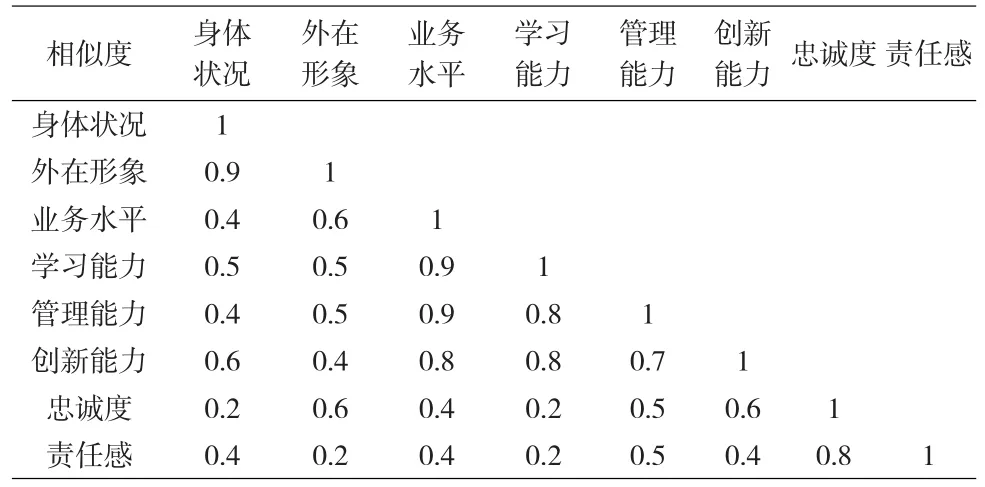
表1　基本指標元素相似度矩陣

(3)對基本指標元素進行相似度聚類。

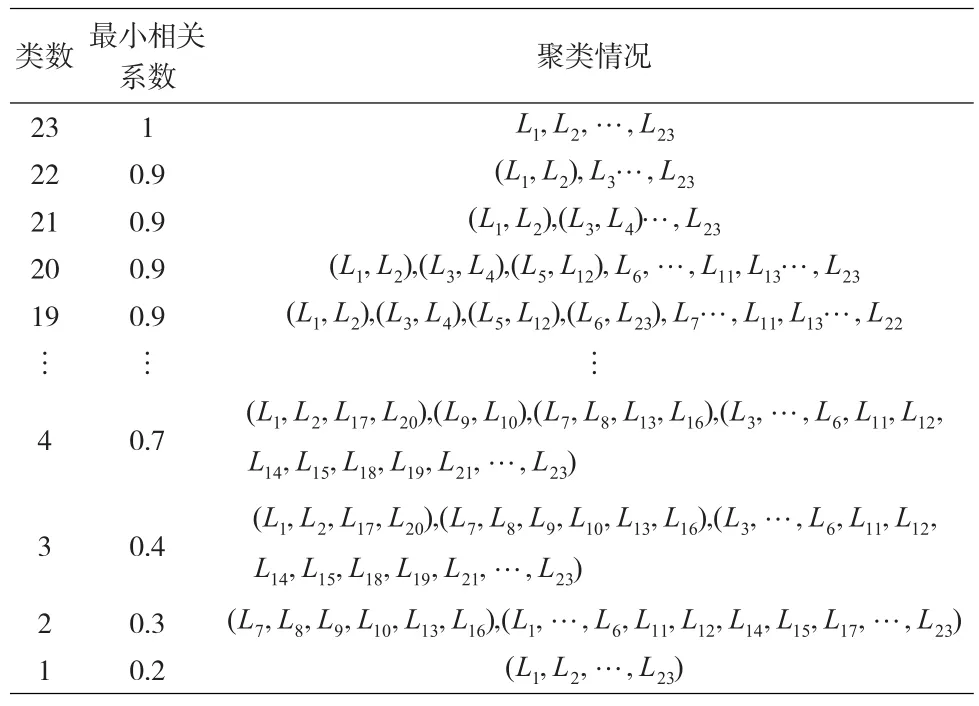
表2　聚類過程表

從表2可以看出，類數從4變為3時，分類內部最小相關系數由0.7減到0.4，下降幅度過大，且分為4類時最小相關系數0.7大于一般人們設定的相似度閥值0.6，由此，將基本指標元素聚類為4類：=身心素質；c2=(L9，L10)=獲得過的榮譽；c3=(L7，L8，L13，L16)=道德素質；L23)=能力素養。

3　人-崗動態匹配模型

3.1基于GM(1.1)模型的區間Vague集預測模型

傳統的人崗匹配方法注重在某一個特定的時刻下，候選人之間能力水平的橫向一次性比較，忽略了候選人自身能力的縱向發展，對候選人未來能力和崗位未來期望水平的預測研究較少。為了體現出匹配動態性，首先對候選人能力和崗位期望水平進行預測，本文提出一種基于GM (1.1)模型的區間Vague集預測模型。

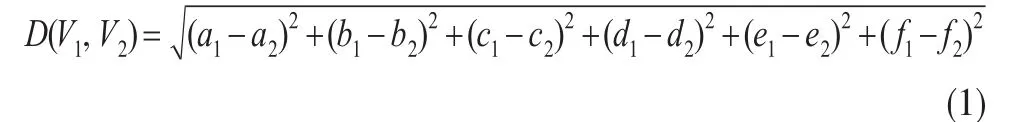
其中e1，e2為猶豫度下限；f1，f2為猶豫度的上限。可以證明距離公式(1)是完備的。

②當D(V1，V2)=0時，則a1-a2=0，b1-b2=0，c1-c2=0，d1-d2=0，e1-e2=0，f1-f2=0，則V1=V2；相反，當V1=V2時，a1=a2，b1=b2，c1=c2，d1=d2，e1=e2， f1=f2，則，從而D(V1，V2)=0?V1=V2；

③D(V1，V2)=；則D(V1，V2)=D(V2，V1)；

④若V1，V2，V3為任意三個區間Vague集，且V1?V2?V3，則D(V1，V3)≥D(V2，V3)；這是因為當V1?V2?V3時，a1≤a2≤a3，b1≤b2≤b3，c1≥c2≥c3，d1≥d2≥d3，e1≤e2≤e3，f1≥f2≥f3，則同理D(V1，V3)≥D(V2，V3)。

綜上證明，距離公式(1)是完備的。

現有研究中，對區間Vague集特性表征最多的概念是得分函數和精確函數，因此自然的我們會想到利用得分函數和精確函數對區間Vague集進行預測，但僅轉化得分函數和精確函數是丟失大量信息的，由此本文引入另兩個函數來對區間Vague進行描述：

定義4：稱T=b+c-a-d為區間Vague集V=([a，b]，[c，d])的隸屬不確定函數。

定義5：稱G=b+d-a-c為區間Vague集V=([a，b]，[c，d])的猶豫不確定函數。

可以證明-1≤T≤1，0≤G≤1，證明略。

在對不確定的預測上，通常根據灰度不減原理，認為不確定性在經過一系列運算后，其不確定性是不可能減少的[12]，由此取預測值G2，…，Gn}；或者認為不確定到確定需要信息不斷的補充，由此在沒有額外信息補充的條件下，不確定度趨向于均值[13]，即而無論是取最大值還是取均值，其隸屬不確定和猶豫不確定均分別屬于[-1，1]和[0，1]，本文的思想是將T和G視為預測模型的參數，運用精度最大化模型確定最優的T和G。

假設預測原序列為[V1，V2，…，Vn]，其中Vi表示排在第i的區間Vague集，且Vi=([ai，bi]，[ci，di])，Vi的猶豫度記為[ei，fi]；而預測之后的序列記為，其中表示預測后排在第i的區間Vague集的猶豫度記為需要說明的是，在預測之前，Vi并不是確切的實數，而是關于T和G的不確定表達式。首先對原序列對應的得分函數序列和精確函數序列[H1，H2，…，Hn]利用GM(1.1)模型進行預測，以得分函數序列為例：

其還原值為：

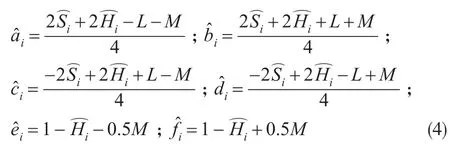
式(4)中L和M未知，為了求出L和M的值，根據距離式(1)，與原序列距離越近，則誤差越小，由此建立如下模型。

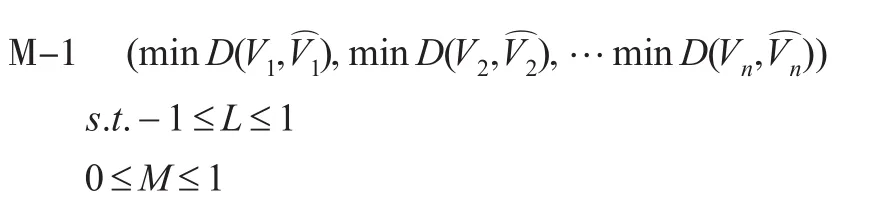
由于各對序之間不存在偏好，將模型1改寫為如下形式：

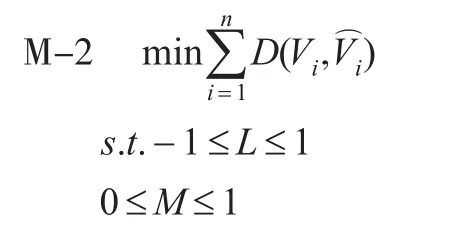
求解模型2可解出最優參數L和M，之后代入式(4)求出預測值。

從而根據式(1)至式(4)以及模型2，可預測出未來幾年候選人能力和崗位期望水平。

3.2屬性權重與時間節點權重的確定

3.2.1屬性權重的確定

屬性權重是對屬性在決策中作用和地位差異的描述，本文認為，影響權重差異主要有每個方案的各個單屬性價值的可靠程度、各個屬性在決策過程中所起的作用程度、決策者對各個屬性的偏好程度等3個方面，由此本文從這三個方面綜合考慮，為屬性賦權。

(1)屬性的可靠度。每個方案的各個單屬性價值的可靠程度影響著屬性權重的差異，單屬性價值指的是某方案在單個屬性上的價值水平，這種水平是由決策者給出，最直觀的表現就是屬性值，針對區間Vague集時，本文認為猶豫不確定越小，提供的信息就越充分，屬性值就越精確，從而屬性的可靠度越高，由此

(2)屬性的作用度。屬性的作用度是根據客觀數據所定，不受主觀影響，不同方案下同一個屬性差異越大，則屬性提供的信息越多，對決策起到的作用就越大；相反，屬性值的差異越小，對決策起到的作用也就越小，本文利用距離來衡量決策屬性間的差異。

根據公式(1)，k時刻同一屬性下任意兩個區間Vague集的距離為，則總離差為建立離差最大化模型。

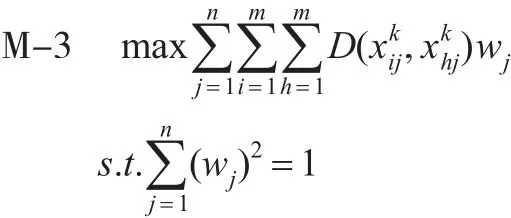
求解模型3，建立拉格朗日函數，L(wj，λ)=；分別對函數求偏導可得

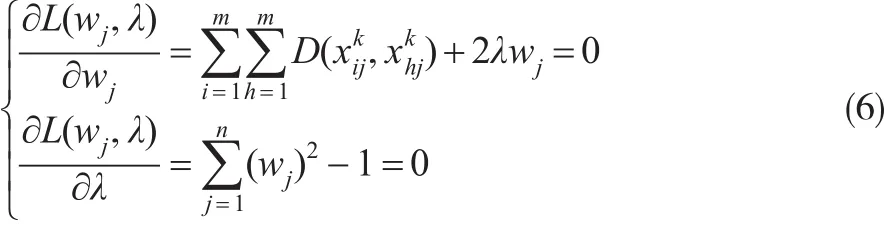
解式(6)可得

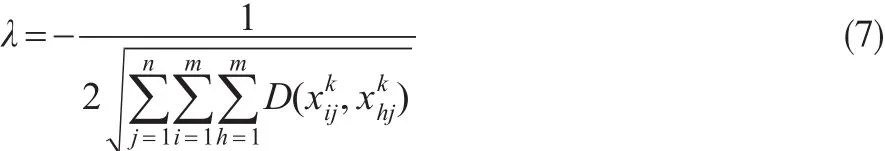
將式(7)代入式(6)，并歸一化處理可得

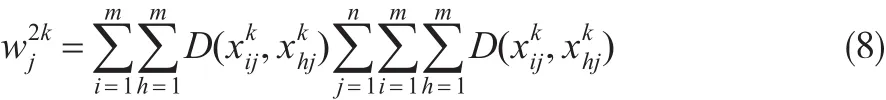
(3)決策者的對屬性的主觀偏好。如果屬性的權重不考慮決策者對屬性的影響，那么權重可能會與實際權重產生很大的反差。現實生活中決策者的知識水平、決策經驗都會影響到屬性的權重，將決策者對屬性的重視程度考慮到對權重的賦權里面，能使權重與實際權重更加接近，令決策者給出的主觀權重為

城市軌道交通的運營模式正在發生變化，新興模式在不斷誕生之中。未來一種可預見的模式是：運營業主無車輛所有權、僅有使用權，業主制定車輛RAMS(可靠性、可用性、可維護性和安全性)指標體系給予系統保證，城市軌道交通車輛制造商則提供長達數十年的車輛租賃服務。這一新興范式使得種種維修集約范式不復存在，而被旅客乘用綜合服務成本所替代。

3.2.2時間節點權重的確定

不同的決策者在對時間序列進行集成時，擁有不同的心理狀態，有的決策者比較看重過去的數據，有的決策者比較看重未來數據，也有決策者對當前數據比較看重，為了體現出決策者不同的心理狀態，本文應用Yager等人提供的一種模糊語言量化的方法[14]。

其中u為預測年數，β為模糊語言變量，一般取值有0、0.1、0.5、1、2、10和1000，對應取值的含義分別為非常看重過去、很看重過去、一般看重過去、同等對待、一般看重未來、很看重未來、非常看重未來，由此可以根據不同的β值來確定不同決策者對時間賦權。

3.3人-崗動態匹配評價模型

根據前景理論可知，在進行人崗匹配評價時，決策者會將候選人與參照物進行比較，這個參照物通常是事先定好的對崗位的期望水平要求。決策者會感覺到當候選人未超過期望水平時帶來的感受比超過期望水平時來的強烈，這是由于人是“有限理性”造成的。現代人力資源管理中的人崗匹配面臨的主要問題有兩方面，一是應聘崗位的候選人水平符合崗位基本要求，但離崗位期望要求水平太遠，導致小材大用；另一種就是遠超過崗位期望要求水平，導致大材小用。為了避免這兩種情況的出現，應該使得候選人水平盡量接近期望水平，由此做出定義：當候選人評價水平小于參考點，離崗位期望水平越遠則人崗匹配度越低；當候選人評價水平大于參考點，且與崗位期望水平的距離在一定范圍內時，離崗位期望水平越遠則人崗匹配度越高；當候選人評價水平大于參照點，且與崗位期望水平的距離超過一定范圍內時，就出現“大材小用”現象，由此人崗匹配度為0。

定義6[11]：假設任意兩個區間Vague集為V1，V2，則兩者大小比較規則如下：

當S1＞S2時，V1＞V2；S1＜S2時，V1＜V2；

當S1=S2時，若H1＞H2，則V1＞V2；若H1＜H2，則V1＜V2；

當S1=S2且H1=H2時，若T1＞T2，則V1＜V2；若T1＜T2，則V1＞V2；

當S1=S2、H1=H2、T1=T2時，若G1＞G2，則V1＜V2；若G1＜G2，則V1＞V2；若G1=G2，則V1=V2。

則對前景理論的方法進行改進并利用定義6得出候選人i在k時刻關于屬性j的匹配度為

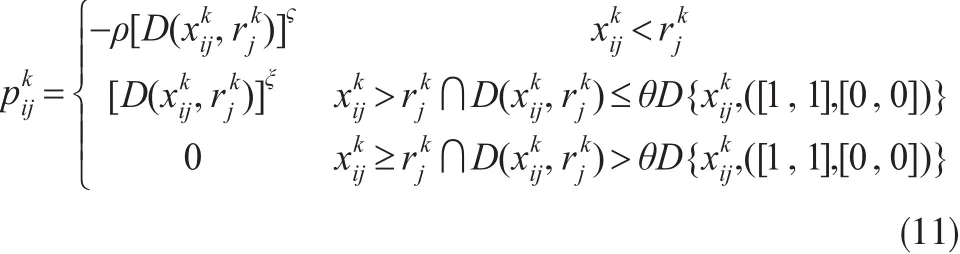
其中參數?和ξ反映了函數的凹凸程度，?和ξ的取值均大于0小于1，且取值越小敏感程度越低，決策者越趨于保守；ρ表示決策者風險厭惡程度，通常ρ＞1，且取值越大，對損失的規避程度越大；θ表示出現“大材小用”時的界點參數，0＜θ≤1，取值越大，界點越靠近最理想水平。

將候選人i在屬性上橫向集成后再從時間序列上縱向集成為最終匹配度為

pi越大，則人崗最終匹配度越大，候選人i則與崗位越適合。

綜上，本文提出算法步驟為

①根據自下而上的方式，建立人崗匹配評價指標體系；

②根據3.1節提出的方法，預測出候選人后u年的能力水平和崗位后u年的期望水平要求；

③根據式(7)至式(10)，分別確定屬性的權系數和時間權系數；

④根據定義6將評價水平與崗位期望水平進行比較，并利用前景理論計算候選人i在k時刻關于屬性j的匹配度；

⑤利用式(12)計算最終匹配度，并選出匹配度最高的候選人擔任該崗位。

4　結論

本文針對現實生活中的人崗匹配問題，提出了一種決策方法。該方法利用聚類的思想建立了人崗匹配評價指標體系，并利用區間Vague集對問題進行描述，能更好的體現問題的模糊性。同時提出了基于GM(1.1)模型的區間Vague集預測方法，體現了人崗匹配的動態性，拓寬了傳統屬性賦權的維度，使得屬性賦權更加完整。在此基礎上，對現有前景理論的方法進行改進，使得人崗匹配度測算時避免“小材大用”和“大材小用”的情況發生。

[1]袁有明.人力資源管理中的人崗匹配問題[J].市場周刊(理論研究), 2008,（9）.

[2]張志宇,呂明麗,李從東.基于BP神經網絡的人崗匹配測評模型的研究[J].天津大學學報(社會科學版),2010,（5）.

[3]Roth A E.The Evolution of the Labor Market for Medical Interns and Residents:A Case Study in Game Theory[J].The Journal of Political Economy,1984.

[4]Motowidlo S J,Van Scoter J R.Evidence That Task Performance Should Be Distinguished From Contextual Performance[J].Journal of Applied Psychology,1994,79(4).

[5]Hung-Tso Lin.A Job Placement Intervention Using Fuzzy Approach for Two-Way Choice.[J].ExpertSyst.Appl.,2009,（36）.

[6]Jung HYS,Namkung Y,Yoon HYH.The Effects of Employees'Busi?ness Ethical Value on Person-Organization Fitand Turnover Intent in The Foodservice Industry[J].International Journal of Hospitality Man?agement,2010,29(3).

[7]張莉莉,趙希男,臧義勇.基于優勢結構識別的人力資本四位一體匹配方法[J].系統工程理論與實踐,2013,（8）.

[8]王慶,劉琨,張志超.基于BP神經網絡的知識員工—崗位匹配測評研究[J].科技管理研究,2009，（10）.

[9]陳希,樊治平.組織中員工與崗位匹配的兩階段測評與選擇方法[J].東北大學學報(自然科學版),2009,(9).

[10]Gau W L,Buehrer D J.Vague Sets[J].IEEE Transactions on Sys?tems,Man,and Cybernetics,1993,23(2).

[11]Wang Z,Li KW,WangW.An Approach to Multiattribute Decision Making With Interval-Valued Intuitionistic Fuzzy Assessments and IncompleteWeights[J].Information Sciences,2009.

[12]李鵬,劉思峰,朱建軍.基于直覺模糊數的GM(1,1)預測模型[J].控制與決策,2013,（10）.

[13]袁潮清,劉思峰,張可.基于發展趨勢和認知程度的區間灰數預測[J].控制與決策,2011,（2）.

[14]劉斌,劉思峰,翟振杰,黨耀國.GM(1,1)模型時間響應函數的最優化[J].中國管理科學,2003,（4）.

（責任編輯/易永生）

C934

A

1002-6487（2016）19-0037-05

高等學校博士學科點專項科研基金(20134324110001)；中國博士后科學基金資助項目(2013M542123)

鄒樹梁（1956—），男，江西安福人，教授，博士生導師，研究方向：決策分析。