探索新公式

□徐永華

探索新公式

□徐永華

小朋友，我們已經知道兩個數的和與一個數相乘，可以用這兩個數分別同這個數相乘，再把兩個積相加，結果不變，這叫做乘法分配律，用字母表示就是：（a＋b）×c=a×c＋b×c。能不能擴大乘法分配律的使用范圍呢？例如，兩個數的差與一個數相乘，用這兩個數分別與這個數相乘，再把兩個積相減，結果會不會改變呢？也就是能不能用字母表示為“（a－b）×c=a×c－b×c”呢？

為了回答這個問題，你不妨先計算，再比較下面兩組算式：

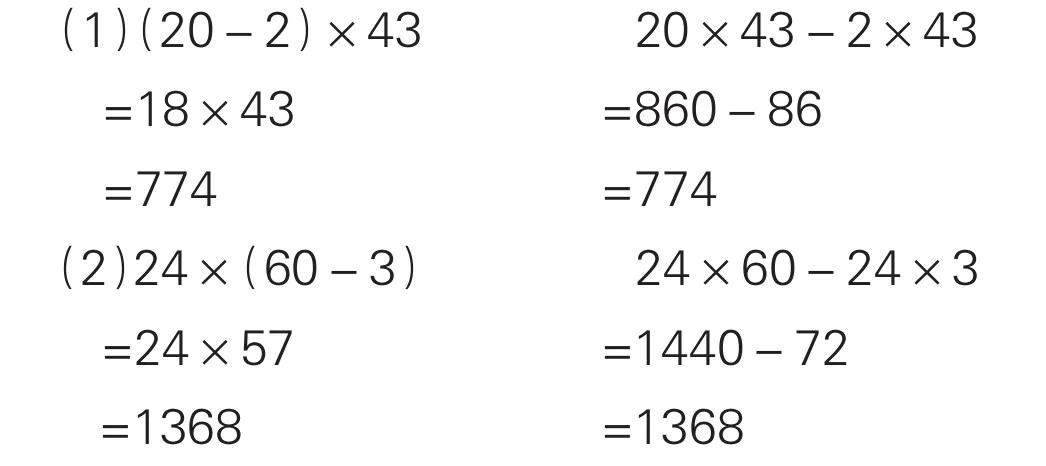
由此可見，（20－2）×43=20×43－2×43，24×（60－3）= 24×60－24×3。兩個例子還不能說明問題，你不妨再多舉幾個類似的例子算一算，比一比。

通過計算比較，我們會發現，由乘法分配律推廣出來的“（ab）×c=a×c－b×c”是正確的。利用這一結論，我們可以將一些計

算變得簡便起來。

例如：36×18=36×（20－2）=36×20－36×2=720－72= 648。

再如：

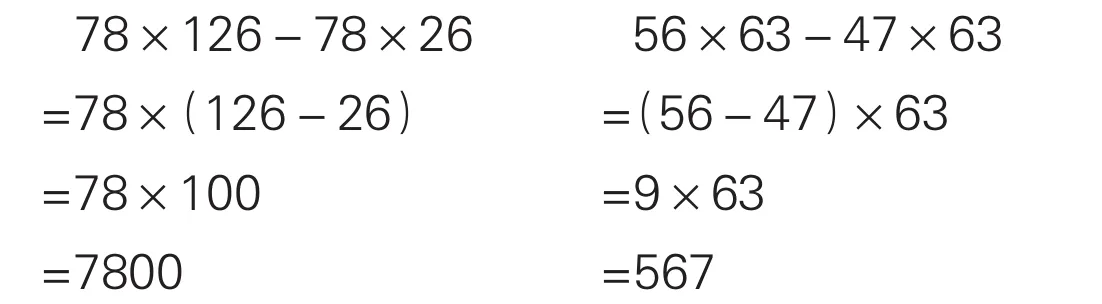
小朋友，要是兩個數的和除以一個不為0的數，是不是可以用這兩個數分別除以這個數，再把兩個商相加呢？即用字母表示為“（a＋b）÷c=a÷c+b÷c（c≠0）”。兩個數的差除以一個不為0的數呢？你還能想出哪些類似的問題？趕快開動腦筋探索一下吧！

（作者單位：江蘇省興化市沈倫中心小學）