封閉圖形“內部”與“外部”的辨別探究

洪偉++郜舒竹

【摘 要】判斷某點是處于一個閉合圖形的內部還是外部，看起來是一個很簡單的問題，但在一定條件下也會變得非常復雜。“內部還是外部”的學習活動即是讓學生通過實踐操作探索如何用數學方法解決該問題，發現規律，總結方法。學生將在知識技能、情感體驗、數學思維、個性品質與社會性等多方面得到提升。

【關鍵詞】封閉圖形 內部 外部 規律

“內部還是外部”這個學習活動即是將一段細線打結形成閉合線圈，通過改變線圈的形狀形成幾個不同的閉合曲線圖形，探索如何更便捷、準確地判斷一枚一角硬幣處于這幾個曲線圖形的內部還是外部的方法。

通過該學習活動學生會發現，原本一些感覺上非常簡單、司空見慣或者顯而易見的概念在一定條件下也會變得模糊不清、難以界定，也需要認真研究和探索。對于一些基本圖形來說內部和外部可以一眼看出，很好判斷，如長方形、三角形、梯形等，因此人們往往忽略對這種看似平常概念的深入探究和思考。活動提供一次范例引起學生對這些平常概念的關注和思考，適合小學五年級教學。

在該學習活動中學生將完整經歷發現問題、探索問題、提出假設、驗證假設、解決問題的全過程，并經歷從簡單到復雜再回到簡單后又復雜化的情感體驗。學生將體會到數學問題的模型化可以將具體的實際問題抽象成數學問題并使其得以簡單清晰地解決，體會到數學的實用性和數學證明的嚴謹性。活動中展現出來的簡單與復雜之間的反差及相互轉化對學生思維具有很好的啟迪作用。

活動中學生需要小組分工合作，組員分別輪流承擔出題人、解題人和協助者的角色，并協作完成活動任務。學生的表達能力、溝通能力、分工協作能力和實踐操作能力都將得到鍛煉。

一、問題與動機

探討一個點處于一個幾何圖形的內部還是外部看起來是一個非常簡單的問題，但如果這個幾何圖形是一個閉合的曲線圖形，問題還是不是那么簡單呢？如果這個曲線圖形非常復雜，如何更有效、更快捷地判斷出哪是內部哪是外部呢？

提出問題、引發思考這一環節需要教師把握課堂節奏、營造適宜氣氛，生動地展現問題的簡單與復雜之間的反差，引發學生的興趣和探索欲。教師分三步展示圖1、圖2、圖3，每次詢問學生圖中的一角硬幣處于圖形的內部還是外部。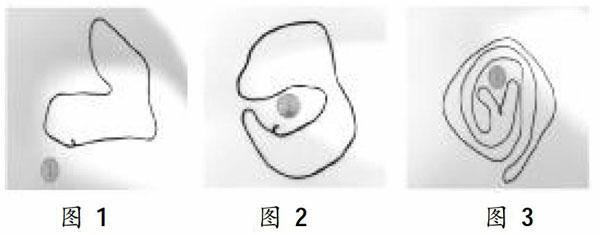

展示圖1和圖2時學生一般會認為問題實在是太簡單了，然后教師給出圖3，展示反差，并詢問如果圖形再復雜一些，用觀察法判斷不出來，怎么辦。拋出疑問，引發接下來的探索活動。

活動的主要內容是引導學生通過對幾個不同閉合曲線圖形內部外部的判斷，探索總結規律，建立簡單數學模型。需要準備的學習用具包括：一段1米長的細繩、一枚一角硬幣、一枚五角硬幣、一把30厘米長的直尺。

二、過程與設計

感知到從簡單到復雜的反差后，教師可以給學生一小段自由討論和思考的時間。學生可以先進行天馬行空的想象，因為與書本上學過的知識看起來關系不大，學生受到的束縛和思維定勢的影響較小，利于發散性思維的培養。通常情況下經過討論后學生會給出一些直觀的辦法，例如直接觀察，把曲線圖形看成迷宮、硬幣看成小蟲子嘗試能不能找到出路，把曲線圖形進行適當的變形處理再觀察判斷，等等。將該問題與數學知識關聯起來總結歸納出一般化解決方法的概率較小。學生自己有了一定的思考后，教師再介紹本活動的探索步驟，更有利于其體會數學在解決實際問題中的作用。

教師將學習用具分發給學生，并介紹活動步驟如下：

1.所有學生分成3～4人的小組，組員之間自行商量分工事宜，選出組長、發言人、記錄員等角色。

2.取出細繩，并將兩端系成一個結，形成一個閉合線圈。

3.將閉合線圈平放在桌面上，并將兩枚硬幣放在線圈的外部，注意使兩枚硬幣間的距離不超過30厘米（即直尺的長度）。

4.一名同學操作線圈，改變它的形狀，使其圍繞一角硬幣形成一個較為復雜的閉合圖形。注意線圈不能離開桌面，以保證兩枚硬幣始終處于線圈的外部。然后用直尺將兩枚硬幣連接起來，觀察直尺所在的連接線段穿過線圈有幾個交點，將結果記錄在如下表 1所示的活動記錄單中。每位同學輪流操作一次，注意使每次的線圈形狀盡可能不同。教師可以先示范操作一次，學生有問題先提出解決，再小組展開活動。

5.活動結束后，小組內先討論記錄下的交點個數有什么規律，試著總結規律，提出判斷硬幣處于曲線圖形內部還是外部的方法。

三、規律與建模

小組活動結束后，每組的發言人上臺講解自己小組的發現與結論，教師組織全班展開討論，使結論盡可能完善并引導學生用數學語言表達結論使之模型化。例如，用模型化的語言可以概括成：“要判斷曲線圖形上一點A處于圖形的內部還是外部，可以在圖形外建立另一點B，連接A和B形成線段AB，線段AB穿過曲線圖形的交點個數記為n。當n為偶數時，點A處于曲線圖形的外部。”模型的建立使具體的實際問題變成抽象的數學問題，復雜的問題又回歸簡單。

四、總結與反思

活動中學生經歷的思維過程包括：實踐操作、發現規律、歸納推理、模型化表達。規律指的是運動或變化過程中的不變因素。[1]活動中曲線圖形和交點個數都是變化的，交點個數的奇偶性與內外部之間的對應關系是其中的不變因素。

從發現規律到提出結論運用的數學思維是歸納推理。從邏輯的角度說，歸納（induction）推理指的是人依據自身的意愿、經驗和當前感知，從事實（fact）到推論（inference）的思維方式。[2]從有限個曲線圖形中總結出的規律是經驗和當前感知，用于判斷內部還是外部的一般化方法是推論。由于曲線圖形的種類和個數都是無窮多個，這里用的是不完全歸納，因此結論是否正確存在著不確定性。教師可以根據課堂情況引導學生質疑結論，引發其課后進行進一步的探索和思考。于是簡單的結論如果想要嚴密的證明又似乎變得復雜了。整個探索過程學生體驗到數學問題在簡單和復雜間不斷地奇妙變化，收獲豐富的情感體驗。

最后全班討論環節使得結論得以模型化表達，學生可以體會到數學符號的簡潔高效和數學語言的嚴謹性。

五、關聯與拓展

開展該學習活動所需的用具很簡單，學生課后可以自己準備用具繼續探索兩個問題：第一，當n為奇數時，點A是否處于曲線圖形內部，改變曲線圖形的形狀多次驗證并填寫活動記錄單；第二，嘗試尋找反例。

教師可以引入數學史上類似運用不完全歸納法提出的著名數學問題，如哥德巴赫猜想等，引導有興趣的同學進一步查閱相關資料拓展研究，思考有什么方法可以嚴密地證明課上提出的數學模型正確與否。

參考文獻：

[1]郜舒竹.“探索規律”釋義[J].課程·教材·教法，2015（1）.

[2]郜舒竹.小學數學這樣教[M].上海：華東師范大學出版社，2015：137.

（首都師范大學初等教育學院 100048）