基于貝葉斯理論的測量誤差預(yù)報與修正方法
馮 云,朱亦丹,李 將
(中船重工海博威(江蘇)科技發(fā)展有限公司,揚州 225000)
?
基于貝葉斯理論的測量誤差預(yù)報與修正方法
馮 云,朱亦丹,李 將
(中船重工海博威(江蘇)科技發(fā)展有限公司,揚州 225000)
針對動態(tài)測量過程的復(fù)雜性以及隨機性,提出了基于貝葉斯理論的動態(tài)測量誤差的建模、預(yù)報方法。該方法要求的數(shù)據(jù)量少,對動態(tài)測量誤差序列的平穩(wěn)性沒有要求,并且能夠充分利用預(yù)報過程中的主、客觀信息來實時修正模型,提高預(yù)報精度。最后,通過Labview仿真驗證了基于貝葉斯理論的動態(tài)測量誤差預(yù)報方法具有較高的預(yù)報精度。
貝葉斯動態(tài)模型;誤差預(yù)報;動態(tài)誤差;實時修正
0 引 言
動態(tài)測量日益普及,對動態(tài)測量精度的要求也越來越高,誤差修正是提高動態(tài)測量精度的一種有效方法,因此受到普遍關(guān)注和高度重視。根據(jù)已知的測量誤差序列建立動態(tài)測量誤差模型,并對將來時刻的測量誤差進行預(yù)報,是實現(xiàn)動態(tài)測量誤差實時修正的基本方法。國內(nèi)外專家、學(xué)者對動態(tài)測量誤差的建模預(yù)報方法進行了大量研究,并提出了很多有效方法,比如時序分析法[1]、諧波分析法、灰色理論法[2]、神經(jīng)網(wǎng)絡(luò)法[3]等現(xiàn)代數(shù)學(xué)方法。這些方法分別針對特定特征的誤差序列提出,具有一定的實用性;但是也存在一些不足,比如需要較多的測量數(shù)據(jù),對測量誤差序列的平穩(wěn)性也有要求,模型比較簡單,對異常情況的響應(yīng)差等。另外,由于動態(tài)測量誤差的隨機性和時變性[4],導(dǎo)致模型的誤差預(yù)報精度會隨著預(yù)報步數(shù)的增加而快速降低,嚴重影響了動態(tài)測量誤差的實時修正效果,成為阻礙進一步提高動態(tài)測量誤差修正精度的關(guān)鍵所在。對此,本文提出了動態(tài)測量誤差的貝葉斯建模預(yù)報方法。該方法要求的數(shù)據(jù)量較少,且對誤差序列沒有平穩(wěn)性要求,能夠充分利用預(yù)報過程中的主客觀信息來實時修正模型,提高測量誤差的預(yù)報精度。
1 動態(tài)測量誤差的貝葉斯建模、預(yù)報理論
基于貝葉斯預(yù)報理論的動態(tài)測量誤差預(yù)報方法[5],第1步是根據(jù)已獲取的測量誤差序列建立動態(tài)測量誤差模型。測量誤差序列可以通過觀測方程和狀態(tài)方程來描述:

(1)
狀態(tài)方程:θt=Gtθt-1+ωt
(2)
式中:yt為t時刻動態(tài)測量的誤差值;本文主要針對單次測量誤差序列進行研究,因此,yt和υt是一維變量;θt、ωt的維數(shù)以及Ft、Gt根據(jù)動態(tài)誤差序列的特征來決定;υt、ωt分別為觀測誤差矩陣、狀態(tài)誤差矩陣,它們互相獨立。
對于一般的動態(tài)測量誤差預(yù)報方法,要獲得θt的初始信息和υt、ωt的先驗分布很難,因此本文采用無信息先驗分布法進行測量誤差的預(yù)報。假設(shè)誤差模型中一共有n個變量,則可以根據(jù)n個已知的測量誤差值來確定θt、υt以及ωt的初始信息。根據(jù)測量誤差的特點以及簡化推導(dǎo),假設(shè)υt為正態(tài)分布N[0,V](V為未知變量),ωt為均值等于0、方差等于Wt的T分布。由于使用了較少的測量誤差數(shù)據(jù)確定初始信息,并且不可能根據(jù)這些數(shù)據(jù)估計出參數(shù)的變化趨勢,因此,可以設(shè):Wt=0(t=1,2,…,n)。
設(shè)t時刻及之前所有時刻的有效信息集合為Dt,t=0時的初始有效信息集合為D0。根據(jù)無信息先驗分布法可得:
p(θ1,V|D0)∝V-1(V>0)
(3)
根據(jù)貝葉斯理論及測量誤差點{y1,y2,…,yn},可得到p(θn,V|Dn),進而獲得(θn|Dn)和(V-1|Dn)的邊緣分布;然后將上述邊緣分布作為初始信息,對動態(tài)測量誤差進行遞推預(yù)報(t>n)。
設(shè)誤差數(shù)據(jù)的初始信息為:
ωt~Tnt-1[0,Wt]
(4)
(θt-1|Dt-1)~Tnt-1[Mt-1,Ct-1]
(5)
(θt|Dt-1)~Tnt-1[At,Rt]
(6)
(V-1|Dt-1)~Γ(nt-1/2,dt-1/2)
(7)

一步向前預(yù)報為:
(yt|Dt-1)~Tnt-1[ft,Qt]
(8)

遞推修正關(guān)系為:
(θt|Dt)~Tnt[Mt,Ct]
(9)
(V-1|Dt)~Γ[nt/2,dt/2]
(10)
Mt=At+Btet
(11)
Ct=(St/St-1)[Rt-BtBtTQt]
(12)
St=dt/nt
(13)
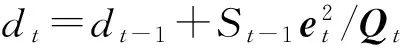
根據(jù)公式(9)~(13)可知,遞推算法中需要知道Wt(t>n)的值,采用比例因子法,可得:
(14)
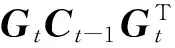
(15)
則:
Wt=GtCt-1GtT(ρ-1-1)
(16)
對于第k(k>0)步向前預(yù)報分布:
(θt+k|Dt)~Tnt[At(k),Rt(k)]
(17)
(yt+k|Dt)~Tnt[ft(k),Qt(k)]
(18)

2 軟件仿真與分析
2.1 程序設(shè)計
本次設(shè)計是基于貝葉斯動態(tài)誤差理論,采用無信息先驗分布法,以Labview軟件為平臺,進行動態(tài)測量誤差的實時預(yù)報與修正。圖1所示為動態(tài)測量誤差貝葉斯預(yù)報程序設(shè)計流程圖。
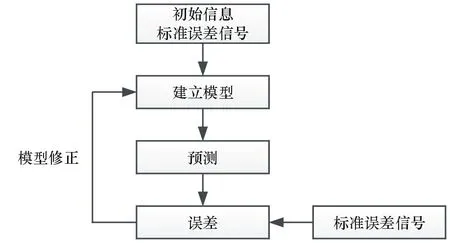
圖1 動態(tài)測量誤差貝葉斯預(yù)報程序流程圖
2.2 仿真與分析
為了驗證動態(tài)測量誤差建模及預(yù)報修正的效果,本文采用周期信號和線性信號的疊加信號對實際效果進行驗證。采用的信號為:
y=5sin(20πx)+5sin(40πx)+5sin(80πx)+1·400x
其波形如圖2所示。
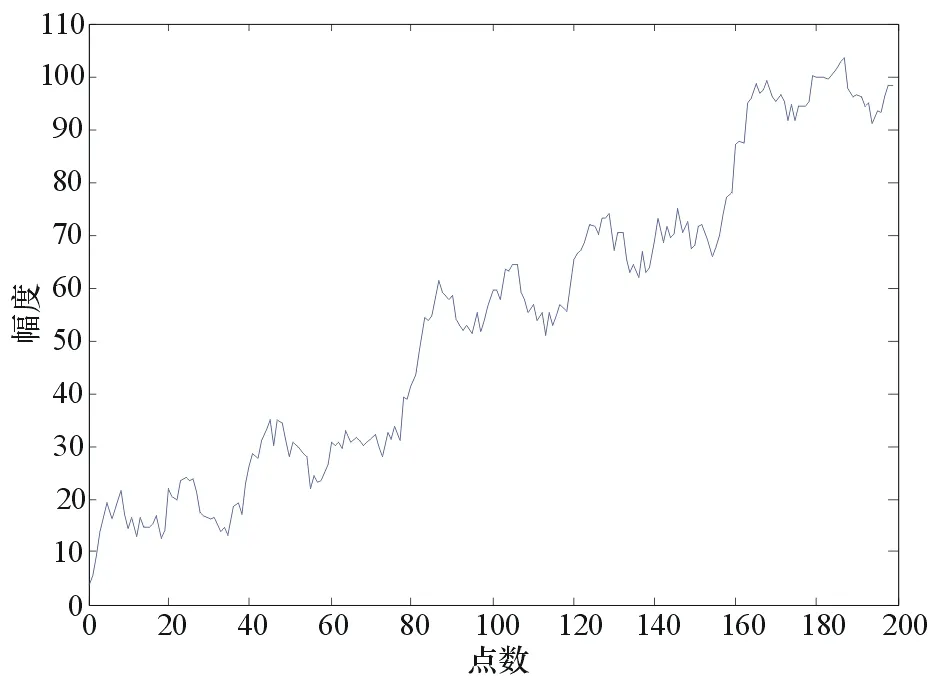
圖2 輸入信號波形
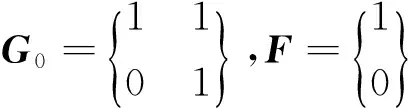
對于周期性模型,周期p=40。根據(jù)貝葉斯理論,可求得它有q=p/2=20個調(diào)和分量與水平分量。但其主要的調(diào)和分量有3個,r=1[y=sin(20πx)],r=2[y=sin(40πx)],r=4[ysin(80πx)],則:
(19)
由模型疊加原理可知:G=diag(G1,G2,G3),F(xiàn)=(1,0,1,0,1,0)T。
對于p=40,其未知參量數(shù)目N=2(q-1)+1=39。
對于線性信號和周期信號的疊加信號,根據(jù)疊加原理,可以得到:N=3+39-1=41;F=(1,0,1,0,1,0,1,0)T;G=diag(G0,G1,G2,G3)。
運行程序后可得到波形如圖3所示。
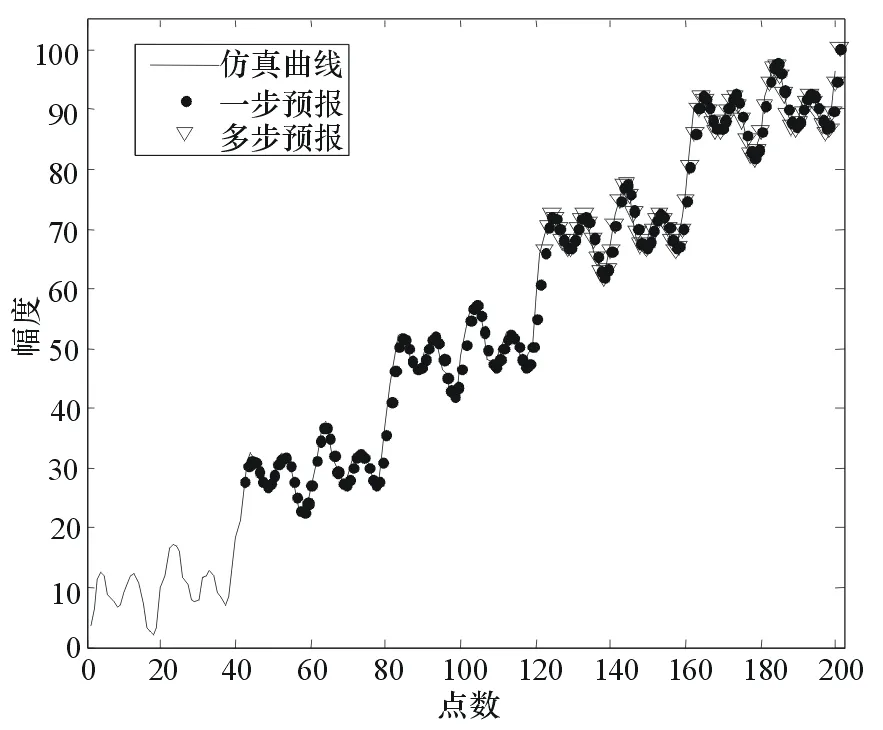
圖3 多步預(yù)報波形圖
從圖3可以看出:從40到80的一步預(yù)報效果非常好,和原曲線基本重合,對動態(tài)誤差序列的模型
建立比較好;從120到200的多步預(yù)報中能夠反映出原曲線的趨勢,預(yù)報誤差比較小。
3 結(jié)束語
本文采用的貝葉斯預(yù)報建模方法,對動態(tài)測量誤差序列沒有平穩(wěn)性要求,使用數(shù)據(jù)較少,能夠快速有效地實時修正誤差模型,因此模型的適應(yīng)性好,能處理異常情況的發(fā)生,提高了動態(tài)誤差實時修正的精度。最后,通過線性信號和周期信號的疊加信號進行了仿真驗證,實驗結(jié)果表明,一步預(yù)報和多步預(yù)報的結(jié)果與實際數(shù)據(jù)誤差不大,預(yù)報精度高。由此可知,基于貝葉斯理論的動態(tài)測量誤差建模預(yù)報方法能夠非常好地預(yù)報動態(tài)測量誤差。
[1] 盧榮勝.動態(tài)測量實時誤差修正技術(shù)研究[D].合肥:合肥工業(yè)大學(xué),1998.
[2] 龔蓬.動態(tài)測量誤差修正灰色建模理論與應(yīng)用技術(shù)研究[D].合肥:合肥工業(yè)大學(xué),1999.
[3] 葉兵.基于遺傳神經(jīng)網(wǎng)絡(luò)模型實時誤差修正任意角測量系統(tǒng)[D].合肥:合肥工業(yè)大學(xué),2004.
[4] 費業(yè)泰,盧榮勝.動態(tài)測量誤差修正原理與技術(shù)[M].北京:中國計量出版社,2001.
[5] 程真英.動態(tài)測量誤差修正灰色建模理論與應(yīng)用技術(shù)研究[D].合肥:合肥工業(yè)大學(xué),2004.
PredictionandCorrectionMethodofMeasurementErrorsBasedonBayesTheory
FENGYun,ZHUYi-dan,LIJiang
(CSICHebowi(Jiangsu)TechnologyDevelopmentCo.,Ltd,Yangzhou225000,China)
Inviewofthecomplexityandrandomnessofdynamicmeasurementcourse,modelingandpredictionmethodfordynamicmeasurementerrorsbasedonBayestheoryispresented.Themethodrequireslessdata,andthestabilityofdynamicmeasurementerrorssequenceisnotrequired.Themethodcanmakefulluseofthesubjectiveandobjectiveinformationtocorrectthemodelinrealtime,improvesthepredictionaccuracy.Finally,LabviewsimulationresultprovesthatthepredictionmethodofdynamicmeasurementerrorsbasedonBayestheoryhasbetterpredictionaccuracy.
Bayesdynamicmodel;errorprediction;dynamicerror;realtimecorrection
2016-05-27
TP
A
CN32-1413(2016)05-0064-03
10.16426/j.cnki.jcdzdk.2016.05.016

