基于群組層次分析法與云模型的情報保障效能評估*

黃俊華 楊 桄 張筱晗 楊永波

(空軍航空大學 長春 130022)

?

基于群組層次分析法與云模型的情報保障效能評估*

黃俊華 楊 桄 張筱晗 楊永波

(空軍航空大學 長春 130022)

情報保障效能評估是情報保障中一項重要的內容，根據情報保障的要素與指標建立原則，論文構建了一個情報保障效能評估指標體系。為了降低情報保障效能評估的主觀性與不確定性，論文提出了一種結合群組層次分析法與云模型評估的效能評估方法。最后，通過實例仿真驗證了方法的有效性與實用性。

情報保障; 效能評估; 群組層次分析法; 云模型

Class Number E92;TJ012.4

1 引言

一體化聯合作戰將是未來戰爭的必然趨勢，美軍十分注重情報保障在一體化聯合作戰中的運用，將情報保障視為戰爭的“力量倍增器”[1]。在情報保障工作中，美軍對于情報保障的效能評估也相當的重視，將情報保障效能評估貫穿至整個美軍情報周期中[2]，對情報保障工作及時做出評估和反饋，提高情報保障作業的效率。故對情報保障效能評估的研究具有重要的意義，通過效能評估，能夠準確地了解情報保障工作的運行情況以及對作戰的情報支援程度。本文從情報保障效能評估體系的建立與情報保障效能評估方法的選擇兩方面進行研究。

2 指標體系的建立

指標體系的建立是效能評估工作的核心，科學合理的指標體系是準確評估的關鍵。建立情報保障指標體系首先要滿足指標選取的基本原則，即：完備性，科學性，可測、可控性。

在繼承效能評估指標體系建立基本原則的基礎上，情報保障效能評估的選取要滿足情報保障的要素與要求。美軍對于聯合作戰情報保障工作以及情報產品提出了以下幾個標準[1]：及時性、客觀性、可用性、可供性、完整性、準確性、相關性。根據這一標準本文建立情報保障效能評估指標體系，如圖1所示。

圖1 情報保障效能評估指標體系圖

3 情報保障效能評估方法

3.1 評估方法的選擇

情報保障效能評估的部分指標很難用具體的數值來表示，只能用語言來描述。云模型評估法能夠同時有效而簡便地實現定性與定量相互轉換，可將模糊性和隨機性結合在一起，充分實現精確數值與定性語言之間的轉換。

情報保障效能評估工作不是一人完成，每個決策者的知識水平以及個人喜好的差異都會對同一個問題產生不同的觀點。群組層次分析法是在層次分析法的基礎上改進的，能夠將個人判斷綜合成較為合理的結果[3]。

本文根據上述特性，采用群組層次分析法與云模型評估法相結合的情報保障效能評估方法，其步驟為

1) 根據群組層析分析法確定指標體系的指標權重。

2) 求各指標的云模型表示。

3) 用一個綜合云表示系統狀態。

4) 用加權偏離度來衡量綜合云重心的改變。

5) 用云模型的評語集實現效能評估。

3.2 基于群組層次分析法的指標權重確定

3.2.1 建立判斷矩陣

確定情報保障指標體系的權重的關鍵一步是確定同級指標的相對重要性，不同的側重點會對情報保障的評估帶來不同的結果。本文采取專家法來確定各指標的相對重要性，評估專家要以特定任務為背景，根據情報保障的要求來確定各性能指標的重要性。

在某一指標下，對于n個元素中的任意兩個元素a和b，通過經驗對比獲得a和b兩個元素的相對重要性。目前多使用9/9～9/1標度法來為元素的重要性賦值[4]，比例標度如表1所示。

表1 9/9～9/1標度法

通過9/9～9/1標度法可以分別構建一級指標的判斷矩陣E-B和二級指標的判斷矩陣B1-C，B2-C和B3-C，在此以E-B為例。

判斷矩陣E-B所表示的是情報保障效能指標、情報質量效能指標和戰場態勢感知效能指標的相對重要性，表示為：

(1)

式中aij表示Bi相對Bj的相對重要性。

可同理根據式(1)構造二級指標的判斷矩陣B1-C，B2-C和B3-C。

判斷矩陣是一種正互反矩陣，矩陣中的各元素滿足：

(2)

當判斷矩陣中的元素滿足傳遞性時，即：

aij·ajk=aik

(3)

可稱該矩陣為一致性矩陣[5]在根據判斷矩陣導出各指標的排序權重時，一致性矩陣有重要的意義。

3.2.2 計算指標權重

計算各級指標的權重就是對各級指標的判讀矩陣A進行最大特征根λmax對應向量W的求解[6]，表達式為

A·W=λmax·W

(4)

對W進行歸一化處理后得到指標Bk下各指標元素的排序權重。

對λmax和W進行一致性檢驗[7]：

1) 計算一致性指標C.I.

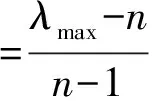
(5)

2) 查找相應的平均隨機一致性指標R.I.，如表2所示。

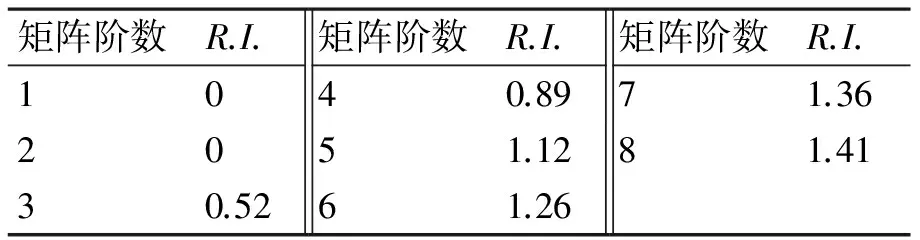
表2 平均隨機一致性指標R.I.

3) 計算隨機一致性比例C.R.

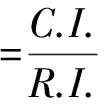
(6)

當C.R.≤0.1時，判斷矩陣的一致性是可以接受的。

3.2.3 生成群組權重向量

計算出各專家給出的判斷矩陣的權重排序向量后，為進一步消除主觀因素，提高權重排序向量的可信性與準確性，要綜合各專家指標排序向量計算群組權重排序向量。計算群組權重排序向量的方法有加權算術平均法和加權幾何平均法兩種[8]，本文采用加權算術平均法。

各專家的排序向量的加權算術平均記為W=(w1,w2,…,wn)T，即：

wj=λ1wj1+λ2wj2+…+λswjs

(7)

(8)

式中，λk表示為第k個專家的權重，本文將專家的權重視為同等重要，即:λ1=λ2=…=λs。

3.3 基于云模型的效能評估[9]

3.3.1 指標的云模型表示

云[10]是用語言值表示的某個定性概念與定量表示之間的不確定性轉換模型，它主要反映概念上的不確定性，即模糊性和隨機性。云的數字特征用3個參數來描述，即：期望值Ex，能代表定性概念的數值；熵En，為概念不確定程度的度量，熵越大，概念相對越模糊；超熵He，為熵的不確定程度的度量，即熵的熵，反映了云的離散程度。3個數字特征整體表征一個概念，記做CG(Ex,En,He)。

指標體系中的指標表示形式既有數值型的，也有用語言表述的。根據云理論，提取指標體系中的n組樣本組成決策矩陣，對于數值型表示的指標與語言表述型的指標可以用兩個云模型進行表示：

1) 數值型指標

Ex=(Ex1+Ex2+…+Exn)/n

(9)

(10)

式中：Ex1,Ex2,…,Exn為指標量的值。

2) 語言表述型指標

(11)

En=En1+En2+…+Enn

(12)

式中Ex1,Ex2,…,Exn為指標云模型的期望值，En1,En2,…,Enn為指標云模型的熵。

3.3.2 生成指標綜合云

p個指標可以用p個云模型表示，p個云模型反映的指標體系的狀態可以用一個p維綜合云模型表示。當指標體系的狀態改變時，綜合云的狀態也會隨之改變，相應的云重心也會發生變化。綜合云的云重心T用p維向量表示，即：

T=(T1,T2,…,Tp)

(13)

Ti=ai×bi(i=1,2,…,p)

(14)

3.3.3 衡量云重心的改變

假設理想狀態下p維綜合云的重心位置向量為

(15)

云重心高度向量為

(16)

則理想狀態下的云重心向量為

(17)

某一狀態下的指標體系的云重心為T=(T1,T2,…,Tp)。

用加權偏離度θ來衡量這兩種狀態下綜合云的重心的差異，θ值越小表示差異越不明顯，θ值越大表示差異越顯著。將綜合云的云重心向量歸一化，得到向量TG，歸一化公式如式(18)、式(19)所示：

(18)

(19)

經歸一化后的指標體系狀態的綜合云的重心向量均為有大小有方向的值，經歸一化后理想狀態下的云重心量為(0,0,0,0)。

把各指標歸一化之后的向量值乘以其權重值然后再相加即得到加權偏離度θ：

(20)

3.3.4 用云模型實現評測的評語集

根據云模型理論，本文建立由11個評語所組成的評語集V=(v1,v2,…,v11)，v1～v11分別表示極差、非常差、很差、較差、差、一般、好、較好、很好、非常好、極好等11個評語，將11個評語置于連續的語言值標尺上，并且用云模型來表示每個評語值，建立一個定性評測的云模型評測器如圖2所示。

圖2 云模型評測器

指標體系理想狀態視為極好，其θ=0；系統的θ值越小則表示系統在某一狀態下與理想狀態越接近，性能越好，反之亦然。

對于一個具體方案，將求得的θ值輸入評測云發生器中，可能會激活兩種情況：一是激活某個評語值云對象的程度要遠大于其他評語值云對象，此時視該評語值為該方案的評價結果；二是激活了兩個評語值云對象，且激活程度相差不大，這時可以運用綜合云生成一個新的云對象，將其期望值作為評測結果(定量結果)輸出，而此期望值對應的定性表述可由專家或系統用戶另外給出[11]。

4 實例仿真

本文以模擬實例進行仿真，選取五名專家對某次情報保障行動進行評估。限于篇幅，本文將對指標B2進行效能評估。

1) 根據群組層次分析法確定指標B2下各指標元素的權重值。

構建某名專家對指標B2下各指標元素的判斷矩陣B2～C：

可得某專家的指標B2下各指標元素的權重分別是0.1044，0.1148，0.2341，0.3176，0.2292。同理可對其他四名專家的指標B2下各指標元素的權重進行計算；然后進行一致性檢驗，不滿足的專家要進行反饋調整，直到符合一致性檢驗；最后利用加權平均的方法進行群組決策計算。限于篇幅，省略詳細步驟，只給出指標B2的群組權重排序向量，如下所示：

Wk=(0.1065,0.1179,0.2355,0.3123,0.2246)

2) 五名專家根據語言標尺對某次情報保障行動進行評估，如表3所示。

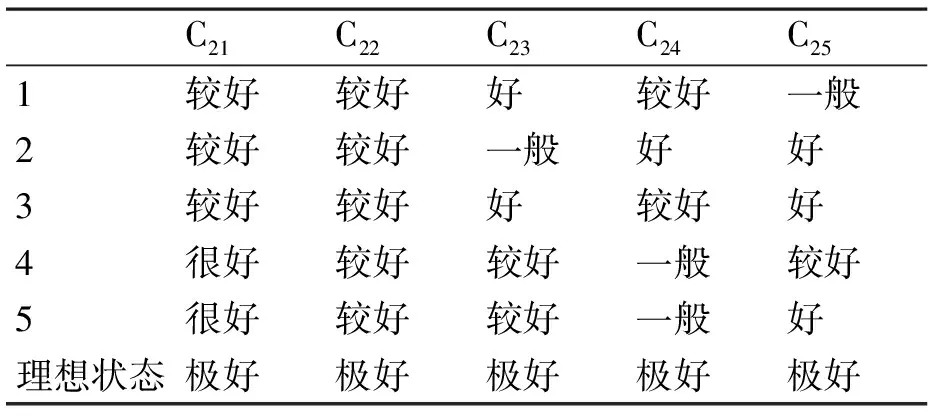
表3 五名專家的評價值

3) 根據云理論，將5名專家的語言評價值用(Ex,En,He)3個數字特征進行表述。由表3與語言標尺可得決策矩陣G：

4) 根據決策矩陣G可得各指標云模型的期望與熵，如表4所示。

表4 各指標的期望值與熵

5) 根據云理論，計算加權偏離度。

由式(14)，可得5維加權綜合云的重心向量為(0.0788,0.0849,0.1460,0.1874,0.1348)，理想狀態的5維加權綜合云的重心向量為(0.1065,0.1179,0.2355,0.3123,0.2246)。

由式(19)歸一化分別得：(-0.2600,-0.2800,-0.3800,-0.4000,-0.4000)和(0,0,0,0,0)。

由式(20)計算得θ=-0.2751。即評估結果的偏離度距離理想狀態為-0.2751，其評估記過為0.7249，將其輸入云發生器中可激活“較好”與“很好”兩個對象，且激活程度更偏向于較好，故指標B2的評估結果為介于“較好”與“很好”之間，且偏向于較好，最終評估值為0.7249。

5 結語

情報保障效能評估是個主客觀信息相結合的多元集成的復雜過程。本文在情報保障理論的基礎上建立了情報保障效能評估指標體系，根據情報保障的要素與特點，結合群組層次分析法與云模型評估相結合的方法，將主觀影響因素綜合集成，降低評價的主觀性，將模糊性和隨機性進行了較好的轉換，有效地解決了情報保障效能評估中的不確定性與主觀性，為情報保障效能評估的研究提供了依據。

[1] 張曉軍.美國軍事情報理論研究[M].北京:軍事科學院出版社,2007:235-236.

[2] 孫建明.戰后情報偵察技術發展史研究[M].北京:軍事科學院出版社,2008:290-292.

[3] 林岳崢,祝利,程曉雷.基于群組層次分析法的情報保障系統效能評估[J].兵工自動化,2012,31(8):57-61.

[4] 趙全仁,邱志明,竇守健.等武器裝備論證導論[M].北京：兵器工業出版社,1998:96-112.

[5] 劉強.國防系統分析方法:下冊[M].北京：國防工業出版社,2003:531-537.

[6] 王威,崔明明.復雜系統評估的綜合層次分析法[J].海軍工程大學學報,2006(2):42-46.

[7] 楊智,董長清.改進層次分析法在雷達網探測效能評估的應用[J].空軍雷達學院學報,2007(3):14-17.

[8] 郭齊勝,揚秀月,王杏林,等.系統建模[M].北京：國防工業出版社,2006:298-299.

[9] 焦利明,于偉,羅均平,等.基于云重心評判法的指揮自動化系統效能評估[J].情報指揮控制系統與仿真技術,2005,27(5):71-74.

[10] 李德毅,劉常昱,杜鶿,等.不確定性人工智能[J].軟件學報,2004,15(9):1583-1594.

[11] 湯君,趙文杰,李德軍.基于云模型的戰場情報綜合效能評估[J].艦船電子工程,2012,32(6):37-40.

Information Security Effectiveness Evaluation Based on GAHP and Cloud Model

HUANG Junhua YANG Guang ZHANG Xiaohan YANG Yongbo

(Aviation University of Air Force, Changchun 130022)

Intelligence security effectiveness evaluation is an important content of information security. According to the elements of information security and the principle of index establishment, the paper constructs an index system of intelligence security effectiveness evaluation. In order to reduce the subjectivity and uncertainty of information security effectiveness evaluation, the paper proposes a method of information security effectiveness evaluation based on GAHP and cloud model. Finally, the validity and practicability of the method are verified by an example simulation.

information security, effectiveness evaluation, GAHP, cloud model

2016年5月10日,

2016年6月26日

吉林省科技發展計劃資助項目(編號：20140101213JC)；吉林省教育廳“十二五”科研項目(編號：2015448)資助。

黃俊華,男，碩士研究生，研究方向：遙感圖像解譯。楊桄,男，博士，副教授，研究方向：遙感圖像解譯與地理信息系統。

E92;TJ012.4

10.3969/j.issn.1672-9730.2016.11.025