隔離小生境粒子群算法在地鐵列車運行曲線優(yōu)化中的應用

田志鵬 米根鎖 王寶寶

(1.蘭州交通大學自動化與電氣工程學院,730070,蘭州;2.上海卡斯柯信號有限公司,200070,上海∥第一作者，碩士研究生)

?

隔離小生境粒子群算法在地鐵列車運行曲線優(yōu)化中的應用

田志鵬1米根鎖1王寶寶2

(1.蘭州交通大學自動化與電氣工程學院,730070,蘭州;2.上海卡斯柯信號有限公司,200070,上海∥第一作者，碩士研究生)

針對地鐵列車運行優(yōu)化指標過于單一的問題,提出了牽引-巡航-惰行-制動模式運行曲線的計算流程,綜合考慮能耗、乘客舒適度、運行時間、停車精度等指標,用Fi(綜合優(yōu)化目標函數(shù))值度量綜合運行質量(其值越小表示越接近理想狀態(tài)),并建立列車運行曲線的優(yōu)化模型。結合粒子群算法和小生境技術,設計了應用于列車運行曲線優(yōu)化的隔離小生境粒子群算法(INPSO)。結合實例仿真,利用INPSO優(yōu)化模型,確定最優(yōu)惰行末端速度,實現(xiàn)了高質量列車運行曲線的計算。其中INPSO優(yōu)化后的Fi值實際只是基本粒子群算法優(yōu)化結果的58.96%,效果顯著,證明了INPSO尋優(yōu)的有效性以及可靠性。

地鐵； 列車運行曲線優(yōu)化; 綜合運行質量; 隔離小生境粒子群算法

First-author′s address School of Automation and Electrical Engineering,Lanzhou Jiaotong University,730070,Lanzhou，China

地鐵列車運行曲線的計算是實現(xiàn)綜合優(yōu)化運行的基礎,也為列車運行實時控制的改進提供一種思路。文獻[1]利用遺傳算法對惰行控制進行優(yōu)化，從而實現(xiàn)了地鐵列車的多目標運行,但沒有考慮舒適度指標。文獻[2]分析了地鐵運行的原理,利用遺傳算法綜合優(yōu)化多區(qū)間的運行曲線和停站時間,但沒有綜合考慮各運行指標。文獻[3]對列車運行曲線進行了優(yōu)化,但只考慮了時間和能耗指標。文獻[4]利用粒子群算法優(yōu)化了高鐵列車的運行策略,得到了綜合考慮多個指標的控制策略,但其沒有考慮舒適度指標，且高鐵的情況并不完全適用于地鐵。

本文設計了通過惰行末端速度確定列車運行曲線的計算流程,建立了綜合考慮各運行指標的優(yōu)化模型，通過隔離小生境粒子群算法的優(yōu)化,得到了最優(yōu)的惰行末端速度,實現(xiàn)了高質量列車運行曲線的計算。

1 地鐵列車運行模式及運行曲線計算

1.1 地鐵列車的運行模式

地鐵列車的運行一般采用三種模式[1]:

(1) 牽引-勻速-制動模式。該模式下,列車平均速度最大,站間運行時間最短,因此稱其為最小運營模式。

(2) 牽引-勻速-惰行-制動模式。該模式能夠兼顧運行質量和操作可行性,適用于地鐵列車運行的場景,得到廣泛采用。因此,本文運行曲線的計算也是針對這種模式。

(3) 采用兩次或者兩次以上的惰行方式。該模式一般只應用在站間距離較長的情況,比較少用。

1.2 運行曲線的計算流程

考慮到線路的通過能力,計算時將采用允許的最大牽引力、最大制動力和巡航速度。計算列車運行曲線，實際上就是確定各個工況的轉換點。具體地,針對牽引—勻速—惰行—制動模式,牽引過程是指列車起動加速到巡航速度的過程,牽引過程終點也是巡航過程的起點。結合車輛、線路條件可推算出巡航起點。相似地,把制動過程看作列車從惰行終點減速到停車的過程,在確定惰行末端速度后,就可反推出制動起點；把惰行過程看作列車從巡航速度減速運行到惰行末端速度的過程,可推算出惰行起點。具體步驟如下:

(1) 確定列車惰行末端速度,計算列車制動距離,確定制動起點;

(2) 確定列車的最大允許速度,即巡航速度,計算列車的惰行距離,確定惰行起點;

(3) 計算列車的牽引距離,確定巡航起點;

(4) 計算整個過程的列車運行曲線,并計算能耗、總運行時間、舒適度、停車誤差等指標。

2 優(yōu)化模型與隔離小生境粒子群算法

2.1 列車運行曲線優(yōu)化模型建立

主要考慮列車的能耗、運行時間、舒適度及停車精度等4個指標。計算如下:

(1) 結合牽引特性,分區(qū)段計算能耗。在恒力矩區(qū)和自然特性區(qū),能耗為：

E=FSF

(1)

式中:

E——列車能耗；

F——列車作用力；

SF——列車對應的走行距離。

在恒功率區(qū),列車能耗計算采用式(2)：

E=PTP

(2)

式中:

P——功率;

TP——功率對應時間。

(2) 運行時間可看作是列車在各個速度數(shù)值上維持時間的累積。即：

(3)

式中:

vmax——列車最大速度；

t(v)——速度時間函數(shù)；

v——列車速度。

(3) 舒適度的計算采用式(4):

(4)

式中:

J——舒適度，J值越小,運行越舒適;

a——加速度；

t——時間。

(4) 停車精度的計算采用式(5):

Serror=1 454-S(Tz)

(5)

式中:

Serror——停車誤差；

S(T)——時間距離函數(shù)；

Tz——最終運行時間。

因此,綜合優(yōu)化目標函數(shù)為:

(6)

式中:

Tm,Em,Jm——分別為最小運營模式下的列車運行時間、能耗和乘客舒適度;

wt,we,wj,ws——分別為運行時間、能耗、舒適度、停車精度對應的權重;

Fi——綜合優(yōu)化目標函數(shù)，F(xiàn)i度量綜合運行質量,其值越小,表示偏離理想狀態(tài)的程度越小,列車運行效果越好。

約束條件主要有兩個:最大運行速度不能超過80 km/h(實際運行中允許不超過81 km/h);停車誤差不能超過25 cm。

綜上所述,優(yōu)化模型為:

(7)

2.2 隔離小生境粒子群算法

生物學中通過觀察自然界中物種的動態(tài)特性,發(fā)現(xiàn)生存習性相近的物種容易聚居到一起形成小生境。將小生境應用于粒子群算法(PSO),形成小生境粒子群算法(NPSO)。其核心思想是形成穩(wěn)定、多樣、平行的搜索空間(即子群),降低陷入局部極值的概率,得到全局最優(yōu)解。因此,子群的劃分至關重要。而模仿地理環(huán)境的隔離技術不僅能充分考慮粒子個體的特殊性,且原理簡單、易于實現(xiàn)，故本文采用隔離小生境粒子群算法(INPSO)優(yōu)化多目標模型。主要內容包括:

(1) 個體的初始化和子群的初始隔離。隨機產(chǎn)生N個代表惰行末端速度的初始個體,按照大小排序,將其均分入K個子群。

(2) 確定最優(yōu)值。調用已經(jīng)編寫的程序計算運行指標,即每個個體對應的T、E、J、Serror,再根據(jù)式(6)計算每個個體對應的Fi值。根據(jù)Fi,找出各個子群的最小值,確定子群最優(yōu)值和種群最優(yōu)值。

(3) 確定子群規(guī)模。子群的規(guī)模與子群中個體的Fi值有關。Fi值越小,個體越符合要求,進化的概率越大。因此在計算每個子群Fi的平均值后,求倒數(shù),按照該數(shù)值大小比例決定子群規(guī)模。同時,為了保護種群的多樣性,子群的規(guī)模應該在[Mmin,Mmax]之間。其中，Mmin表示最小維持規(guī)模,Mmax表示最大允許規(guī)模。當計算出的子群規(guī)模大于Mmax時,限制其為Mmax;當子群規(guī)模小于Mmin時,增補其到Mmin。

子群平均適應值的計算式為:

(8)

式中:

fa，k(g)——g代第k個子群Fi的平均值；

fk，i(g)——g代第k個子群中第i個個體的Fi值；

nk(g)——g代第k個子群的規(guī)模。

子群第g+1代第k個子群規(guī)模的計算式為:

(9)

(4)子群進化。個體的速度、位置更新為:

v′in=wvin+c1r1(pin-xin)+c2r2(pgn-xin)

(10)

x′in=xin+vin

(11)

式中:

xin——個體當前位置;

x′in——更新后位置；

vin——個體當前速度;

v′in——更新后速度；

w——慣性因子,表示粒子保持之前運動趨勢的能力;

c1——學習因子1,表示粒子向子群最優(yōu)值靠近的趨勢;

c2——學習因子2,表示粒子向種群最優(yōu)值靠近的趨勢;

r1,r2——隨機參數(shù)；

pin——子群最優(yōu)值;

pgn——全局最優(yōu)值。

(5) 進化判定。

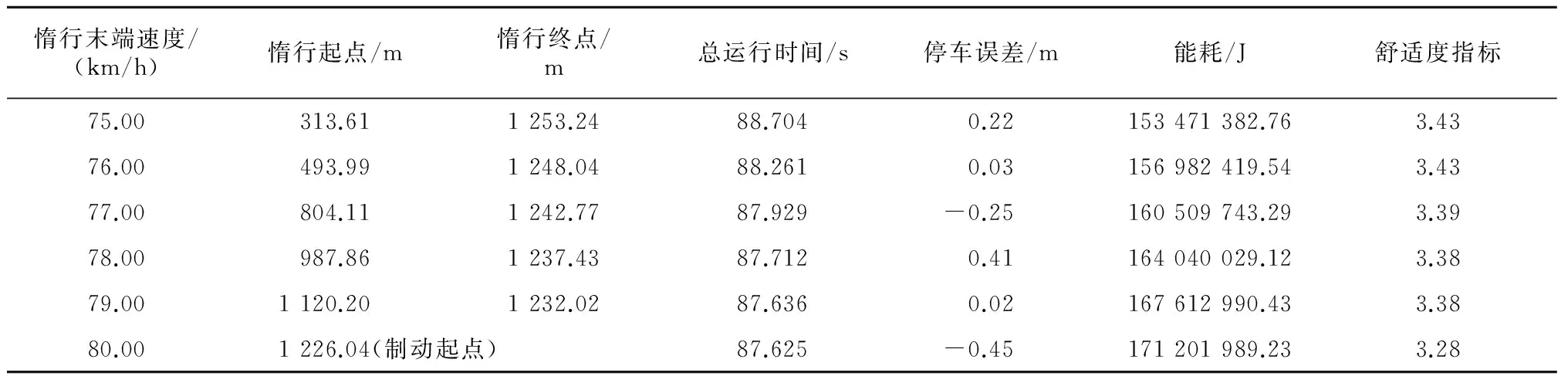
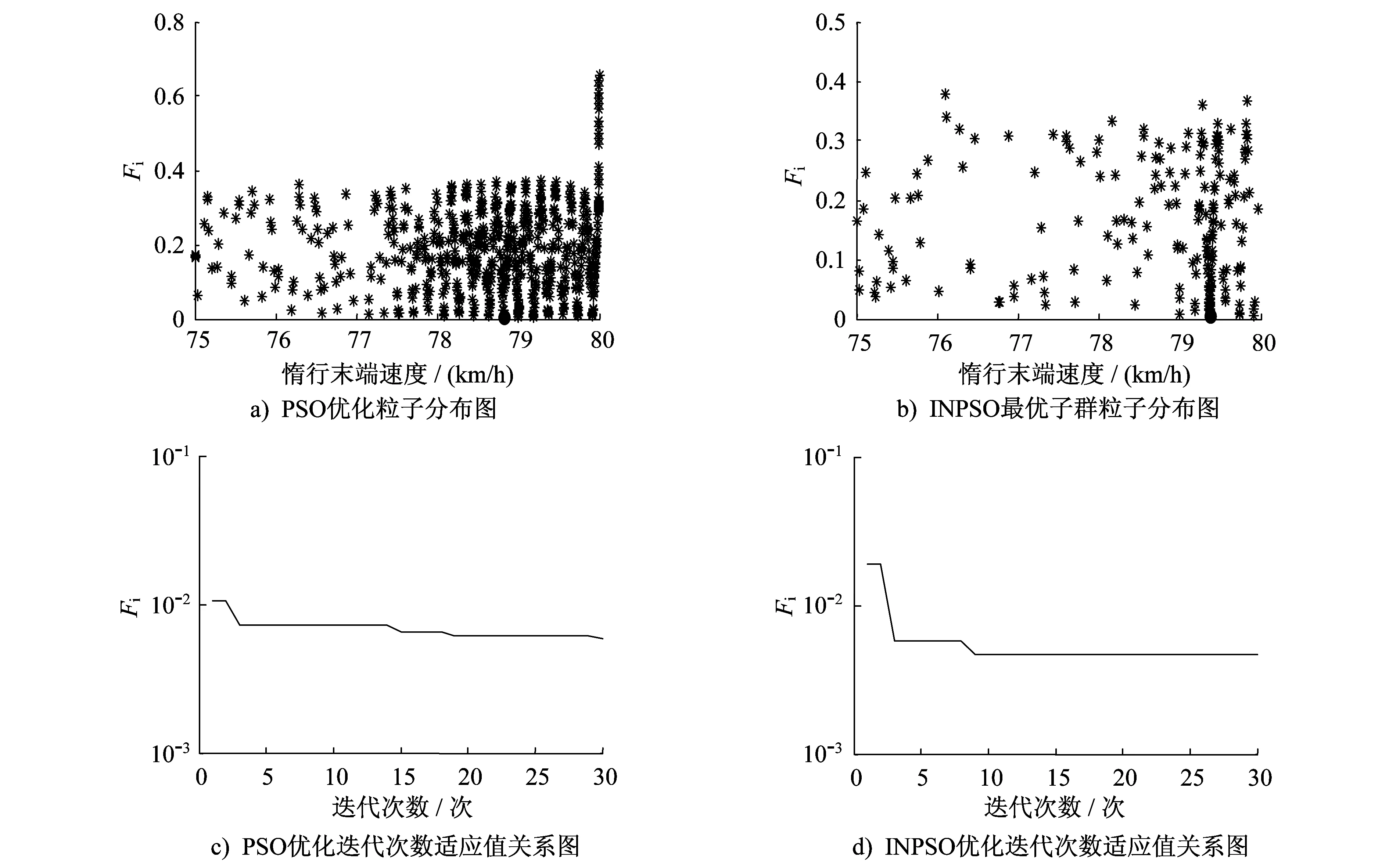
? 增補失效判定:當nk(g+1)

? 劣種不活判定:如果連續(xù)5代的規(guī)模均無法達到最小維持規(guī)模,則判定該子群無法適應,予以淘汰。由于粒子優(yōu)化區(qū)間不大,同時為了提高進化的效率,不再產(chǎn)生新子群替代。

? 進化遲滯判定:如果連續(xù)3個g值使得|fa,k(g)-fa,k(g-1)|<0.01成立,則判定該子群進化陷入停滯。保留已經(jīng)產(chǎn)生的最優(yōu)解,但不再產(chǎn)生新子群替代。

3 實例仿真

3.1 實例的選取

選取上海軌道交通2號線上海科技館站—世紀公園站的運行區(qū)間作為分析的實例。區(qū)間線路狀況如圖1所示。

注：斜杠以下數(shù)值為坡道長度，單位m；斜杠以上數(shù)值為坡度，單位‰

參考相關資料[3],上海軌道交通2號線采用AC02型電動列車，列車空車質量為220 t,滿載增為113.46 t,超載增為150 t；起動牽引力(起動階段列車速度從0上升到36 km/h)為387 kN；初始最大加速度(速度在0～36 km/h)為1.03 m/s2,最大減速度為1.12 m/s2。列車的加速過程特性為:速度在0～36 km/h為恒牽引加速;36～50 km/h為恒功率加速,牽引功率恒定;50～80 km/h以自然特性加速。

3.2 列車運行曲線計算程序的先驗知識

選取惰行末端速度分別為75 km/h、76 km/h、77 km/h、78 km/h、79 km/h、80 km/h,程序運行得到的列車運行指標如表1所示。在運行曲線中最大速度為80.00 km/h,巡航起點為249.87 m(以上海科技館站為坐標原點)。

表1 不同惰行末端速度對應的列車運行指標

3.3 優(yōu)化仿真結果分析

3.3.1 優(yōu)化參數(shù)設置

結合算法的特點,設置各權重系數(shù):W=[wtwewjws]=[0.1 0.1 0.1 0.7];迭代次數(shù)為30;PSO的初始粒子數(shù)目為25;INPSO子群個數(shù)為5,初始各子群粒子數(shù)目為5,Mmin=2,Mmax=10。

3.3.2 INPSO和PSO優(yōu)化對比

PSO和INPSO優(yōu)化結果對比如圖2及表2所示。觀察粒子分布可以發(fā)現(xiàn)，INPSO最優(yōu)子群迭代更集中在全局最優(yōu)解區(qū)域;比較迭代次數(shù)可知,INPSO能更快地收斂到最優(yōu)值。最重要的,如表2所示,在實際Fi值的優(yōu)化上,效果明顯,INPSO優(yōu)化結果僅為PSO優(yōu)化結果的58.96%。

綜上所述,INPSO算法在運行曲線的優(yōu)化尋優(yōu)上效果良好,可靠有效。

圖2 PSO和INPSO優(yōu)化結果對比圖

優(yōu)化結果惰行末端速度/(km/h)最優(yōu)Fi值實際可取結果惰行末端速度/(km/h)最優(yōu)Fi值PSO78.8179071476118480.00584425319157778.820.0134INPSO79.3693973962372470.00468409722530979.370.0079

3.3.3 最優(yōu)結果

綜合考慮各優(yōu)化指標的最優(yōu)惰行末端速度為79.37 km/h(對應的Fi值為0.007 9)。巡航起點在249.87 m處,惰行起點在1 159.86 m處,制動起點在1 230.02 m處;運行時間為87.619 s;停車誤差為0;耗能為1 689 404 483.64 J;舒適度指標為3.39。

對比文獻[3]中混合優(yōu)化的結果,INPSO實現(xiàn)了理想的停車精度,運行時間縮短了將近1 s,能耗較小，并且增加了舒適度指標,實現(xiàn)了列車的高質量運行。

4 結語

列車運行曲線的計算不僅關系著列車實時控制的精確實現(xiàn),也是運營管理部門估算運行成本、評估運行質量的重要資料。本文綜合考慮列車運行的能耗、舒適度、運行時間、停車誤差等運行指標,確定列車運行曲線的多目標優(yōu)化模型。鑒于隔離小生境粒子群算法克服局部極值的良好性能,利用該算法優(yōu)化模型,得到最優(yōu)的惰行末端速度,可實現(xiàn)列車高質量運行。仿真結果表明,隔離小生境粒子群算法尋優(yōu)可靠,效果顯著。

[1] 李歡.地鐵列車運行仿真及策略優(yōu)化[D].成都:西南交通大學,2012:37.

[2] 王勇博.采用遺傳算法優(yōu)化地鐵多區(qū)間速度曲線和停站時間實現(xiàn)牽引節(jié)能的仿真研究[D].南京:南京理工大學,2013:16.

[3] 李娜.城市軌道車輛運行節(jié)能方法優(yōu)化研究[D].上海:上海工程技術大學,2011:70.

[4] 余進,何正友,錢清泉.基于微粒群算法的多目標列車運行過程優(yōu)化[J].西南交通大學學報,2010,45(1):70.

[5] 康珉.移動閉塞條件下高速列車追蹤運行控制算法研究[D].長沙:中南大學,2013:26.

[6] 向長城,黃席樾,楊祖元.小生境粒子群優(yōu)化算法[J].計算機工程與應用,2007,43(15):41.

[7] 賈東立,張家樹.基于混沌變異的小生境粒子群算法[J].控制與決策,2007,22(1):117.

[8] 王甫,鄭亞平,劉天琪.一種基于調節(jié)因子的小生境粒子群優(yōu)化算法[J].計算機工程,2014,40(8):147.

[9] 黃平,于金揚,元泳泉.一種改進的小生境多目標粒子群優(yōu)化算法[J].計算機工程,2011,37(18):1.

[10] 宮林,王昕,劉斌.隔離小生境遺傳算法在配電網(wǎng)絡重構中的應用[J].電力系統(tǒng)及其自動化學報,2011,23(4):143.

[11] 馬松濤.復雜優(yōu)化問題中小生境粒子群優(yōu)化算法的改進及研究[D].鄭州:鄭州大學,2013:35.

Application of Isolation Niche Particle Swarm Optimization in Optimization of Subway Train Operation Curve

TIAN Zhipeng, MI Gensuo, WANG Baobao

Aiming at the extremely simple performance indexes of metro train operation optimization, a calculation flow of train operation curve with “traction-crusing-coasting-braking” mode is proposed, the energy consumption, passengers comfort, operation time, parking precision are taken into comprehensive consideration, the valueFiis used to comprehensively measure the operation quality (the smallerFimeans the closer to ideal state), and an optimization model is established. Combined with niche particle swarm optimization (INPSO) and isolation technology, the niche particle swarm optimization (INPSO) to be applied in optimization of train operation curve is designed. Then, based on an instance simulation, the model is optimized by IPSO, coasting terminal velocity is determined and the calculation of subway train optimum operation curve with high quality is completed. The valueFioptimized by INPSO is about 58.96% of the optimization result in basic particle warm algorithm, verifying the remarkable effect, the validity and reliability of INPSO.

metro; operation curve optimization; comprehensive operation quality; isolation niche particle swarm optimization

U 231.6

10.16037/j.1007-869x.2016.04.002

2015-05-02)