具有食餌避難所的Leslie-Gower捕食系統的捕獲分析
楊燕,趙 春
(天津師范大學數學科學學院,天津 300387)
具有食餌避難所的Leslie-Gower捕食系統的捕獲分析
楊燕,趙 春
(天津師范大學數學科學學院,天津 300387)
研究一類具有食餌避難所的Leslie-Gower捕食系統的捕獲問題.首先分析了系統平衡態的存在性和穩定性條件,然后獲得了經濟平衡點的存在性條件,并分析了避難所對經濟平衡點的影響,最后利用Pontryagin最大值原理得到了達到最優捕獲的最優平衡解.
Leslie-Gower捕食系統;食餌避難所;存在性;穩定性;平衡點;最優捕獲
種群動力學模型是描述種群與環境,種群之間相互競爭、相互作用的動力學關系的數學模型,用來預測、描述以及調節和控制物種的發展過程和發展趨勢.其中,Leslie-Gower模型[1]和Lotka-Volterra模型[2]是捕食者-食餌系統中2類重要模型.Leslie-Gower模型體現了環境對捕食者的承載能力與食餌的數量成正相關,比一般的Lotka-Volterra模型更具有實際意義.因此,許多學者對Leslie-Gower捕食者-食餌模型進行了深入研究并取得了許多成果.文獻[3]通過構造合適的Lyapunov函數證明了正平衡點的全局穩定性.文獻[4]對加入避難所的模型進行分析,發現避難所對系統的持久性不會產生影響.文獻[5]研究了具有捕獲項的Leslie-Gower模型,詳細分析了捕獲的作用,發現在某種條件下捕獲對食餌的平衡密度不產生影響,并得到達到最優捕獲的平衡解.文獻[6]對具有避難所的Leslie-Gower模型的最優稅收問題進行分析,得到了達到最優稅收量的最優平衡解.文獻[7]研究了具有食餌避難所和Michaelis-Menten項的Leslie-Gower模型,得到了平衡解穩定性的條件以及最優收獲的最優平衡解.文獻[8]研究了具有Holling型功能反應的最優捕獲策略.本研究考慮一類三種群捕食系統,將食餌種群(x)分為2部分,mx數量的食餌種群躲進避難所(0 其中:x(t)為食餌種群在t時刻的密度;y(t)、z(t)分別 為2個競爭捕食種群在t時刻的密度;r1、r2、r3分別為3個種群的內稟增長群;r1/a1>0為x種群的環境容納量;q1(1-m)>0、q2>0分別為對x、z種群的可捕系數;E1>0、E2>0分別為對食餌x與捕食者z進行收獲的努力量.為了避免過度捕獲,假設0<q1E1(1-m)<r1,0<q2E2<r3.根據x、y、z的生物意義,僅在區域R+= {(x,y,z)|x>0,y>0,z>0}內對系統(1)進行討論. 由0<q1E1(1-m)<r1,0<q2E2<r3,通過簡單計算得到正平衡點M(x*,y*,z*)存在,其中 顯然內部平衡點x*、y*、z*滿足下列方程組 定理1當ab-c>0時,正平衡點M(x*,y*,z*)局部漸近穩定,其中 證明 系統(1)在正平衡點 M(x*,y*,z*)處的Jacobi矩陣為 特征多項式為λ3+aλ2+bλ+c=0.顯然a>0,b>0,c>0,由Routh-Hurwitz判據可得結論成立. 定理2 正平衡點M(x*,y*,z*)是全局漸近穩定的. 證明 構造函數V(x,y,z) 易知V(x,y,z)是關于x、y、z的連續函數,計算得 因此,當x=x*,y=y*,z=z*時,系統取全局最小值,即 沿著系統(1)對V(x,y,z)求導 生物平衡點是系統(1)的平衡點,經濟平衡點則是當經濟利潤最大時所求的平衡點.假設捕獲x、z種群所需要的費用不變,分別用d1、d2表示,單位資源x、z的售價也為常數,分別用p1、p2表示.捕獲2種群可獲得的經濟利潤為 X1、X2分別為捕獲x、z種群所得的經濟利潤.如果p1q1·(1-m)x>d1,p2q2z>d2,即捕獲x、z種群所得的經濟利潤分別大于捕獲該種群所需要的費用,這時才對2種群進行捕獲. 定理3如果 則經濟平衡點(x1∞,y1∞,z1∞,E1∞,E2∞)存在. 證明 經濟平衡點由下列方程組確定 顯然當式(3)成立時,E1∞>0,E2∞>0.因此,經濟平衡點(x1∞,y1∞,z1∞,E1∞,E2∞)存在. 下面考慮避難所對經濟平衡點的影響,分2種情況討論:不能捕獲到避難所內的食餌種群和可以捕獲到避難所內的食餌種群. Ⅰ不能捕獲到避難所內的食餌種群.這時系統的經濟平衡點(x1∞,y1∞,z1∞,E1∞,E2∞)如定理3所述,且x1∞、y1∞、z1∞、E1∞、E2∞均是關于避難所m的連續可微函數,且 Ⅱ可以捕獲到避難所內的食餌種群.假設p1q1x>d1,p2q2z>d2.這時捕獲2種群所獲得的經濟利潤為 定理4如果 證明 經濟平衡點由下列方程組確定 在這種情況下,經營者可以捕獲到避難所內的x種群,即避難所的大小對可捕獲x種群的數量沒有影響,所以在經濟平衡時,x種群的密度不隨避難所的變化而變化,而避難所的增大,使y、z種群的競爭加大,表現為y種群密度隨著避難所的增大而減小.但是對于種群z而言,捕獲所獲得的利潤減少,經營者便減少對z種群的捕獲.2種作用力相互抵消,使得避難所的增大對z種群生物平衡不產生影響.隨著避難所的增大,捕獲x種群所獲得利潤有增大的趨勢,經營者便加大對x種群的捕獲,表現為增大;而捕獲z種群所獲得利潤減少,表現為減小. 捕獲者的目標是從資源開發中得到最大的凈利潤.考慮如下現值函數 其中δ為貼現率.本節通過確定最優捕獲量E1=E1δ,E2=E2δ,使得J在滿足狀態方程(1)和控制約束條件0≤Ei(t)≤(Ei)max(i=1,2)時取得最大值,此時控制問題的Hamilton函數為 其中λ1、λ2、λ3為伴隨變量.令 為轉換函數.使H取最大值的最優控制應滿足條件 當ψi(t)=0(i=1,2)時,Hamilton函數H與控制變量無關,即滿足此條件的控制為奇異控制.奇異控制滿足ψi(t)=0(i=1,2),即為 所以最優捕獲策略應滿足 下面尋求優化問題的最優平衡解,此時x、y、z、E1、E2均為常數,且滿足系統(1)和式(7)~式(11).下面結合求解伴隨方程(9)~方程(11). 由系統(1)可得 故式(12)和式(13)可表示為如下關于x、z的方程組 如果此方程組存在正實數根x=xδ,z=zδ,則可得 [1]LESLIE P H,GOWER J C.The properties of a stochastic model for the predator-prey type of interaction between species[J].Biometrica,1960,47(3):219-234. [2]陳婉琳,陳風德,王海娜,等.具有避難所的Lotka-Volterra競爭系統捕獲分析[J].應用數學學報,2014,6(37):1117-1129. CHEN W L,CHEN F D,WANG H N,et al.Harvesting analysis of a Lotka-Volterra competitive system incorporating a refuge[J].Acta MathematicaeApplicataeSinica,2014,6(37):1117-1129(inChinese). [3]KOROBEINIKOV A.A Lyapunov function for Leslie-Gower predatorprey models[J].Applied Mathematics Letters,2001,14(6):697-699. [4]CHEN F D,CHEN L J,XIE X D.On a Leslie-Gower predator model incorporating a prey refuge[J].Nonlinear Analysis:Real World Applications,2009,10(5):2905-2908. [5]ZHANG N,CHEN F D,SU Q Q,et al.Dynamic behaviors of a harvesting Leslie-Gower predator-prey model[J].Discrete Dynamics in Nature&Society,2011,43(1):309-323. [6]李有文,楊洪嫻,田廣立,等.具有食餌避難的Leslie-Gower最優稅收模型分析[J].數學的實踐與認識,2011,5(41):238-243. LI Y W,YANG H X,TIAN G L,et al.Analysis of a harvested Leslie-Gower predator-prey model through optimal taxation[J].Mathematics in Practice and Theory,2011,5(41):238-243(in Chinese). [7]GUPTA R P,BANERJEE M,CHANDRA P.Bifurcation analysis and control of Leslie-Gower predator-prey model with Michaelis-Menten type prey-harvesting[J].Differ Equ Dyn Syst,2012,20(6):339-366. [8]李雅芝,竇家維.一類3種群系統的動力學行為及優化問題研究[J].西南大學學報:自然科學版,2014,7(36):73-78. LI Y Z,DOU J W.Dynamics and optimization of a three-population system[J].Journal of Southwest University:Natural Science Edition,2014,7(36):73-78(in Chinese). (責任編校 馬新光) Harvesting analysis of a Leslie-Gower predator-prey system with prey refuge YANG Yan,ZHAO Chun The harvesting problem for a Leslie-Gower predator-prey system with prey refuge is studied.Firstly,the existence and stability of equilibrium states are analyzed.And then the existence of the equilibrium point is obtained,and the effect of the refuge on the equilibrium point is analyzed.Finally,the optimal harvesting policy is obtained by using the Pontryagin′s maximum principle. Leslie-Gower predator-prey system;prey refuge;existence;stability;equilibrium point;optimal harvesting O175 A 1671-1114(2016)04-0001-05 2015-12-08 國家自然科學基金資助項目(60972089). 楊 燕(1991—),女,碩士研究生. 趙 春(1963—),男,教授,主要從事控制論及其應用方面的研究.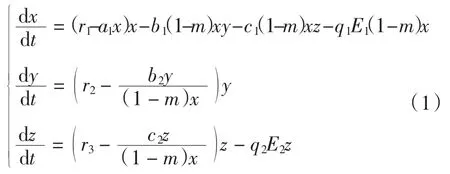
1 正平衡點的存在性和穩定性
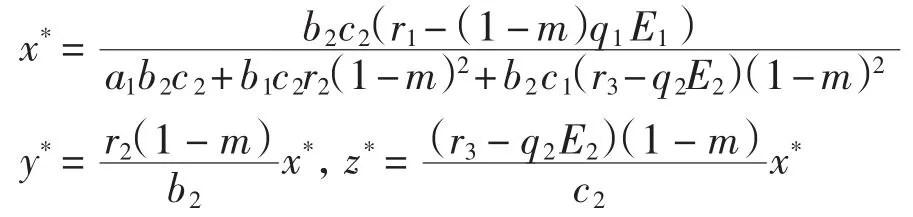
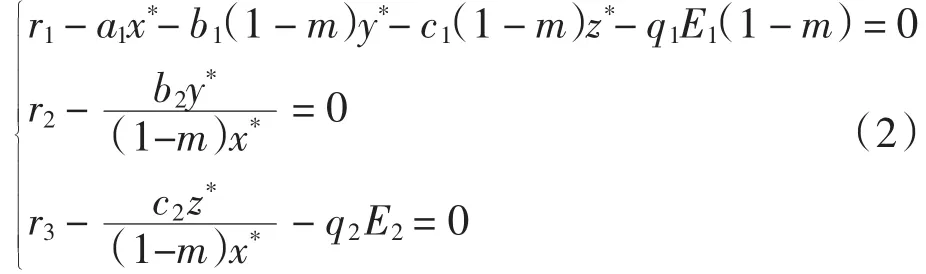
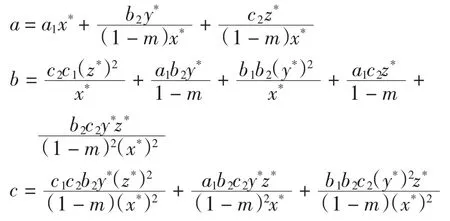
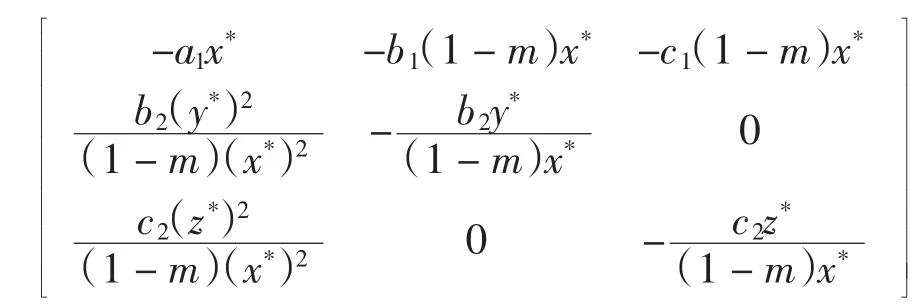
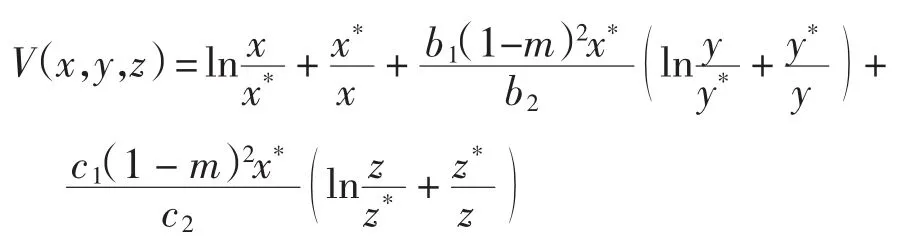

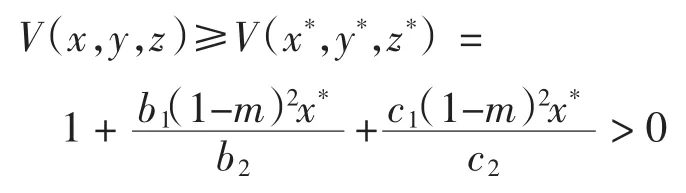
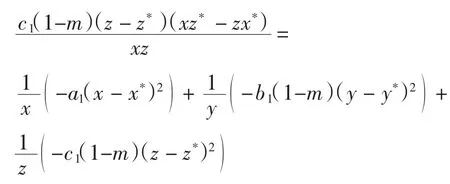
2 經濟平衡點
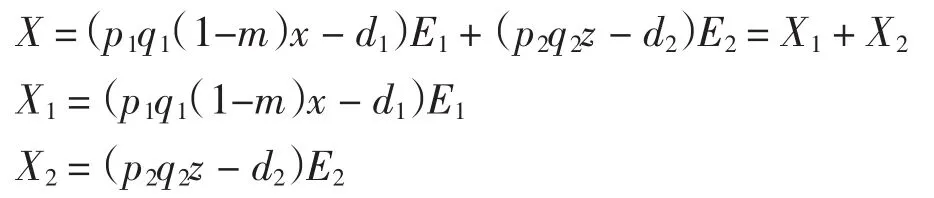
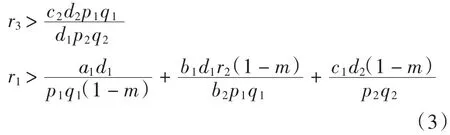
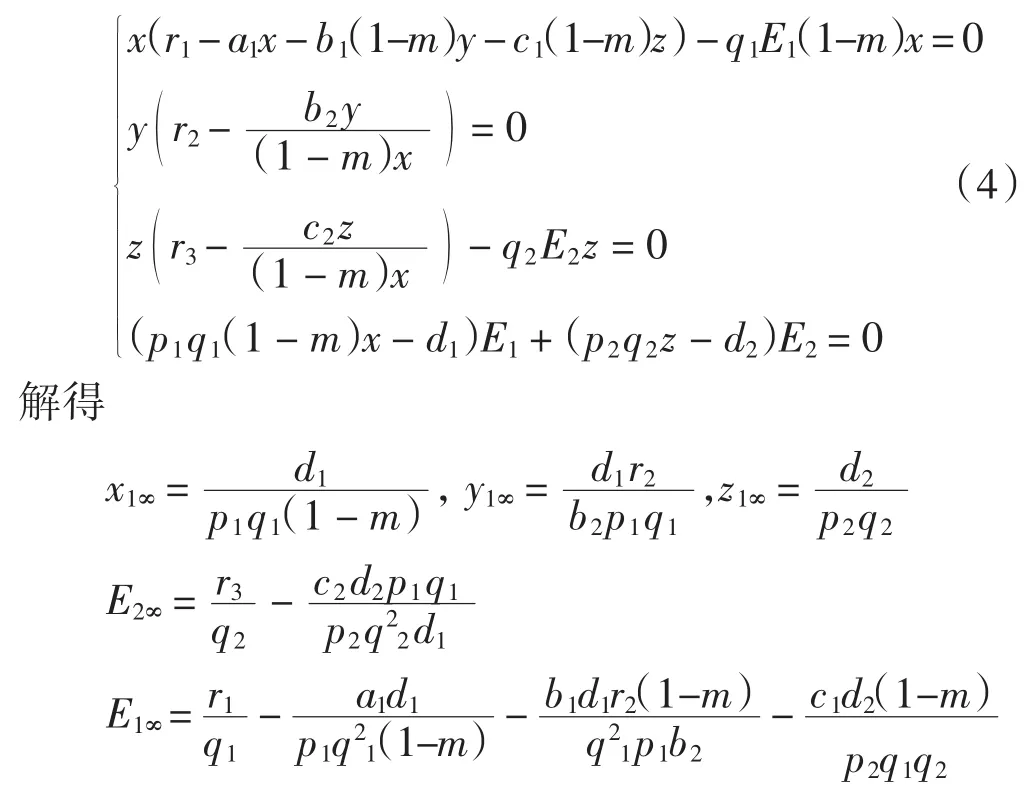
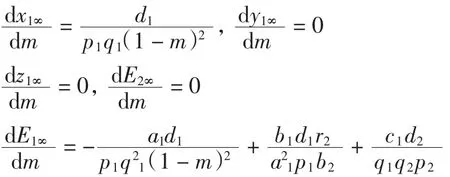
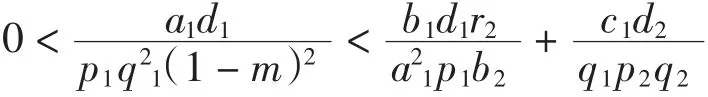

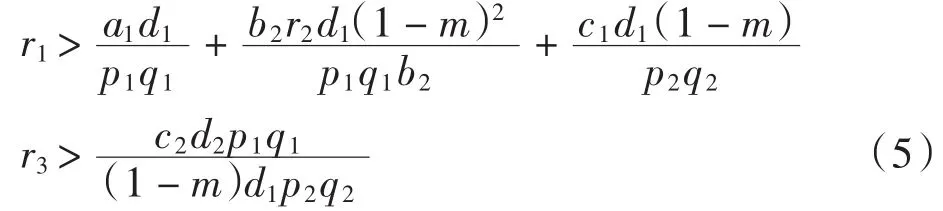
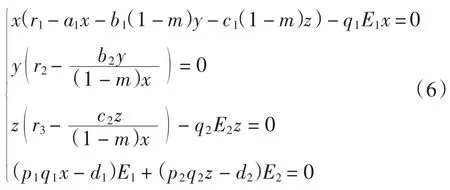
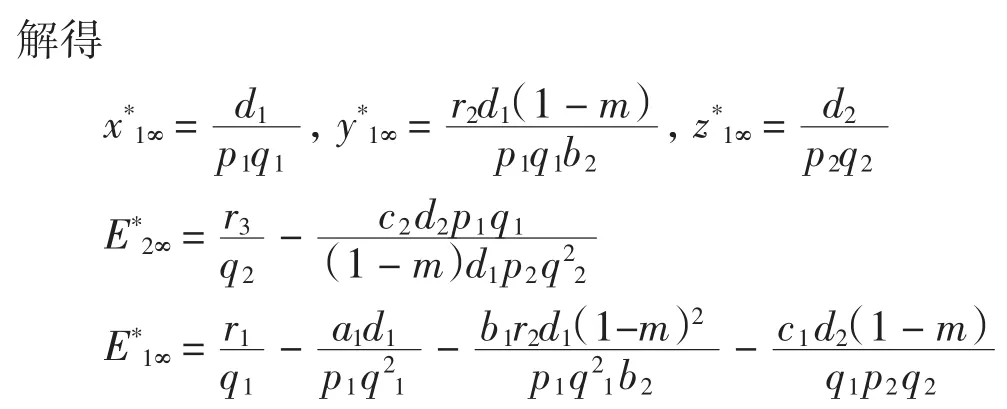
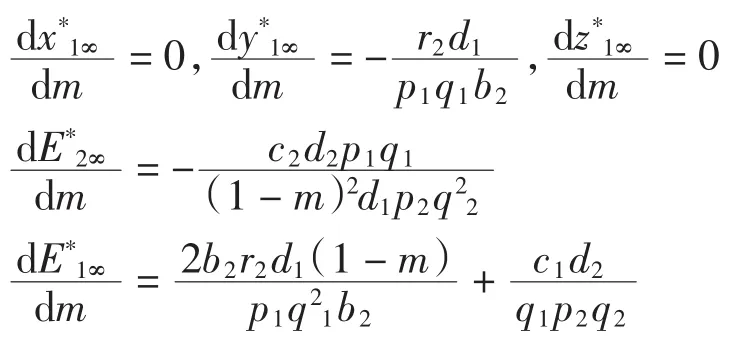
3 最優捕獲策略
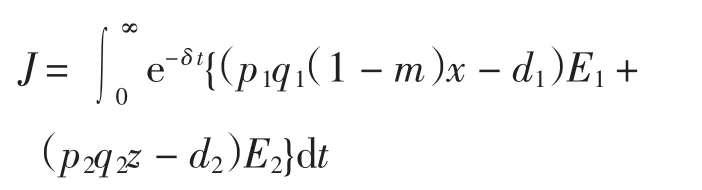
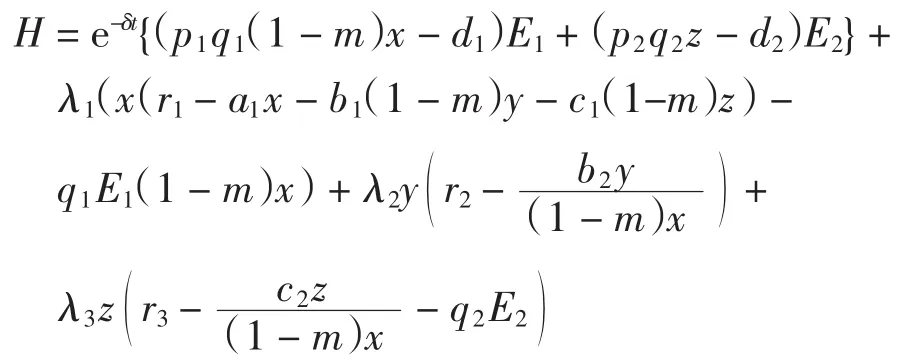
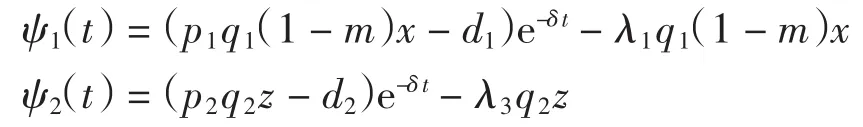
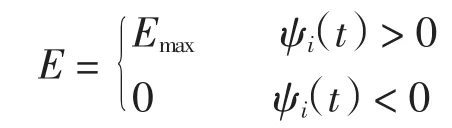
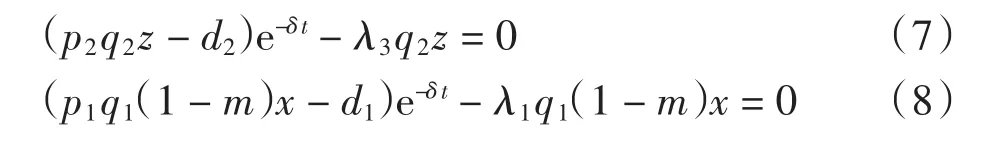


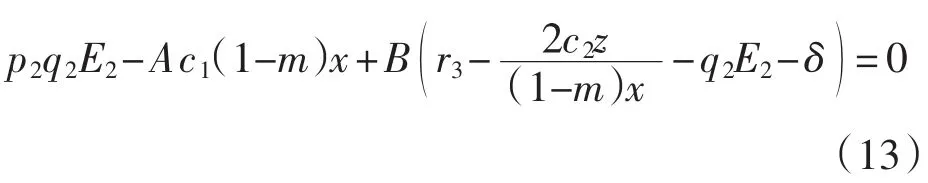
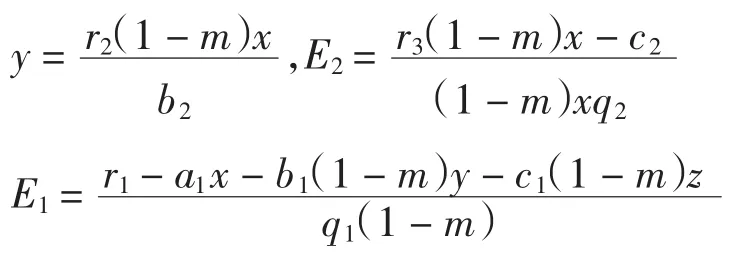
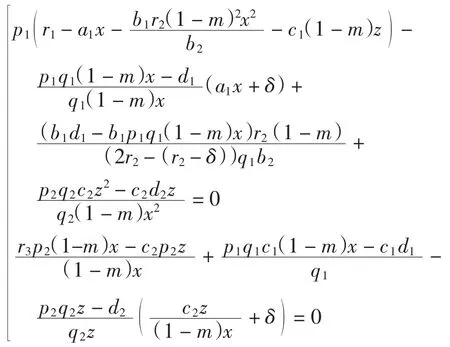
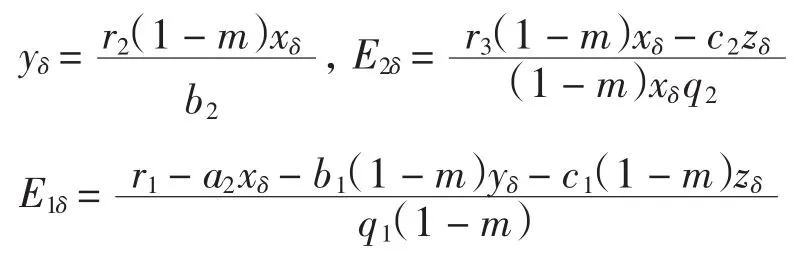
(College of Mathematical Science,Tianjin Normal University,Tianjin 300387,China)

