羅爾定理的推廣及其應用

趙凌燕，李寶毅

（天津師范大學數學科學學院，天津300387）

羅爾定理的推廣及其應用

趙凌燕，李寶毅

（天津師范大學數學科學學院，天津300387）

基于羅爾定理，研究2種函數零點個數上界的問題.對于第1種函數，利用導函數的性質確定了不含間斷點的函數零點個數的上界，進而確定了含間斷點的函數零點個數的上界.對于第2種函數，利用函數滿足的微分方程的特征確定了函數零點個數的上界.

羅爾定理；零點個數；零點重數；間斷點

羅爾定理反映了函數與導函數之間的內在聯系，對函數零點個數的研究有重要意義.許多學者對羅爾定理的推廣進行了研究，這些結果主要可分為2類：第1類為通過函數性質估計導數零點個數的下界；第2類為通過導數性質估計原函數零點個數的上界.第1類推廣較為常見[1-4]，第2類推廣相對較少[5-6]，而第2類推廣對常微分方程極限環個數的研究具有重要意義[7-8].本研究考慮羅爾定理的第2類推廣形式，得到2種函數零點個數的上界.本研究是在原有的羅爾定理推廣上再次進行推廣，對常微分方程極限環個數的確定有重要幫助.

下面的引理是本研究羅爾定理推廣形式的基礎.

引理1[6]設函數f（x）在閉區間[a，b]上連續可導.

（1）若f(n)（x）存在且在開區間（a，b）內有k個零點（不計重數），則f（x）在閉區間[a，b]上最多有n+k個零點（不計重數）.

（2）若f(n)（x）存在且在開區間（a，b）內有k個零點（計重數），則f（x）在開區間（a，b）內最多有n+k個零點（計重數）.

推論 設函數f（x）是定義在閉區間[a，b]上的函數，f（x）在開區間（a，b）內有s個間斷點，且f（x）在非間斷點處連續可導.

（1）若f(n)（x）在開區間（a，b）內有k個零點（不計重數），則f（x）在閉區間[a，b]上除間斷點外最多有（s+ 1）n+k個零點（不計重數）.

（2）若f(n)（x）在開區間（a，b）內有k個零點（計重數），則f（x）在開區間（a，b）內除間斷點外最多有（s+ 1）n+k個零點（計重數）.

記P(n)（x）為關于x的n次多項式，deg0=-1，#f為函數f（x）的零點個數（計重數）.

1 羅爾定理的推廣形式I

引理4 設a≠b，a?Z，對于非負整數n、k，若0≤k≤n，則

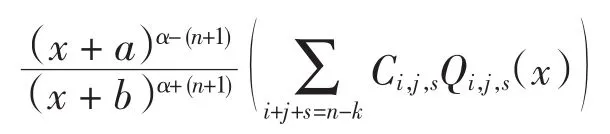
其中：Ci，j，s是關于i、j與s的函數，Qi，j，s（x）=（P(k)（x））(i)·（x+a）n-k-j（x+b）n-k-s，deg（P(k)（x））(i)=k-i，degQi，j，s（x）=（k-i）+（n-k-j）+（n-k-s）=n.

記Q(n)（x）=Qi，j，s（x），則有

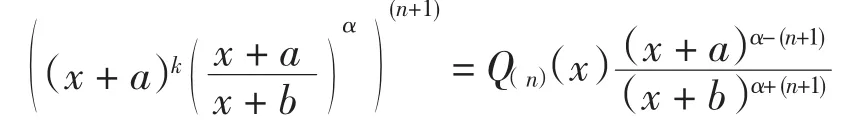
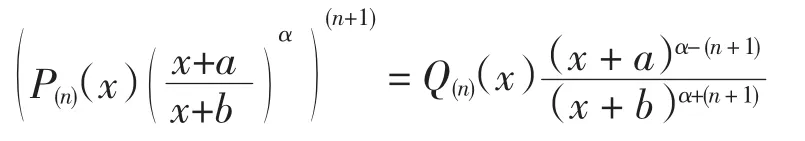
證明 設P(n)（x）=anxn+an-1xn-1+…+a1x+a0，an≠0.利用函數在x=a處的泰勒展開式以及引理4即可得結論成立.

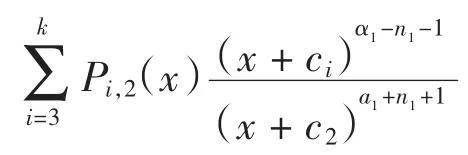
#f≤（n0+1）+（k-1）（n1+1）+n1=k+n0+kn1

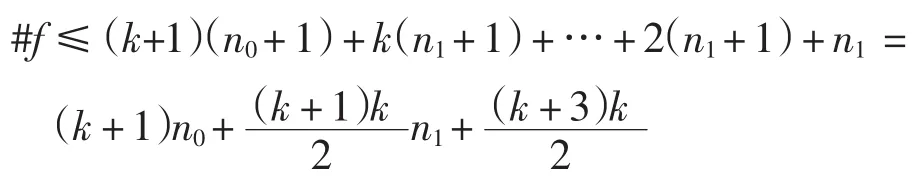
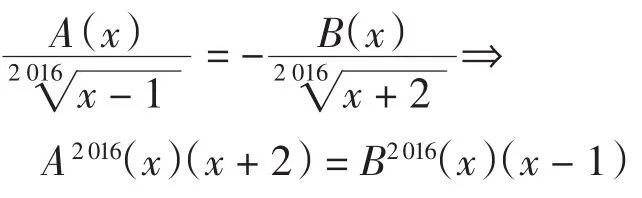
x的最高次冪指數是20 161，則函數f（x）零點個數不超過20 161.根據定理1，，k=2，n0=-1， n1=10，故f（x）的零點個數不超過21.

由該例可以看出，定理1可以大幅減小函數零點個數上界的估計值.

2 羅爾定理的推廣形式II

（a）P（x）在閉區間[a，b]上連續，在開區間（a，b）內可導.

（b）A（x）與B（x）在閉區間[a，b]上連續，F（x，P）在[a，b]×[mp，Mp]上連續，其中[mp，Mp]是P（x）在[a，b]上的值域.

則有以下結論成立

（1）若A（x）與B（x）在開區間（a，b）內分別有u*（u*∈N）個和v*（v*∈N）個零點（不計重數），則函數

定理2 設系統P（x）在閉區間[a，b]上至多有u*+v*+1個零點（不計重數）.

（2）若A（x）與B（x）在開區間（a，b）內分別有u（u∈N）個和v（v∈N）個零點（計重數），則函數P（x）在開區間（a，b）內至多有u+v+1個零點（計重數）.

證明 （1）設P（x）在閉區間[a，b]上有k*個零點x*i（1≤i≤k*），且a≤x*1＜x*2＜…＜x*k*≤b.

當B（x*i+1）=0時，則結論顯然成立.

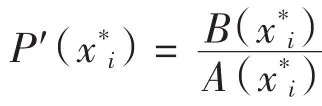
當B（x*i+1）≠0且B（x*i）=0時，設x*i是B（x）=0的βi次重根，B（x）=（x-x*i）βiB*（x），則必有B*（x*i+0）· B（x*i+1）＜0，否則B*（x*i+0）B（x*i+1）＞0.由P′（x*i）=，可知P′（x*i+0）P′（x*i+1）＞0，由前述證明過程知P（x）在（x*i，x*i+1]內至少有1個零點，這與x*i、x*i+1是相鄰2個零點矛盾.則B*（x*i+0）B（x*i+1）＜0，B（x）在（x*i，x*i+1]內至少有1個零點.

綜上可知，P（x）的零點的個數k*與B（x）的零點個數v*滿足：k*-1≤v*，即k*≤v*+1.

②若A（x）在閉區間[a，b]上有零點，下面證明A（x）或B（x）在（x*i，x*i+1]內至少有1個零點.

若A（x）在[x*i，x*i+1]上沒有零點，則由前面討論可知B（x）在（x*i，x*i+1]內至少有1個零點.

若A（x）在（x*i，x*i+1]內有零點，即存在c∈（x*i，x*i+1]，使得A（c）=0，結論顯然成立.

若A（x*i）=0且A（x）在（x*i，x*i+1]內沒有零點，則F（x*i，P）P（x*i）+B（x*i）=0，即B（x*i）=0，在（x*i-1，x*i]∪（x*i，x*i+1]上至少存在A（x）或B（x）的2個零點.

綜上可知，A（x）、B（x）和P（x）的零點個數u*、v*

和k*滿足k*≤u*+v*+1.

（2）設P（x）在（a，b）內有n個零點xi（1≤i≤n），且滿足a＜x1＜x2＜…＜xn＜b，其重數分別是k1，k2，…，kn，且k1+k2+…+kn=k.

在點xi（1≤i≤n）處，xi是P（x）的ki次重根.由 B（x）=F（x，P）P（x）-A（x）可知，xi是P（x）的至少ki-1次重根.下面證明A（x）或B（x）在（xi，xi+1）內至少有1個零點.

當A（x）在（xi，xi+1）內有零點時，結論顯然成立.

當A（x）在（xi，xi+1）內沒有零點且A（xi）=0時，由A（x）=F（x，P）P（x）+B（x），可知B（x）i=-F（xi，P（x）i）·P（xi），則xi是B（x）的至少ki次重根.此時可看作在（xi-1，xi）與（xi，xi+1）內共有A（x）和B（x）的2個零點.

當A（x）在[xi，xi+1]內沒有零點時，不妨設A（x）＞0（x∈[xi，xi+1]）恒成立，則必有B（xi+0）B（xi+1-0）＜0.否則B（xi+0）B（xi+1-0）＞0，由

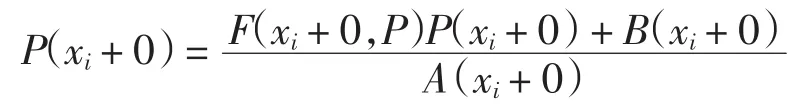
可知P′（xi+0）P′（xi+1-0）＞0，則有P′（xi+0）＞0，P′（xi+1-0）＞0或P′（xi+0）＜0，P′（xi+1-0）＜0.對這2種情況，由連續函數介值存在定理可知，在（xi，xi+1）內必存在P（x）的1個零點，與（xi，xi+1）內無零點矛盾.所以B（xi+ 0）B（xi+1-0）＜0，在（xi，xi+1）內存在B（x）的1個零點.

例2 考慮函數f（x）=A（x）eB(x)+C（x）的零點個數，其中：A（x）、B（x）和C（x）是關于x的多項式，由f′（x）=A′（x）eB(x)+A（x）eB(x)B′（x）+C′（x）得

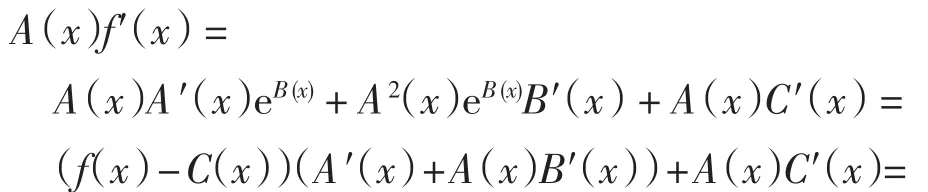
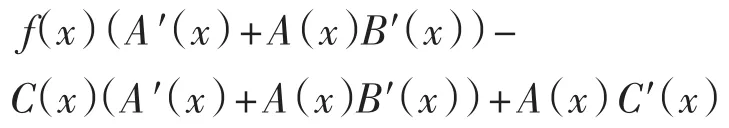
根據定理2，f（x）零點個數不超過

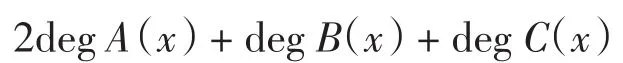
[1]汪軍.廣義羅爾定理及其應用實例[J]．遼寧工程技術大學學報：自然科學版，2000，19（1）：93-94．WANG J.The generalized Rolle Theorem and its applied example[J]. Journal of Liaoning Technical University：Natural Science，2000，19（1）：93-94（in Chinese）．

[2]劉艷，姚邵義.羅爾定理的推廣形式[J].天津師范大學學報：自然科學版，2005，25（2）：45-46. LIU Y，YAO S Y.On the generalization of Rolle Theorem[J].Journal of Tianjin Normal University：Natural Science Edition，2005，25（2）：45-46（in Chinese）.

[3]劉曉玲，閆峰.羅爾定理的三種推廣形式[J].高等數學研究，2011，14（5）：7-8. LIU X L，YAN F.Three generalizations of Rolle Theorem[J].Studies in College Mathematics，2011，14（5）：7-8（in Chinese）.

[4]惠菊梅.羅爾定理的推廣形式及應用再討論[J].青海大學學報：自然科學版，2007，25（5）：82-84．HUI J M.Generalizations of Rolle Theorem and re-discussion of its application[J].Journal of Qinghai University：Natural Science，2007，25（5）：82-84（in Chinese）．

[5]GASULL A，ILIEV D.Two-dimensional Fuchsian systems and the Chebyshev property[J].Journal of Differential Equations，2003，191：105-120.

[6]段敏敏.一類五次Hamilton系統Abel積分零點個數上界的估計[D].天津：天津師范大學，2014. DUAN M M.Estimation of upper bound of number of zeros for Abelian integrals of a kind of quintic Hamiltonian system[D].Tianjin：Tianjin Normal University，2014（in Chinese）.

[7]WANG J.Estimate of the number of zeros of Abelian integrals for a perturbation of hyperelliptic Hamiltonian system with nilpotent center[J]. Chaos Solitons Fractals，2012，45：1140-1146.

[8]ASHEGHI R，ZANGENEH H R Z，ATABAIGI A.On the number of limit cycles in small perturbations of a class of hyper-elliptic Hamiltonian systems[J].Nonlinear Analysis，2012，75：574-587.

（責任編校 馬新光）

Promotion of Rolle Theorem and it's application

ZHAO Lingyan，LI Baoyi
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

On the basis of Rolle Theorem，the upper bounds of numbers of zeros for two kinds of functions are studied.For the first kind，the upper bound of zeros for the functions without discontinuities is determined by using the properties of derived functions，and then the upper bound of zeros for the functions with discontinuities is given.For the second kind，the upper bound of zeros is determined by using the features of the differential equation for the functions.

Rolle Theorem；number of zeros；zero multiplicity；discontinuities

O175.1

A

1671-1114（2016）03-0006-04

2015-09-30

國家自然科學基金資助項目（11271046）；天津師范大學博士基金資助項目（52XB1414）.

趙凌燕（1993—），女，碩士研究生.

李寶毅（1963—），男，教授，主要從事常微分方程定性理論及其應用方面的研究.