一類圖的彩虹連通數緊的上界的FPT算法

鄧興超

（天津師范大學數學科學學院，天津 300387）

一類圖的彩虹連通數緊的上界的FPT算法

鄧興超

（天津師范大學數學科學學院，天津 300387）

基于divide-and-conquer模式，針對有界樹寬度的圖設計了一個FPT算法，計算其彩虹連通數緊的上界，該算法是多項式時間可解的.

彩虹連通數；divide-and-conquer模式；FPT算法；樹寬度

Chartrand等[1]于2008年提出了圖的彩虹連通的概念.G=（V（G），E（G））是簡單有限連通圖，給圖G一個邊著色c:E（G）→{1，2，…，n}，n∈N，相鄰邊可能著同樣的顏色.若圖G的某條路上的邊著不同的顏色，則稱這條路為圖G的一條彩虹路.如果圖G的任意2個點都有一條彩虹路連接，則稱圖G為彩虹連通的，使得圖G為彩虹連通的最少的顏色數稱為G的彩虹連通數，記為rc（G）.如果圖G的任意2個點都有一條長度為其在G中距離的彩虹路連接，則稱圖G為強彩虹連通的，使得圖G為強彩虹連通的最少的顏色數稱為G的強彩虹連通數，記為src（G）.顯然有，其中diam（G）為圖G的直徑.彩虹連通是組合數學中刻畫圖連通性的連通度概念的一種自然推廣.文獻[2]證明了對于圖G，判斷是否rc（G）=2是NP-complete，并且計算rc（G）是NP-hard.文獻[3]證明了對于任意的k∈N，判斷rc（G）是否小于等于k是NP-hard；即使對二部圖判斷src（G）是否小于等于k也是NP-hard.一般圖是NP-hard的優化問題，對滿足某些條件的圖類或特殊圖類是具有多項式時間算法的.文獻[4]得到了包含三角的線圖的彩虹連通數，并給出了2類線圖的彩虹連通數的緊的上界；文獻[5]對極大外平面圖給出了計算其彩虹連通數緊的上界的多項式時間算法.

divide-and-conquer方法是一種算法設計模式，其思想就是把問題分解為一些子問題，而這些子問題可以用遞歸的方法求解，利用這些子問題的解可以求出原問題的解.這個方法在子問題比原問題在本質上小很多的時候是非常有效的.本研究基于divide-andconquer方法對有界樹寬度的圖設計一個FPT算法，計算其彩虹連通數緊的上界.

首先給出圖彩虹連通數的一個重要性質，即如下命題，它在本研究主要結果的證明中起到了決定性的作用.

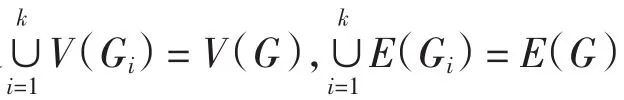
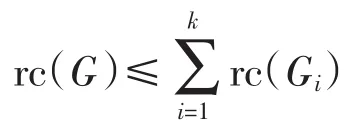
證明：對k用歸納法來證明此命題.當k=1時命題顯然成立.

假設結論對任意的k＜m（m≥2）成立.下面證明結論對k=m成立.

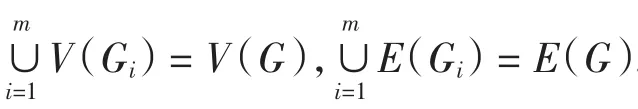
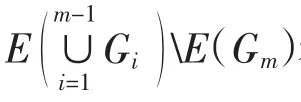
下面證明c是圖G的彩虹著色，進而說明命題結論對k=m成立.分3種情形證明對任給的2點x、y∈V（G），在著色方案c下有彩虹路連接它們.

情形1 對于任給的x、y∈V（Gm），顯然在Gm的c2著色下有一條彩虹路連接x和y.

情形2 任給2點x、y，x∈V（Gm），y∈V（G）V（Gm）.

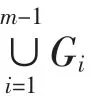
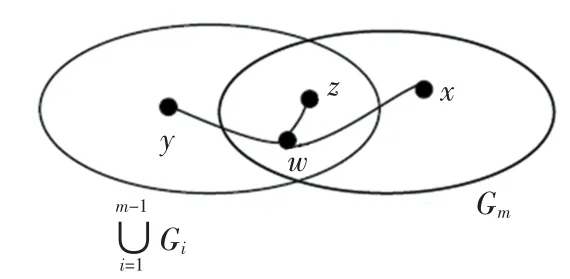
圖1 情形2（ii）Fig.1 Situation 2（ii）

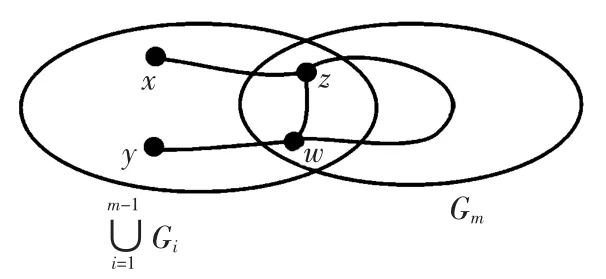
圖2 情形3（ii）Fig.2 Situation 3（ii）

定義 圖G=（V，E）的分解樹是一個二元對：

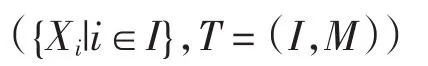
這里：Xi，i∈I為V的子集，T是頂點集為I邊集為M的一棵樹，滿足

（2）如果（u，v）∈E，則?i∈I，使得u、v∈Xi.

（3）對于所有的頂點v∈V，{i∈I|v∈Xi}可以導出一個T的連通子樹.

（4）如果i、k、j∈I，并且j在T的從i到k的路上，則Xi∩Xk?Xj.

1）、系列平行圖（Tw=2）、外平面圖（Tw=2）、Halin graphs（Tw=3）等.

定理1[6]任何一個具有n個點的圖G的非冗余分解樹最多有n個塊.

定理2[7]對任意給定的整數k和圖G，n=|V（G）|，則存在運行時間為O（2Θ(k3)n）的算法，判斷是否Tw（G）≤k，若是，則給出G的一個Tw（G）≤k的樹分解.

彩虹路問題（RPP）可描述為：

輸入：連通圖G，頂點r∈V（G），含l個顏色的圖G的一個著色方案cl.

輸出：對任給的v∈V（G），找到從r到v（若存在）所有的彩虹路.

設Qv表示cl著色下從r到v所有彩虹路的顏色序列的集合（如果存在），用qv表示Qv的元素，定義yv為cl著色下從r到v的彩虹路的長度，yv是從Qv到{1，…，l}的一個函數Yv=yv（Qv）.設p是彩虹路的前繼函數，對任給的一條彩虹路qv的任一點，p給出其前繼點.初始化Yv和p意味著設定yr=φ，p（r）=0，qr=φ，qv=φ，yv=l+1，并且對于任意v∈V{r}，有p（v）=-1.綜上，解決RPP問題的彩虹路算法（RPA）流程如下：

（1）對于任意一個v∈V（G），初始化Yv、Qv、p.

（2）對于任意一個vi∈V（G），有Yvi、Qvi和p.如果vi有關聯邊（vi，w），并且其顏色與qvi∈Qvi的顏色不同，則延伸qvi，得到新的彩虹路顏色序列qw=qvi∪{（viw）的顏色}.

下面通過一個例子說明上述RPA算法的有效性.給定一個具有8著色且1個頂點r的圖G，見圖3.

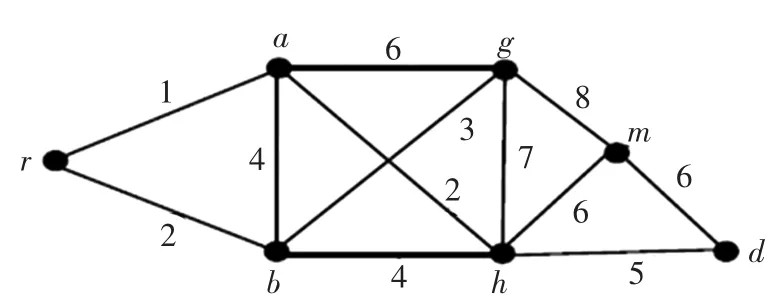
圖3 具有8著色且1個頂點的圖GFig.3 Graph G with 8-coloring and 1 vertex

RPA的運行結果見表1.由表1可得，用此算法檢驗圖G的邊，考慮RPA算法中r，m-彩虹路對應的參數變化.由m行可得，m有3個前繼點，并且有14條彩虹路連接r和m；接著看到m行hm列，第2個顏色序列是246；然后考慮h行，找到相同的顏色序列24；接著看到h行ab列，h的前一個節點是b.通過同樣的程序，可得b的前繼頂點是r.因此，找到彩虹路rbhm.另外的13條彩虹路也可以通過同樣的方式得到.對于任意v∈V（G），所有連接r、v的彩虹路也可以通過同樣的方法獲得.因為G最多有|V（G）|（|V（G）|-1）/2條邊，所以RPA算法在有限時間內是可以結束的.

表1 RPA的輸出結果Tab.1 Output results of RPA

引理1 對于任意具有|V（G）|=k+1個點的圖G，且G具有用l個顏色的邊著色cl，則存在對于邊著色cl的蠻力算法，可以得到所有的從r到v的彩虹路（如果存在），對于任意的v∈V（G），算法運行時間不大于g（k，l）=k（l+2k-1l！）.

證明 因為著色方式cl用l種顏色，對于任意的v∈V（G），任意連接r和v的彩虹路長度小于等于l.對任給頂點v∈V（G），連接r和v的i-長度路有i-1個其他點，于是最多需要

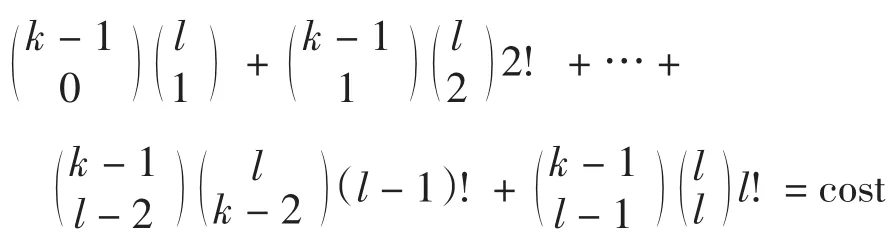
條邊來檢驗.從而易得

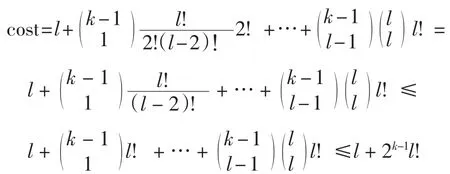
因此，運行時間最多不超過g（k，l）=k（l+2k-1l!）.

引理2 若|V（G）|=k+1，則可以通過蠻力算法計算圖G的彩虹連通數rc（G），其運行時間最多不超

過f（k）=k2（k+1）（k+2k-1k!）.

證明 為了給圖G彩虹著色，給圖G的一個生成樹的邊染成不同的顏色，顯然k是rc（G）的一個上界，僅考慮1≤l≤k條件下圖G的蠻力計算方法.這樣，計算rc（G）的運行時間最多不超過

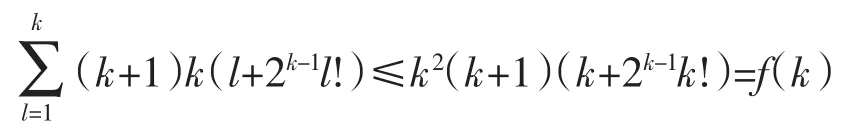
定理3 若G是樹寬度為k的簡單圖，則存在線性時間算法計算圖G的彩虹連通數的一個上界，計算所用時間不超過

證明 如果G是一個樹寬度為k的簡單連通圖，f（·）是一個增函數，于是由引理2，對圖G的分解樹的每一個塊，用蠻力算法計算每一個塊的彩虹連通數，其運行時間最多是f（k）.由命題和定理1，對樹寬度為k的圖G，可以在f（k）時間內計算rc（G）的一個上界.因此，結合定理2，對于任給的簡單連通圖G，都存在線性時間算法，此算法取決于Tw（G）是否小于等于k，如果可以得到圖G的一個分解樹滿足Tw（G）≤k，則可以計算rc（G）的一個上界，算法運行時間最多不超過

下面說明本研究算法給出的rc（G）的上界是緊的.圖4（b）是由n個圖4（a）構造而成的，其直徑為2n，樹寬度為2.利用本研究算法得到圖4（b）的彩虹連通數的一個上界是2n，顯然2n是圖4（b）的彩虹連通數.

圖4 diam（G）=2n，Tw（G）=2，rc（G）=2nFig.4 diam（G）=2n，Tw（G）=2，rc（G）=2n

下面總結本研究關于計算簡單連通圖彩虹連通數緊上界的算法：

輸入：圖G和整數k.

輸出：rc（G）的上界.

第1步：利用Bodlaender算法找樹寬度不超過k的圖G的分解樹（如果存在）.

第2步：對圖G的分解樹的每個塊利用RPA算法計算其彩虹連通數.

第3步：用命題和定理3獲得圖G的彩虹連通數rc（G）的上界.

注 本研究算法對于強彩虹連通數是無效的，因為在決定整個圖的彩虹連通數時測地距離是無法判斷的.

[1]CHARTRAND G，JOHNS G L，MCKEON K A.Rainbow connection in graphs[J].Math Bohemica，2008，133：85-98.

[2]CHAKRABORTY S，FISCHER E，MATSLIAH A，et al.Hardness and algorithms for rainbow connectivity[J].J Comb Optim，2011，21（3）：330-347.

[3]ANANTH P，MEGHANA N，KANTHI K S.Rainbow connectivity：Hardness and tractability[C]//IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science，Mumbai，2011.

[4]LI X L，SUN X F.Upper bounds for the rainbow connection numbers of line graphs[J].Graphs Combin，2012，28（2）：251-265.

[5]DENG X C，XIANG K N，WU B.Polynomial algorithm for sharp upper bound of rainbow connection number of maximal outerplanar graphs[J]. Appl Math Lett，2012，25（3）：237-244.

[6]KLEINBERG J，TARDOS é.Algorithm Design[M].New Jersey：Addison Wesley，2005.

[7]BODLAENDER H.A linear time algorithm for finding tree decompositions of small treewidth[J].SIAM J Comput，1996，25：1305-1317.

（責任編校 馬新光）

FPT algorithm for sharp upper bound of rainbow connection numbers of a kind of graphs

DENG Xingchao
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

Based on the model of divide-and-conquer，an FPT algorithm for sharp upper bound of rainbow connection numbers of graphs with bounded treewidth is designed，and the algorithm is solvable in polynomial time.

rainbow connection number；model of divide-and-conquer；FPT algorithm；treewidth

O157.1

A

1671-1114（2016）05-0009-04

2015-09-28

天津師范大學博士基金資助項目(52XB1206).

鄧興超（1980—），男，講師，主要從事圖論和組合數學方面的研究.