局部連續Domain的特征與濃度

張則則，姜廣浩

（淮北師范大學數學科學學院，安徽 淮北 235000）

局部連續Domain的特征與濃度

張則則，姜廣浩

（淮北師范大學數學科學學院，安徽 淮北 235000）

引入局部連續Domain的局部基和稠密子集的概念，在此基礎上定義了局部連續Domain的特征與濃度.給出了局部基的刻畫，并討論局部連續Domain的特征、濃度與局部連續Domain帶上Scott拓撲或局部Lawson拓撲時的拓撲空間的特征、濃度之間的關系.

局部連續Domain；局部基；稠密子集；特征；濃度；Scott拓撲；局部Lawson拓撲

1 引言與預備知識

連續Domain結構作為計算機程序設計語言的指稱語義學的數學模型，受到很多理論計算機專家和格上拓撲學方面的學者的關注[1-2].作為這種趨勢的一個標志，Abramsky等[3]以連續Domain為主要對象系統闡述了經典Domain的數學理論.文獻[4]提出了連續Domain的特征與濃度.文獻[5]提出了局部連續Domain的定義.文獻[6]給出了局部連續Domain的權的定義及性質.本研究在局部連續Domain中給出局部基的刻畫，引入局部連續Domain的特征與濃度的概念，并討論局部連續Domain的特征、濃度與局部連續Domain帶上Scott拓撲或局部Lawson拓撲時的拓撲空間的特征、濃度之間的關系.

定義1[1-2]設（D，≤）為偏序集，S?D，若S≠○，并且S中的任意2個元在S中都有上界，即?a、b∈S，有c∈S，使得a≤c，b≤c，則稱S是定向的或為D的定向子集.

定義2[5]設（D，≤）為偏序集，?d∈D，規定↓d= {x∈D：x≤d}.若對每個d∈D，↓d為dcpo，則稱D是局部定向完備集，簡稱D是局部dcpo.記為定向集A?↓d在↓d中的上確界.

定義3[5]設D為局部dcpo，x、y∈D.若對D中任意一個有上界的定向集B與它的任一上界d，當時，存在b∈B，使得x≤b，則稱x雙小于y，簡記為x?y.記d={x∈D：x?d}，?d={x∈D：d?x}.

定義4[6]設D為偏序集，若對任意x∈D，?x是定向的，則稱D是局部定向集.

注1 定向集一定是局部定向集,反之不一定成

立.如圖1中的偏序集P={a，b，c，d，e，m}.

定義5[5]設D為局部dcpo，若對每個d∈D，?d為定向集并且，則稱D是連續的局部dcpo，簡稱局部連續Domain.

命題1[5]設P是局部dcpo，?x、y、u、v∈P，下列結論成立

（1）若x?y，則x≤y.

（2）若x≤y?u≤v，則x?v.

（3）若x?z，且P為局部連續Domain，則存在y∈P，使得x?y?z.

（4）若x?z，y?z，且x∨y在P中存在，則x∨y?z.

（5）若P中含有最小元素0，則0?x.

定義6[5]設P為局部dcpo，U?P是Scott開的當且僅當以下條件成立

（1）U={x∈P：?u∈U，u≤x}，即U是上集；

P中所有Scott開集構成的集族稱為P的Scott拓撲，記為σl（P）.Scott拓撲空間（P，σl（P））簡記為Σl（P）.

注2圖1中的U={a，d，e，m}為P的Scott開集.

定義7[6]設P為局部dcpo，B?P，稱B是P的一個基，若?x∈P，存在局部定向子集Bx，使得Bx?B∩x且∨Bx=x.

定理1[6]設P是局部連續Domain，則以下結論成立

（1）{?x：x∈P}是（P，σl（P））的基.

（2）x?y當且僅當↑x是y的局部鄰域.

（3）U?P是Scott開的，當且僅當↑U=U?P，y∈U時，存在x∈U，使得x?y.

定義8 設P是局部dcpo，定義λl（P）=σl（P）∨ω（P），其中ω（P）是以{P↑x：x∈P}為子基的上區間拓撲，則λl（P）是以σl（P）∨ω（P）為子基生成的拓撲.稱λl（P）為P上的局部Lawson拓撲.拓撲空間（P，λl（P））簡記為Λl（P）.

由局部Lawson拓撲的定義知，{U↑F：U∈σl（P），F是P的有限子集}是Λl（P）的一個基.

命題2 若P是局部連續Domain，B是P的基，則﹛?x↑F：x∈B，F是P的有限子集﹜是Λl（P）的一個基.

證明 由于?x∈σl（P），由局部Lawson拓撲的定義知﹛U↑F：U∈σl（P），F是P的有限子集﹜是Λl（P）的一個基，從而﹛?x↑F：x∈B，F是P的有限子集﹜是Λl（P）的一個基.

定理2 設P是局部dcpo，若P滿足下列條件

（1）P有插值性質:若a、b∈P，a?b，則存在c∈P，使得a?c?b；

（2）集族{?a：a∈P}構成Σl（P）的基；

（3）?a∈P，↑a=∩{U：U∈Σl（P），a∈U}.

則P是局部連續Domain.

當a∈U，U∈Σl（P）時，由（2）有b∈P，使得a∈?b?U.從而x∈?b?U.因此x∈∩{U：U∈Σl（P），a∈U}=↑a，即a≤x.故P是局部連續Domain.

2 局部連續Domain的特征

定義9 設P為局部dcpo，?x∈P，若Dx??x且∨Dx=x（其中Dx是局部定向集），則稱Dx是x的局部基.

定義10 設P為局部連續Domain，?x∈P，令χl（x，P）=min{|Dx|：Dx是x的局部基}，則稱χl（x，P）為局部連續Domain P中x點的特征.令χl（P）=sup{χl（x，P）：x∈P}，稱χl（P）為局部連續Domain P的特征.

記χl（x，Σl（P））為拓撲空間Σl（P）中點x的特征，χl（Σl（P））為拓撲空間Σl（P）的特征.

定義11 設P為局部連續Domain，若χl（x，P）≤ω（正整數集的基數），則稱P為第一可數的局部連續

Domain.

命題3 設P是局部連續Domain，?a∈P，有下列結論成立

（2）若a?a，且Da是a的局部基，則a∈↓Da.

（3）若b≤a，且Da、Db分別是a、b的局部基，則Db?↓Da.

證明 （1）由定義9易得.

（2）因為Da是a的局部基，所以∨Da=a且Da??a（其中Da是局部定向集）.由a?a的定義知，對于定向集↓Da，當a≤∨Da=↓Da時，有a∈↓Da.

（3）因為Da、Db分別是a、b的局部基，所以Da?a，Db?b，且∨Da=a，∨Db=b（其中Da、Db為局部定向集）.?y∈Db，有y?b.又因為b≤a，故y?a.而a=∨Da=∨↓Da，由y?a的定義知y∈↓Da.因此Db?↓Da.

定理3 設P是局部連續Domain，?a∈P且D??a，則D是a的局部基當且僅當?c∈?a，存在d∈↓D，使得c?d.

證明 充分性 首先證明D是局部定向集，即?d∈D，?d是定向集.?d1、d2∈d，則d∈?d1∩?d2.由于P是局部連續Domain，故{?x：x∈P}是（P，σl（P））的基，從而存在d3∈P，使得d∈?d3??d1∩?d2.于是d3?d.由命題1知，?c∈P使得d3?c?d.從而c∈?d3??d1∩?d2.因此c∈d且d1≤c，d2≤c，即d是定向的.顯然a=∨a≤∨D≤a，從而a=∨D.因此D是a的局部基.

證明 充分性 要證明D是a的局部基，只需證明a=∨D.顯然∨D≤a.下證a≤∨D.假設則存在d∈D，使得則由條件知，存在d∈D，使得，矛盾.因此a=∨D.故D是a的局部基.

證明 充分性 由定理3充分性的證明知D是局部定向集.易得a≤∨D=∨↓D≤a.因此∨D=a.從而D是a的局部基.

必要性 由定理3易得.

定理6 設P是局部dcpo，則P是局部連續Domain當且僅當?x∈P，x有局部基.

證明 由定義1及定義9易得.

定理7 設P是局部連續Domain，wl（P）=min{|B|：B是P的基}，則χl（P）≤wl（P）.

證明 設B是局部連續Domain P的基，且|B|= wl（P）.?x∈P，令Bx=B∩x，則x=∨Bx.故Bx是x的局部基.從而χl（x，P）≤|Bx|≤|B|=wl（P）.由x的任意性知χl（P）≤wl（P）.

定理8 設P是局部連續Domain，則

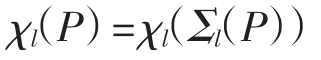
證明 先證明χl（Σl（P））≤χl（P）.?x∈P，存在x的局部基Dx，使得|Dx|≤χl（P）.

令β={?y：y∈Dx}.顯然β?σl（P）.?U∈σl（P），若x∈U，則∨Dx∈U，從而存在d∈U∩Dx，使得x∈?d?U.故β是x的鄰域基.因此χl（x，Σl（P））≤|Dx|≤χl（P）.

再證明χl（P）≤χl（Σl（P））.?x∈P，存在Σl（P）中x的一個鄰域基β，使得|β|≤χl（Σl（P））.?U∈β，由于x∈U，且U是Scott開集，故存在y∈U，使得x∈?y?↑y?U.取這樣的y記作yU.設D={yU：U∈β}.下證D是x的一個局部基.顯然D??x.?z∈P，若z?x，即x∈?z，由β是x的鄰域基知，存在U∈β，使得x∈U??z.又因為U是Scott開集，則存在y∈U，使得x∈?y?↑y?U??z.從而存在yU∈U，使得z?yU.由定理3知D是局部連續Domain P中x點的一個局部基.故χl（x，P）≤|D|≤χl（Σl（P））.由x的任意性知，χl（P）≤χl（Σl（P））.從而在局部連續Domain P中，有χl（P）≤χl（Σl（P））.

推論1 設P為局部連續Domain，則P是第一可數的局部連續Domain當且僅當Σl（P）是第一可數的拓撲空間.

證明 由定義11及定理8易得.

3 局部連續Domain的濃度

定義12 設P為局部連續Domain，A?P.若?x∈P及?y∈?x，存在a∈A，使得y?a，則稱A為P的稠密子集.

定理9 設P是局部連續Domain，A?P，則A為

P的稠密子集當且僅當?x、y∈P，當x?y時，存在a∈A，使得x?a.

證明 由定義12易得.

定義13 設P為局部連續Domain，令dl（P）= min{|A|：A是P的稠密子集}，稱dl（P）為局部連續Domain的濃度.特別地，若dl（P）≤ω，則稱局部連續Domain P是可分的.

記dl（Σl（P））、dl（Λl（P））分別為拓撲空間（P，σl（P））、（P，λl（P））的濃度.

定理10 設P是局部連續Domain，則

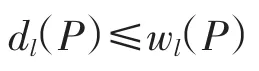
證明 設B是P的基，?x∈P，y∈?x，則存在b∈B，使得x?b?y.由定理9知，B是P的稠密子集.故dl（P）≤wl（P）.

定理11 設P是局部連續Domain，則dl（Σl（P））= dl（P）≤dl（Λl（P））.

證明 設A為P的稠密子集，且d（lP）=|A|.?U∈σ（lP），且U≠○.由定理1知，存在x、y∈U，使得x?y.由定理9知，存在a∈A，使得x?a.又U是上集，則a∈U，即A∩U≠○，所以A在Σ（lP）中稠密，且d（lΣ（lP））≤d（lP）.

設A在Σ（lP）中稠密，且d（lΣ（lP））=|A|.?x∈P，y∈?x，因為?x是Scott開集，所以A∩?x≠○，即存在a∈A，使得x?a.由定理9知，A為P的稠密子集.從而d（lP）≤|A|≤d（lΣ（lP））.

因為σl（P）?λl（P），所以dl（Σl（P））≤dl（Λl（P））.因此dl（Σl（P））=dl（P）≤dl（Λl（P））.

推論2 設P是局部連續Domain，則

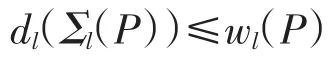
推論3 設P是局部連續Domain，則P是可分的當且僅當Σl（P）是可分的.

定理12 設P是含有最小元的局部連續Domain，則dl（Λl（P））≤wl（P）.

證明 令0為P中的最小元，B是P的一個基，且|B|=wl（P），則必有0∈B.顯然B是P的稠密子集，且也是Σ（lP）的稠密子集.

下面只需證明B在Λ（lP）中稠密.因為P↑F≠○（其中F是P的有限子集且是下集），所以0∈P↑F，從而B∩（P↑F）≠○.故B在Λ（lP）中稠密.因此d（lΛ（lP））≤w（lP）.

推論4 設P是含最小元的局部連續Domain，則dl（Λl（P））≤dl（P）+1.

證明 由定理11的證明過程可知，A在P中稠密當且僅當A在Σl（P）中稠密.故若A在P中稠密且dl（P）=|A|，則A在Σl（P）中稠密，從而A∪{0}也在Σl（P）中稠密.又0∈A∪{0}，且由定理12的證明可知，A∪{0}在下拓撲中稠密，從而A∪{0}也在Λl（P）中稠密.故dl（Λl（P））≤|A∪{0}|≤|A|+1≤dl（P）+1.

推論5 設P有最小元，則P是可分的局部連續Domain當且僅當Λl（P）是可分的空間.

[1]GIERZ G，HOFMAN K H，KEIMEI K，et al.Continuous Lattices and Domains[M].Cambridge:Cambridge University Press，2003.

[2]鄭崇友，樊磊，崔宏斌.Frame與連續格[M].北京：首都師范大學出版社，2000. ZHENG C Y，FAN L，CUI H B.Frame and Continuous Lattices[M]. Beijing：Capital Normal University Press，2000（in Chinese）.

[3]ABRAMSKY S，JUNG A.Domain Theory[M].Oxford:Oxford University Press，1994.

[4]趙彬，劉妮.連續Domain的特征與濃度[J].陜西師范大學學報：自然科學版，2002，30（2）：1-6. ZHAO B，LIU N.Character and density on continuous Domains[J]. Journal of Shaanxi Normal University:Natural Science Edition，2002，30（2）：1-6（in Chinese）.

[5]管雪沖，王戈平.一類局部定向完備集及其范疇的性質[J].數學進展，2005，34（6）：677-682. GUANG X C，WANG G P.A kind of local directed complete sets and properties of the categories[J].Advances in Mathematics，2005，34（6）：677-682（in Chinese）.

[6]ZHANG Z Z，JIANG G H.Locally continuous Domains and some applications[J].International Journal of Applied Mathematics and Statistics，2016，55（1）：41-50.

（責任編校 馬新光）

Character and density on locally continuous Domains

ZHANG Zeze，JIANG Guanghao
（School of Mathematical Science，Huaibei Normal University，Huaibei 235000，Anhui Province，China）

The concepts of the local base and dense set of locally continuous Domains are introduced and examined.On the basis of this，the character and density on locally continuous Domains are defined.In addition，some characterizations about the local base are given.The relations between the character and density on a locally continuous domain and those on the related topological space with Scott topology or locally Lawson topology are discussed.

locally continuous Domains；local base；dense set；character；density；Scott topology；locally Lawson topology

O153.1

A

1671-1114（2016）05-0013-04

2016-02-05

國家自然科學基金資助項目（11361028）；安徽高等學校省級自然科學研究重點資助項目（KJ2013A236，KJ2016A648）.

張則則（1989—），女，碩士研究生.

姜廣浩（1973—），男，副教授，主要從事一般拓撲學方面的研究.