一次兼顧“理論與實用”的微課制作

阮珣

1.問題的提出

現如今大家都提倡將信息技術與數學課程相結合，也意識到數學教育的形式可以多樣化，時間和地點也不再局限于課堂和教室中，微課以其“個性化”、“草根性”、“細、精、巧、透”的特點，在中小學數學教學中流行起來，多樣化微課比賽的開展、各種錄課程序的開發等等都體現了一線教師和相關工作者對微課的熱情。

在微課熱的背景下，我們如何做好微課，達到提高教學效果的目的呢？有專家提出要以教學應用為導向，以知識點為核心來組織微課的設計及制作也有學者提出，微課雖然是普通課程的一個縮影或者片段，但仍然要在一定的理論框架或模式下進行設計，如何設計和制作出一節理論背景扎實、教學實用性強的微課，就成了現在微課制作者們需要考慮的問題。

2.基于“轉化”思想的微課設計

2.1微課

微課的定義尚未得到統一，張一春教授認為，微課是為了使學生自主學習獲得最佳效果，經過精心的信息化教學設計，以流媒體形式展示的圍繞某個知識點或教學環節而開展的簡短、完整的教學活動因為微課強調學生的自主學習，所以微課的教學設計要充分體現“以生為本”的教學思想，

在微課教學內容的選擇上要充分考慮學生的認知水平，選擇教學中的重點、難點或疑點，排除一些不適合做成微課的內容，例如，在課本中已經講解得很詳細的內容、不需要制作微課學生就能學會的簡單內容。

微課“麻雀雖小，五臟俱全”，設計微課時要考慮到學習過程的連貫性，教學環節的完整性以及解決在流媒體形式下如何突破師生互動的難題，在實際操作中，時間的分配也是一個重要的考慮因素，

微課的展現形式有多種，可以教師出鏡教學，也可以通過播放課件，還可以將二者結合起來，因為微課本身具有局限性——不能體現與學生的直接互動，所以很容易被人們誤解成是對學生“填鴨式”的灌輸知識，其實對于不同類型的知識選擇不同的教學方法，這在主流的教學中已經有了成熟的模式，只是在微課的設計中，要注意給學生“留白”，學生也可以根據自己的實際情況選擇重復收看、暫停思考后再收看等方式來使用好微課。

總之，微課的設計不是突然出現的新生事物，可以對比平常的教學設計，結合微課對象的實際情況和需要來進行設計，微課的內容不能脫離課程標準，要把最重要的并且也適合用微課形式展現的內容提煉出來，結合相應的教學方法，設置連貫的教學環節，形成完整的一節課。

2.2“轉化”的數學思想

對于中小學數學學科的微課設計而言，微課制作者們常采用以“問題導學”的教學模式，數學學科的問題解決要求學生要具備數學學科知識和能力，因此在討論數學問題解決的時候，經常提到“轉化”的數學思想，波利亞在“怎樣解題表”中，通過不斷地把原問題轉化為已經解決的、等價的、類似的問題，經歷從特殊問題到一般問題，再到更一般問題……著名女數學家雅諾夫斯卡婭也曾說過：“解題就是把題歸結為已經解過的題，”因此“把未知的、待解決的問題轉化為己知的、已解決的問題，從而解決問題的過程”被稱為“化歸”，也被稱為“轉化”。

將“轉化”思想用于微課的教學設計中時，需要設置一系列呈階梯式難度遞增的問題，通過解決問題讓學生體驗由舊知推出新知，由特殊情況推出一般情況，這樣的學習過程既避免了學生對新知識的恐懼，又能通過實際操作去體會轉化的數學思想，還能經歷數學的“再發現”過程，可謂“一舉多得”。

2.3微課的教學設計

微課從本質上來說還是一個教學設計下的產物，因此微課的教學設計可以采用ADDIE教學設計模型，這個模型包括分析、設計、開發、實施和評價五個階段。

在教學設計的分析階段，既要分析教學內容、確定教學目標，也要分析微課的應用對象，評定學生的需求；制作者需要根據分析的結果設計合適的教學環節，選擇相應的教學方法以及采用適當的微課形式；在開發階段，制作者需要編寫教案、制作課件、準備必要的軟件和設備；在實施階段，需要制作者多次錄制微課，根據錄制情況對內容和方法進行及時地調整；最后，制作者對設計出來的微課進行自我評價以及請專業人士進行知識上和技術上的評價。

3.“轉化”的數學思想指導下的微課制作實例

3.1制作者的分析

制作者選擇的微課教學內容為人教版高中數學必修4第一章第二節的第一課時，即“任意角的三角函數的定義”，此定義是三角函數這一章中最基本的概念，是其他知識學習的出發點，在此前學生已經學習了用邊長之比來表示銳角三角函數，對三角函數有了初步的認識，并且也學習了“角的概念的推廣”的知識，因此，學生具備了學習這一內容的知識和能力。

這一節要學習的定義與初中的知識有質的區別，初中時對銳角三角形的三角函數進行定義并且將定義用于解三角形，而高中是對任意大小的角的三角函數進行定義，并且更加強調三角函數的函數性質，這是易錯點，也是重點知識，因此將教學目標設置如下：（1）借助單位圓理解任意角的三角函數的定義；（2）能根據任意角的三角函數的定義求出具體的角的各三角函數值；（3）在定義的學習過程中培養學生類比、分析及解決問題的能力；（4）在定義的學習過程中體驗數形結合的數學思想和體會數學的再發現的過程。

3.2制作者的設計

制作者選擇以“任意角的三角函數的定義”作為教學內容，提出驅動性問題：任意角的三角函數應該如何定義？

根據學生已有的知識和能力水平，制作者將驅動性問題轉化為一系列問題，這一系列問題可能涉及到銳角三角函數、坐標系、單位圓、任意角的知識，也要用到類比、轉化和數形結合的數學思想，

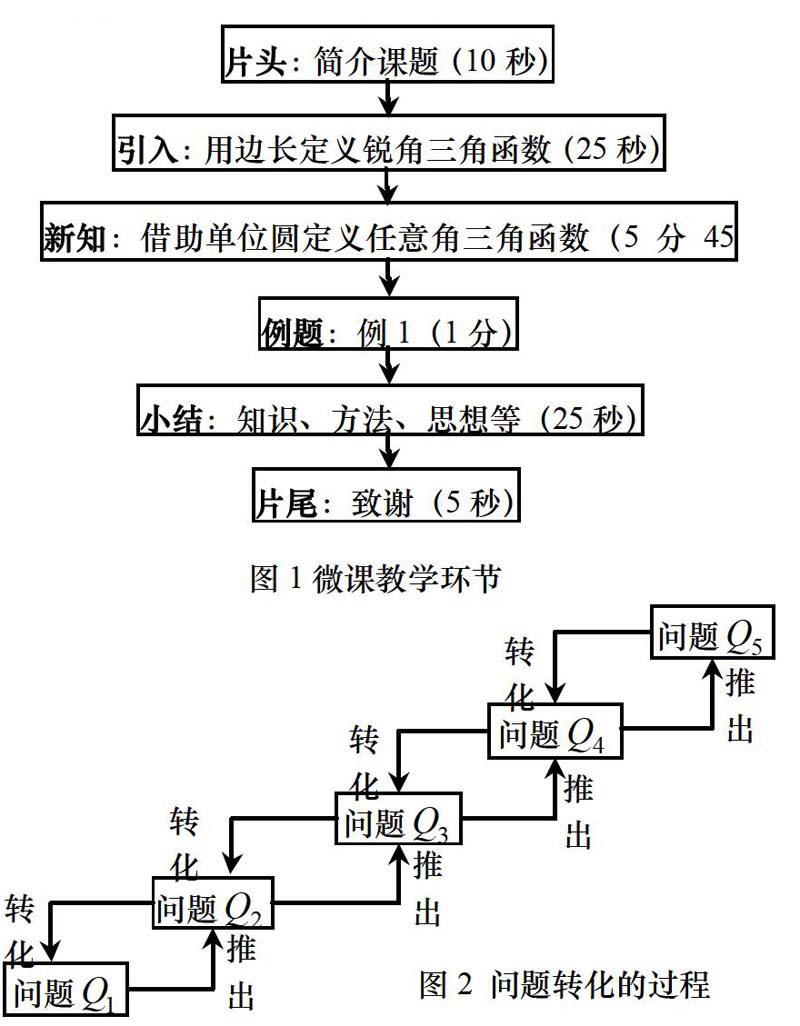
整個微課時長設置在8分鐘以內，包括片頭、復習引入、探究新知、例題講解、小結和片尾六個環節（圖1），在復習引入和探究新知兩個環節（圖2），制作者將驅動性問題“多步化歸”后，提出一個問題串，這個問題串以階梯式的形式出現，引導學生通過已經學過的知識去解決新的問題，直至最終解決了驅動性問題，以復習引入和探究新知兩個環節為例，復習引入環節的主要內容是提出問題Q₁，探究新知環節的主要內容是提出并解答問題Q，Q₃，Q₄，Q₅，具體設計如下：

Q₁：如何用對邊、鄰邊、斜邊表示銳角a的三角函數呢？

Q₂：如何用坐標表示銳角α的三角函數呢？

Q₃：如果把P點移動到角a終邊的其他位置時，銳角a的三角函數會不會發生改變呢？

Q₄：如何借助單位圓來定義銳角a的三角函數呢？

Q₅：當角a是任意角時，該如何定義它的三角函數呢？

3.2.1問題Q₁的設計

在復習導入環節，制作者直接提出問題Q₁：在初中數學學習中，我們是如何定義銳角α的三角函數的呢？學生可以通過回憶初中數學的知識，在直角三角形中用對邊、鄰邊、斜邊這三邊之比來表示銳角α的三角函數。

3.2.2問題Q₂的設計

對于任意角而言，是不能直接用邊長之比來表示任意角的三角函數的，在上一節中學習“角的概念的推廣時”，學生學過借助直角坐標系表示任意角，在此基礎上提出問題Q₂：在直角坐標系中，如何用坐標來表示銳角α的三角函數？

3.2.3問題Q₃的設計

在高中階段的學習中，三角函數不僅是解三角形的工具，更是具備函數性質的一種重要的函數，為了更深入地學習三角函數性質，提出問題Q₃：如果把P點移動到角α終邊的其他位置時，銳角的三角函數會不會發生改變呢？

通過相似三角形的知識，可以證明銳角α的三角函數不會隨著P點在角α的終邊上位置的改變而發生改變，這為提出問題Q₄奠定了基礎，

3.2.4問題Q₄的設計

既然銳角a的三角函數不會隨著P點在角α的終邊上位置的改變而發生改變，那么不妨將OP的距離設為單位長度，可以提出問題Q₄：如何借助單位圓來定義銳角α的三角函數呢？

五個問題的設計充分地將待解決的問題轉化為已經解決的問題，通過單位圓和坐標來定義任意角的三角函數也使得學生能夠直觀地建立自變量α與函數值x，y之間的關系，為后面學習三角函數的其他性質奠定了基礎。

3.3教學設計的開發與實施

教學內容和環節的確定，制作者選擇用"WPS演示”制作課件，用Camtasia studio 8錄制微課，經過多次錄制、調整與后期制作，最后生成了時長7分44秒的微課視頻。

在錄制過程中，通過語言引導學生回憶已經學習過的知識或者解決的問題，銜接每個環節，通過在屏幕左方展示圖形，圖形右方展示問題和公式，將數與形相互結合，讓學生對定義產生更加直觀的認識，通過在圖中用不同顏色的筆跡標注角和坐標，類比銳角和任意角的三角函數定義的聯系與區別，制作者在每個環節末尾都進行了知識點或者方法的提煉，突出微課“精”、“透”的特點。

為了提高微課的教學效果，降低學生使用微課的難度，制作者放慢了旁白的語速，做到頓挫有致，在需要學生暫停視頻、獨立思考的地方停頓了幾秒或者提醒學生點擊暫停，在后期制作中制作者也對音頻進行了降噪和混音處理，讓音頻更加悅耳。

3.4教學設計的評價與反思

盡管這節微課還沒有大面積投放給學生使用，但是通過訪談幾位一線教師、微課專家和學生，可以發現，他們都對這節微課給予了知識上、技術上的好評，也從不同角度提出了一些意見，例如，來自一線教學的老師F認為任意角的三角函數的本質是一種函數，他建議制作者從函數的角度出發，從定義域等方面加深對三角函數的認識和理解，微課專家s建議講解的錄制要有對象感，要當做有30個學生在聽課，一些學生普遍建議在課件中使用一些動圖，讓微課更充滿趣味性。

在制作微課時，要求制作者既要具備優秀數學教師的數學素養和教學能力，又要求制作者將信息技術與數學教學有機地結合起來，在微課類的設計活動中，需要制作者從使用者的角度來設計微課，又需要從專業的技術人員的角度挑剔每一個細節，還要保持對新鮮事物的求知欲和探索欲。

4.結束語

通過查閱文獻和多次實踐，這次微課制作既具備了扎實的理論基礎，又要考慮到教學內容的選擇和特點，還兼顧了微課的實用性，讓微課真正地服務于學生，在未來的研究中還可以形成系統的教學模型，力圖做成一個系列的簡短但不簡單的微課。