空氣耦合超聲斜入射均勻彈性層狀介質材料的傳播特性

王興國， 吳文林， 陳正林， 吳南星

(景德鎮陶瓷大學 機械電子工程學院, 江西 景德鎮 333403)

?

空氣耦合超聲斜入射均勻彈性層狀介質材料的傳播特性

王興國， 吳文林， 陳正林， 吳南星

(景德鎮陶瓷大學 機械電子工程學院, 江西 景德鎮 333403)

針對空氣耦合超聲非接觸、無損傷技術在均勻彈性層狀介質材料中應用缺少相關理論依據的問題，從波動方程入手，利用傳遞矩陣法及聲波氣體與固體邊界條件研究了空氣耦合超聲波以不同的入射角和檢測頻率在均勻彈性層狀介質中的聲傳播規律，建立了基于空氣耦合的均勻層狀彈性材料檢測方法。模擬結果表明：斜入射時，透射系數分布呈現多模式形態；當入射角超過橫波臨界入射角時，發生全反射現象；隨著檢測頻率的逐漸增大，入射臨界角逐漸變小；隨著聲入射角逐漸增大，截止聲波頻率與介質厚度積也逐漸增大。實驗驗證表明，實驗結果與數值模擬結果基本吻合。

材料檢測與分析技術； 空氣耦合; 波動方程; 透射系數; 均勻彈性； 層狀介質

0 引言

隨著材料科學技術的發展，各種先進高性能材料已廣泛應用于電站鍋爐、航天航空、石油管道等許多軍事和民用領域[1-2]，由于高溫、疲勞損傷以及材料老化等各種惡劣環境不利因素的影響，材料的力學性能將不可避免發生退化[3]。這些都會影響到材料的安全性和可靠性。因此研究關鍵零部件力學性能的檢測就顯得尤為重要。

目前，測量材料力學性能方法大致可以歸類為有損檢測法和無損檢測方法。隨著無損檢測技術和方法不斷改進，無損檢測作為一種非破壞的檢測技術越來越受到青睞。其中，超聲檢測在無損檢測方法中具有快速性、檢測方法簡單、方法多樣、應用范圍廣等優點，廣泛應用于材料內部缺陷和性能退化等方面的測量，例如，縱波脈沖回波法[4-5]、蘭姆波法[6-7]和表面波法[8]等。然而在傳統的超聲方法需要耦合劑來完成檢測過程，在高溫和不宜使用耦合劑等環境下，傳統的超聲測量手段顯得無能為力了。早在20世紀60年代就提出非接觸式空氣耦合超聲檢測技術，該技術以空氣作為檢測試樣和換能器間的聲傳播耦合劑，這種檢測技術具有真正的非接觸檢測，無換能器接觸表面的磨損及非破壞、非浸入及安全無害的特點，使得其在惡劣條件下檢測均勻彈性層狀材料性能中具有不可替代的優勢[9-10]，因此空氣耦合式超聲波無損檢測技術在其他工程檢測領域的應用也越來越廣泛[11-13]。

近年來，非接觸空氣耦合超聲檢測技術得到眾多學者和研究人員的關注[14-15]。然而，國內僅少數學者針對空氣耦合條件下的超聲傳播 特性進行了理論研究[14,16]，缺少相關的實驗驗證。本文通過研究空氣耦合超聲縱波在均勻彈性層狀材料中的傳播機理建立了檢測數學模型；然后以有機玻璃作為檢測介質，研究了空氣耦合超聲在有機玻璃中的傳播特性，最后利用實驗檢測結果驗證了數值分析結果的正確性。

1 層狀介質空氣耦合檢測原理

1.1 物理模型

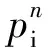
圖1 空氣耦合超聲檢測示意圖Fig.1 Physical model of air coupling ultrasonic test

1.2 數學方程及邊界條件

在每一層引入一個局部的坐標系統，其原點在該層的入射界面，根據聲壓波動方程和歐拉方程可以得到不同均勻彈性層狀介質中的聲壓pn和質點速度vn.

其中，第1層介質聲壓p1和質點速度v1表示方法為

(1)

第2層介質聲壓p2和質點速度v2表示為

(2)

由于在第3層介質中只有透射波，因此B3=0. 該層介質聲壓p1和質點速度v1表示為

(3)

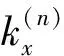
(4)

(5)

將邊界條件(4)式、(5)式代入(1)式、(2)式、(3)式，得到線性方程組并寫成(6)式矩陣AX=0形式為

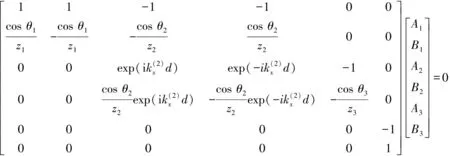
(6)

式中：矩陣為6×6矩陣，奇數行是每層介質質點聲壓，偶數行是每層介質質點振動速度。由于空氣作為超聲檢測換能器與被測材料之間的耦合介質，則z1=z3，通過求解方程組(6)式可得聲波在被測材料中的透射系數T為

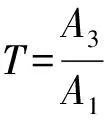
(7)

2 數值仿真分析

2.1 仿真材料

本文以單層均勻彈性層狀材料有機玻璃作為仿真材料，通過(7)式可以獲得空氣耦合超聲波以不同入射角有機玻璃的透射系數，表1給出了有機玻璃材料和空氣的聲學參數[14]。

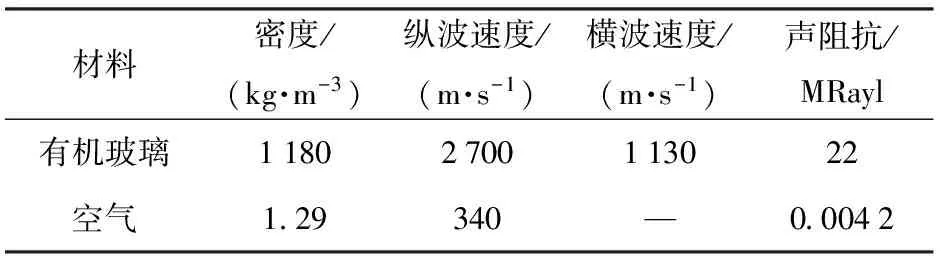
表1 有機玻璃和空氣的聲學參數表

2.2 斜入射聲傳播特性

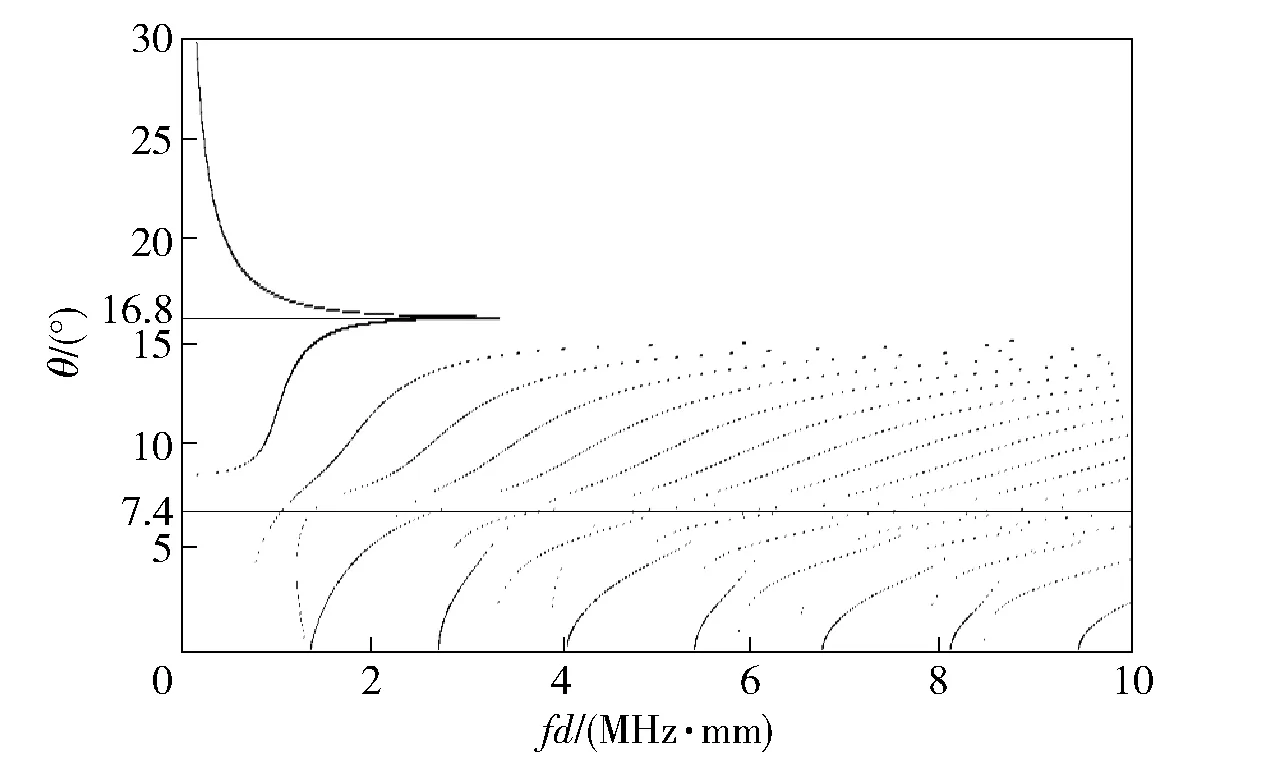
圖2 不同入射角和頻率與厚度積透射系數的分布Fig.2 Distribution of transmission coefficients under different the frequency-thickness products and incident angles

圖3給出了不同激勵頻率下入射角θ和透射系數T之間的關系。由圖3(a)可知，當激勵頻率為2.5 MHz時，最大入射臨界角為7°，透射系數幾乎為0；由圖3(b)可知，當激勵頻率為3.5 MHz時，入射臨界角為6.8°，透射系數幾乎為0；由圖3(c)可知，當激勵頻率為5 MHz時，入射臨界角為6.6°，透射系數幾乎為0. 由此可知，隨著檢測頻率的增大，入射臨界角會逐漸減小。當入射角超過入射臨界角時，發生全反射現象，此時透射系數為0.

圖4給出了在不同入射角下頻率與厚度積fd與透射系數T之間的關系。由圖4(a)可知，入射角θ=2°時，透射系數隨頻率與厚度積的增大逐漸減小，當頻率f>0.53 MHz，透射系數幾乎為0；由圖4(b)可知，入射角θ=5°時，透射系數隨頻率與厚度積的增大逐漸減小，當頻率f>0.61 MHz，透射系數幾乎為0；由圖4(c)可知，當入射角θ=7°時，透射系數隨頻率與厚度積的增大逐漸減小。當頻率f>0.748 MHz時，透射系數幾乎為0. 因此在空氣耦合超聲檢測時，入射角在最大臨界角度以內，隨著入射角不斷增大，用于檢測的頻率范圍越寬。當超過一定頻率后，透射系數幾乎為0. 因此采用空氣耦合超聲檢測均勻彈性層狀材料時，如何選擇合適的檢測頻率、入射角就顯得非常重要了。

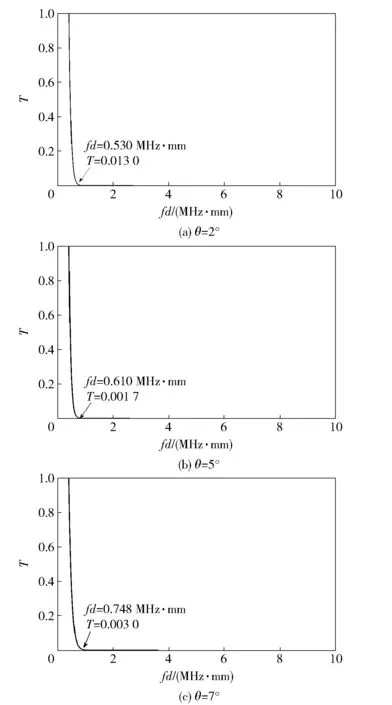
圖4 不同入射角下頻率與透射系數關系 Fig.4 Relation between frequency and transmission coefficient of acoustic wave at different incident angles

3 空氣耦合超聲檢測實驗方法

3.1 實驗材料

取厚度為5.5 mm有機玻璃一塊，經過加工后平面尺寸為150 mm×150 mm. 物理參數如下：密度為1 180 kg/m3，縱波速度為2 700 m/s，橫波速度為1 130 m/s. 具體參數見表1.

3.2 實驗系統

圖5給出了均勻彈性層狀材料穿透式空氣耦合超聲波檢測系統。其中，圖5(a)是超聲實驗檢測實物；圖5(b)檢測示意圖。該檢測系統由計算機、超高功率超聲發射/接收裝置、空氣耦合聚焦換能器、前置放大器、角度旋轉臺等構成。其中，空氣耦合超聲發射/接收裝置由日本Japan Probe公司生產，型號為JPR-10CN；聚焦換能的中心頻率分別為1 MHz、1.3 MHz、2.5 MHz、3.5 MHz、5 MHz，合計6對，每一對換能器一個用來發射信號，另一個用來接收信號。聚焦半徑均為40 mm，實驗中換能器發射電壓為600 V，采集頻率100 MHz，接收信號放大40.2 dB，通過角度旋轉臺實現均勻彈性層狀材料檢測過程中聲波以不同角度的入射和接收。

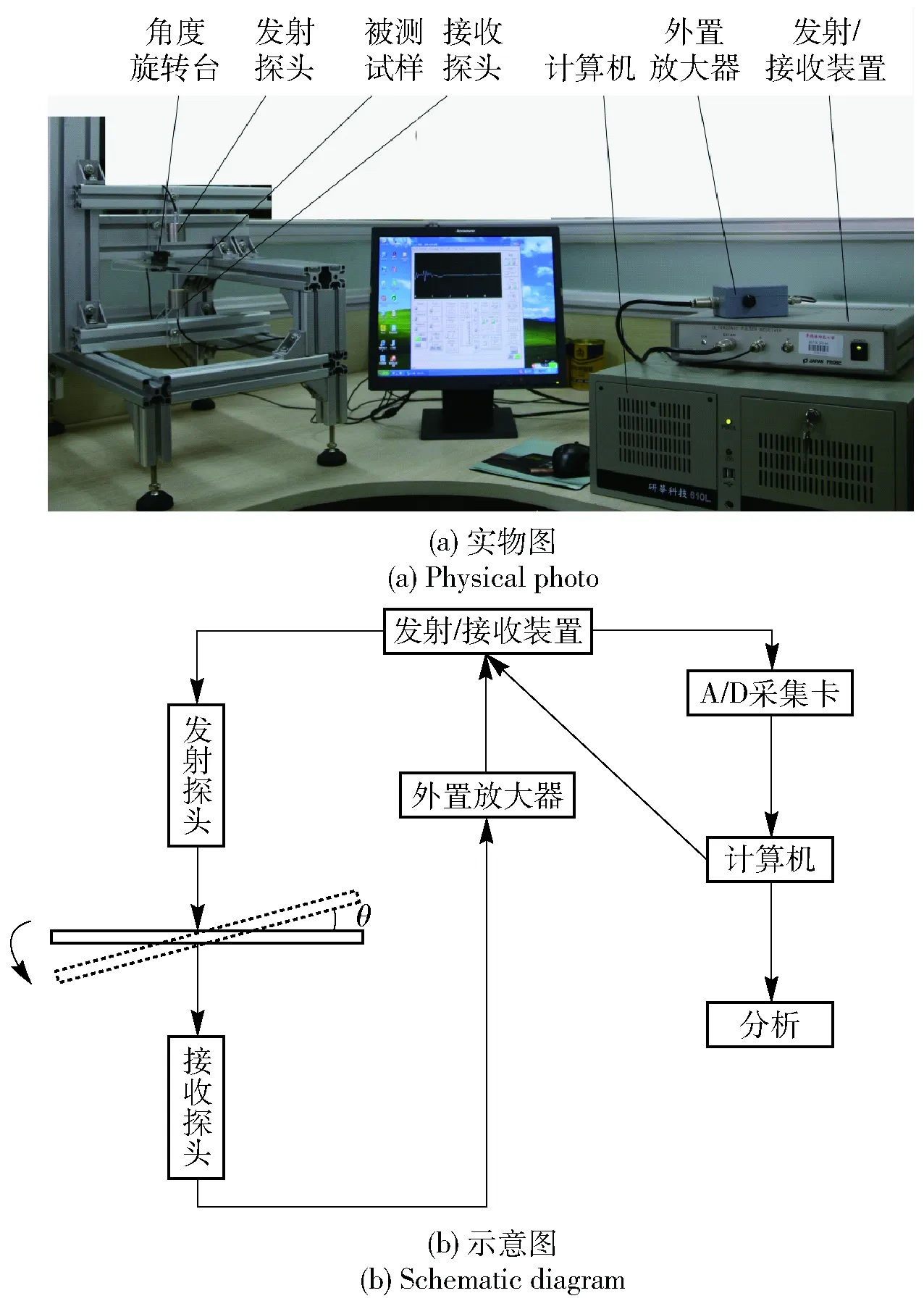
圖5 空氣耦合超聲波檢測系統Fig.5 Air-coupled ultrasonic testing system

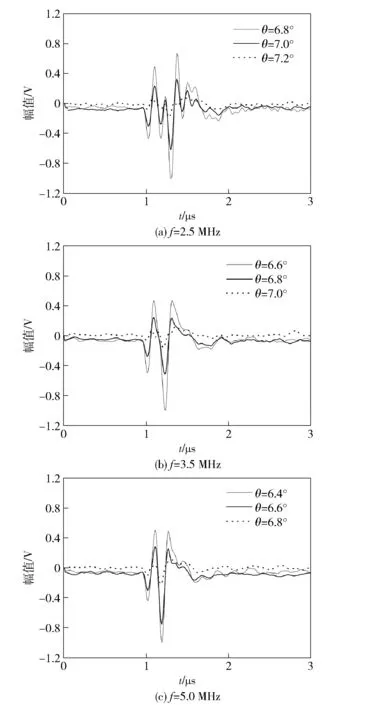
圖6 不同入射角下的透射波形Fig.6 Acoustic time-domains of air-coupling ultrasonic testing at different incident angles

3.3 檢測結果分析

圖6給出了不同入射角下的透射波形，圖6(a)是檢測頻率為2.5 MHz時不同入射角下的透射波形，其中細實線、粗實線、虛線分別為入射角6.8°、7°、7.2°的波形。由圖6可知，隨著入射角度的增大，時域波形幅值有逐漸減小的趨勢。當入射角7.2°時，波形幅值非常小，幾乎為0，入射角7°時波形的幅值略大于入射角7.2°. 該結果與圖3數值模擬結果剛好吻合。因此檢測頻率為2.5 MHz時入射臨界角為7°. 圖6(b)是檢測頻率為3.5 MHz時不同入射角的透射時域波形，細實線、粗實線、虛線分別是入射角為6.6°、6.8°、7°的時域波形。圖6(c)是檢測頻率為5 MHz時不同入射角的透射時域波形，其中細實線、粗實線、虛線分別是入射角為6.4°、6.6°、6.8°的時域波形。由圖6(b)、圖6(c)可知，該結果與圖6(a)的分析結果相似，這里不再贅述，其中當檢測頻率為3.5 MHz時的臨界角為6.8°；當檢測頻率為5 MHz時入射臨界角為6.6°. 從圖6中還可以看出，隨著檢測頻率的逐漸增大，入射臨界角逐漸變小。該結論與圖3數值分析結果基本吻合。

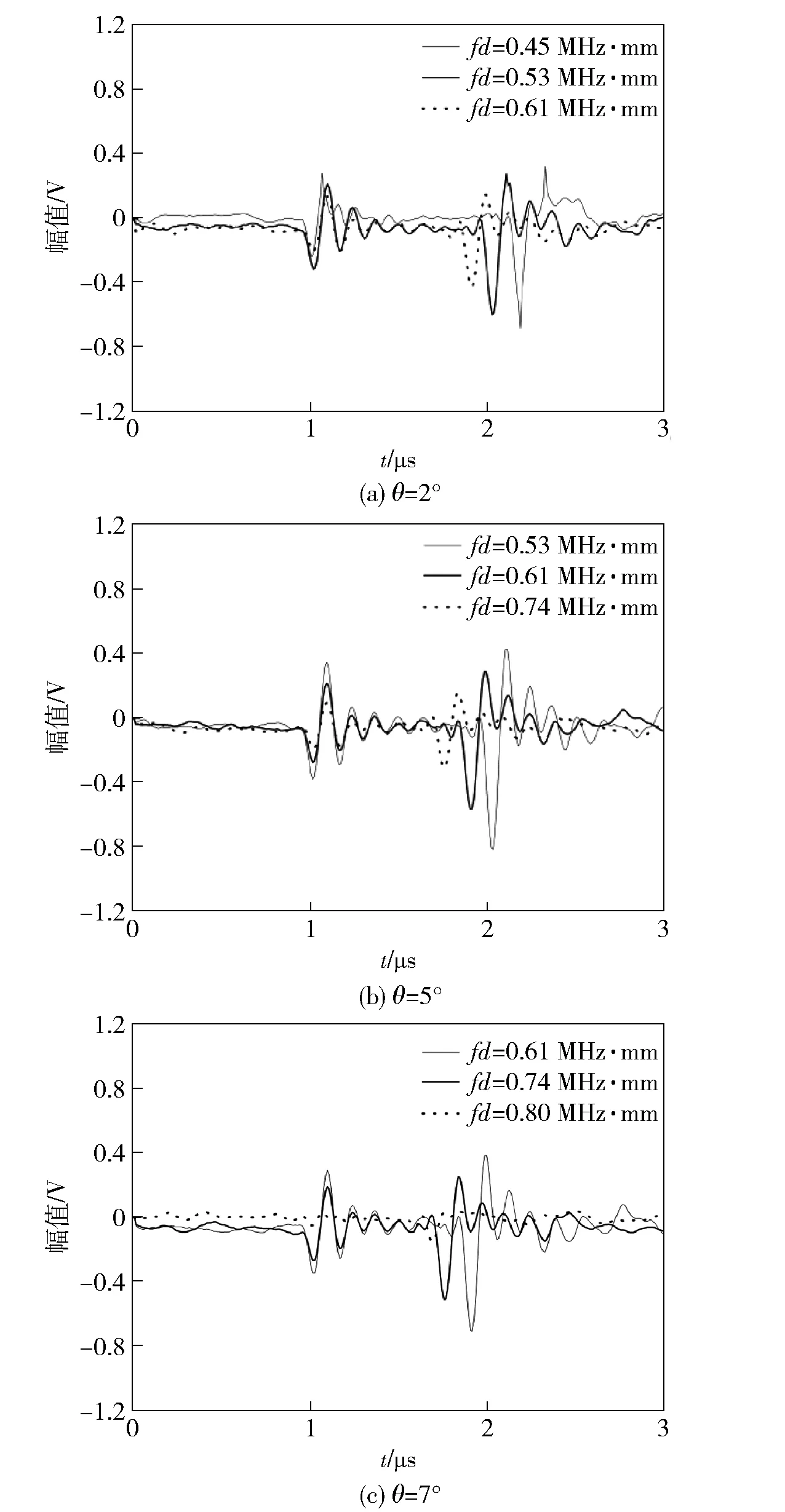
圖7 不同檢測頻率下的透射波形 Fig.7 Acoustic time-domain of air-coupling ultrasonic testing at different frequencies

圖7給出了不同檢測頻率下的透射波形。其中，圖7(a)為入射角2°時不同檢測頻率下的透射波形，其中細實線、粗實線、虛線分別代表頻率與厚度積為0.45 MHz·mm、 0.53 MHz·mm、0.61 MHz·mm的時域波形。由圖7(a)可知，與頻率與厚度積為0.45 MHz·mm的時域波形幅值相比，頻率與厚度積為0.53 MHz·mm的幅值較小，頻率與厚度積為0.61 MHz·mm的幅值最小。因此，當入射角為2°時的截止頻率與厚度積為0.53 MHz·mm；圖7(b)是入射角為5°時不同檢測頻率下的透射時域波形，細實線、粗實線、虛線分別是頻率與厚度積為0.53 MHz·mm、0.61 MHz·mm、0.74 MHz·mm的時域波形。圖7(c)是入射角為7°時不同檢測頻率下的透射時域波形，細實線、粗實線、虛線分別是率與厚度厚積為0.61 MHz·mm、0.74 MHz·mm、0.8 MHz·mm的時域波形。圖7(b)、圖7(c)的結果與圖7(a)相似，結論為當入射角為5°時的截止頻率與厚度積為0.61 MHz·mm；當入射角為7°時的截止頻率與厚度積為0.74 MHz·mm. 從圖7中還可以看出，空氣耦合超聲檢測的入射角逐漸增大時，截止頻率與厚度積也逐漸增大。這里需要說明的是，當頻率與厚度積0.61 MHz·mm和0.74 MHz·mm時，透射波幅值較小，略大于0，這與仿真結果幾乎為0的結果存在著一定的誤差。究其原因，這可能是由于在實驗檢測過程中換能器實際的中心頻率與標定的中心頻率并不完全一致，或者聲波在傳播過程中散射等不確定因素導致實驗結果具有一定的誤差。但該實驗結果也基本能夠驗證仿真結果(見圖4)的變化趨勢。

4 結論

利用傳遞矩陣法及聲波氣體與固體邊界條件得到了空氣耦合超聲波在有限厚度均勻彈性層狀材料中的聲控制方程，建立了基于穿透式空氣耦合超聲波檢測模式的實驗檢測系統。當空氣耦合超聲波斜入射有限厚度均勻彈性層狀材料時，聲波在氣體與固體邊界面上發生了波形轉換，透射系數分布呈現多模式形態，不同的模態均存在著截止頻率。從透射系數分布可知，隨著檢測頻率的不斷增大，相應的入射臨界角逐漸減小，該臨界角也就是橫波全反射臨界角；當入射角在入射臨界角以內時，隨著入射角不斷增大，用于檢測的頻率范圍也越大，入射角超過入射臨界角時將發生全反射現象。因此可以通過空氣耦合超聲斜入射檢測均勻彈性層狀材料橫波聲速及不同檢測頻率的最大入射角。

References)

[1] 馬潤波, 杜建華, 許世蒙. 銅基復合材料分類判別方法研究[J]. 兵工學報, 2015, 36(5):921-927. MA Run-bo, DU Jian-hua, XU Shi-meng. Research onclassification discriminating method of copper matrix composites[J]. Acta Armamentarii, 2015, 36(5): 921-927. (in Chinese)

[2] 吳南星, 陳正林, 廖達海. 基于lamb波在氮化硅陶瓷葉片及其作摩擦材料鍍層傳播特性的研究[J]. 陶瓷學報, 2015, 36(1): 83-87. WU Nan-xing, CHEN Zheng-lin, LIAO Da-hai. Based on the lamb wave research for propagation characteristics in the silicon nitride ceramic blade and its friction material coating[J]. Journal of Ceramics, 2015, 36(1): 83-87. (in Chinese)

[3] 程應科, 張建軍, 徐連勇. 涂層彈性模量的測量方法[J]. 中國科技論文在線, 2008, 3(4):293-298. CHENG Ying-ke, ZHANG Jian-jun, XU Lian-yong. Investigation on measuring the elastic modulus of coatings[J]. Sciencepaper Online, 2008, 3(4):293-298. (in Chinese)

[4] Byoung G K, Sekyung L, Kishi T. Time-domain reflection field analysis for ultrasonic evaluation of thin layered media[J]. NDT & E International, 1996, 29(5):317-322.

[5] 王興國, 常俊杰, 單英春, 等. 超聲回波信號檢測橡膠薄層的特性[J]. 機械工程學報, 2008, 44(10): 114-117. WANG Xing-guo, CHANG Jun-jie, SHAN Ying-chun, et al. Testing of characteristic of rubber thin layer by ultrasonic echo signal[J]. Journal of Mechanical Engineering, 2008, 44(10):114-117. (in Chinese)

[6] 張銳, 萬明習, 鞏欣洲，等. 低頻多模式超聲蘭姆波超薄彈性層定征方法[J]. 計量學報, 2000, 21(1):59-67. ZHANG Rui, WAN Ming-xi, GONG Xin-zhou, et al. Low frequency multi-mode ultrasonic lamb wave method for characterization of the ultra-thin elastic layer[J]. Acta Metrologica Sinica, 2000, 21(1):59-67. (in Chinese)

[7] 張銳, 萬明習. 超薄雙層復合結構界面特性超聲蘭姆波評價方法[J]. 航空學報, 2000, 21(4):313-316. ZHANG Rui, WAN Ming-xi. Ultrasonic guided wave method for evaluating the interface bonding property of ultra-thin two-layer composites[J]. Acta Aeronautica et Astronautica Sinica, 2000, 21(4):313-316. (in Chinese)

[8] Brekhovskikh L M. Waves inlayered media[M]. 2nd ed. New York: Academic Press, 1980.

[9] 周正干，魏東. 空氣耦合式超聲波無損檢測技術的發展[J]. 機械工程學報, 2008, 44(6):10-14. ZHOU Zheng-gan, WEI Dong. Progress of air-coupled ultrasonic non-destructive testing technology[J]. Chinese Journal of Mechanical Engineering, 2008, 44(6):10-14. (in Chinese)

[10] 董正宏, 王元欽, 李靜. 航天復合材料空氣耦合式超聲檢測技術研究及應用[J]. 裝備指揮技術學院學報, 2007, 18(2):79-84. DONG Zheng-hong, WANG Yuan-qin, LI Jing. Application and research on air-coupled ultrasonic testing for aerospace composite materials[J]. Journal of the Academy of Equipment Command & Technology, 2007, 18(2):79-84. (in Chinese)

[11] 左楊. Fe-Al2O3金屬陶瓷選擇性還原制備工藝研究[J]. 陶瓷學報, 2012, 33(2):176-180. ZUO Yang. Preparation of Fe-Al2O3cermet by partial selective reduction[J]. Journal of Ceramics, 2012, 33(2):176-180. (in Chinese)

[12] 孫國梁, 王剛, 張文杰. 金屬基陶瓷涂層的制備及涂覆工藝的研究[J]. 陶瓷學報, 2013, 34(3): 318-321. SUN Guo-liang, WANG Gang, ZHANG Wen-jie. Preparation of metal ceramic coatings and coating process[J]. Journal of Ceramics, 2013, 34(3):318-321. (in Chinese)

[13] 杜功煥, 朱哲民, 龔秀芬. 聲學基礎[M]. 南京: 南京大學出版社, 2013. DU Gong-huan, ZHU Zhe-min, GONG Xiu-fen. Fundamentals of acoustics[M]. Nanjing: Nanjing University Press, 2013. (in Chinese)

[14] 夏利利, 楊文革, 董正宏. 非接觸超聲檢測技術在航天無損檢測中的研究與應用[J]. 裝備指揮技術學院學報, 2007, 18(4):58-62. XIA Li-li, YANG Wen-ge, DONG Zheng-hong. Applications and research on air-coupled ultrasonic technique for aerospace nondestructive testing[J]. Journal of the Academy of Equipment Command and Technology, 2007, 18(4):58-62. (in Chinese)

[15] 常俊杰, 盧超. 非接觸空氣耦合超聲檢測原理及應用研究[J]. 無損探傷, 2013, 37(4):6-11. CHANG Jun-jie, LU Chao. Test principle and application research of noncontact air coupling[J]. Nondestructive Test, 2013, 37(4):6-11. (in Chinese)

[16] 劉磊, 楊揚, 潘永東, 等. 空氣耦合層狀復合材料的聲傳播研究[J]. 固體力學學報, 2014, 35(1): 8-14. LIU Lei, YANG Yang, PAN Yong-dong, et al. The study of wave propagation in the air-coupled composite laminate[J]. Chinese Journal of Solid Mechanics, 2014, 35(1):8-14. (in Chinese)

[17] 張海瀾. 理論聲學 [M]. 北京: 高等教育出版社，2012:203-205. ZHANG Hai-lan. Theoretical acoustics[M]. Beijing: Higher Education Press, 2012:203-205. (in Chinese)

Propagation Characteristics of Oblique Incidence Air Coupling Ultrasonic Wave in Uniform Elastic Layered Medium

WANG Xing-guo, WU Wen-lin, CHEN Zheng-lin, WU Nan-xing

(School of Mechanical and Electronic Engineering, Jingdezhen Ceramic Institute, Jingdezhen 333403, Jiangxi, China)

The propagation rules of air coupling acoustic wave in uniform elastic layered medium are studied at the different incident angles and testing frequency according to the wave equation. The transfer matrix method and the gas-solid boundary conditions of acoustic wave are used to solve the problem which lacks theoretical support in the application of non-contact ultrasonic test technology in uniform elastic material. A testing method of uniform elastic medium is developed. The stimulated results show that the transmission coefficient distribution presents a form of multimode. The total reflection occurs when the incident angle exceed the critical angle of transverse wave. The incident critical angle decreases with the increase in testing frequency. The cutoff frequency-thickness product increases with the increase in incident angle. The experimental results are in agreement with the numerical results.

materials examination and analysis; air coupling; wave equation; transmission coefficient; uniform elasticity； layered meduim

2016-02-02

國家自然科學基金項目(51305184、51565020)；南昌航空大學無損檢測技術教育部重點實驗室開放基金項目(ZD201429008)

王興國(1980—)，男，副教授。E-mail: xgwang@yeah.net

TB553

A

1000-1093(2016)11-2094-07

10.3969/j.issn.1000-1093.2016.11.018