On Pseudo Weakly J-clean Rings

胡小美, 陳煥艮

(杭州師范大學理學院, 浙江 杭州 310036)

?

On Pseudo Weakly J-clean Rings

A ringRis called a pseudo weakly J-clean ring if every elementa∈Rcan be written in the form ofa=e+w+(1-e)Raora=-e+w+(1-e)Rawhereeis an idempotent andwbelongs to the Jacobson radical. This paper explores various properties of pseudo weakly J-clean rings. A ringRis pseudo weakly J-clean if and only ifR[[x]], Hurwitz series ringH(R), trivial extensionT(R,M) andS(R,σ) are pseudo weakly J-clean, respectively. Furthermore, it proves that the following are equivalent, for anyn∈N,Sn(R) is pseudo J-clean, for anyn∈N,R[x]/(xn) is pseudo weakly J-clean, where (xn) is the ideal generated byxn. In particular, it characterizeS=R[D,C] is pseudo weakly J-clean under certain conditions. Also it shows that 2 is a unit inR, thenRis pseudo J-clean if and only ifRC2is pseudo J-clean.

pseudo weakly J-clean ring; Hurwitz series ring;S=R[D,C] ring; group ring; Jacobson radical; idempotent

1 Introduction

Following Qua[1], we call a ringRis pseudo weakly clean if every elementa∈Rcan be written in the form ofa=e+u+(1-e)Raora=-e+u+(1-e)Rawhereeis an idempotent anduis a unit. On the other hand, J-clean rings are studied by Chen[2]. A ringRis called a J-clean ring if every elementa∈Rcan be written in the form ofa=e+jwhereeis an idempotent andjbelongs to Jacobson radical. If we add an extra condition thatej=jeon the above definition it is called a strongly J-clean ring. Now, we combine pseudo weakly rings and weakly J-clean rings together and consider a new type of rings. We call a ringRis pseudo J-clean if every elementa∈Rcan be written in the form ofa=e+w+(1-e)Rawhereeis an idempotent andwbelongs to Jacobson radical and an elementa∈Ris said to be pseudo weakly J-clean if existe∈Id(R) andw∈J(R) such thata=e+w+(1-e)Raora=-e+w+(1-e)Ra.

We explore various properties of pseudo weakly J-clean rings, we proves that the direct product ringR=∏k∈IRkis pseudo weakly J-clean if and only if eachRkis pseudo weakly clean and at most oneRkis not a pseudo J-clean ring. A ringRis pseudo weakly J-clean if and only ifR[[x]], Hurwitz series ringH(R), trivial extensionT(R,M) andS(R,σ) are pseudo weakly J-clean, respectively. Furthermore, we prove that the following are equivalent: the ringTn(R) ofn×nupper triangular matrices overRis pseudo J-clean;QM2(R) is pseudo J-clean; For anyn∈N,Sn(R) is pseudo J-clean; For anyn∈N,R[x]/(xn) is pseudo weakly J-clean, where (xn) is the ideal generated byxn. In particular, the following conditions are equivalent:S=R[D,C] is pseudo weakly J-clean;DandCis pseudo weakly J-clean;S′=R{D,C} is pseudo weakly J-clean. Also we show that 2 is a unit inR, thenRis pseudo J-clean if and onlyRC2is pseudo J-clean.

Throughout this paper, the rings that we discussed are associative rings with an identity.Id(R) denotes the idempotents ofR,J(R) denotes the Jacobson radical ofR,U(R) denotes the unit ofRand we useTn(R) to stand for the ring of alln×nupper triangular matrices over a ringR.

2 Equivalent Characterizations

Definition 1 A ringRis called a pseudo weakly J-clean ring if every elementa∈Rcan be written in the form ofa=e+w+(1-e)Raora=-e+w+(1-e)Rawheree∈Id(R) andw∈J(R).

The ringRis said to be pseudo weakly J-clean if all of its elements are pseudo weakly J-clean.

Theorem 1 Every homomorphic image of a pseudo weakly J-clean ring is pseudo weakly J-clean.

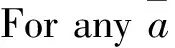
WecallaringispseudoJ-cleanifthereexistanidempotenteandaJacobsonradicalwinRsuchthata=e+w+(1-e)Raforanya∈R.

Proposition1LetRbearing.Thenthefollowingconditionsareequivalent:

1)RisapseudoJ-clean;

2)Everyelementx∈Rhastheformx=-e+w+(1-e)rxwherew∈J(R), e∈Id(R),andr∈R.

Proof1) 2).Letx∈R.SinceRispseudoJ-clean,wehave-x=w′+e+(1-e)r(-x),herew′∈J(R), e∈Id(R)andr∈R.Thenx=-w′-e+(1-e)rx.Set-w′=w,wegetx=w-e+(1-e)rx.

2) 1).Letx∈R.Then-x=-e+w+(1-e)r(-x)forsomew∈J(R), e∈Id(R)andr∈R.Wemusthavex=-w+e+(1-e)rx,because-w∈J(R),itshowsthatxispseudoJ-clean.

Theorem2ThedirectproductringR=∏k∈IRkispseudoweaklyJ-cleanifandonlyifeachRkispseudoweaklyJ-cleanandatmostoneRkisnotapseudoJ-cleanring.

Proof( ):SupposethatR=∏k∈IRkispseudoweaklyJ-clean.ByTheorem1,wecanknowthateachRkispseudoweaklyJ-cleanbecauseeachRkisahomomorphicimageofR.SupposethatRiandRj(i≠j)arenotpseudoJ-clean.SinceRiisnotpseudoJ-clean,thenbyProposition1,thereexistsxi∈Risuchthatxi≠w-e+(1-e)rxiforanyw∈J(Ri), e∈Id(Ri)andr∈Ri.ButRiisapseudoweaklyJ-cleanring,wemusthavexi=wi+ei+(1-ei)rixiforsomewi∈J(Ri), ei∈Id(Ri)andri∈Ri.NowsinceRjisnotpseudoJ-cleanbutpseudoweaklyJ-clean,thereisanxj∈Rj,wehavexj=wj-ej+(1-ej)rjxjforsomewj∈J(Rj), ej∈Id(Rj)andrj∈Rjbutxj≠w+e+(1-e)rxjforanyw∈J(Rj), e∈Id(Rj)andr∈Rj.Lety=(yk)∈Rsuchthat

Thenwegety≠w±e+(1-e)ryforanyw∈J(R), e∈Id(R)andr∈R,whichimpliesthatyisnotpseudoweaklyJ-clean;whichcontradictstheassumptionthatRispseudowealkJ-clean.Hence,wecangetatmostoneRkisnotapseudoJ-cleanring.

(?):IfeveryRiispseudoJ-clean,thisissimilartotheproofof[3,Proposition2.3]thatR=∏k∈IRkisalsopseudoJ-clean,soitispseudoweaklyJ-clean.SupposethatRi0ispseudoweaklyJ-cleanbutnotpseudoJ-cleanandalltheotherRiarepseudoJ-clean.Letx=(xi)∈R=∏k∈IRk.Thenxi0=wi0±ei0+(1-e)ri0xi0foreachxi0∈Ri0,herewi0∈J(Ri0), ei0∈Id(Ri0)andri0∈Ri0.Ifxi0=wi0+ei0+(1-e)ri0xi0,thenfori≠i0andRiispseudoJ-clean,wemusthavexi=wi+ei+(1-ei)rixiwherewi∈J(Ri), ei∈Id(Ri)andri∈Ri.Ifxi0=wi0-ei0+(1-e)ri0xi0,thenfori≠i0andRiispseudoJ-clean,thenbyProposition1thatwecanwritexi=wi-ei+(1-ei)rixiwherewi∈J(Ri), ei∈Id(Ri)andri∈Ri.Hence, x=w+e+(1-e)rxorx=w-e+(1-e)rxwherew=w(j)∈U(R), e=(ej)∈Id(R)andr=(rj)∈R.Therefore, xispseudoweaklyJ-clean.Thiscompletestheproof.

Corollary1ThedirectproductringR=∏k∈IRkispseudoJ-cleanifandonlyifeachRkispseudoJ-clean.

ProofItisobvious.

Theorem3LetRbearing.ThenRispseudoweaklyJ-cleanifandonlyifR[[x]]ispseudoweaklyJ-clean.

ProofSupposethatRispseudoweaklyJ-clean,foranya∈R,wehavea=e+w+(1-e)r(x)ora=-e+w+(1-e)r(x).Ifa=e+w+(1-e)r(x),then

f(x)= a0+a1x+a2x2+…=e+w+(1-e)ra0+(a1x+a2x2+…)=

e+w+(a1x+a2x2+…)-(1-e)r(a1x+a2x2+…)+(1-e)rf(x)=

e+α(x)+(1-e)rf(x).

Similarly,ifa=-e+w+(1-e)r(x),thenf(x)=-e+α(x)+(1-e)rf(x).Itiseasytoknowα(x)∈J(R[[x]]),hence, R[[x]]ispseudoweaklyclean.

Conversely,supposethatR[[x]]ispseudoweaklyJ-clean.ThenitfollowsbytheisomorphismR?R[[x]]/(x)andTheorem1thatRispseudoweaklyJ-clean.

Corollary2LetRbearing. R[[x1,…, xn]]ispseudoweaklyJ-cleanifandonlyifRispseudoweaklyJ-clean.

ProofByinductionandTheorem3.

Proposition2LetRbearing.ThenthepolynomialringR[x]isneverpseudoweaklyJ-cleanring.

ProofSupposethatx∈R[x]ispseudoweaklyJ-clean,thenx=e+w+(1-e)rxorx=-e+w+(1-e)rxforsomew∈J(R[x]), e∈Id(R[x])andr∈R[x].Wemaywritee=e0+e1x+…+enxnandw=w0+w1x+…+wnxnwhere(en, wn)≠(0, 0).Then

x=w+e+rx-erx=(w0+w1x+…+wnxn)+(e0+e1x+…+enxn)+rx-(e0+e1x+…+enxn)rx

or

x=w-e+rx-erx=(w0+wx1x+…+wnxn)-(e0+e1x+…+enxn)+rx-(e0+e1x+…+enxn)rx.

1=x(1+w)-1=b0x+b1x2+b2x3+…+blxl+1.

Lemma1[4]LetRbearing.ThentheHurwitzseriesx=(x0, x1, x2,…)isaunitinH(R)ifandonlyifx0isaunitinR.

Theorem4LetRbearing.ThentheHurwitzseriesx=(x0, x1, x2,…)isintheJacobsonradicalofH(R)ifandonlyifx0isintheJacobsonradicalinR.

ProofLetx=(xn)∈H(R), r=(rn)∈H(R).Ifx=(xn)∈J(H(R)),then1-ax=(1-r0x0,…)∈U(H(R)).ItfollowsfromtheLemma1,wecanknow1-r0x0∈U(R).Therefore, x0∈J(R).Conversely,ifx0∈J(R),foranyr∈R,wehave1-rx0∈U(R),therefore, 1-r0x0∈U(R).ItfollowsfromtheLemma1,wecanknow1-ax=(1-r0x0,…)∈U(H(R)).Hence, x=(xn)∈J(H(R)).

Theorem5LetRbearing.ThenH(R)ispseudoweaklyJ-cleanifandonlyifRispseudoweaklyJ-clean.

ProofByTheorem1,everyhomomorphicimageofapseudoweaklyJ-cleanringispseudoweaklyJ-clean,soR?H(R)/kerφispseudoweaklyJ-clean,whereφ:H(R)→R.

Conversely,supposethatRispseudoweaklyJ-clean.Letx=(xn)∈H(R).Thenx0∈R.Hence, x0=±e+w′+(1-e)rx0fore∈Id(R)andw′∈J(R).Thusx=λR(e)+w+λR[(1-e)rx]=(e, 0, 0,…)+w+((1-e)rx, 0, 0,…)orx=-λR(e)+w+λR[(1-e)rx]=-(e, 0, 0,…)+w+((1-e)rx, 0, 0,…),wherew∈J(H(R)).

Proposition3LetRbeapseudoJ-cleanring.Thenthefollowingstatementshold:

1)TheringTn(R)ofn×nuppertriangularmatricesoverRispseudoJ-clean;

2)QM2(R)ispseudoJ-clean;

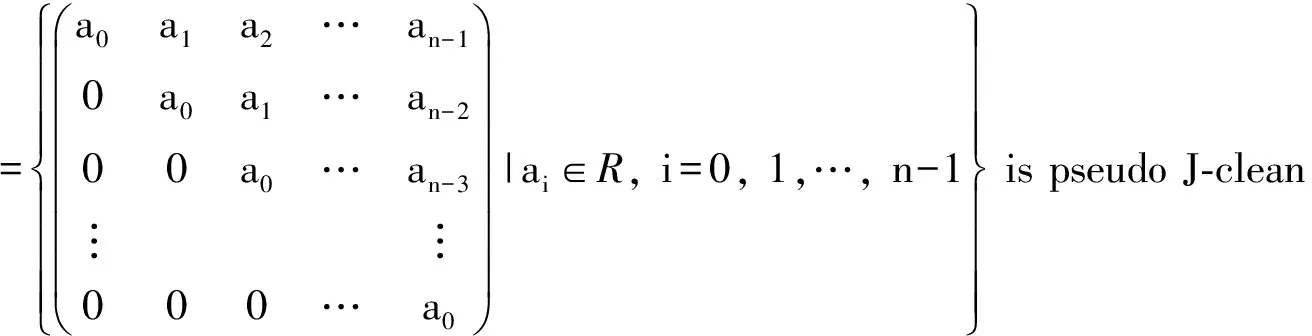
4)For anyn∈N,R[x]/(xn) is pseudo J-clean, where (xn) is the ideal generated byxn.

3)Theproofissimilartothatof1).

4)NotethatR[x]/(xn)?Sn(R),weobtaintheresultby3).

GivenaringRanda(R, R)-bimoduleM,thetrivialextensionofRbyMistheringT(R, M)=R⊕Mwiththeusualadditionandthefollowingmultiplication: (r1, m1)(r2, m2)=(r1r2, r1m2+m1r2).AsweallknowJ(R×M)={(r, m)|r∈J(R), m∈RMR}.

Proposition4LetRbearing.ThenRispseudoweaklyJ-cleanifandonlyifT(R, M)ispseudoweaklyJ-clean.

ProofIfRisweaklyJ-clean,forany(x, m)∈T(R, M)sinceRisweaklyJ-clean, x=e+w+(1-e)rxorx=-e+w+(1-e)rx,wheree∈Id(R), w∈J(R).Wehave(x, m)=(e+w+(1-e)rx, m)or(x, m)=(-e+w+(1-e)rx, m).Hence(x, m)=(e, 0)+(w, m)+((1-e)rx, 0)or(x, m)=-(e, 0)+(w, m)+((1-e)rx, 0)where(e, 0)∈Id(T(R, M))and(w, m)∈J(T(R, M)),soT(R, M)ispseudoweaklyJ-clean.

Conversely,ifT(R, M)ispseudoweaklyJ-clean,foranyx∈R, (x, 0)∈T(R, M),wehave(x, 0)=(e, *)+(w, *)+((1-e)rx, 0)or(r, 0)=-(e, *)+(w, *)+((1-e)rx, 0)where(e, *)2=(e2, *)=(e, *)and(w, *)∈J(T(R, M))thatisx=e+w+(1-e)rxorx=-e+w+(1-e)rxwheree∈Id(R)andw∈J(R),soRispseudoJ-weakly.

Theorem 6 LetRbe a ring. ThenRis pseudo weakly J-clean if and only ifS(R,σ) is pseudo weakly J-clean.

3 Related Rings

Inthissection,wefurtherconsiderpseudoweakJ-cleannessofvariousrelatedrings.WenowconsidertheconnectionofpseudoweakJ-cleannessandweakJ-cleanness.

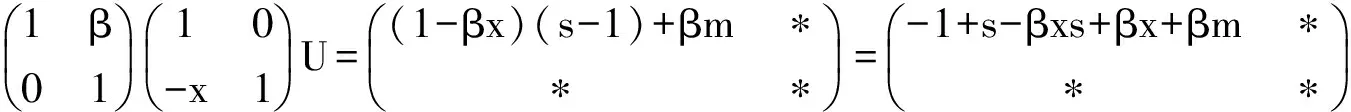
Letu=α+βγa=-1+s-βxs+βx+βm∈-1+J(R).Thensubstitutingα=u-βγaintotheequationαa=fα+1,weget

ua-βγa2= f(u-βγa)+1=fu+1 u-1(ua-βγa2)=u-1(fu+1)

a-u-1βγa2=u-1fu+u-1a-u-1fu-u-1=u-1βγa2.

Wesetu-1=-1+w′, w′∈J(R),itfollowsthat

a-u-1fu-(-1+w′)-u-1βγ= u-1βγ(a-1)(a+1)

a+1-u-1fu-(w′+u-1βγ)=u-1βγ(a-1)(a+1).

Fromtherelationfβ=0,wecanknowβ=eβ.Wehave

a+1-u-1fu-(w′+u-1βγ)= u-1eβγ(a-1)(a+1)=u-1eu(u-1βγ)(a-1)(a+1)=

(1-u-1fu)(u-1βγ)(a-1)(a+1)∈(1-u-1fu)R(a+1).

Setu-1fu=g1∈Id(R), w1=w′+u-1βγ∈J(R),andweknowb=a+1,sob-g1-w1∈(1-g1)Rb,asdesired.

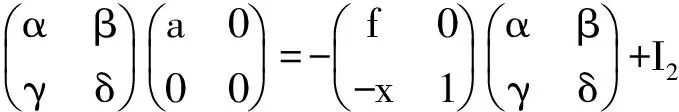
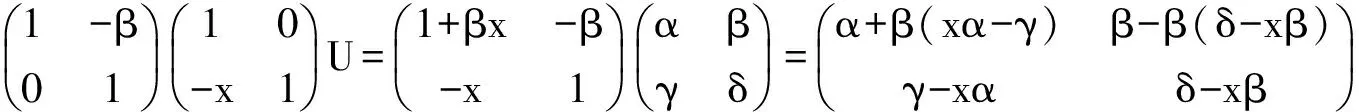
Letv=α+βγaandbyusingsimilartothoseabove,wecanknowv=α+βγa=-1+s+βxs-βx-βm∈-1+J(R)andwesetv-1=-1+w″, w″∈J(R),itfollowsthat

a+v-1fv-(-1+w″)-v-1βγ= v-1βγ(a-1)(a+1)

a+1+v-1fv-(w″+v-1βγ)=v-1βγ(a-1)(a+1).

Fromtherelationfβ=0,wecanknowβ=eβ.Wehave

a+1+v-1fv-(w″+v-1βγ)= v-1eβγ(a-1)(a+1)=v-1ev(v-1βγ)(a-1)(a+1)=

(1-v-1fv)(v-1βγ)(a-1)(a+1)∈(1-v-1fv)R(a+1).

Setv-1fv=g2∈Id(R), w2=w″+v-1βγ∈J(R),andweknowb=a+1,sob+g2-w2∈(1-g2)Rb,asdesired.

LetDbearing, CbeasubringofDand1D∈C,write:

S=R[D, C]={(d1,…, dn, c, c,…)|di∈D, c∈C, n≥1},

S′=R{D, C}={(d1,…, dn, cn+1, cn+2,…)|di∈D, cj∈C, n≥1}.

Here, the addition and multiplication are defined componentwise, bothS=R[D,C] andS=R{D,C} are rings with identities.

Lemma 2 1)J(S)=R[J(D),J(D)∩J(C)];

2)J(S′)=R{J(D),J(D)∩J(C)}.

Proof See [5, Proposition 2.1.14].

Theorem 8 LetS=R[D,C]. Then the following conditions are equivalent:

1)S=R[D,C] is pseudo weakly J-clean;

2)Dis pseudo weakly J-clean and for anya∈C, there existw∈J(D)∩J(C),e∈Id(C), such thata-w±e∈(1-e)Ca;

3)S′=R{D,C} is pseudo weakly J-clean.

3)?2).Itissimilarto1)?2).

GivenagroupGandaringA,thegroupringR=AG,consistsofallfunctionsr:G→Awithfinitesupport.Thesupportofris{g∈G|r(g)≠0}. Risendowedwithringoperationbydefining:

Let us verify thatR(0, 1, -, +, ·) is in fact a ring.

We first consider some cases where a group ring is isomorphic (as a ring) to a direct product of copies of the coefficient ring.

Proposition 5 LetRbe a ring and let 2 be a unit inR. ThenRis pseudo J-clean if and only ifRC2is pseudo weakly J-clean.

Proof LetC2={x|x2=1} and defineφ:RC2→R×Rbyφ(a+bx)=(a+b,a-b) wherea,b∈R. Thenψis a ring homomorphism. Since 2 is a unit inR, we have thatψis bijective. Therefore,RC2?R×R. IfRis pseudo J-clean, it follows by Corollary 1 thatRC2?R×Ris pseudo weakly J-clean; Conversely, ifRC2?R×Ris pseudo weakly J-clean, it follows by Theorem 1 thatR×Ris pseudo weakly J-clean. Therefore,Ris pseudo J-clean by Theorem 2.

Proposition 6 LetRbe a ring and let 2 be a unit inR. ThenRis pseudo J-clean if and only ifRC2is pseudo J-clean.

Proof As in the proof of Proposition 5, it may be shown thatRC2?R×R. It then follows by Corollary 1 thatRis pseudo J-clean if and only ifRC2is pseudo J-clean.

By Proposition 5 and Proposition 6 we have the following.

Corollary 3 LetRbe a ring and let 2 be a unit inR. Then the following are equivalent:

1)Ris pseudo J-clean;

2)RC2is pseudo weakly J-clean;

3)RC2is pseudo J-clean.

Proposition 7 LetRbe a ring and let 2 be a unit inR. Then the following are equivalent:

1)Ris pseudo J-clean;

3) 2). It is obvious.

[1] QUA K T. Weakly clean and related rings[D]. Kuala Lumpur: The University of Malaya,2015.

[2] CHEN H Y. On strongly J-clean rings[J]. Comm Algebra,2010,38(10):3790-3804.

[3] STER J. Weakly clean rings[J]. J Algebra,2014,401(401):1-12.

[4] KEIGHER W F. On the ring of Hurwize series[J]. Comm Algebra,1997,25(25):1845-1859.

[5] CHENG G P. The structure of ringR[D,C] and its characterizations[D]. Nanjing: Nanjing University,2006.

HU Xiaomei, CHEN Huanyin

(School of Science, Hangzhou Normal University, Hangzhou 310036, China)

一個環(huán)R叫做 pseudo weakly J-clean 環(huán),如果R中的每一個元素都可以寫成a=e+w+(1-e)Ra或a=-e+w+(1-e)Ra的形式,其中e是冪等元,w屬于Jacobson根.文章探究了pseudo weakly J-clean環(huán)的各種性質(zhì).環(huán)R是pseudo weakly J-clean環(huán)當且僅當冪級數(shù)環(huán)R[[x]], Hurwitz級數(shù)環(huán)H(R),平凡擴張T(R,M)和S(R,σ)分別是pseudo weakly J-clean環(huán).更進一步證明以下幾點是等價的：任意的n∈N,Sn(R)是 pseudo J-clean;任意的n∈N,R[x]/(xn)是pseudo J-clean, (xn)是由xn生成的理想.特別的,闡述了在某種條件下S=R[D,C]是pseudo weakly J-clean;并且得出結(jié)論：當2是R中的可逆元時,R是pseudo J-clean當且僅當群環(huán)RC2是pseudo J-clean.

pseudo weakly J-clean環(huán)；Hurwitz級數(shù)環(huán)；S=R[D,C]環(huán)；群環(huán)；Jacobson根；冪等元

關(guān)于Pseudo Weakly J-clean環(huán)

胡小美, 陳煥艮

(杭州師范大學理學院, 浙江 杭州 310036)

Foundation item：Supported by the Natural Science Foundation of Zhejiang Province(LY17A010018).

CHEN Huanyin(1963—), male, Professor, Ph.D., majored in algebra of basic mathematics.E-mail:huan- yinchen@aliyun.com

10.3969/j.issn.1674-232X.2016.06.012

O153.3 MSC2010: 13F25; 16S34; 16U10 Article character: A

1674-232X(2016)06-0623-09

Received date：2016-02-06