全變換半群X中的局部子半群

葉碩海，楊秀良

(杭州師范大學理學院，浙江 杭州 310036)

?

葉碩海，楊秀良

(杭州師范大學理學院，浙江 杭州 310036)

全變換半群;冪等元;局部子半群

另外,設S為任意一個半群,e為S中的冪等元,則由文獻[3]知S中的非空子集eSe關于S上的運算構成半群S的一個子半群,并且稱S中形如eSe的子半群為半群S的局部子半群.

關于半群S中的局部子半群,人們通常會問:當S滿足某些性質時,它的局部子半群是否也滿足這些性質.例如當S為一個群,e為S中的單位元(也是唯一的冪等元)時,則eSe=S自然也為一個群.又如在文獻[3]中,Howie說明了若S為正則半群,則其任一個局部子半群也正則.而文獻[4]對半群的局部性質做出了進一步的討論(在一個半群S中,若S的一個性質P滿足S中的所有局部子半群也具備這個性質P,則稱P為S的局部性質).而對于局部子半群的其他性質,可參考文獻[5-6].

1 主要結果

2 兩個引理

在證明定理1之前還需兩個引理.

1)e為冪等元;

2)e限制在im(e)上為im(e)上的恒等映射;

證明 1) 2).對任意的y∈im(e),首先存在x∈X使得y=e(x),從而e(y)=e(e(x))=e2(x)=e(x)=y,因此e限制在im(e)上為im(e)上的恒等映射.

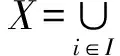
1.5統計學分析 運用SPSS15.0軟件進行統計學分析,計數資料采用X2檢驗,計量資料采用t檢驗,P<0.05表示具有統計學意義。

下面來說明ai∈Ai.這是因為對任意的i∈I,首先有ai∈im(e),而e限制在im(e)上為恒等映射,因而馬上有e(ai)=ai,因此ai∈e-1(ai)=Ai.

對任意的x∈X,由于X=∪i∈IAi,從而存在唯一的k∈I滿足x∈Ak,從而按Ak的定義馬上有e(x)=ak.又由于ak∈Ak,因而又有e(ak)=ak,從而e2(x)=e(e(x))=e(ak)=ak=e(x).再由x的任意性便知e2=e,即e為冪等元.

1)im(α)?im(e);

2)對任意的a,b∈X,若存在k∈I使得a,b∈Ak,則必有α(a)=α(b).

3 定理1的證明

δ(Ak)=yk.故對任意的k∈I,α(Ak)=xk=aα～(k)=a(k)=yk=δ(Ak).因此α=δ.

□

4 定理1的推論

特別地,當X=N={1,2,…,n}為有限集合時,便有下面結論.

□

證明 設im(e)={ai}i∈I以及im(f)={bj}j∈J,其中I,J均為非空指標集.

□

[1] HOWIE J M. An introduction to semigroup theory[M]. London: Academic Press,1976:1-13.

[2] GANYUSHKIN O, MAZORCHUK V. Introduction to classical finite transformation semigroups[M]. London: Springer Verlag,2009:19-39.

[3] HOWIE J M. Fundamentals of semigroup theory[M]. New York: Oxford University Press,1995:223-226.

[4] HALL T E. Some properties of local subsemigroups inherited by larger subsemigroups[J]. Semigroup Forum,1982,25(1):35-49.

[5] MAGILL K, MISRA P R. Principal continuum congruences, regularγ-classes and local subsemigroups[J]. Semigroup Forum,1990,40(1):205-226.

[6] MAGILL K, MISRA P R. Ordering the local subsemigroups of a semigroup[J]. Semigroup Forum,1986,35(1):101-117.

YE Shuohai, YANG Xiuliang

(School of Science, Hangzhou Normal University, Hangzhou 310036, China)

full transformation semigroup; idempotent; local subsemigroup

2016-01-06

楊秀良(1963—)，男，教授，主要從事半群代數研究.E-mail：yxl@hznu.edu.cn

10.3969/j.issn.1674-232X.2016.06.017

O152.7 MSC2010: 43A22

A

1674-232X(2016)06-0656-03