高階矩量法中幾何結(jié)構(gòu)及波端口對(duì)稱性分析

李艷艷，左 勝，王 永，張 玉

(西安電子科技大學(xué) 天線與微波技術(shù)重點(diǎn)實(shí)驗(yàn)室，陜西 西安 710071)

?

高階矩量法中幾何結(jié)構(gòu)及波端口對(duì)稱性分析

李艷艷，左 勝，王 永，張 玉

(西安電子科技大學(xué) 天線與微波技術(shù)重點(diǎn)實(shí)驗(yàn)室，陜西 西安 710071)

針對(duì)幾何結(jié)構(gòu)及波端口激勵(lì)源對(duì)稱的大型目標(biāo)， 給出了高階矩量法結(jié)合波端口理論的對(duì)稱性分析方法. 結(jié)合并行核外計(jì)算技術(shù)， 分析了大型波導(dǎo)窄邊縫隙陣列的輻射特性． 數(shù)值結(jié)果表明， 利用波導(dǎo)縫隙陣列的幾何結(jié)構(gòu)對(duì)稱性結(jié)合波端口的對(duì)稱性，能夠在保證算法精度的同時(shí)大幅度降低矩量法的內(nèi)存需求和計(jì)算時(shí)間．

高階矩量法;波端口;對(duì)稱性;大型波導(dǎo)縫隙陣

近年來(lái)，隨著對(duì)雷達(dá)抗干擾要求的提高和脈沖多普勒可視雷達(dá)的發(fā)展， 要求天線具有較高的增益和較低的副瓣， 使得天線的單元數(shù)目和電尺寸不斷增大， 因此，大型天線陣電磁輻射特性的精確分析越來(lái)越重要． 隨著天線陣列規(guī)模的不斷增大， 所需消耗的資源急劇上升， 大型天線陣列的整體仿真已成為目前的一大難題． 矩量法(Method of Moment，MoM)作為目標(biāo)電磁特性仿真計(jì)算中最精確的數(shù)值方法[1]， 在分析復(fù)雜電大目標(biāo)時(shí)會(huì)產(chǎn)生龐大的復(fù)數(shù)稠密矩陣， 計(jì)算機(jī)資源的限制是其主要的應(yīng)用瓶頸， 尤其對(duì)于傳統(tǒng)的低階RWG(Rao-Wilton-Glisson)矩量法． 為突破這一瓶頸， 通常可采用基于高階多項(xiàng)式基函數(shù)， 它能更好地?cái)M合物體表面電磁流分布， 將矩量法對(duì)模型網(wǎng)格邊長(zhǎng)的要求放松到1個(gè)波長(zhǎng)左右， 可大大降低矩量法矩陣規(guī)模． 波導(dǎo)縫隙天線陣是一種比較常見(jiàn)的采用波端口激勵(lì)的問(wèn)題， 筆者課題組前期工作即采用并行高階矩量法結(jié)合波端口理論進(jìn)行了波導(dǎo)縫隙天線的建模分析[2]．

當(dāng)陣列規(guī)模變得更大時(shí)，對(duì)計(jì)算資源的需求也會(huì)隨之增大，高階矩量法結(jié)合波端口分析復(fù)雜大型波導(dǎo)縫隙陣列的能力也會(huì)受到限制．針對(duì)這一問(wèn)題，筆者進(jìn)一步研究了關(guān)于波端口理論的對(duì)稱性，給出了一種基于并行高階矩量法的波端口對(duì)稱性分析方法．該方法充分利用多數(shù)典型天線陣列所具有的幾何結(jié)構(gòu)和激勵(lì)源的對(duì)稱性，將所求解的問(wèn)題計(jì)算規(guī)模至少縮小為原問(wèn)題的 1/2，甚至縮小為原問(wèn)題的 1/8，極大地減少了所求解目標(biāo)的未知量數(shù)目，求解時(shí)間和存儲(chǔ)量也會(huì)相應(yīng)降低．因此，利用現(xiàn)有的計(jì)算機(jī)資源就可精確分析大型天線陣列的電磁特性．同時(shí)，還采用了一種核外求解技術(shù)，將“硬盤”存儲(chǔ)動(dòng)態(tài)地納入矩量法計(jì)算過(guò)程， 從而打破計(jì)算機(jī)內(nèi)存的限制[3]． 此外， 可利用大規(guī)模并行計(jì)算技術(shù)進(jìn)一步提高矩量法的計(jì)算規(guī)模和計(jì)算速度． 文中通過(guò)對(duì)X波段波導(dǎo)縫隙雙面天線陣的輻射特性分析， 證明了該方法可極大降低矩量法的資源需求和計(jì)算時(shí)間， 且不會(huì)帶來(lái)計(jì)算精度的損失． 并給出一個(gè)實(shí)際應(yīng)用的Ka波段大型波導(dǎo)縫隙天線陣的數(shù)值分析， 仿真結(jié)果表明，該方法能夠有效應(yīng)用于具有對(duì)稱性結(jié)構(gòu)的大型波導(dǎo)縫隙天線陣列的綜合仿真．

1 幾何結(jié)構(gòu)與波端口的對(duì)稱性

高階矩量法采用高階基函數(shù)和雙線性面片來(lái)逼近真實(shí)的電流分布， 自動(dòng)滿足連續(xù)性方程， 保證了金屬介質(zhì)連接區(qū)域的電磁流連續(xù)性， 具體介紹參見(jiàn)文獻(xiàn)[3-4]． 高階基函數(shù)對(duì)網(wǎng)格邊長(zhǎng)的要求放松到1個(gè)波長(zhǎng)左右， 一般描述1平方波長(zhǎng)目標(biāo)的電磁流只需大約20個(gè)基函數(shù)， 是低階矩量法的約 1/5．

圖1 波端口等效問(wèn)題模型

運(yùn)用Love場(chǎng)等效原理構(gòu)造一個(gè)計(jì)算波導(dǎo)內(nèi)部區(qū)域(區(qū)域Ⅱ)場(chǎng)的等效模型． 此時(shí)假設(shè)除區(qū)域Ⅱ外， 其余區(qū)域電場(chǎng)、磁場(chǎng)分布均為0， 記作(0， 0)， 用區(qū)域Ⅱ的媒質(zhì)代替其他區(qū)域的媒質(zhì)， 如圖1(b)所示．

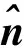
接下來(lái)運(yùn)用Love場(chǎng)等效原理，構(gòu)造一個(gè)計(jì)算波端口連接的半無(wú)限長(zhǎng)波導(dǎo)(區(qū)域Ⅰ)場(chǎng)的等效模型． 此時(shí)，假設(shè)除區(qū)域Ⅰ外， 其余區(qū)域場(chǎng)填充理想導(dǎo)體．

為保持邊界條件不變，需在端口的表面Sd上強(qiáng)加等效電磁流JⅠ和MⅠ， 則Sd上滿足的邊界條件為

對(duì)于等效問(wèn)題， 必須保持邊界條件滿足原問(wèn)題的邊界條件， 因此，有

具體分析過(guò)程詳見(jiàn)文獻(xiàn)[6]．

區(qū)域Ⅱ中的場(chǎng)可表示為等效源的積分形式，即

EⅡ=EⅡ(J0, M0, J)=ηⅡL(J0)-K(M0)+ηⅡ

女兒走了，蘇母埋怨蘇穆武：有你那么說(shuō)話的嗎？蘇穆武不服地：我怎么說(shuō)話了？找個(gè)洋人當(dāng)女婿我不同意！蘇母說(shuō)：找什么女婿是閨女自己的事，你上那么大火干啥？蘇穆武提高聲音：什么叫她自己的事？她是從鞋旮旯里蹦出來(lái)的？蘇母斥責(zé)他：別說(shuō)那么難聽(tīng)好不好，我看這事咱也考慮考慮。蘇穆武脖子一擰：沒(méi)啥考慮的，不同意就不同意！我真不明白，張陽(yáng)有禮貌又懂事，她怎么就看不上？蘇母無(wú)奈地：這你得去問(wèn)你閨女。蘇穆武說(shuō)：不用問(wèn)我也知道！蘇母問(wèn)：你知道什么？蘇穆武鼻子一哼：女人就是犯賤！

區(qū)域Ⅰ內(nèi)的電磁場(chǎng)是入射場(chǎng)、全反射場(chǎng)和磁流-M0產(chǎn)生的場(chǎng)的疊加． 總場(chǎng)為

其中，bi為未知系數(shù)，ej為電場(chǎng)．

最后，可得到積分方程為

依此方法可給出任意N端口波導(dǎo)情形下的積分方程． 這里需要指出的是， 矩量法求解方程式(7)時(shí)， 均采用高階基函數(shù)作為基函數(shù)和檢驗(yàn)函數(shù)， 這樣可大幅度降低求解目標(biāo)的未知量， 進(jìn)一步擴(kuò)大矩量法求解問(wèn)題的規(guī)模．

工程應(yīng)用中大型天線陣在結(jié)構(gòu)上通常都具有對(duì)稱性， 這就意味著可采用對(duì)稱性方法來(lái)分析天線陣的電磁特性， 即將其中1個(gè)或幾個(gè)對(duì)稱單元看作是某一個(gè)單元的鏡像源， 這樣在計(jì)算過(guò)程中只需要構(gòu)造出一半甚至更小的幾何模型， 就可求解整個(gè)目標(biāo)的場(chǎng)．針對(duì)對(duì)稱性分析方法， 幾何結(jié)構(gòu)的對(duì)稱是所有對(duì)稱的前提， 源分布的對(duì)稱決定對(duì)稱面的類型， 即電壁或磁壁．

文中主要介紹波端口的對(duì)稱性， 其他激勵(lì)形式比較簡(jiǎn)單， 這里不作討論． 矩形波端口是一種比較常見(jiàn)的波端口形式， 通常有3種幾何對(duì)稱結(jié)構(gòu)， 如圖2(a)所示．

圖2 波端口的對(duì)稱性

若對(duì)稱面為磁壁，則平行于對(duì)稱面的電流同向， 垂直于對(duì)稱面的電流反向；若對(duì)稱面為電壁， 則相反． 這里以目標(biāo)具有兩個(gè)對(duì)稱面且對(duì)稱面為磁壁的情形為例進(jìn)行分析， 如圖2(b)所示． 矩量法矩陣方程可表示為

其中，Zij(i=j)為第i個(gè)區(qū)域?qū)ΨQ結(jié)構(gòu)的自阻抗矩陣， Zij(i≠j) 為第i個(gè)區(qū)域與第j個(gè)區(qū)域?qū)ΨQ結(jié)構(gòu)之間的互阻抗矩陣． 由于幾何結(jié)構(gòu)完全對(duì)稱， 根據(jù)矩量法阻抗矩陣填充過(guò)程可知，Z11= Z22= Z33= Z44， Z12= Z21， Z13= Z31， Z14= Z41， Z23= Z32， Z24= Z42， Z34= Z43， Z13= Z24， Z14= Z23．根據(jù)源分布的對(duì)稱性可知，V1= V2= V， V3= V4= -V，可得，I1= I2= -I3= -I4． 則式(8)可寫為

求解矩陣方程式(9)得到電流I1．值得注意的是，波導(dǎo)的輻射場(chǎng)是4個(gè)部分的表面電流產(chǎn)生的場(chǎng)的疊加， 即

其中，ηⅢ=(μⅢεⅢ)1/2，為區(qū)域Ⅲ中的波阻抗．

2 數(shù)值算例

2.1 X波段雙面波導(dǎo)縫隙陣列輻射特性

此處以X波段波導(dǎo)窄邊縫隙天線雙面陣列的輻射特性計(jì)算為例[7-8]， 來(lái)驗(yàn)證并行核外高階矩量法采用波端口對(duì)稱性時(shí)的準(zhǔn)確性． 如圖3(a)所示， 仿真模型是兩個(gè)由10根波導(dǎo)縫隙天線組成的雙面天線陣列， 天線的幾何結(jié)構(gòu)和激勵(lì)源均關(guān)于兩個(gè)面對(duì)稱． 單根波導(dǎo)的尺寸為 22.86 mm× 10.16 mm× 266.58 mm， 縫隙個(gè)數(shù)為10個(gè)． 每根波導(dǎo)均采用波端口激勵(lì)， 工作頻率為 9.375 GHz， 泰勒綜合設(shè)計(jì)的副瓣電平為 -35 dB． 采用對(duì)稱性與整體求解得到天線陣列的二維增益方向圖如圖4所示．為進(jìn)一步驗(yàn)證該方法的準(zhǔn)確性， 同時(shí)也給出了RWG低階矩量法的仿真結(jié)果． 從圖中可以看出，3種方法的仿真結(jié)果吻合良好． 本算例采用RWG低階矩量法整體解未知量為 248 792， 而高階矩量法整體解未知量為 63 960， 高階矩量對(duì)稱性解未知量?jī)H為 15 990． 可以得出，該方法能夠大幅度降低求解問(wèn)題的規(guī)模， 并能快速準(zhǔn)確分析大型波導(dǎo)縫隙天線陣的輻射特性．

圖3 波導(dǎo)縫隙天線陣列仿真模型

圖4 波導(dǎo)縫隙天線陣列的增益方向圖

2.2 Ka波段波導(dǎo)縫隙陣列的輻射特性

利用對(duì)稱性求解一個(gè)Ka波段大型波導(dǎo)縫隙陣列的輻射特性， 來(lái)表明波端口對(duì)稱性在實(shí)際電磁工程應(yīng)用中的有效性． Ka波段波導(dǎo)縫隙陣列的整體仿真模型和加對(duì)稱面仿真模型如圖5所示． 陣列由22根波導(dǎo)縫隙天線組成， 工作頻率為 35 GHz， 每根波導(dǎo)均采用波端口激勵(lì)， 泰勒綜合設(shè)計(jì)陣列副瓣電平為 -35 dB[9]． 高階矩量法產(chǎn)生的未知量為 583 478， 此時(shí)如果采用低階RWG矩量法幾乎無(wú)法求解． 本例中利用陣列幾何結(jié)構(gòu)和激勵(lì)的對(duì)稱性， 所需求解的問(wèn)題規(guī)模變?yōu)榍蠼庠瓎?wèn)題的 1/2， 即未知量減少到 291 739．

圖5 大型波導(dǎo)縫隙陣列的仿真模型

采用對(duì)稱性與整體求解兩種方式計(jì)算波導(dǎo)縫隙天線陣的增益方向圖如圖6所示， 從圖6可看到兩種方式計(jì)算結(jié)果吻合良好． 此外， 表1給出了兩種求解方式所消耗的計(jì)算資源和計(jì)算時(shí)間． 可以得出， 采用對(duì)稱性分析， 陣列的未知量變?yōu)樵瓎?wèn)題的 1/2， 求解所需的存儲(chǔ)量由 4.95 TB 降到了 1.24 TB， 使用相同CPU核數(shù)的計(jì)算時(shí)間由 11.6 h 降到了 2.1 h， 這充分體現(xiàn)了對(duì)稱性求解在計(jì)算資源和計(jì)算時(shí)間方面的優(yōu)勢(shì)．

圖6 大型波導(dǎo)縫隙陣列的增益方向圖

高階矩量法未知量存儲(chǔ)量/TB進(jìn)程數(shù)時(shí)間/s整體求解58347849512004186030對(duì)稱性求解2917391241200772464

3 結(jié) 束 語(yǔ)

針對(duì)雷達(dá)天線系統(tǒng)中常用的大型波導(dǎo)縫隙陣列， 提出了并行核外高階矩量法的波端口對(duì)稱性． 該方法在保證算法精度的同時(shí)， 可大幅度降低模型產(chǎn)生的未知量， 進(jìn)而降低了計(jì)算所需資源， 減少了計(jì)算所需時(shí)間．?dāng)?shù)值結(jié)果表明， 利用波端口的對(duì)稱性可快速精確地分析具有對(duì)稱性結(jié)構(gòu)的大型波導(dǎo)縫隙天線陣列的輻射特性．

[1] HARRINGTON R F. Field Computation by Moment Methods [M]. New York: IEEE Press, 1993.

[2]WANG Y, ZHAO X W, ZHANG Y, et al. Higher-order MoM Analysis of Traveling-wave Waveguide Antennas with Matched Waveports [J]. IEEE Transactions on Antennas and Propagation, 2015, 63(8): 3718-3721.

[3] ZHANG Y, SARKAR T K. Parallel Solution of Integral Equation Based EM Problems in the Frequency Domain [M]. Hoboken: Wiley-IEEE Press, 2009.

[4]ZHANG Y, SARKAR T K, ZHAO X, et al. Higher Order Basis Based Integral Equation Solver (HOBBIES) [M]. Hoboken: John Wiley, 2012.

[5]BUNGER R, ARNDT F. Moment-method Analysis of Arbitrary 3-D Metallic N-port Waveguide Structures [J]. IEEE Transactions on Microwave Theory and Techniques, 2000, 48(4): 531-537.

[6]王 永, 林中朝, 張 玉, 等. 并行矩量法分析波導(dǎo)縫隙天線的輻射特性 [J]. 西安電子科技大學(xué)學(xué)報(bào), 2015, 42(5): 84-90.

WANG Yong, LIN Zhongchao, ZHANG YU, et al. Analysis of the Radiation of Slotted Waveguide Antennas Using Parallel MoM [J]. Journal of Xidian University, 2015, 42(5): 84-90.

[7]李建瀛, 梁昌洪. 波導(dǎo)窄邊縱縫的理論分析及頻掃縫陣 [J]. 西安電子科技大學(xué)學(xué)報(bào), 1998, 25(5): 689-692.

LI Jianying, LIANG Changhong. Theoretical Analysis of the Longitudinal Slot in the Narrow Wall of a Rectangular Waveguide and Frequency Scan Array [J]. Journal of Xidian University, 1998, 25(5): 689-692.

[8]KUMAR P, KEDAR A, SINGH A K. Design and Development of Low-cost Low Sidelobe Level Slotted Waveguide Antenna Array in X-band [J]. IEEE Transactions on Antennas and Propagation, 2015, 63(11): 4723-4731.

[9]VOLAKIS J L, GILBERT R A. Antenna Engineering Handbook [M]. New York: McGraw-Hill Education, 2007.

(編輯：齊淑娟)

Analysis of the geometry and wave port symmetry in the higher-order MoM

LIYanyan，ZUOSheng，WANGYong，ZHANGYu

(Science and Technology on Antennas and Microwave Lab., Xidian Univ., Xi’an 710071, China)

Focusing on the symmetry of the geometric structure and wave port excitation, a symmetric analysis method utilizing the combination of the higher-order MoM and wave port theory is proposed. With the help of the parallel out-of-core computing technique, the radiation characteristics of a large-scale narrow slotted waveguide array are simulated. Numerical results show that the using the wave port and geometric symmetry can significantly reduce the requirement of memory and computing time while maintaining the same precision and accuracy.

higher-order MoM; wave port; symmetry; large waveguide slotted array

2015-11-10

時(shí)間：2016-04-01

國(guó)家高技術(shù)研究發(fā)展計(jì)劃(863計(jì)劃)資助項(xiàng)目(2012AA01A308)；國(guó)家自然科學(xué)基金資助項(xiàng)目(61301069, 61072019)；教育部新世紀(jì)優(yōu)秀人才支持計(jì)劃資助項(xiàng)目(NCET-13-0949)；陜西省青年科技新星資助項(xiàng)目(2013KJXX-67)；中央高校基本科研業(yè)務(wù)費(fèi)重點(diǎn)資助項(xiàng)目(JY10000902002)

李艷艷(1988-)，女，西安電子科技大學(xué)博士研究生，E-mail：yuseexidian@163.com．

http://www.cnki.net/kcms/detail/61.1076.tn.20160401.1622.012.html

10.3969/j.issn.1001-2400.2016.06.006

TN820

A

1001-2400(2016)06-0034-05