基于滑模的圓筒直線電機位置控制系統研究

夏 俊，李倩龍，潘劍飛，張 博

(1.深圳市電子學會，深圳 518052；2.深圳電磁控制重點實驗室，深圳 518060)

?

基于滑模的圓筒直線電機位置控制系統研究

夏 俊1，李倩龍2，潘劍飛2，張 博2

(1.深圳市電子學會，深圳 518052；2.深圳電磁控制重點實驗室，深圳 518060)

無鐵心圓筒直線電機具有重量輕、慣性小、響應速度快等優點，廣泛應用于工業加工及制造領域。由于此類控制系統易受參數變化和負載擾動等不確定因素的影響，且傳統比例-積分-微分(PID)控制器難以保證此類被控對象快速性和穩態性能的缺點，采用基于指數趨近律的滑模算法，縮短滑模變量的趨近時間，從而提高該直線電機位置控制系統的響應速度。實驗結果表明，該方法使無鐵心圓筒直線電機位置控制系統同時具有響應速度快和穩態性能高的優勢，在幅值為10 mm,頻率為0.5 Hz方波參考位置信號下，上升時間不超過29 ms，絕對穩態誤差精度控制不超過3 μm。

無鐵心圓筒直線電機；滑模；位置控制；趨近律

0 引 言

作為直驅直線電機的一種，圓筒型直線電機可以直接驅動負載作直線運動，無需旋轉電機配合機械傳動裝置轉變成直線運動。這類直線電機具有響應速度高、損耗低等優點，在響應速度快及高精度的直線交流伺服系統中獲得廣泛應用[1]。圓筒直線電機從結構上分為有鐵心圓筒直線電機和無鐵心圓筒直線電機(Ironless Tubular Permanent Magnet Linear Motor, ITPMLM)，與有鐵心圓筒直線電機相比，ITPMLM重量輕、慣性小、運行噪音更低，不存在齒槽效應以及鐵心兩端開端引起的推力波動問題[1]。但模型參數的非確定性及外部的干擾等因素增加了控制難度。采用傳統PID控制器一般可以使控制系統獲得較好的魯棒特性和控制效果，由于圓筒型直線電機這類被控對象模型對控制參數敏感，因此，系統的快速性以及穩態性能很難同時兼顧[2]。文獻[3]采用直接推力方法設計的系統控制器，該控制方法舍去矢量旋轉變換等復雜運算，使控制系統計算簡化，從而提高系統的快速響應能力。但該方法具有電壓矢量不連續造成的磁鏈脈動及低速運行性能差等問題。文獻[4]采用基于指數趨近律滑模控制方案進行仿真分析，該方法使控制系統具有較快的響應速度和較好的魯棒性，但并未搭建實驗平臺得出實驗結果，也沒有分析系統的響應性能。

本文采用基于指數趨近律的滑模控制方法設計位置控制器，搭建實驗平臺，并與傳統PID控制器實驗結果相比，滑模控制器下位置跟蹤響應速度、收斂速度以及穩態精度都有所提高。

1 電機結構

被控對象是Copley公司生產的SM1104型ITPMLM。ITPMLM實物圖如圖1所示，其主要由基座、導軌、定子桿、動子以及位置傳感器等組成。圖2為ITPMLM沿定子桿軸線1/4剖面結構示意圖，其中動子由繞組和繞組支架組成，繞組支架采用環氧樹脂材料塑封而成。定子由永磁體和不銹鋼管組成，永磁體采用稀土材料釹鐵硼制作而成，軸向充磁；極性相反依次排列。動子和定子之間有一定氣隙。該電機的結構為4極6槽，極距為25.6 mm，可得電機對應的槽距為17.07 mm。表1為電機的主要結構參數。

圖1 ITPMLM實物圖

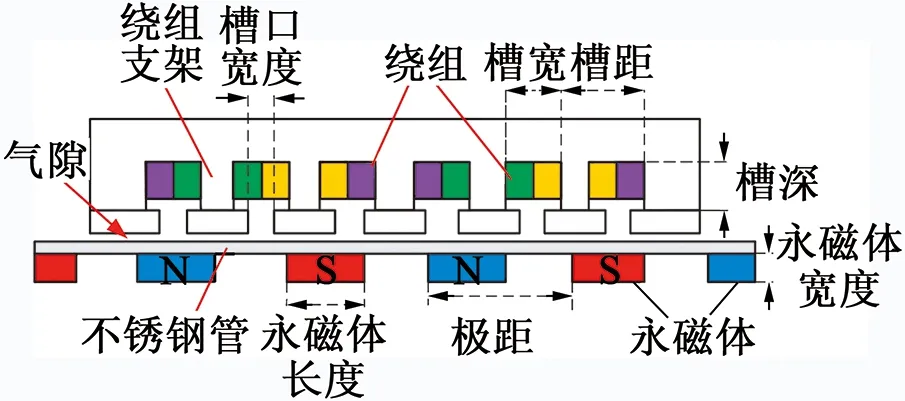
圖2 ITPMLM剖面結構示意圖

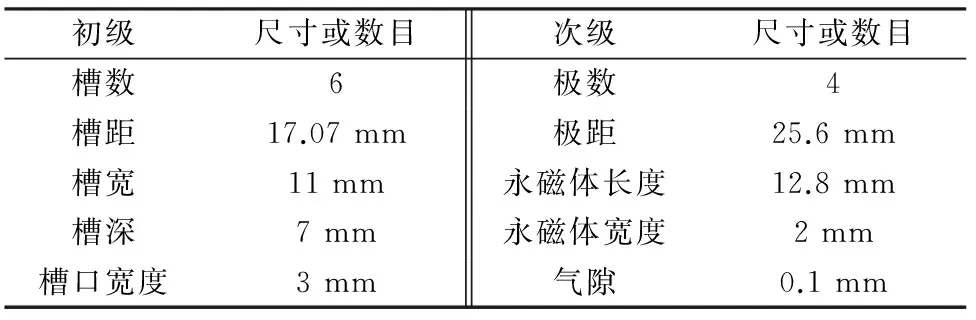
初級尺寸或數目次級尺寸或數目槽數6極數4槽距17.07mm極距25.6mm槽寬11mm永磁體長度12.8mm槽深7mm永磁體寬度2mm槽口寬度3mm氣隙0.1mm

2 滑模變結構控制設計

滑模變結構控制實質是一種綜合的、有效的魯棒控制方法。但該控制方法不同于其它控制方法主要之處在于系統的“結構”是變化的，通過選擇滑模平面，設計控制器，當達到一定匹配要求時，系統依照預設“滑動模態”的狀態軌跡進行運動，對參數攝動和外界干擾具有完全的魯棒性[5-6]，所以變結構控制常被稱為滑動模態控制，簡稱滑模控制。

x(k+1)=Ax(k)+Bu(k)=

(1)

令被控系統的位置指令為r(k)；dr(k)是它的變化率，取R=[r(k);dr(k)]，R1=[r(k+1);dr(k+1)]。用線性外推的方法預測r(k+1),dr(k+1)，即：

(2)

切換函數：

s(k)=Ce[R-x(k)]

(3)

u(k)=(CeB)-1[CeR1-CeAx(k)-s(k+1)]

(4)

趨近律：

s(k+1)=s(k)+T{-εsgn[s(k)]-qs(k)}

(5)

式中：T為采樣周期。由式(4)和式(5)，獲得基于指數趨近律無鐵心圓筒永磁直線電機的離散控制律：

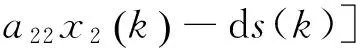
(6)

式中：ds(k)=-εTsgn [s(k)]-qTs(k),且ε>0,q>0。

基于趨近律所設計的離散滑模變結構控制器，可以調節的參數為q，ε，c。其中q為趨近速度參數，q的數值在切換函數動態變化過程起到重要作用，決定了系統趨近滑模面的速度，從而進一步優化被控系統的動態性能。隨著q值的增加，被控系統到達切換平面的速度也隨之加快；當q越趨近于1/T時，被控系統達到切換平面的時間越短[7]。

滑模面參數c決定了控制器切換函數，這是因為c的取值決定了在滑模面上運動的漸進穩定和較好的動態性能[7]。c取值越大，滑模面上的運動速度越快，被控系統的快速性能也就越好。同時，增大滑模參數c和趨近速度參數q的值均可以加快系統響應的快速性。但是過大的參數取值會導致系統輸出量過大，從而使系統出現抖振現象。解決系統參數攝動及外干擾主要靠調節符號函數的增益參數ε，ε取值越大，系統抵抗攝動以及外界干擾的性能就越強。但過大的系統增益會引起系統抖振加大，一般系統的抖振幅度與參數ε成正比關系[7]。

3 實驗平臺搭建

ITPMLM位置控制系統框圖如圖3所示。控制算法采用傳統PID策略和滑模變結構控制方法，從而比較研究在不同的控制策略下，系統的性能差別。系統的參考位置與傳感器反饋的實際位置的差值分別作為兩種控制器的輸入信號，兩控制器的輸出信號分別作用于驅動器進而控制圓筒直線電機。ITPMLM位置控制系統的整體實驗裝置平臺如圖4所示。該位置控制系統主要由無鐵心圓筒永磁直線電機、電源、驅動器、位置傳感器、dSPACE控制板卡和用于編寫控制程序、建立控制界面的計算機等組成。

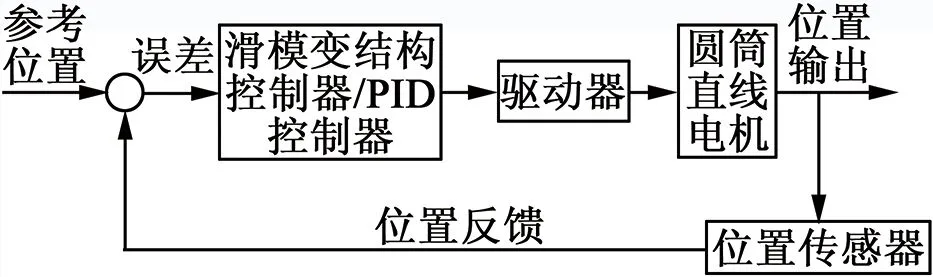
圖3 ITPMLM位置控制系統框圖

4 實驗結果及分析

搭建好實驗平臺，設定系統的輸入信號為頻率為0.5 Hz，幅值為10 mm的方波信號，運行控制程序得到PID控制器以及滑模控制器下ITPMLM的位置跟蹤曲線如圖5所示，圖中顯示PID控制器下ITPMLM在方波的下半周期位置的最低點是-10.38 mm，即ITPMLM在下半周期超調為1.9%。

將圖5中區域A放大得到圖6，可以看出在滑模控制下系統位置響應的上升時間為0.029 s，調節時間為0.026 s(幅值20 mm，±2%的誤差帶)，在上半周期有超調1.35%，PID控制下系統位置響應的上升時間為0.223 s，調節時間為0.123 s。

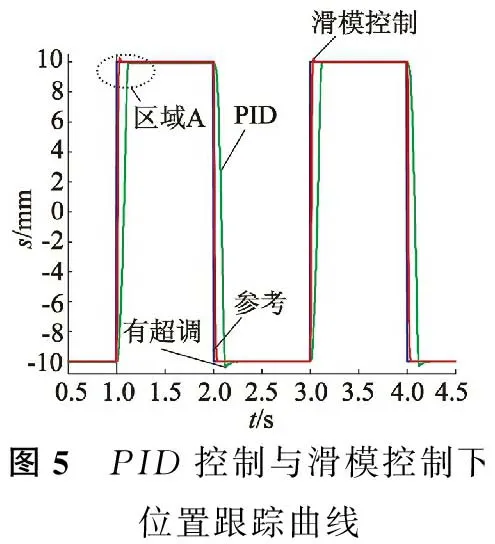
圖5 PID控制與滑模控制下位置跟蹤曲線

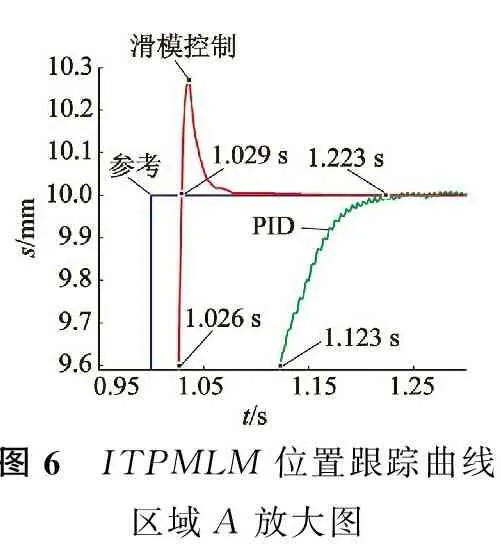
圖6 ITPMLM位置跟蹤曲線區域A放大圖

圖7 為PID控制器與滑模控制器下ITPMLM的位置跟蹤誤差曲線，將區域B放大可以得到圖8，根據圖8可以看出，在PID控制器下系統穩態精度在52 μm內，其中波形上升階段的跟蹤精度為52 μm，下降階段的跟蹤精度為12.5 μm；在滑模控制下系統的穩態精度在3 μm內，其中波形上升階段的跟蹤精度為1 μm，下降階段的跟蹤精度為3 μm。

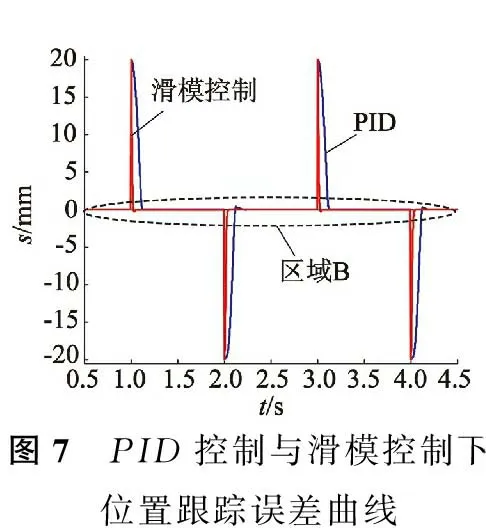
圖7 PID控制與滑模控制下位置跟蹤誤差曲線

圖8 ITPMLM位置跟蹤誤差曲線區域B放大圖

表2匯總了PID控制器與滑模控制器下位置控制系統動態與穩態性能指標。

表2 PID控制與滑模控制下系統響應指標比較

由表2可知，滑模控制較PID控制，系統的響應速度和收斂速度都有所加快，超調減少，系統的穩態精度有了明顯的提升。

5 結 語

本文將一種基于指數趨近律的二階滑模控制方法，應用于對ITPMLM的位置控制，搭建了基于PID控制器與滑模控制器的ITPMLM位置控制系統實驗平臺。實驗結果表明,基于滑模控制器的位置控制系統對ITPMLM的控制取得了快速的暫態性能和良好的穩態性能，其中位置上升時間不超過0.029 s，絕對穩態誤差達到3 μm。

[1] 陳艷龍.圓筒型無鐵心永磁同步直線電機研究[D].南京：東南大學，2014：11-12.

[2] 羅天資，陳衛兵，鄒豪杰,等．直線電機模糊增量PID 控制算法的研究[J].測控技術，2011，30(2):56-59.

[3] 趙曉娟，崔建明．永磁直線同步電動機直接推力控制的仿真研究[J].電氣技術，2012(1):36-39.

[4] 陳展琴,孫宜標,王麗梅,等.基于指數趨近律的永磁直線電機二階滑模控制[C]//第十一屆沈陽科學學術年會暨中國汽車產業集聚區發展與合作論壇論文集(信息科學與工程技術分冊).2014.

[5] 曹廣忠.磁懸浮系統控制算法及實現[M].北京：清華大學出版社,2013:150-154.

[6] 徐世許.不確定系統的終端滑模變結構控制[D].上海：復旦大學，2012:9-10.

[7] 劉金琨,孫富春.滑模變結構控制理論及其算法研究與進展[J].控制理論與應用,2007,24(3):407-418.

Research on Position Control System of Tubular Linear Motor Based on Sliding Mode

XIAJun1，LIQian-long2，PANJian-fei2,ZHANGBo2

(1.Shenzhen Institute of Electronics，Shenzhen 518052,China； 2.Shenzhen Key Laboratory of Electromagnetic Control,Shenzhen 518060,China)

Non-core tubular linear motor has the advantages of light weight, low inertia and fast response, it is widely used in industrial processing and manufacturing fields.Since these control systems were susceptible to parameter variations and load disturbances and other uncertainties, and the traditional proportional-integral-derivative (PID) controllers is hard to guarantee that the controlled objects have a fast and a good steady-state performance, a sliding mode algorithm based on exponential reaching law was adopted to shorten the sliding variables approaching time, and then the response rate of position control system for linear motor was improved.The experiment results show that this method makes the position control system is capable of fast response and good steady-state performance, the rise time is no more than 29 ms and the absolute steady-state error falls into 3 μm in the amplitude of 10mm, a frequency of 0.5 Hz square wave position reference signal.

ironless tubular linear motor; sliding mode; position control; reaching law

2016-03-22

國家自然科學基金項目(51477103,51577121)；廣東省自然科學基金項目(S2014A030313564，S2015A010106017)

TM359.4

A

1004-7018(2016)09-0086-03

夏俊(1971-)，男，碩士，研究方向為電子及通信技術。