天線系統縮比模型參數轉換關系研究

宮 燁，翟 琦，李春騰

(海軍工程大學 電子工程學院，湖北 武漢 430033)

?

天線系統縮比模型參數轉換關系研究

宮 燁，翟 琦，李春騰

(海軍工程大學 電子工程學院，湖北 武漢 430033)

盡管計算機仿真功能強大，但物理模型實驗在天線系統設計中的作用仍不容忽視。由麥克斯韋方程出發，對天線系統建模時縮比模型參數需要滿足的條件進行推導，進而得出天線系統與縮比模型之間相關物理量的轉換關系。以美軍羅羅里和卡特勒甚長波天線為例，利用所推公式對相應物理縮比模型的對應參數進行計算，總結建立縮比模型及實驗的大致流程，為今后天線系統縮比模型的建立起指導作用。

天線系統；縮比模型；參數轉換；麥克斯韋方程

0 引言

盡管如今計算機仿真功能強大，但物理模型實驗的作用仍不容小覷，因為在建立數學模型的過程中，不可避免地要忽略一些因素，計算機仿真就不可能完全取代物理模型實驗。基于相似原理的物理模型實驗方法[1]，具有尺寸小、成本低、便于測試及減少真實設計盲目性、降低研制風險的作用[2]。兩種手段并不相互矛盾而是相互補充,尤其是像結構龐大復雜的(甚)長波天線系統，造價昂貴，更應重視物理模型實驗。

電磁系統模型可分為定性的縮比模型和定量的縮比模型。定性的縮比模型只要求場力線的幾何結構相似,而無需同實際系統的有關參數成特定比例[3]。如果除場力線幾何結構相似外，模型與實際系統的有關參數有特定的比例關系，就成了定量的縮比模型，從理論上講它能得到真實系統幾乎所有電磁特性的定量資料。

1 參數轉換推導

由于麥克斯韋方程的線性關系，在這里必須排除系統的非線性介質(如鐵磁介質)。下面由麥克斯韋方程出發來確定系統縮比模型應滿足的條件。在實際的天線系統中，空間任一點p(x,y,z)的場可采用有理化MKSA單位制以如下方程描述[4]：

(1)

(2)一般電磁場的結構關系并不取決于描述它的坐標系和單位制[5]，因此，在研究模型的場時，可引入新的正交坐標系和單位制而不失其一般性。新的坐標系和單位制與上述坐標系和MKSA單位制有如下關系：

x=mx′ ,y=my′ ,z=mz′ ,t=γ·t′ ,

(3)

E(x,y,z,t)=α·E′(x′,y′,z′,t′),

(4)

H(x,y,z,t)=β·H′(x′,y′,z′,t′),

(5)

ε(x,y,z,t)=Rεε′(x′,y′,z′),

(6)

μ(x,y,z,t)=Rμμ′(x′,y′,z′) ,

(7)

σ(x,y,z,t)=Rσσ′(x′,y′,z′) ,

(8)

此處m、γ、α、β、Rε、Rμ、Rσ為相應物理量的比例因子。

將式(3)～式(8)分別代入式(1)、式(2)得：

(9)

(10)

(11)

(12)

聯立式(1)、式(2)、式(9)～式(12)得：

(13)

(14)

如滿足：

(15)

則式(13)、式(14)可化為與式(1)、式(2)相同的形式：

(16)

(17)

只要兩系統的參數之間滿足式(15)，則兩系統相應點的電磁場就相同[6,7]。

在建立縮比模型并進行實驗時主要考慮兩方面內容[8]：① 模型的空間幾何尺寸、相對位置及電磁場分布等；② 模擬系統與真實系統相關性能參數的轉換。

從式(15)可得出兩系統介質特性參數的轉換關系：

(18)

(19)

(20)

實際天線的場量與真實模型中相應量的轉換關系，可以根據定義由介質的特性參數ε、σ、μ和場矢量E、H來確定。

如：實際天線的玻印廷矢量P定義為：

P=E×H，

(21)

模型中相應的玻印廷矢量為[9]：

(22)

實際天線輻射通過S面的總能量為：

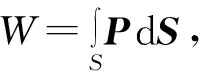
(23)

模型系統相應的量：

(24)

實際天線在空間任意兩點p1,p2之間作用的電壓為：

(25)

式中，dl為沿曲線p1p2的長度矢量元。模型系統中相應量為：

(26)

傳導電流密度：

J=σE，

(27)

(28)

系統中總電流的關系：

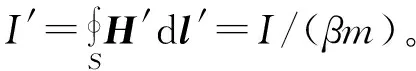
(29)

電阻的關系：

R′=V′/I′=(β/α)R。

(30)

實際天線的增益定義為：

G=(4πr2W)/P，

(31)

式中，W是指定方向上的輻射密度(單位面積上通過的功率)，P是總的輸入功率，模型中的增益：

G′=4π(r′)2W′/P′=G，

(32)

二者增益應相同。

從式(18)、式(19)、式(20)的條件來看，任意選取4個比例因子m、α、β和γ，都可能作出實際天線的縮比模型。但實際上受限于介質參數ε、σ和μ 的范圍，所以上述比例因子并不能任意選擇。譬如在自然界中除鐵磁介質以外的媒質，其導磁率幾乎與自由空間的相同，通常取：

μ′(x′,y′,z′)=μ(x,y,z)=4π×10-7H/m，

(33)

則從式(18)得：

(34)

一般情況下，實際天線與模型都處在空氣中

ε′(x′,y′,z′)=ε(x,y,z)，

(35)

則從式(19)得：

(36)

比較式(34)和式(36)，可以看出兩方程同時成立的條件是：

α/β=1。

(37)

即應有：

α=β；m=γ，

(38)

從式(20)結合上述條件，則有：

σ′(x′,y′,z′)=mσ(x,y,z)，

(39)

t′=t/m。

(40)

因此，對于模型系統，只需選2個比例因子即m、α(或β)即可。α/β是實際天線系統空間阻抗與模型系統空間阻抗之比，由于兩系統處于同一介質中，故系統空間阻抗應相同[10]。式(37)雖然只是限制了α和β的比值，對它們自身的選值并無限制，但一般情況下，實際系統與模型系統都采用相同的單位制，通常選α=β=1。

在滿足式(38)～式(40)的條件下，如能保證模型的輸入功率等于實際天線輸入功率的1/(αβm2)倍，該模型系統就成為定量的縮比模型[10]，但由于實現起來有一定困難，所以往往只能得到大部分物理量的數值結果。

一個定量的縮比模型應滿足的條件是：

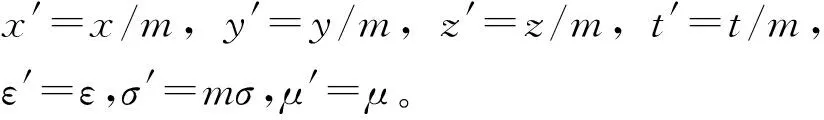
(41)

上式表明模型與實際天線系統相比在空間和時間上都要縮小m倍，介質電導率要增大m倍。m是任意的，但必須考慮實際環境只允許模型有適當的尺寸。定量的縮比模型能夠直接得到的物理量與實際天線相應量的轉換關系如表1所示[3]。此外，縮比模型還可以確定極化方向、頻帶寬度和方向圖等不依賴于能量的那些量。

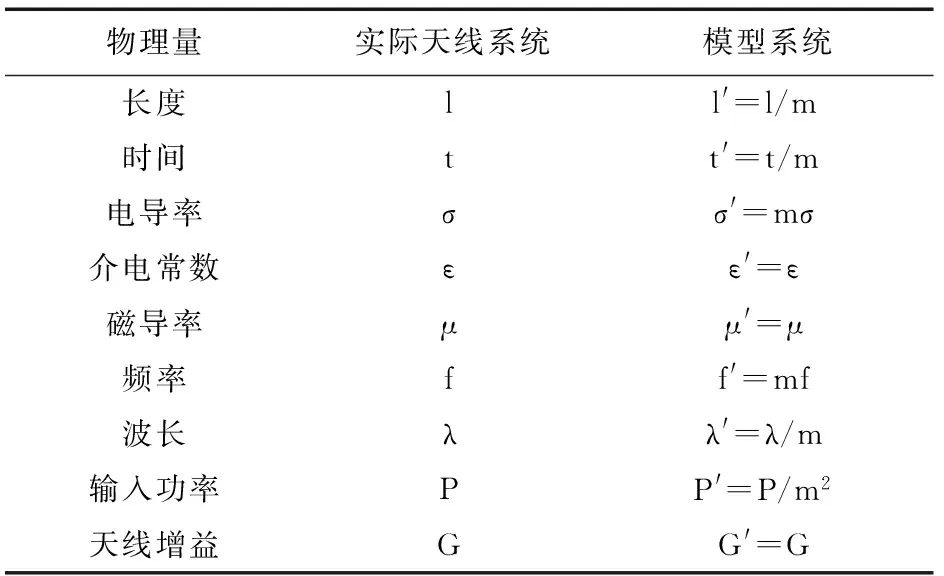
表1 參數轉換關系

2 天線實例計算

下面以美軍位于夏威夷的羅羅里甚長波發信臺和緬因州的卡特勒臺為例，利用上文推導所得參數轉換關系，計算在建立定量的縮比模型時的相應參數。

羅羅里甚長波發信天線由7座高h=183 m的鐵塔和3座支撐塔組成以及天線電纜組成，鐵塔間橫向距離a=381 m，縱向距離b=304.8 m，為帶一角形頂負載的矩形天線陣，發射機輸出功率為1 000 kW,工作頻率范圍為10～20 kHz。

根據1英尺=0.304 8 m將實際天線尺寸進行換算，得鐵塔高度為h=183 m。取縮比因子m=200，得模型鐵塔高為h′=0.92 m，鐵塔間橫向距離為a′=1.91 m，縱向距離為b′=1.52 m。另根據頻率以及發射功率的轉換關系得該定量縮比模型的工作頻率范圍應為2～4 MHz，發射機輸出功率為25 W。表2為羅羅里天線系統實際參數以及取縮比因子m=200后所得模型的具體參數。

表2 羅羅里天線實參及模型參數

緬因州的卡特勒天線是目前輻射效率最高的甚長波天線，該天線由兩組六角星形天線陣組成，共有26座鐵塔，其中心塔高h0=298 m，內圈塔高h1=266 m，外圈塔高h2=243 m，內半徑r1=558 m，外半徑r2=935 m。

其單組天線結構示意圖如圖1所示。發射機輸出功率為2 000 kW，工作頻率范圍為14～30 kHz。

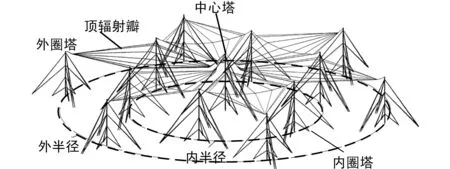
圖1 卡特勒單組天線示意圖

取縮比因子m=200，得模型中心塔高為h0′=1.49 m，內圈塔高為h1′=1.33 m，外圈塔高為h2′=1.22 m。內半徑為r1′=2.79 m，外半徑為r2′=4.68 m。發射機輸出功率為50 W，對應的工作頻率為2.8～6 MHz。表3為卡特勒天線實際參數以及取縮比因子m=200后所得模型的具體參數。

表3 卡特勒天線實參及模型參數

通過對以上美軍羅羅里和卡特勒甚低頻發信天線進行實例計算，得到今后為天線系統建立縮比模型以及進行物理模型實驗的大致流程。首先，根據天線尺寸確定合適的縮比因子m,將天線按比例進行縮小；其次，將實際天線系統的工作頻率以及發射機功率等參數按照所推導的參數轉換關系進行換算；最后，對模型天線的相關參數進行測量，進而可大致反映出實際天線系統的有關性能。但由于σ′=mσ這一條件很難實現，因此對模型阻抗進行測量時將存在一定誤差。

3 結束語

由麥克斯韋方程出發，對建立天線系統縮比模型時需滿足的條件，以及相應參數的轉換關系進行了推導，并結合美軍甚長波臺實際參數對縮比模型對應參數進行計算，為今后天線系統縮比模型的建立有指導作用。但也應認識到對于σ'=mσ這一條件，在實現時較難做到，故在模型上測量損耗電阻時將存在一定誤差。

[1] 齊萬泉,汪宗福,馬蔚宇,等.相似原理應用于混響室縮比模型的驗證分析[J].電波科學學報,2011,26(1):180-185.

[2] 周利霖,唐國金.大型飛艇縮比模型設計方法研究[C]∥第三屆高分辨率對地觀測學術年會優秀論文集,2014,12:79-83.

[3] 王 冰.甚低頻天線縮比模型研究[J].黑龍江科技信息,2012(6)：58-61,131.

[4] 盧萬錚.天線理論與技術[M].西安：西安電子科技大學出版社,2004.

[5] 陳抗生.電磁場與電磁波[M].北京：高等教育出版社，2003.

[6] 趙 輝.預警機雷達天線輻射特性的縮比模型測試法[J].微波學報,2014(3)：308-311.

[7] 陸 軍,趙 輝.縮比模型法測試載機對雷達天線方向圖影響[C]∥2011年全國微波毫米波會議論文集(下冊),2011,06:151-156.

[8] 鄭 星,汪連棟.縮比模型實驗技術在射頻仿真暗室設計中的應用[J].電視技術,2008,48(5):32-35.

[9] 湯仕平,陳黎平,萬海軍,等.電磁兼容性船模預測在電波暗室內的實現[J].中國造船,2006,47(2):42-48.

[10]梁高權.甚低頻波和超低頻波的輻射與傳播[M].武漢:海軍工程大學出版社,2002.

Research on Parameters Conversion Relation between Antenna System and Its Reduced-scale Model

GONG Ye，ZHAI Qi，LI Chun-teng

(College of Electronic Engineering,Naval University of Engineering,Wuhan Hubei 430033,China)

Though the function of computer simulation is powerful,the role of physical model experiment in the antenna system design allows of no ignorance.Based on the Maxwell equations,conditions to be fulfilled when the antenna system reduced-scale model is established are derived,and thus the related physical quantities conversion relation between the antenna system and the reduced-scale model are obtained.Taking the American Laulaulei and Culter VLF antenna as example,the derived formula is used to calculate the corresponding parameters of the corresponding model,and the process for establishing the reduced-scale model and making experiment is summarized.The researchcan provide guidance for future establishment of antenna system reduced-scale model.

antenna system;reduced-scale model;parameters conversion;Maxwell equations

10.3969/j.issn.1003-3114.2016.06.18

宮 燁，翟 琦，李春騰.天線系統縮比模型參數轉換關系研究[J].無線電通信技術,2016,42(6):70-72,94.

2016-07-15

宮 燁(1991—)，男，碩士研究生，主要研究方向：長波天線相關技術。翟 琦(1977—)，男，講師，碩士研究生，主要研究方向：天線理論與技術。

TN911.22

A

1003-3114(2016)06-70-3