基于支持向量回歸機的顆粒阻尼減振結(jié)構(gòu)阻尼特性實驗
夏兆旺, 魏守貝, 張 帆, 王雪濤, 陳志超, 候 星
(1. 江蘇科技大學(xué) a. 能源與動力工程學(xué)院;b. 船舶與海洋工程學(xué)院,江蘇 鎮(zhèn)江 212003;2. 中國運載火箭技術(shù)研究院 研究發(fā)展中心,北京 100076)
?
基于支持向量回歸機的顆粒阻尼減振結(jié)構(gòu)阻尼特性實驗
夏兆旺1a, 魏守貝1a, 張 帆2, 王雪濤1a, 陳志超1a, 候 星1b
(1. 江蘇科技大學(xué) a. 能源與動力工程學(xué)院;b. 船舶與海洋工程學(xué)院,江蘇 鎮(zhèn)江 212003;2. 中國運載火箭技術(shù)研究院 研究發(fā)展中心,北京 100076)

將基于遺傳算法(GA)的支持向量回歸機(SVR)用于建立顆粒阻尼減振結(jié)構(gòu)阻尼特性預(yù)測模型。應(yīng)用基于結(jié)構(gòu)風(fēng)險最小化準(zhǔn)則的SVR,建立顆粒阻尼減振結(jié)構(gòu)阻尼特性—影響因素SVR預(yù)測模型,對顆粒阻尼減振結(jié)構(gòu)的阻尼特性進行預(yù)測,并通過實驗進行了驗證。結(jié)果表明:在選擇適當(dāng)?shù)膮?shù)和核函數(shù)的基礎(chǔ)上,利用該方法建立的預(yù)測模型,平均相對誤差在10.3%左右;顆粒阻尼器的減振性能隨填充率的增加而增加,顆粒填充率75%時,減振性能最好;顆粒密度是影響顆粒阻尼器減振效果的重要因素,顆粒密度越大系統(tǒng)的減振性能越好;顆粒阻尼器的減振性能隨著顆粒直徑的變化不明顯。
阻尼比; 遺傳算法; 支持向量回歸機
0 引 言
相比其他阻尼材料,如黏彈性阻尼材料,顆粒阻尼擁有更好減振性和魯棒性[1-3]。顆粒阻尼減振結(jié)構(gòu)的阻尼特性隨顆粒、結(jié)構(gòu)及阻尼器參數(shù)呈明顯非線性變化特性[4-7]。顆粒、結(jié)構(gòu)和阻尼器參數(shù)對顆粒阻尼結(jié)構(gòu)減振效果的影響規(guī)律是目前國內(nèi)外學(xué)者主要關(guān)注的研究方向[8-9]。目前,對顆粒阻尼減振特性的研究主要以實驗為主[10],雖然采用實驗方法可測定到相對準(zhǔn)確的阻尼特性,但對于處理小樣本、高維度、非線性影響因素指標(biāo)的數(shù)據(jù)時,復(fù)雜的測量過程相當(dāng)耗時[11-14]。近年來,提出的基于結(jié)構(gòu)風(fēng)險最小化理論的支持向量機方法[15-16]克服了人工神經(jīng)網(wǎng)絡(luò)等方法的缺點,是目前針對小樣本分類、回歸等最常采用的方法。
本文采用支持向量回歸機(SVR)建立顆粒阻尼減振結(jié)構(gòu)阻尼特性—影響因素模型,利用建立的模型對顆粒阻尼減振結(jié)構(gòu)的阻尼特性進行預(yù)測,并進行了實驗驗證,進一步推動顆粒阻尼減振技術(shù)的工程應(yīng)用。
1 SVR的基本原理
1.1 SVR
對于引入線性ε-SVR,給定若干個獨立同分布的學(xué)習(xí)樣本(xi,yi),i=1,2,…,n,其中xi∈Rn,yi∈R。線性回歸的問題是在給定訓(xùn)練點后,能夠?qū)ふ业脚c訓(xùn)練點偏差較小的直線y=f(x)=ωx+b。即在
(1)
條件下,轉(zhuǎn)化為求解優(yōu)化目標(biāo)函數(shù)的最小化問題:
(2)
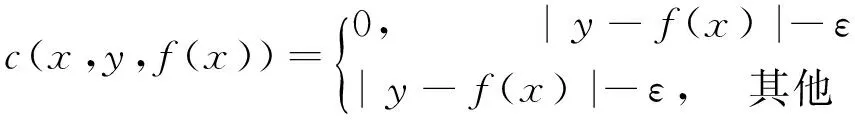
(3)
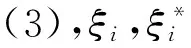
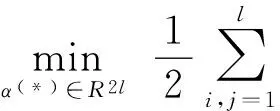
(4)
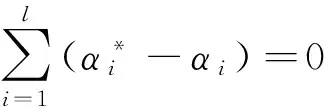
(5)

非線性支持向量回歸和線性回歸過程類似,不同的是如何處理輸入向量。非線性回歸首先通過非線性映射將輸入向量映射到一個高維特征空間(Hilbert空間)中,
Φ:Rn→Η,x→Φ(x)
然后在此高維空間中再進行線性回歸,此時涉及到高維特征空間點積運算:
k(xi,xj)=Φ(xi)·Φ(xj)
非線性回歸求解的核心是如何選取核函數(shù)。核函數(shù)選擇合適就可以得到非線性回歸的擬合函數(shù):
(5)

1.2 基于GA優(yōu)化SVR參數(shù)
通過對SVR最優(yōu)參數(shù)的研究發(fā)現(xiàn)[7],懲罰系數(shù)C和核函數(shù)參數(shù)γ對結(jié)果影響明顯,所以如何優(yōu)化SVR參數(shù)很重要。
遺傳算法[8]可用于優(yōu)化SVR參數(shù),其主要步驟如下:① 確定懲罰系數(shù)和核函數(shù)參數(shù)的可能取值范圍;② 隨機選擇參數(shù)的初始值,采用編碼的方法構(gòu)造初始種群;③ 將構(gòu)造種群的個體輸入到SVR模型進行訓(xùn)練,計算適用度函數(shù)值;④ 判斷適用度函數(shù)值是否滿足要求或達到最大遺傳代數(shù)。如果滿足,直接輸出SVR最佳參數(shù),并通過對訓(xùn)練樣本的訓(xùn)練得到訓(xùn)練模型;反之,則應(yīng)用選擇、交叉以及變異算子產(chǎn)生新的種群再次進行迭代運算。
2 顆粒阻尼減振結(jié)構(gòu)阻尼特性預(yù)測
2.1 影響顆粒阻尼減振結(jié)構(gòu)阻尼特性因素
對顆粒阻尼懸臂梁結(jié)構(gòu)的阻尼特性進行實驗,在懸臂梁自由端固定一個可填充顆粒的金屬盒,利用加速度傳感器測試懸臂梁相應(yīng)位置的加速度響應(yīng),實驗測試系統(tǒng)如圖1所示。懸臂梁實驗件的材料為鑄鋼,材料密度7.8×103kg/m3, 彈性模量E=175 GPa;懸臂梁結(jié)構(gòu)尺寸如下:長300 mm 、寬25 mm、厚 4 mm;用以填充顆粒的金屬盒質(zhì)量122 g;測試懸臂梁振動加速度傳感器采用YD-39型,質(zhì)量16 g。
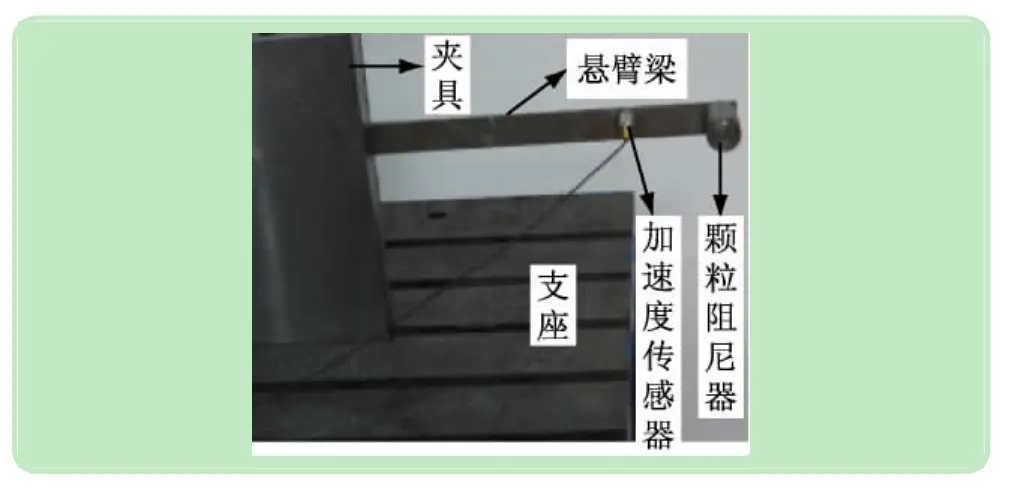
圖1 顆粒阻尼懸臂梁實驗測試系統(tǒng)
經(jīng)過研究發(fā)現(xiàn),顆粒阻尼減振結(jié)構(gòu)的減振特性受到顆粒尺寸、顆粒密度、填充率、腔體的外形和尺寸、結(jié)構(gòu)振動的頻率和幅值、阻尼器位置等因素的影響[9-10]。通過大量的實驗數(shù)據(jù)可以看出,這些影響因素對顆粒阻尼減振結(jié)構(gòu)的阻尼特性的影響程度不同,但它們之間又存在著某種多元強非線性的映射關(guān)系。如何準(zhǔn)確建立含多元參數(shù)的強非線性顆粒阻尼減振結(jié)構(gòu)阻尼特性預(yù)測模型具有重要意義。
2.2 阻尼特性預(yù)測模型
為了定量地研究顆粒阻尼減振結(jié)構(gòu)的阻尼特性,需建立一個數(shù)學(xué)模型來反映顆粒阻尼減振結(jié)構(gòu)阻尼特性和各種影響因素之間的映射關(guān)系,其數(shù)學(xué)模型表達式如下:
Y=F(X)=F(A,B,C,D,E,F,G,H…)
其中:Y為顆粒阻尼減振結(jié)構(gòu)的阻尼比;A為顆粒尺寸;B為顆粒密度;C為填充率;D為腔體外形;E為腔體尺寸;F為減振結(jié)構(gòu)的振動頻率;G為減振結(jié)構(gòu)的振動幅值;H為阻尼器位置。將Xi=(x1,x2,x3,x4,x5,x6,x7,x8…)作為支持向量機的輸入向量,Yi作為其輸出變量,組成(Xi,Yi)的訓(xùn)練對。利用這些數(shù)據(jù)可訓(xùn)練建立預(yù)測模型,模型結(jié)構(gòu)如圖2所示,訓(xùn)練模型的準(zhǔn)確性可通過訓(xùn)練集進行驗證,其結(jié)果如圖3所示。
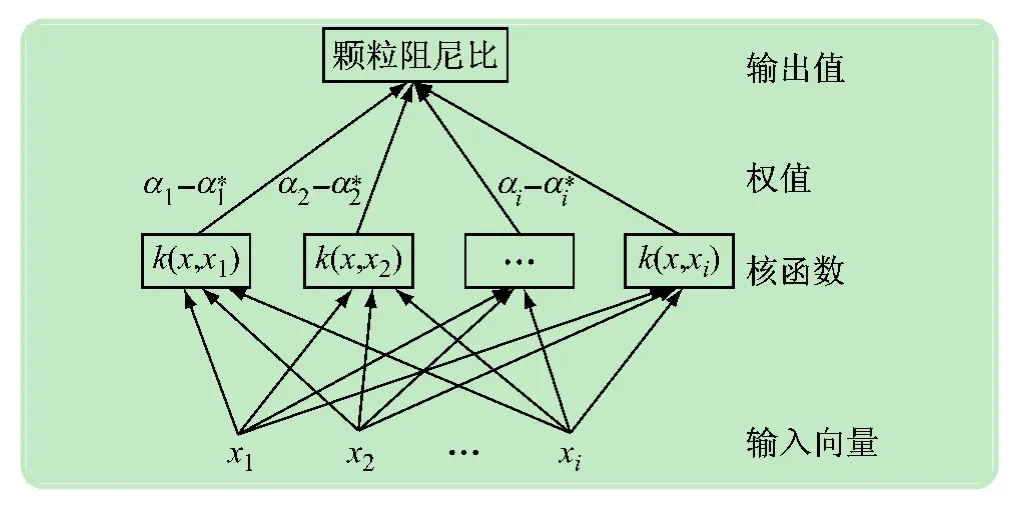
圖2 顆粒阻尼結(jié)構(gòu)阻尼特性預(yù)測模型

圖3 顆粒阻尼結(jié)構(gòu)訓(xùn)練模型
3 帶顆粒阻尼懸臂梁結(jié)構(gòu)阻尼特性預(yù)測分析
3.1 特征向量的提取
為了驗證本文方法的有效性,選取帶顆粒阻尼器的懸臂梁結(jié)構(gòu)阻尼特性的90個實驗數(shù)據(jù)作為算例[10],帶顆粒阻尼的懸臂梁結(jié)構(gòu)阻尼特性的影響因素考慮:A;B(本文材料均為鋼球,用1表示);C;G;H(距固定端的距離)。Xi=(A,B,C,G,H)就可以組成輸入特征向量,通過時域衰減法測得對應(yīng)工況下的帶顆粒阻尼的懸臂梁結(jié)構(gòu)的阻尼比yi作為輸出值,即yi=f(xi)=ω·φ(xi)+b。
3.2 實驗數(shù)據(jù)預(yù)處理
為了準(zhǔn)確選擇SVR中各參數(shù)和減少計算復(fù)雜度,對原始數(shù)據(jù)(因變量、自變量)進行歸一化預(yù)處理( 本文歸一化到[-1,1]區(qū)間)。
3.3 核函數(shù)的選擇
目前對于核函數(shù)的選擇,學(xué)術(shù)界暫無統(tǒng)一標(biāo)準(zhǔn)。本文選擇常用的高斯徑向基核函數(shù),
3.4 阻尼特性預(yù)測模型
將實驗數(shù)據(jù)工況號為1,3,5,…,89的45個樣本作為訓(xùn)練樣本,工況號2,4,6,…,90的45個的樣本作為測試樣本,每一個工況號對應(yīng)一組實驗工況(初始振幅G,填充率C,直徑A,材料B,距固定端的距離H),參數(shù)尋優(yōu)算法、偶數(shù)工況號預(yù)取值(為保證SVR預(yù)測結(jié)構(gòu)的完整性)及預(yù)測結(jié)果如表1所示(保留4位有效數(shù)字)。其中:a為誤差小于20%的樣本個數(shù);b為誤差20%~30%的樣本個數(shù);c為誤差30%~40%的樣本個數(shù);d為誤差40%~50%的樣本個數(shù);e為誤差50%~60%的樣本個數(shù);f為誤差60%~70%的樣本個數(shù);g為誤差70%~80%的樣本個數(shù);h為誤差80%~90%的樣本個數(shù);i為誤差90%~100%的樣本個數(shù);j為誤差大于100%的樣本個數(shù)。
采用不同SVR參數(shù)尋優(yōu)方法訓(xùn)練回歸模型的準(zhǔn)確率:交叉驗證法(CV)93.16%;遺傳算法(GA)93.65%;粒子群優(yōu)化(PSO)95.20%。可以看出,采用CV、GA、PSO 3種常用的SVR參數(shù)尋優(yōu)方法訓(xùn)練回歸模型的準(zhǔn)確率大體相同,采用CV、GA優(yōu)化參數(shù)的模型的準(zhǔn)確率比PSO相對低些,就參數(shù)尋優(yōu)單方面來看,3種算法都可以對顆粒阻尼減振結(jié)構(gòu)阻尼特性的預(yù)測模型進行參數(shù)優(yōu)化,準(zhǔn)確度高。
不同參數(shù)尋優(yōu)算法下偶數(shù)工況號取值對顆粒阻尼減振結(jié)構(gòu)阻尼特性預(yù)測結(jié)果的影響如表1~3所示。研究發(fā)現(xiàn),相同參數(shù)尋優(yōu)算法下,偶數(shù)工況號取平均值、均方根值、前一工況號值對顆粒阻尼減振結(jié)構(gòu)阻尼特性的預(yù)測結(jié)果幾乎沒有影響。在偶數(shù)工況號取值一致的情況下,CV和GA法的預(yù)測精度比PSO的預(yù)測精度要高。通過對比,本文采用GA優(yōu)化SVR參數(shù),偶數(shù)工況號取前一工況號值的組合方式進行預(yù)測實驗。
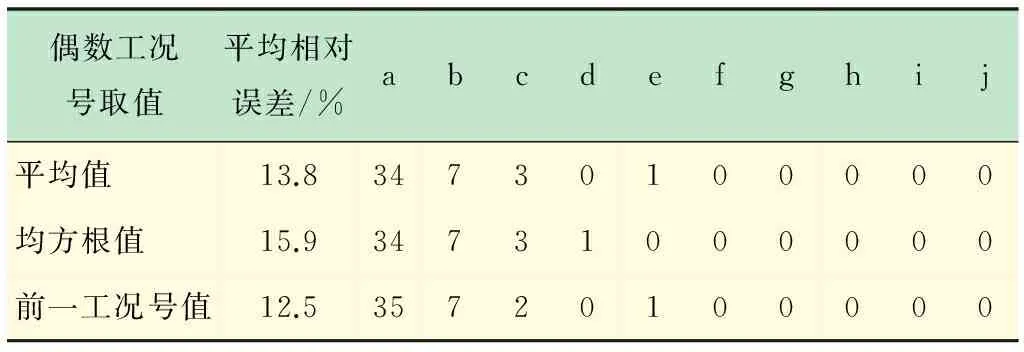
表1 CV優(yōu)化參數(shù)、偶數(shù)工況號取值對應(yīng)的誤差結(jié)果
針對上述顆粒阻尼減振結(jié)構(gòu)阻尼特性—影響因素GA-SVR預(yù)測模型,在Matlab 7.12環(huán)境下進行訓(xùn)練與測試的仿真實驗,并通過GA得到SVR參數(shù)C=1.231 7,γ=0.304 22。采用GA優(yōu)化參數(shù)偶數(shù)工況號取前一工況號值的方式,得到測試樣本的仿真結(jié)果如表4和圖4所示。可以看出,除一小部分工況號數(shù)據(jù)預(yù)測不準(zhǔn)確(分析認(rèn)為導(dǎo)致如工況號6、8、13、28、40點出現(xiàn)較大偏差的原因歸結(jié)為原始數(shù)據(jù)測量不夠精確)外,總體上看,顆粒阻尼減振結(jié)構(gòu)阻尼特性的預(yù)測結(jié)果能滿足預(yù)測要求,誤差小,擬合程度較高。

表2 GA優(yōu)化參數(shù)、偶數(shù)工況號取值對應(yīng)的誤差結(jié)果
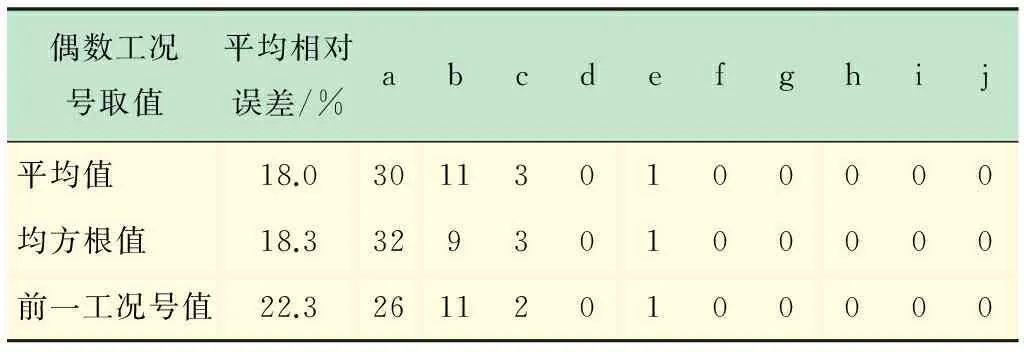
表3 PSO優(yōu)化參數(shù)、偶數(shù)工況號取值對應(yīng)的誤差結(jié)果

圖4 SVR預(yù)測結(jié)果
3.5 阻尼特性預(yù)測分析
基于上述建立的模型,對懸臂梁顆粒阻尼系統(tǒng)的阻尼特性與顆粒直徑、顆粒密度及填充率等參數(shù)之間關(guān)系進行了分析,結(jié)果如圖5~7所示。
從圖5可以看出:顆粒阻尼器的減振性能隨著顆粒直徑的變化不明顯,在同等環(huán)境下,對于阻尼比的影響不如填充率和顆粒密度。
從圖6可以看出:顆粒阻尼器的減振性能隨填充率的增加而增加,在顆粒填充率達到75%時,減振性能增加明顯,填充率達到80%時,減振性能區(qū)域穩(wěn)定。原因是在填充率較小時,顆粒之間的間隙較大,顆粒之間的相互碰撞和摩擦不夠;當(dāng)填充率達到80%時,顆粒阻尼器內(nèi)顆粒過于密集,顆粒的運動受限制,顆粒阻尼器的減振性能增加有限。
從圖7可見:顆粒密度是影響顆粒阻尼器減振效果的重要因素,顆粒密度越大,系統(tǒng)的減振性能越好。
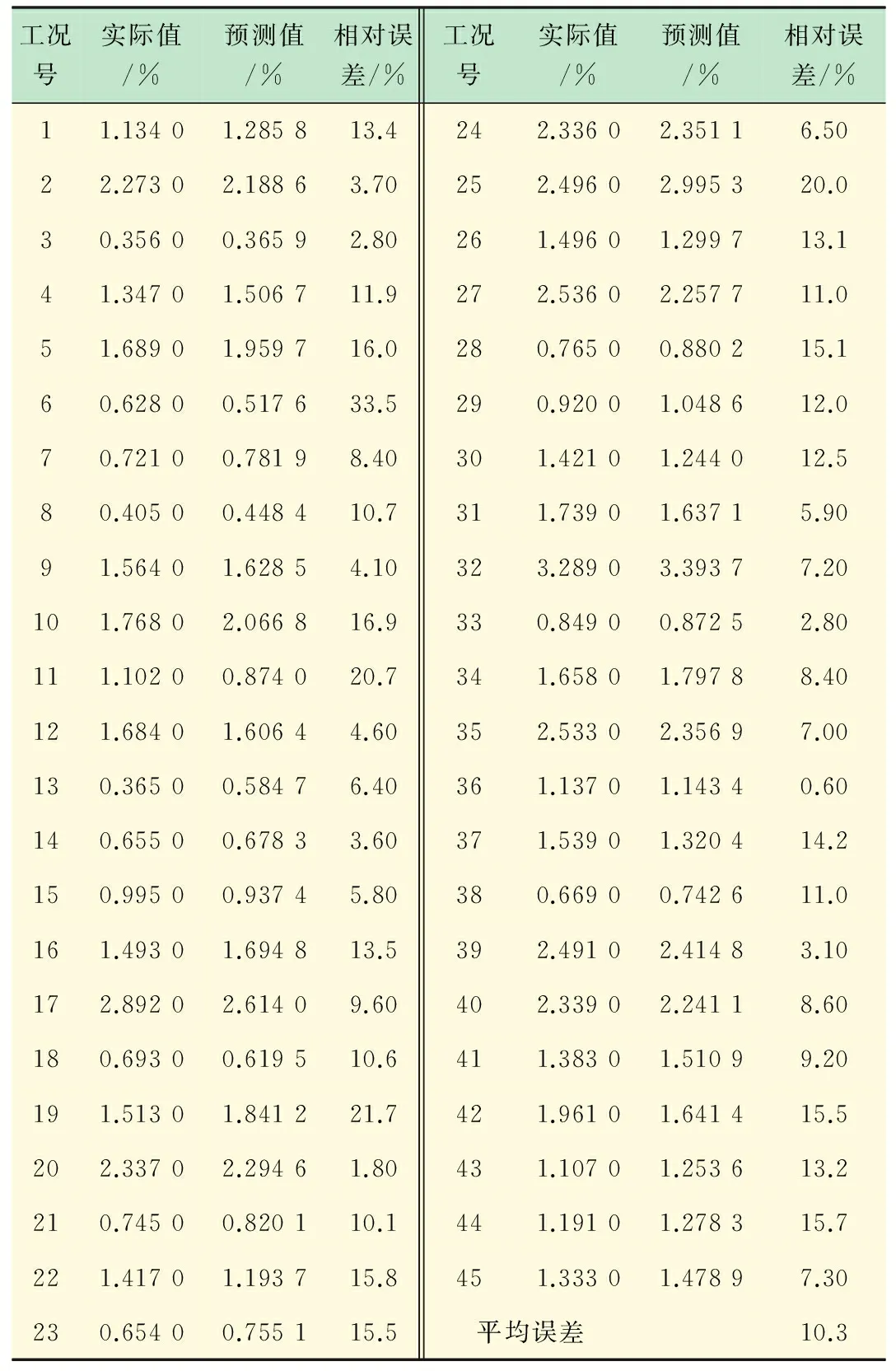
表5 顆粒阻尼減振結(jié)構(gòu)阻尼比預(yù)測結(jié)果(GA優(yōu)化參數(shù)、偶數(shù)工況號取前一工況號值)
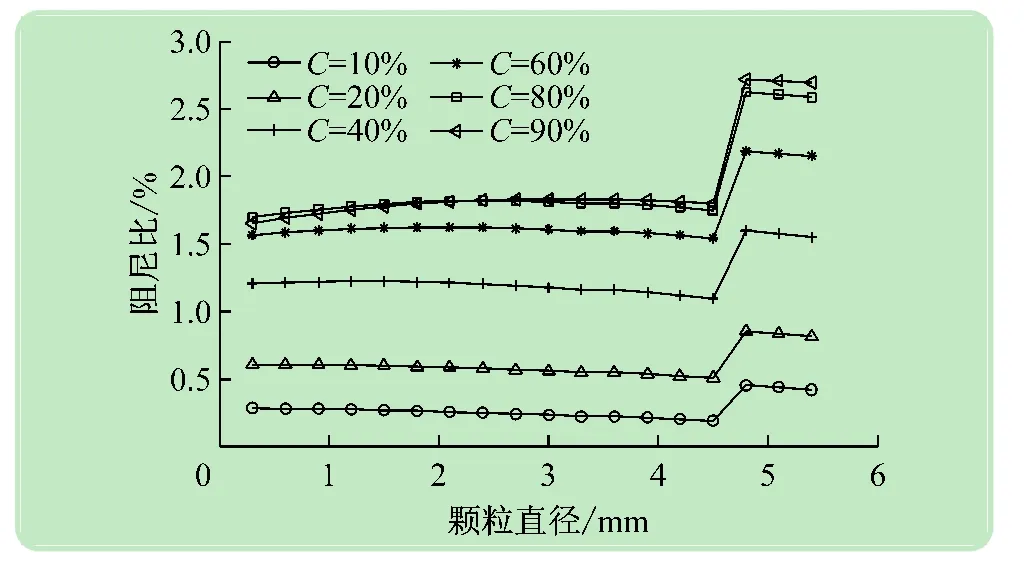
圖5 阻尼比隨著顆粒直徑的變化曲線

圖6 阻尼比隨著填充率的變化曲線

圖7 阻尼比隨著顆粒密度的變化曲線
4 結(jié) 語
本文將GA-SVR方法應(yīng)用于顆粒阻尼減振結(jié)構(gòu)阻尼特性的預(yù)測,提出了基于GA的SVR參數(shù)優(yōu)化方法,實驗證明,GA能夠選取較優(yōu)的SVR參數(shù)。建立了顆粒阻尼減振結(jié)構(gòu)阻尼特性—影響因素的預(yù)測模型,通過模型得到的預(yù)測值和實際值具有較高的一致性,平均相對誤差在10.3%左右。
[1] PANOSSIAN H V. Structural damping enhancement via non-obstructive particle damping technique[J]. Journal of Vibration and Acoustics, 1992, 114:101-105.
[2] Yao B, Chen Q, Xiang H Y. Experimental and theoretical investigation on dynamic properties of tuned particle damper[J]. International Journal of Mechanical Sciences, 2014, 80:122-1.
[3] Mohamed Gharib, Saud Ghani. Free vibration analysis of linear particle chain impact damper[J]. Journal of Sound and Vibration, 2013, 332:6254-6264.
[4] Xia Zhaowang, Liu Xiandong, Shan Yingchun. Coupling simulation algorithm of a rotating flat-plate blade with particle dampers under centrifugal forces[J]. Journal of Vibration and Acoustics, Transactions of the ASME, 2011, 133(4):34-41.
[5] Cheng C H, Shiu H Y. A novel GA-SVR time series model based on selected indicators method for forecasting stock price[C]//2014 International Conference on Information Science, Electronics and Electrical Engineering (ISEEE). IEEE, 2014: 395-399.
[6] Wei G, Yu X, Long X. Novel approach for identifying Z-axis drift of RLG based on GA-SVR model[J]. Journal of Systems Engineering and Electronics, 2014, 25(1): 115-121.
[7] 唐和生,薛松濤,陳榮等. 序貫最小二乘支持向量機的結(jié)構(gòu)系統(tǒng)辨識[J]. 振動工程學(xué)報,2006,19(3): 382-387.
[8] 陳 果. 基于一類支持向量機與主成分分析的轉(zhuǎn)靜碰摩故障檢測技術(shù)[J].振動與沖擊, 2012,31(22):29-33.
[9] Xia Zhaowang, Liu Xiandong, Shan Yingchun. Coupling simulation algorithm of discrete element method and finite element method for particle damper[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2009, 28(3):197-204.
[10] Huang Xiuchang, Jiang Aihua, Zhang Zhiyi. Design and optimization of periodic structure mechanical filter in suppression of foundation resonances[J]. Journal of Sound and Vibration, 2011, 330(20): 4689-4712.
[11] Kalteh A M. Wavelet genetic algorithm-support vector regression for monthly flow forecasting[J]. Water Resources Management, 2014,29(4): 1-11.
[12] Guilhem M, AhmadAl, Gwena A. Soft hollow particle damping identification in honeycomb structures[J]. Journal of Sound and Vibration, 2013, 332:536-544.
[13] 杜妍辰, 王樹林. 兩顆粒彈塑性正碰撞的耗散模型[J].機械工程學(xué)報,2009,45(2):149-156.
[14] Zheng Lu, Xilin Lu, Masri S F. Studies of the performance of particle dampers under dynamic loads [J]. Journal of Sound and Vibration, 2010,329:5415-5433.
[15] Vapnik V N. Statistical learning theory [M]. Newyork:Wiley, 1998.
[16] VONG Chiman, WONG Pakkin, TAM Lapmou. Ignition pattern analysis for automotive engine trouble diagnosis using wavelet packet transform and support vector machines[J]. Chinese Journal of Mechanical Engineering, 2011,47(5):870-878.
Prediction of Particle Damping Ratio Based on GA-SVR
XIAZhao-wang1a,WEIShou-bei1a,ZHANGFan2,WANGXue-tao1a,CHENZhi-chao1a,HOUXing1b
(1a. School of Energy and Power Engineering; 1b. School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China; 2. Research and Development Center of China Academy of Launch Vehicle Technology, Beijing 100076, China)
In order to research the effective prediction method of particle damping ratio, genetic algorithm-support vector regression machine(GA-SVR) is used to establish model to predict particle damping ratio. On the basis of GA, we optimize the SVR parameters, apply the support vector regression machine which is based on structural risk minimization criterion to establish the “particle damping ratio-influence factors of the SVR forecasting model”, and then predict particle damping ratio. Experiment analysis shows that on the basis of selecting the appropriate parameters and kernel function, the particle damping ratio prediction model is established and works well. Based on this method, the average relative error is about 10.3%.
damping ratio; genetic algorithm(GA); support vector regression machine(SVR)
2015-04-13
國家自然科學(xué)基金項目(11302088);江蘇省自然科學(xué)基金青年基金(BK2012278)資助項目
夏兆旺(1981-),男,安徽鳳陽人,副教授,現(xiàn)主要從事振動噪聲與控制研究。Tel.:0511-84401147;E-mail:dlxzw@163.com
O 328;TB 34
A
1006-7167(2016)02-0017-05

