與Gamma函數(shù)有關(guān)的對(duì)數(shù)完全單調(diào)函數(shù)及其應(yīng)用

孫梅

（西北大學(xué)數(shù)學(xué)學(xué)院，陜西西安710127）

與Gamma函數(shù)有關(guān)的對(duì)數(shù)完全單調(diào)函數(shù)及其應(yīng)用

孫梅

（西北大學(xué)數(shù)學(xué)學(xué)院，陜西西安710127）

為了完善函數(shù)Gα，β（x）（其中參數(shù)α∈R，β≥0）及函數(shù)1/Gα，β（x）在區(qū)間（0，∞）上的對(duì)數(shù)完全單調(diào)性和相關(guān)不等式，利用Taylor展開(kāi)式、Gamma函數(shù)、Psi函數(shù)的級(jí)數(shù)表達(dá)式和積分表達(dá)式研究了函數(shù)Gα，β（x）和函數(shù)1/Gα，β（x）數(shù)的對(duì)數(shù)完全單調(diào)性，將函數(shù)Gα，β（x）和函數(shù)1/Gα，β（x）對(duì)數(shù)完全單調(diào)的充分條件擴(kuò)大；利用對(duì)數(shù)完全單調(diào)性得到新的不等式，并通過(guò)對(duì)特殊情形的研究，得到一個(gè)形式簡(jiǎn)單對(duì)稱(chēng)的雙邊不等式，該不等式對(duì)階乘數(shù)之乘積與的商做出估計(jì).

Gamma函數(shù)；對(duì)數(shù)完全單調(diào)函數(shù)；充分條件；不等式

1 引言

歐拉Gamma函數(shù)自誕生以來(lái)，作為一類(lèi)特殊函數(shù)，已經(jīng)被很多數(shù)學(xué)家如Gauss、Legendre、Weierstrass、Joseph Liouville關(guān)注和研究.到目前為止，Gamma函數(shù)、Psi函數(shù)、Polygamma函數(shù)［1］理論已經(jīng)日趨成熟，在應(yīng)用方面也達(dá)到一個(gè)新高度.它在概率論、統(tǒng)計(jì)學(xué)、不等式等數(shù)學(xué)分支都有著非常廣泛的應(yīng)用，與Gamma函數(shù)有關(guān)的完全單調(diào)函數(shù)在很大程度上推動(dòng)了不等式理論的發(fā)展.以下介紹完全單調(diào)性和對(duì)數(shù)完全單調(diào)性的概念.

函數(shù)f被稱(chēng)作是區(qū)間I上的完全單調(diào)函數(shù)，如果f在區(qū)間I上的各階導(dǎo)數(shù)都存在，且滿(mǎn)足對(duì)任意的x∈I且n≥0，有

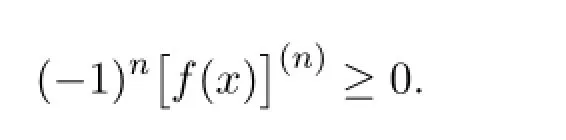
如果此不等式嚴(yán)格大于零，則稱(chēng)函數(shù)f在區(qū)間I上是嚴(yán)格完全單調(diào)函數(shù)的［2，3］.

2 主要結(jié)論及其證明

［1］Abramowitz M，Stegun I A.Handbook of Mathematical Functions with Formulas，Graphs and Mathematical Tables，National Bureau of Standards［M］.Washington：U.S.Government Printing Office，1964.

［2］Mitrinovic D S，Pecaric J E，F(xiàn)ink A M.Classical and New Inequalities in Analysis［M］.London：Kluwer Academic Publishers，1993.

［3］Atanassov R D，Tsoukrovski U V.Some properties of a class of logarithmically completely Monotonic functions［J］.C.R.Acad.Bulgare Sci.，1988，41（2）：21-23.

［4］Qi F，Guo B N.Complete monotonicities of functions involving the gamma and digamma functions［J］. Rgmia Res.Rep.，2004，7（1）：63-72.

［5］Widder D V.The Laplace Transform［M］.Princeton：Princeton University Press，1941/1946.

［6］Guo S，Qi F.Srivastava H M.Supplements to a class of logarithmically completely monotonic functions associated with the gamma function［J］.Applied Mathematics and Computation，2008，197（2）：768-774.

［7］Guo S，Srivastava H M.A class of logarithmically completely monotonic functions［J］.Applied Mathematics Letters，2008，21（11）：1134-1141.

［8］Gradshteyn I S，Ryzhik（eds.）I M.Tables of Integrals，Series，and Products［M］.NewYork and London：Academic Press，2000.

［9］Erdélyi A，Magnus W，Oberhettinger F，et al.Higher Transcendental Functions［M］.NewYork，Toronto and London：McGraw-Hill Book Company，1953.

［10］Guo S.Logarithmically completely monotonic functions and applications［J］.Applied Mathematics and Computation，2013，221（9）：169-176.

［11］Guo S，Qi F，Srivastava H M.A class of logarithmically completely monotonic functions related to the gamma function with applications［J］.Integral Transforms and Special Functions，2012，23（8）：557-566.

The logarithmically completely momotonic functions related to the Gamma function with application

Sun Mei
（School of Mathematics，Northwest University，Xi′an710127，China）

In order to improve the logarithmically completely monotonicity and related inequalities of the function Gα，β（x）（where α∈R，β≥0 are parameter）and 1/Gα，β（x）which are defined in（0，∞）.Using Taylor series expansion，the series expansion and integral expression of Gamma function and Psi function，this paper researches the logarithmically completely monotonicity of function Gα，β（x）and 1/Gα，β（x）and expands the sufficient condition.By the logarithmically completely monotonicities，a new inequality is established.Based on the research of the special circumstances，a symmetrical and concise two-side inequality，which estimates the division of factorial andis established.

Gamma function，logarithmically completely momotonic function，sufficient condition，inequality

O174.6

A

1008-5513（2016）02-0212-09

10.3969/j.issn.1008-5513.2016.02.013

2015-12-10.

陜西省自然科學(xué)基金（2010JM1017）.

孫梅（1989-），碩士生，研究方向：特殊函數(shù)論.

2010 MSC:33B15