因材施教在克拉默法則教學中的體現

唐鋒

（常熟理工學院數學與統計學院，江蘇 常熟 215500）

因材施教在克拉默法則教學中的體現

唐鋒

（常熟理工學院數學與統計學院，江蘇 常熟 215500）

針對不同專業以及不同層次的學生，給出不同的證明方法講授克拉默法則，充分調動學生對學習線性代數的興趣。本文主要介紹三種證明方法：行列式方法；矩陣方法；幾何方法。

克拉默法則；矩陣；因材施教

一、引言

克拉默法則是行列式性質的一個典型應用。內容如下：

定理（克拉默法則）如果線性方程組

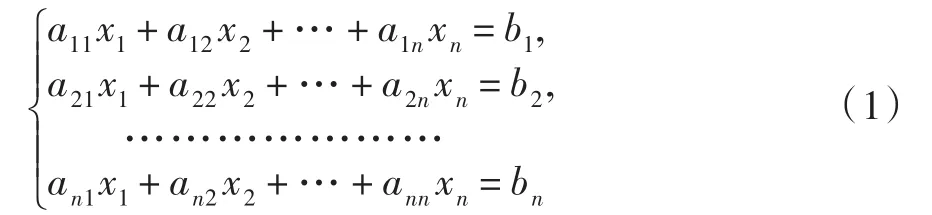
教師在講解克拉默法則時一般都是直接給出定理，接著按照教材［1］的證明順序首先證明方程解的存在性，再證明唯一性。這很不符合一般本科一年級學生的思維習慣，學生在中學學習解方程總是先求解再驗證解的正確性；再者，學生從心底里不愿意接受直接將解代入方程驗證，因為他們沒有弄清楚這個解是怎么得到的；最后，在教材證明中求和符號“∑”大量使用，純推理，沒有直觀感受的大多數學生不感興趣。時間長了，多數學生就會對這門課程產生抵觸情緒，從而使教學過程陷入惡性循環。

筆者所在單位是一所省屬一般理工類院校，所授學生有屬于數學專業、對數學要求較高的信息及電子工程等專業，還有對理論推導要求不高的經濟管理專業等。在多年的教學中，筆者嘗試根據不同類型的學生設計不同的講授，既讓學生拓寬了視野，又學到了比較新穎的知識，還增加了對這門課的興趣，同時也不讓學生“閑著”，充分調動學生積極思考，動員部分班級學生查閱各種資料，促進學生主動學習。

在引入克拉默法則時，首先應該說明：我們已經完成了行列式性質的學習，清楚了行列式的多種計算方法，但是行列式的應用在哪里呢？本節就介紹行列式的一個應用：線性方程組的求解。然后引導學生回憶行列式是如何引進的，學生回答：行列式是通過中學求解二元和三元一次方程組，看出解中分母的規律而引出定義的。此時引導學生往另外一個方向思考：我們已經知道二元和三元一次方程組的解形式都有一種很強的規律，那么將方程組的未知數變量增加到n個，方程的個數也增加到n，此時該線性方程組如何求解呢？這就是本節所要解決的主要內容。

二、行列式證明方法

分析定理中包含了三個結論：1.方程組有解；2.方程組解唯一；3.方程組的解可通過定理中的形式給出。

對于數學專業的學生，要求加強培養其推理能力，為此給出三種行列式的證明方法。

這樣的證明并沒有起到簡化作用，但是延承了學生的思維習慣，所以學生較容易接受。

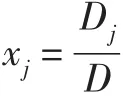
證法2對于1≤j≤n，因為

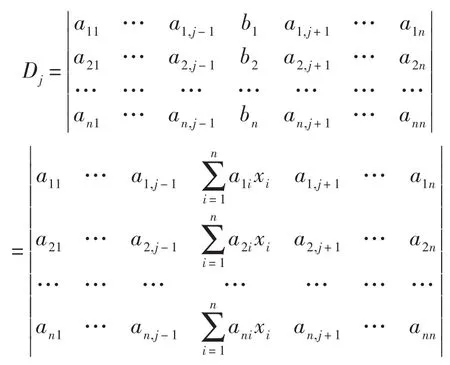
上述行列式的第k列乘(-xk)（k=1,…,j-1,j+1,…,n）加到第j列，得到

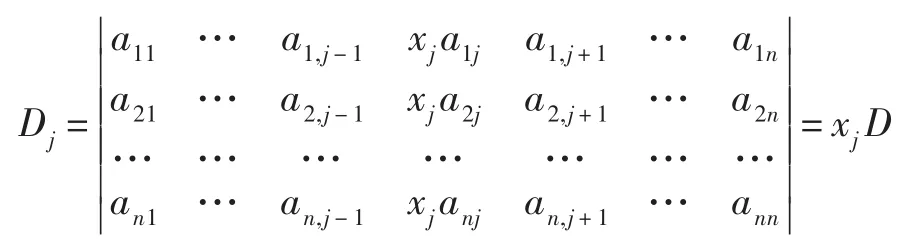
可以發現，證法2比證法1要優越很多。證明題的思路經常是要從結論中尋找線索，這符合學生的思維方式，數學專業的學生也比較喜歡這樣的理論推理。而且證明過程很簡短，關鍵是還用到了行列式的性質，很好地體現了學以致用、學有所用的教學要求。

教材［2］提供了克拉默法則的另外一種行列式的證明，為體現完整性，在此一并給出。

證法3考察有兩行相同的n+1階行列式

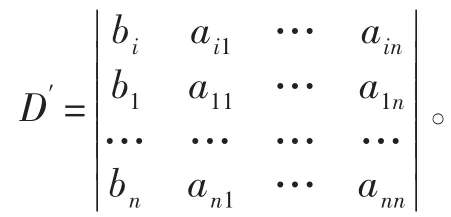
顯然D′=0。D′的第一行中aij的代數余子式為

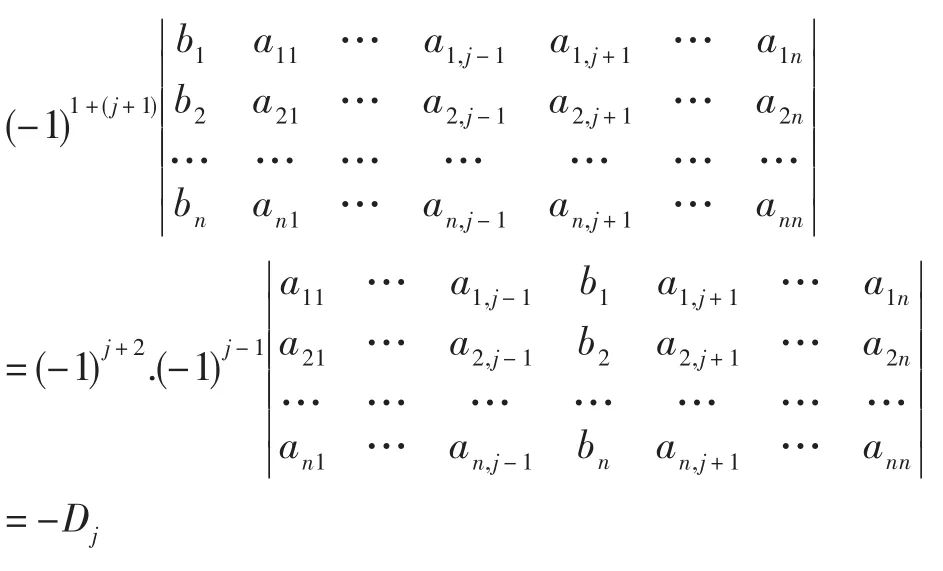
D′按照第一行展開，于是得到0=D′=biD-ai1D1-…-ainDn，即

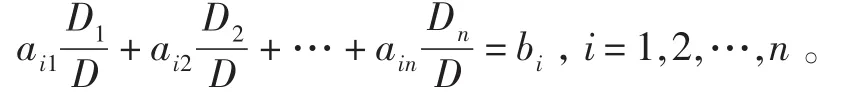
注意證法3只給出了定理中解的存在性證明，但沒給出唯一性的證明，所以證明是不完整的。學生比較很容易發現：證法2在三種證明中是最好的。

三、矩陣證明方法

對于非數學專業但又對數學要求較高的學生，筆者嘗試用矩陣證明的方法講授給學生，介紹如下。

證法4首先按照教材［3］在第二章的證明方法講授。線性方程組（1）可以用矩陣形式表示為

其中A=(aij)n×n,X=(x1,x2,…,xn)T,β=(b1,b2,…,bn)T。

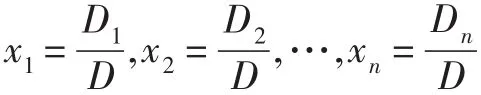
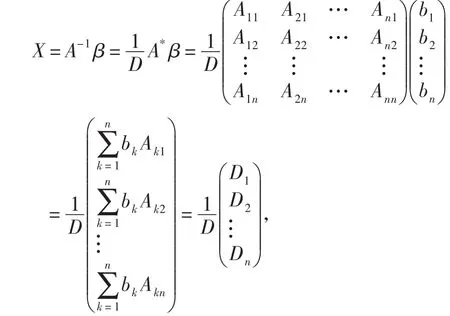
這是很多線性代數教材中的證法，筆者不因循守舊，為拓寬學生的視野及思路，介紹如下的證明方法。

一是構建事業平臺。智庫要有事情做，有研究的問題、項目、課題等，要有相關的科學有效的理論、方法、信息、手段等的支持，也要有專業、有水平團隊支撐；

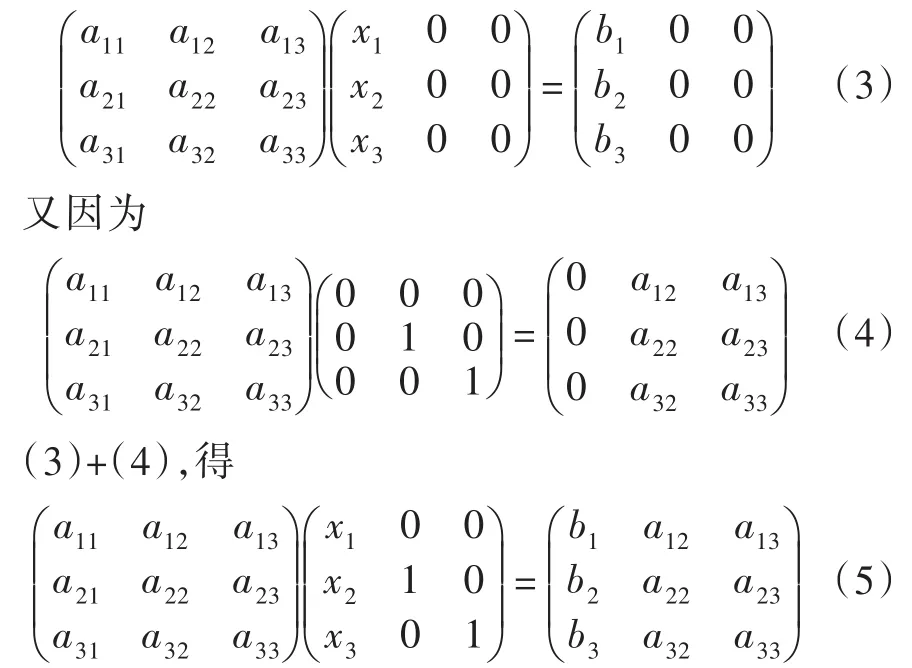
對于非數學專業的學生，這樣的證明已經足夠，工科學生一般是要學會應用，理論推導應該少講，但也不能完全不講，證法5非常適合這類專業的學生。另外，證法5也是很多國外教材使用的方法，筆者介紹給學生也是為了使學生了解國外教材的經典方法，從而拓寬其視野。對于經濟管理類的學生因為學時較少，理論基本可以不講，只需要證法4就能完全滿足學生的需要，其他的方法可以講義的形式發給學生閱讀，或者布置為作業，讓學生查閱資料。

四、幾何證明方法

目前很多大專院校已經將線性代數與解析幾何合并為一門課程，但是部分教材只是代數與幾何內容機械的穿插，并沒有很好結合。為使我校統計專業的學生能真正體會到代數與幾何的有機結合，筆者介紹用幾何方法證明克拉默法則。

首先讓學生理解行列式的幾何意義（以下的介紹可見文獻［5］）。

當n=1時，一階行列式就是一個實數a，它在數軸上表示以原點為起點，實數a為標點的終點的有向線段的有向長度，顯然a＞0時，該有向長度為正；a＜0時，該有向長度為負；a=0時，該有向長度為零。

當n=3時，行列式是“平行六面體的有向體積”，可參看教材［4］，這里不再贅述。

證法6[5]為方便敘述，僅就n=2時給出證明。此時方程組（1）變為

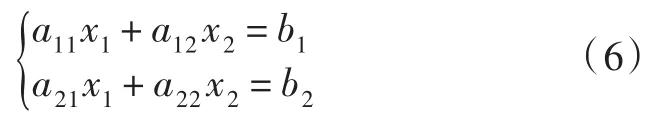
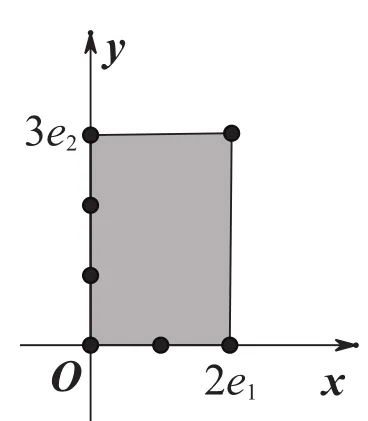
圖1

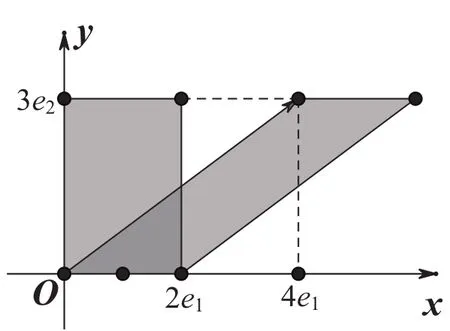
圖2

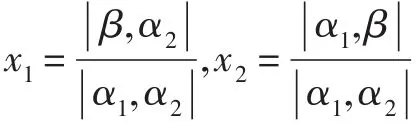
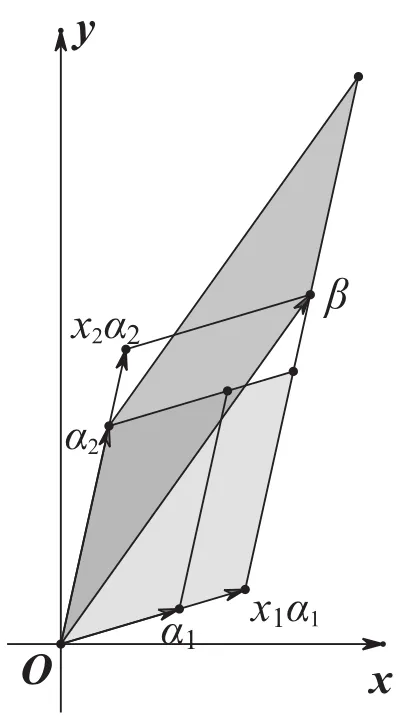
圖3

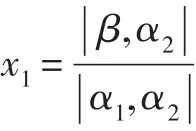
可以看出，證法6完全依靠幾何的直觀理解就可證明，并且此直觀理解可推廣到一般n維空間的形式。作為練習，可請學生板演x2的求解，作為思考題，可布置學生用幾何圖形證明n=3的情形。一個完全是代數的問題在n=2或n=3時可以用純幾何的方法證明，這很好體現了線性代數與解析幾何的有機結合，達到了教學目的。

五、結語

克拉默法則還有許多的證明方法，例如用矩陣的初等變換證明［6］等，這里不再敘述。另外還應指出的是，克拉默法則只是解決了一類特殊的線性方程組的求解問題，對于更一般的線性方程組求解并沒有解決，這為后續內容打下了很好的伏筆。

這些不同的嘗試，對于本節知識的掌握乃至提高學生對這門課的學習興趣產生了良好的效果。總之，因材施教需要教師鉆研教材，善于了解熟悉學生的學習能力，更需要課后閱讀大量的文獻資料，這樣才能真正提高教學水平，讓學生學到更多更好的知識。

［1］北京大學數學系代數小組.高等代數［M］.3版.北京：高等教育出版社，2003：83-86.

［2］同濟大學數學系.線性代數［M］.3版.北京：高等教育出版社，2004：22-26.

［3］同濟大學數學系.線性代數［M］.5版.北京：高等教育出版社，2007：53-54.

［4］呂林根，許子道.解析幾何［M］.4版.北京：高等教育出版社，2006：53-58.

［5］謝琳，張靜.從幾何直觀理解行列式與Cramer法則［J］.高等數學研究，2009（1）：12.

［6］孫伯奎.克萊姆法則的一個新證明［J］.山東大學學報（理學版），2003（2）：38.

Teaching Students in Accordance with Their Aptitude Embodying Cramer Rule in Teaching

TANG Feng
(School of Mathematics and Statistics,Changshu Institute of Technology,Changshu 215500,China)

According to different majors and different levels of the students,this paper gives several ways to prove Cramer rule,which can fully mobilize students'interest in learning linear algebra.The paper mainly introduces three methods to prove the determinant method,matrix method and geometric method.

Cramer Rule;Matrix;teaching students in accordance with their aptitude

O151.2；G424.21

A

1008-2794（2016）06-0102-04

2015-10-14

唐鋒（1973—），男，江蘇泰興人，副教授，碩士，主要研究方向為有限群。