某型陀螺儀自然貯存壽命評估與加速壽命試驗(yàn)時(shí)間預(yù)估

王長安，牛躍聽，穆希輝，羅 賡

（1. 中國白城兵器試驗(yàn)中心，白城 137001；2. 軍械技術(shù)研究所，石家莊 050003；3. 中國華陰兵器試驗(yàn)中心，華陰 714200）

某型陀螺儀自然貯存壽命評估與加速壽命試驗(yàn)時(shí)間預(yù)估

王長安1，牛躍聽2，穆希輝2，羅 賡3

（1. 中國白城兵器試驗(yàn)中心，白城 137001；2. 軍械技術(shù)研究所，石家莊 050003；3. 中國華陰兵器試驗(yàn)中心，華陰 714200）

某型陀螺儀是影響武器控制艙貯存壽命的薄弱環(huán)節(jié)，針對歷年統(tǒng)計(jì)的陀螺儀的成敗型、不完全故障數(shù)據(jù)，將“保序回歸”和“變樣本Pearson χ2擬合優(yōu)度檢驗(yàn)與極小卡方估計(jì)”相結(jié)合，得到了其壽命分布函數(shù)。結(jié)果顯示，I型極大值和威布爾分布適用于陀螺儀的壽命分布，但I(xiàn)型極大值不具有可加速性，因而選擇威布爾分布作為壽命分布。根據(jù)統(tǒng)計(jì)數(shù)據(jù)計(jì)算，得到了置信度0.90和可靠度0.95時(shí)陀螺儀自然貯存壽命為22.30年，得到了陀螺儀在90℃下的加速系數(shù)K=7.2695，預(yù)估了2009年和2011年生產(chǎn)的陀螺儀加速壽命試驗(yàn)時(shí)間分別為8.25月和11.56月，對加速壽命試驗(yàn)時(shí)間規(guī)劃、經(jīng)費(fèi)預(yù)算具有工程實(shí)際意義。

陀螺儀；自然貯存；成敗型數(shù)據(jù)；保序回歸；加速系數(shù)

陀螺儀是武器慣導(dǎo)平臺關(guān)鍵部件，其顯著特點(diǎn)是長期貯存，一次使用。圍繞武器系統(tǒng)關(guān)鍵部組件貯存壽命的評估問題是近年來研究熱點(diǎn)之一。由于研制進(jìn)度和研制經(jīng)費(fèi)等因素的制約，應(yīng)用于我國某型武器上的陀螺儀未進(jìn)行系統(tǒng)科學(xué)的壽命試驗(yàn)，致使不能夠準(zhǔn)確掌握其壽命變化規(guī)律。歷經(jīng)9年多的檢測數(shù)據(jù)統(tǒng)計(jì)證明：陀螺儀是影響該型武器控制艙貯存壽命的薄弱環(huán)節(jié)，迫切需要在其自然貯存檢測數(shù)據(jù)分析的基礎(chǔ)上，抽取一定數(shù)量的陀螺儀，開展加速壽命試驗(yàn)[1]。

如果沒有長期貯存期間的檢測數(shù)據(jù)，通常在一些假設(shè)前提條件下，采用加速壽命試驗(yàn)的方法，預(yù)估其壽命[2-7]。某型陀螺儀貯存于我國亞濕熱、亞干熱、溫和、干燥、寒冷5個(gè)典型氣候環(huán)境區(qū)域的X個(gè)倉庫，至今已貯存9年多時(shí)間，期間積累了大量的檢測數(shù)據(jù)。自然貯存使陀螺儀受到各種環(huán)境因素的綜合作用，可以真實(shí)、直觀地反映其在多環(huán)境應(yīng)力作用下的性能變化規(guī)律[8]。因此，基于自然貯存數(shù)據(jù)分析的加速壽命試驗(yàn)方法更為科學(xué)準(zhǔn)確[9]。

本文從陀螺儀自然貯存檢測數(shù)據(jù)分析中得到其壽命分布函數(shù)，同時(shí)結(jié)合貯存應(yīng)力影響因素得到其加速系數(shù)，預(yù)估其在一定應(yīng)力水平下的加速壽命試驗(yàn)時(shí)間，對加速壽命試驗(yàn)的時(shí)間預(yù)估和費(fèi)用預(yù)算具有很強(qiáng)的工程實(shí)踐指導(dǎo)意義。

1 數(shù)據(jù)描述

本研究中陀螺儀的檢測數(shù)據(jù)屬于成敗型不完全數(shù)據(jù)，數(shù)據(jù)類型可以等效如下：

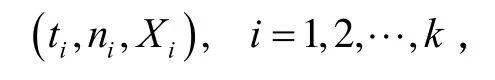
在實(shí)際工作中：一方面受時(shí)間和費(fèi)用等約束，檢測試驗(yàn)開展得不夠徹底，因而試驗(yàn)結(jié)果受試驗(yàn)的隨機(jī)性影響很大；另一方面，陀螺儀屬于高可靠性產(chǎn)品，失效率很低，故雖然檢測樣本量很大，但失效數(shù)很少，有時(shí)會(huì)出現(xiàn)的情況，這與失效概率隨時(shí)間增加而降低的特性不相符合，工程上稱之為數(shù)據(jù)的“倒掛”，嚴(yán)重的倒掛會(huì)使計(jì)算結(jié)果產(chǎn)生很大偏差。

2 評估方法

針對陀螺儀的不完全貯存壽命試驗(yàn)數(shù)據(jù)，采用極小卡方估計(jì)法（IRMCE）進(jìn)行評估。在極小卡方估計(jì)法運(yùn)用過程中，將保序回歸的思想應(yīng)用于陀螺儀貯存壽命試驗(yàn)數(shù)據(jù)的分析中，用于調(diào)整失效頻率由于隨機(jī)性而產(chǎn)生的“倒掛”，并結(jié)合 Pearson擬合優(yōu)度理論處理試驗(yàn)數(shù)據(jù)，給出分布參數(shù)及可靠壽命的估計(jì)，同時(shí)對分布函數(shù)進(jìn)行檢驗(yàn)。我們假設(shè)其壽命分布的可能形式有指數(shù)分布族、威布爾分布族、極值分布族、對數(shù)正態(tài)分布族。

2.1 失效頻率 fi的保序回歸

在貯存壽命試驗(yàn)中，ti時(shí)刻樣本的失效頻率為一個(gè)有限集合，為定義在T上的一有界函數(shù)。若T上又定義了一種半序關(guān)系“?”，且對，均有成立，則稱函數(shù)為定義在T上相對于的保序函數(shù)。記G為保序函數(shù)的全體，若存在f*∈G，滿足：

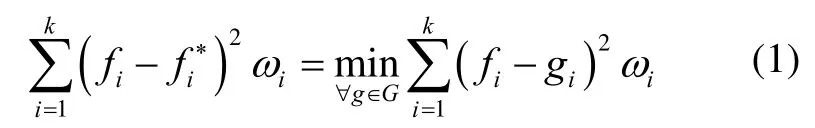
2.2 極小卡方估計(jì)與變樣本Pearson2χ?jǐn)M合優(yōu)度檢驗(yàn)

極小卡方估計(jì)是指將極小化Pearson2χ統(tǒng)計(jì)量所得到的參數(shù)作為真值的最佳估計(jì)，即：

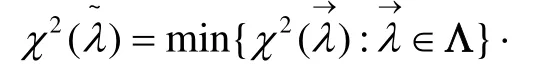
通過解方程組

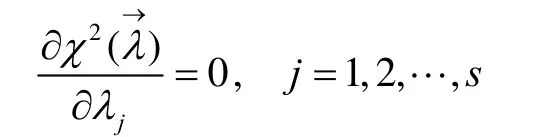
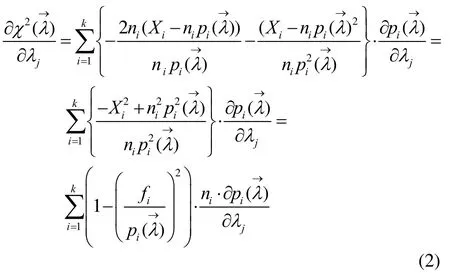
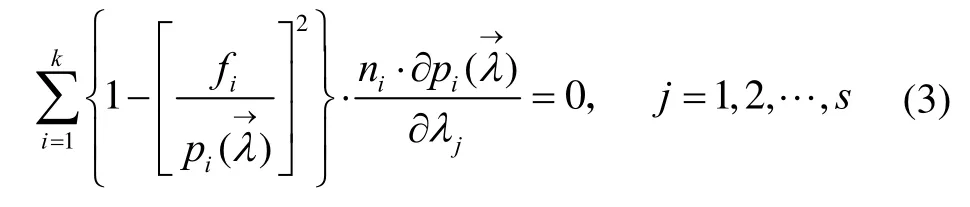
在擬合優(yōu)度檢驗(yàn)的相關(guān)理論中，Pearson提出了2χ統(tǒng)計(jì)量用于檢驗(yàn)一組獨(dú)立樣本的共同分布是否屬于某一具有特定性質(zhì)的分布族，其中變樣本復(fù)合Pearson2χ統(tǒng)計(jì)量的形式為

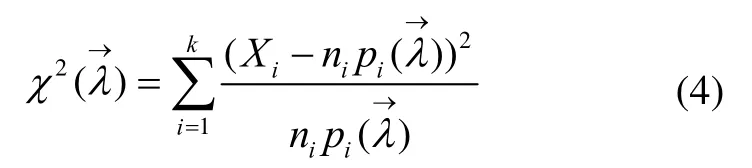
Pearson2χ統(tǒng)計(jì)量描述了期望頻數(shù)與觀察頻數(shù)之間的差異。當(dāng)ni→∞時(shí)，的極限分布是自由度

為k-1的2χ分布，即。在進(jìn)行檢驗(yàn)時(shí)，真值未知，一個(gè)自然的想法是用的估計(jì)量代替計(jì)算，即用

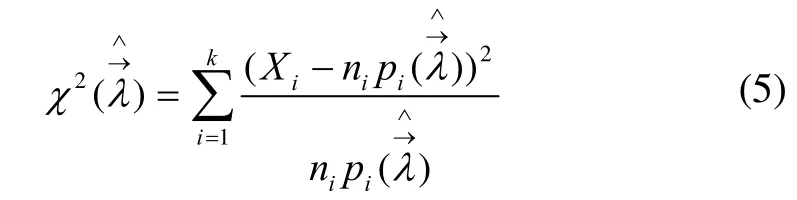
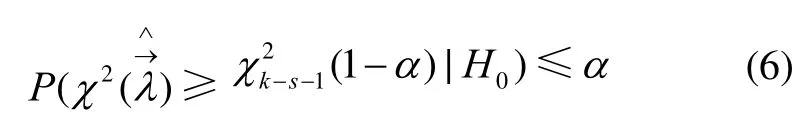
3 自然貯存陀螺儀故障統(tǒng)計(jì)分析

對自然環(huán)境中貯存30個(gè)月到113個(gè)月的陀螺儀樣本進(jìn)行性能檢測，檢測結(jié)果如表1，數(shù)據(jù)處理結(jié)果如表2。

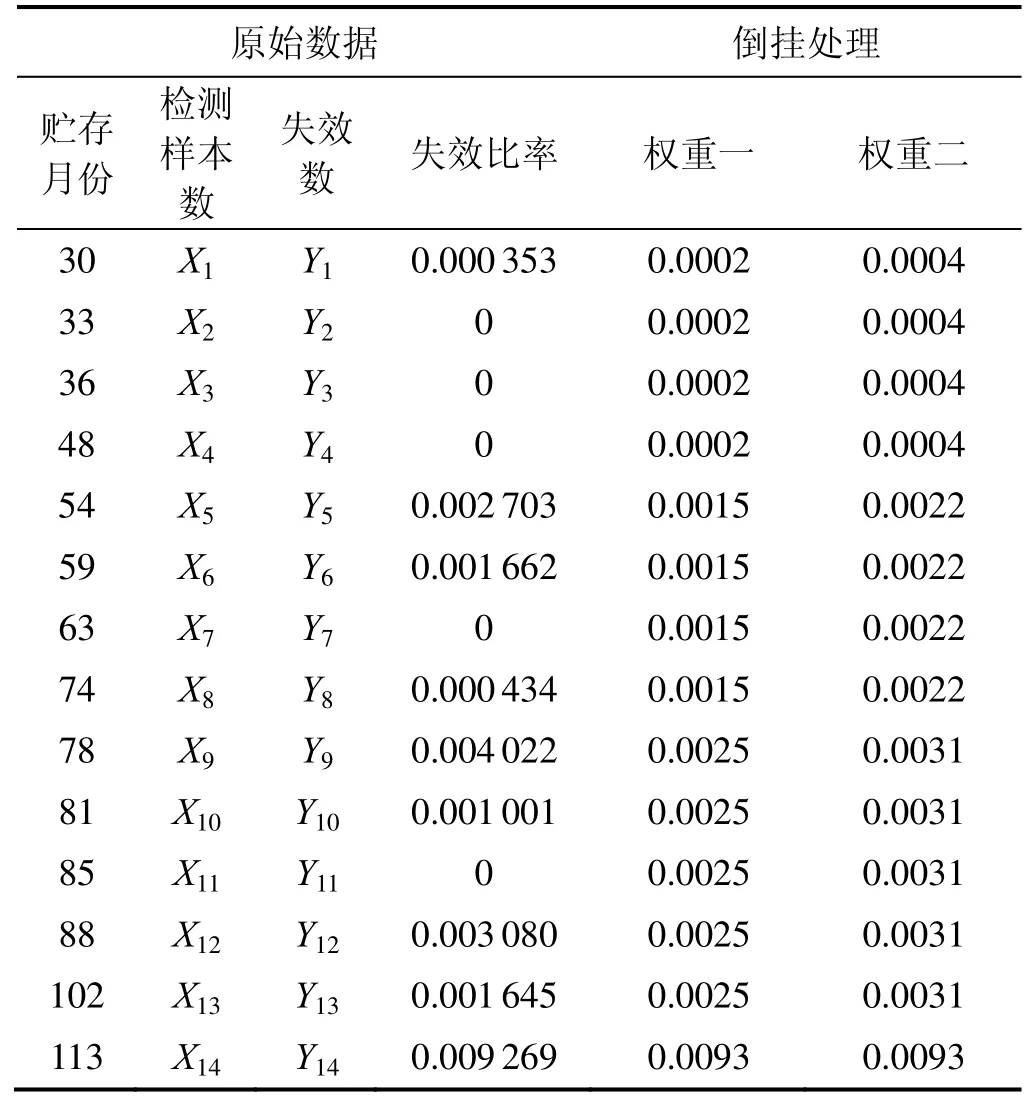
表1 陀螺儀故障統(tǒng)計(jì)表Tab.1 Statistics of gyroscope failure

表2 陀螺儀數(shù)據(jù)分析結(jié)果Tab.2 Analysis results of gyroscope data

4 結(jié) 論

4.1 壽命失效分布函數(shù)

在前文分析中，可以看出壽命分布服從威布爾分布和I型極大值分布時(shí)得到的分布參數(shù)以及可靠壽命更符合實(shí)際。下面對威布爾分布和I型極大值分布的可加速性進(jìn)行驗(yàn)證。對于壽命模型，加速系數(shù)存在，才具有可加速性。

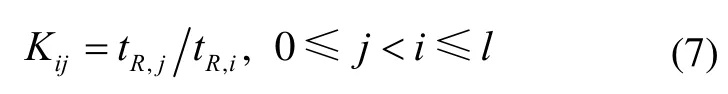
稱為在加速應(yīng)力水平Si對應(yīng)力水平Sj的 R可靠壽命的加速系數(shù)，簡稱加速系數(shù)。

由定義可知，加速系數(shù)不僅與 Si、 Sj下產(chǎn)品的分布參數(shù)有關(guān)，而且還與所選的可靠度R有關(guān)。但是真正能用于工程實(shí)踐的有效的加速壽命試驗(yàn)會(huì)非常自然地要求加速系數(shù)是與R無關(guān)的（僅由 Si、 Sj下產(chǎn)品的分布參數(shù)確定）常數(shù)。否則隨著試驗(yàn)的進(jìn)展，工作時(shí)間的延長，R逐漸變小，加速系數(shù)就會(huì)變化，這樣的加速系數(shù)就失去了工程實(shí)踐價(jià)值。

1）壽命t服從威布爾分布（威布爾分布為 III型極小值分布的特殊情況）時(shí)，累計(jì)失效函數(shù)為

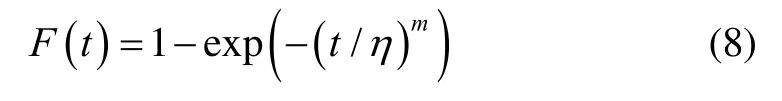
式中：η為特征壽命；m為形狀參數(shù)。

令y=lnt，則轉(zhuǎn)化為I型極小值分布，其累積失效函數(shù)為

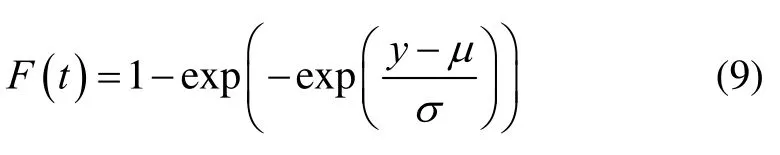
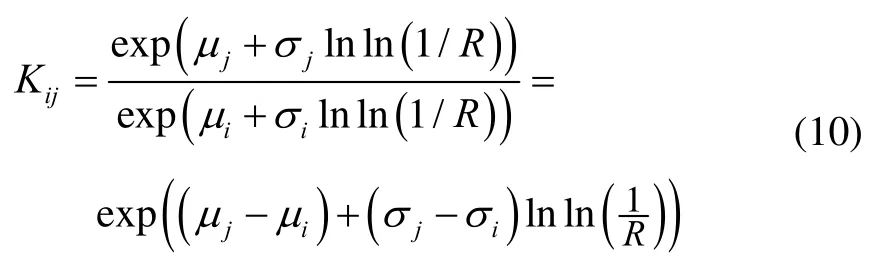
要求加速系數(shù)與可靠度R無關(guān)，即要求：

σi=常數(shù)，i=0, 1, 2, ... , l；

2）壽命t服從I型極大值分布，其累積失效函數(shù)為

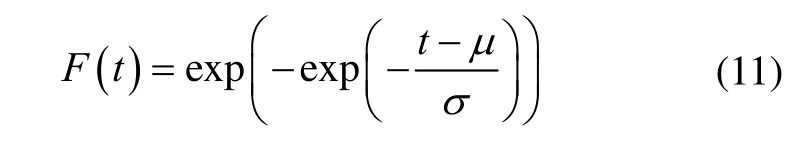
式中：μ為位置參數(shù)；σ為尺度參數(shù)。可靠壽命為

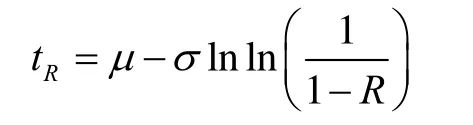
加速系數(shù)為

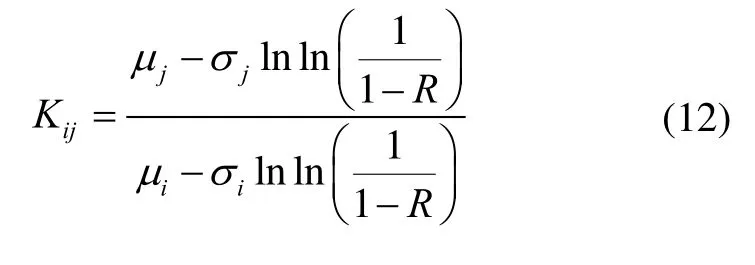
要求加速系數(shù)與可靠度R無關(guān)，即要求：

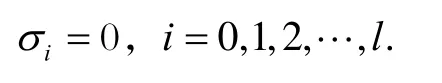
故I型極大值分布的加速系數(shù)不存在，不能應(yīng)用于加速壽命備選分布。

綜上所述，選取威布爾分布為陀螺儀壽命分布函數(shù)：

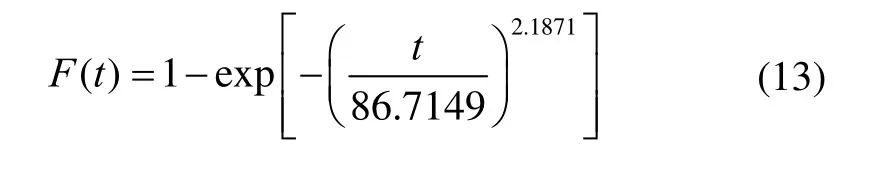
4.2 加速模型及加速系數(shù)

陀螺儀貯存?zhèn)}庫的溫度范圍為（5℃～30℃），其在不同溫度應(yīng)力下的失效有一定規(guī)律性，陀螺儀的壽命模型選擇威布爾函數(shù)作為分布函數(shù)。

由本文上述分析方法，可以得到陀螺儀在不同溫度下的威布爾分布參數(shù)?η以及可靠壽命t0.95：

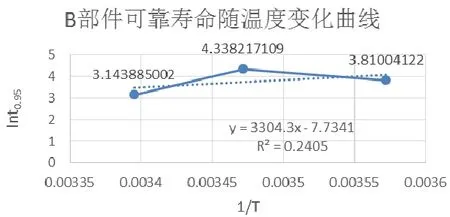
即，陀螺儀的加速方程為Arrhenius方程：

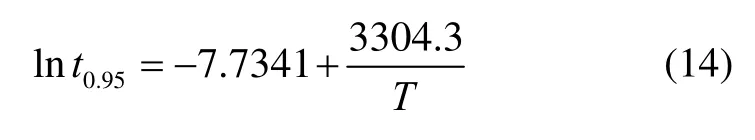
當(dāng)常溫選25℃，加速壽命試驗(yàn)的溫度應(yīng)力分別選90℃、110℃、135℃時(shí)，不難得到其加速系數(shù)如下[12]：

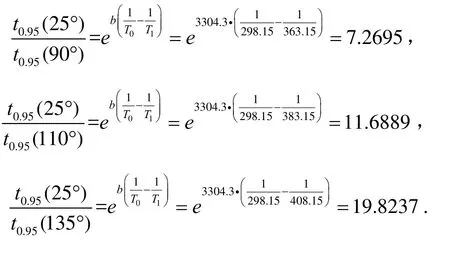
生產(chǎn)廠家給出陀螺儀在常溫下的貯存壽命為 10年，那么其在90℃的的條件下，加速壽命試驗(yàn)的時(shí)間大約為：10/7.2695=1.3756年=16.5073月。

經(jīng)專家論證，陀螺儀的試驗(yàn)樣本取自分布于我國不同氣候區(qū)的控制艙最為科學(xué)[13]。例如，預(yù)計(jì) 2009年和2011年生產(chǎn)的陀螺儀的加速壽命試驗(yàn)時(shí)間如表3所示。

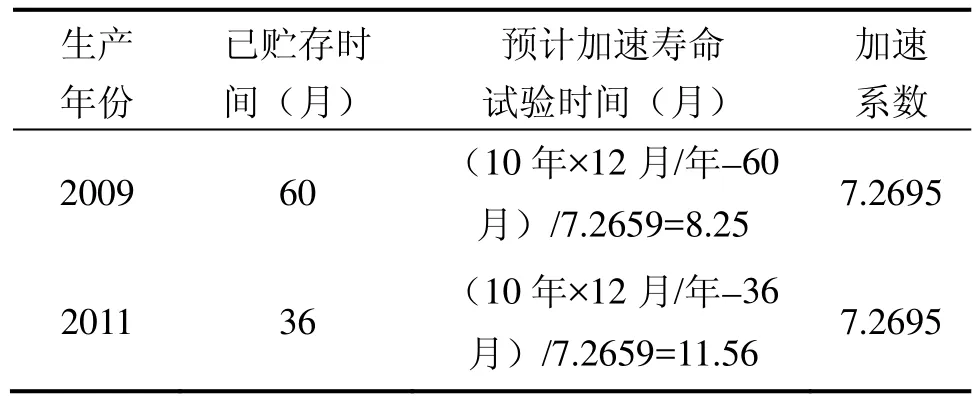
表3 加速壽命試驗(yàn)時(shí)間Tab.3 ALT time

在制定詳細(xì)的加速壽命試驗(yàn)方案時(shí)，應(yīng)參考以上的預(yù)估結(jié)果，以便合理選擇應(yīng)力水平，預(yù)估試驗(yàn)時(shí)間和費(fèi)用。

（References）：

[1]羅賡, 穆希輝, 牛躍聽, 等. 小子樣條件下某型加速度計(jì)步降加速壽命試驗(yàn)優(yōu)化設(shè)計(jì)[J]. 中國慣性技術(shù)學(xué)報(bào),2015, 23(5): 696-700.Luo Geng, Mu Xi-hui, Niu Yue-ting. Optimal design method for accelerometer step-down-stress accelerated life testing on condition of small sample[J]. Journal of Chinese Inertial Technology, 2015, 23(5): 696-700.

[2]袁宏杰, 李樓德, 段剛, 等. 加速度計(jì)貯存壽命與可靠性的步進(jìn)應(yīng)力加速退化試驗(yàn)評估方法[J]. 中國慣性技術(shù)學(xué)報(bào), 2012, 20(1): 113-116.Yuan Hong-jie, Li Lou-de, Duan Gang, et al. Storage life and reliability evaluation of accelerometer by step stress accelerated degradation testing[J]. Journal of Chinese Inertial Technology, 2012, 20(1): 113-116.

[3]Jinsuk Lee, Rong Pan. Analyzing step-stress accelerated life testing data using generalized linear models[J]. IIE Transactions, 2010, 42(8): 589-598.

[4]Suk Joo Bae, Seong-Joon Kim, Jong In Park, et al.Lifetime prediction through accelerated degradation testing of membrane electrode assemblies in direct methanol fuel cells[J]. International Journal of Hydrogen Energy, 2010, 35: 9166-9167.

[5]Wohlgemuth J H, Kurtz S. Using accelerated testing to predict module reliability[C]//37thIEEE Photovoltaic Specialists Conference. 2011.

[6]Li Xiao-yang, Jiang Tong-min. Optimal design for stepstress accelerated degradation with competing failure modes[C]//Annual Reliability and Maintainability Symposium. 2009: 64-68.

[7]Ismail A A. Estimating the parameters of Weibull distribution and the acceleration factor from hybrid partially accelerated life test[J]. Applied Mathematical Modelling, 2012, 36(7): 2920-2925.

[8]Takada A, So N, Hajime I. A new acceleration factor decision method for ICCG method based on condition number[J]. IEEE Transactions on Magnetics, 2012, 48(2):519-522.

[9]牛躍聽, 穆希輝, 姜志保, 等. 自然貯存環(huán)境下某型加速度計(jì)貯存壽命評估[J]. 中國慣性技術(shù)學(xué)報(bào), 2014,22(4): 552-556.Niu Yue-ting, Mu Xi-hui, Jiang Zhi-bao, et al. Storage life assessment of an accelerometer under natural storage environment[J]. Journal of Chinese Inertial Technology,2014, 22(4): 552-556.

[10]史寧中. 保序回歸與最大似然估計(jì)[J]. 應(yīng)用概率統(tǒng)計(jì),1993, 9(2): 203-214.Shi Ning-zhong. Isotonic regression and estimation of normal distribution[J]. Acta Mathematicae Applicatae Sinica, 1993, 9(2): 203-214.

[11]Balakrishnan N, Beutner E, Kateri M. Order restricted inference for exponential step-stress models[J]. IEEE Transactions on Reliability, 2009, 58(1): 132-142.

[12]申?duì)幑? 苑景春, 董靜宇, 等. 彈上設(shè)備加速壽命試驗(yàn)中加速因子估計(jì)方法[J]. 系統(tǒng)工程與電子技術(shù), 2015,37(8): 1948-1951.Shen Zheng-guang, Yuan Jing-chun, Dong Jing-yu, et al.Research on acceleration factor estimation method of accelerated life test of missile-borne equipment[J]. System Engineering and Electronics, 2015, 37(8): 1948-1951.

[13]牛躍聽, 穆希輝, 姜志保. 某型火箭彈控制艙環(huán)境適應(yīng)性研究[J], 裝備環(huán)境工程, 2014, 11(1): 86-92.Niu Yue-ting, Mu Xi-hui, Jiang Zhi-bao, et al. Research on environmental adaptability of guided rocket[J]. Equipment Environmental Engineering, 2014, 11(1): 86-92.

Prediction of storage life and accelerated-life-testing time for gyroscope

WANG Chang-an1, NIU Yue-ting2, MU Xi-hui2, LUO Geng3
(1. Baicheng Weapon Test Center, Baicheng 137001, China; 2. Ordnance Engineering Institute, Shijiazhuang 050003, China; 3. Huayin Ordnance Test Center of China, Huayin 714200, China)

One type of gyroscopes in the control cabin of a rocket could significantly affect the storage life.To solve this problem, the isotonic regression, minimum2χestimation, and Pearson test of goodness-of-fit are combined to get its natural storage reliability distribution function, aiming at the binomial and incomplete of the gyroscope’s statistical data. Test results show that both I maxima distribution and Weibull distribution are applicable for the gyroscope’s life distribution, but I maxima distribution is excluded due to without accelerating ability, and thus Weibull distribution is adopted. Test results show that the natural storage life is 22.30 years when confidence level is 0.90 and reliability is 0.95. The acceleration factor under 90℃ is 7.2695, which is used for forecasting the gyroscope’s accelerated-life-testing time, and they are 8.25 months and 11.56 months respectively when manufactured in 2009 and 2011. It is of technological importance to the engineering practice of accelerated-life-testing time plan and budget.

gyroscope; natural storage; binomial data; isotonic regression; acceleration factor

TJ760.6

A

1005-6734(2016)05-0683-05

10.13695/j.cnki.12-1222/o3.2016.05.022

2016-06-03；

2016-08-29

國家自然科學(xué)基金（61471385）

王長安（1979—），男，工程師。E-mail: 531706356@qq.com

聯(lián) 系 人：牛躍聽（1978—），男，博士后，主要研究方向?yàn)樾畔⒒瘡椝帀勖u估與延壽技術(shù)。E-mail: nyt369@sina.com