一種利用起車過程瞬態振動響應的轉子動力學參數識別方法

張西寧,吳吉利,王奔

(西安交通大學機械制造系統工程國家重點實驗室,710049,西安)

?

一種利用起車過程瞬態振動響應的轉子動力學參數識別方法

張西寧,吳吉利,王奔

(西安交通大學機械制造系統工程國家重點實驗室,710049,西安)

在分析轉子系統起動過程的振動響應組成和振動響應信號中出現拍振現象成因的基礎上,提出了一種基于起車過程瞬態振動響應的轉子動力學參數時域識別方法。以轉子系統起動過程中的失衡振動響應信號替代頻域參數識別法中的正弦掃描激振響應信號,來識別轉子系統固有頻率和阻尼參數的時域信號,同時給出了參數估計原理,并利用仿真信號和實驗測試的起車過程振動響應信號對轉子系統的一階固有頻率和阻尼進行了計算。結果表明:所提出方法利用了轉子起動過程的振動響應信號,其參數識別僅在時域內進行,不需要復雜的激振設備,具有計算簡單、應用前景廣闊等特點。

轉子;起動過程;振動響應;拍振;動力學參數

在現代工業生產中旋轉機械的使用日益廣泛,大型旋轉機械,例如汽輪發電機組、燃氣輪機組、透平壓縮機組、離心泵等均是國民經濟支柱產業中的關鍵設備。轉子系統是旋轉機械的核心,其工作中的振動和穩定性直接影響到整個設備的可靠性、安全性和壽命。轉子系統的參數識別技術一直是該領域國內外研究的熱點。動力學系統參數識別方法可分為兩大類:頻域識別方法和時域識別方法[1-2]。頻域參數識別方法是一種利用動力學系統共振特性的傳統識別方法,要通過正弦掃描激振、瞬態激勵、隨機激勵等及其響應測試來確定各階頻率和阻尼等參數。頻域識別法依賴于傅里葉變換,物理概念清楚、直觀,對測量精度要求不高,抗噪聲能力強,缺點是激振、實驗設備復雜,難以進行在線識別,對于大阻尼和頻率密集的情形無能為力。時域參數識別直接利用振動響應信號的時間曲線來識別振動參數,如Ibrahim時域法[3-5]、最小二乘時域法[6]、隨機減量法[7-9]、隨機子空間法[10-11]等均是常用的時域參數識別方法。時域參數識別不受系統大阻尼及密集頻率的限制,不需要復雜的激振設備,可實現在線識別,但對噪聲敏感,對測量精度要求高。

本文在分析轉子系統起動過程振動響應特性的基礎上,用轉子系統起動過程中的失衡振動響應信號替代頻域參數識別法中的正弦掃描激振響應信號,提出了一種轉子系統固有頻率和阻尼參數的時域識別方法,并給出了參數識別方法的原理,通過對起動響應振動信號的仿真分析和實驗測試,驗證了所提方法的有效性和準確性。

1 起動過程振動響應的拍振現象

對于如圖1所示的垂直軸兩端簡支的轉子系統,軸的質量不計,質量為m的圓盤固定在中間,C是圓盤的質心,D是圓盤的旋轉中心,偏心距CD=e,假設轉子沿X和Y方向的剛度均為k,沿X和Y方向的阻尼均為c,起動過程的振動方程可近似為

(1)

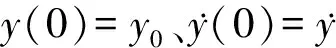
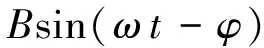
(2)

式中:ωn=(k/m)1/2為無阻尼固有頻率;ζ=c/(2ωnm)為阻尼比;ωd=ωn(1-ζ2)1/2為阻尼固有頻率;λ=ω/ωn為頻率比;B=P/k((1-λ2)2+(2ζλ)2)1/2為振動幅值;P=meω2為激振力;φ=tg-12ζλ/(1-λ2)為相位。式(2)右端的三項分別是系統在無激勵時的自由振動、自由伴隨振動及穩態強迫振動。在初始位移和初始速度均為0的情況下

(3)

顯然,轉子系統從0轉速起動過程中自由伴隨振動依然存在。由于轉子系統升速過程中的激振力始終在變化,所以轉子起動過程的振動響應信號中始終存在自由伴隨振動。圖2是按式(3)得到的轉子起動過程中自由伴隨振動和強迫振動響應信號。

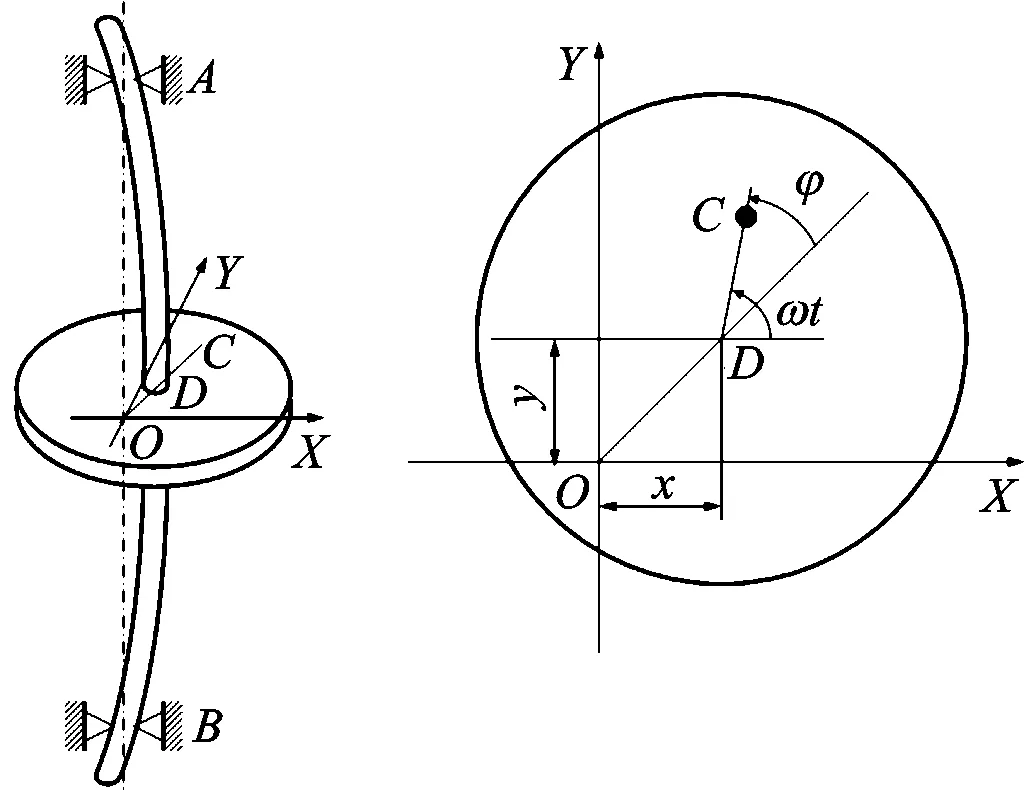
圖1 轉子系統

(a)自由伴隨振動

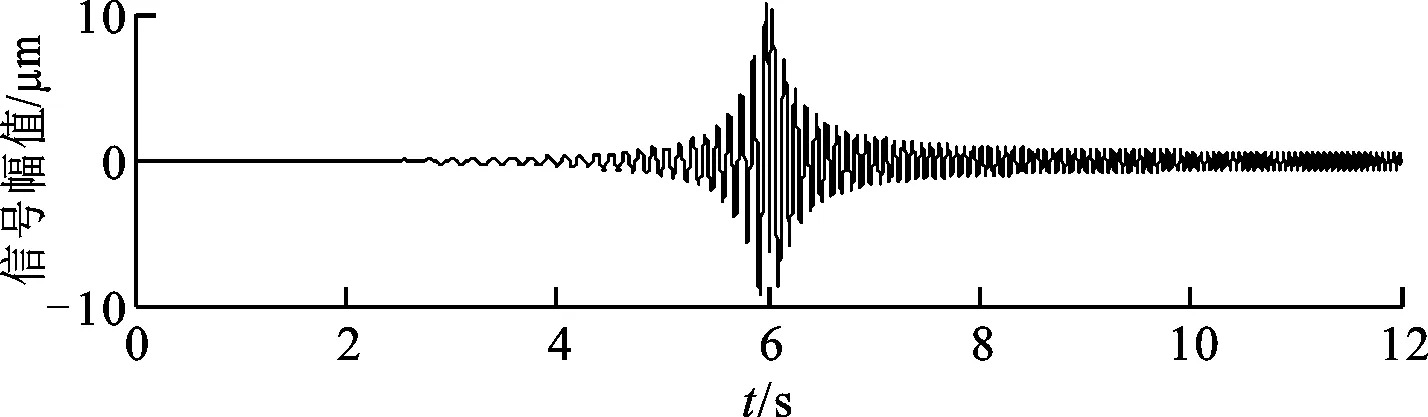
(b)強迫振動響應圖2 轉子起動過程中自由伴隨振動和強迫振動響應信號

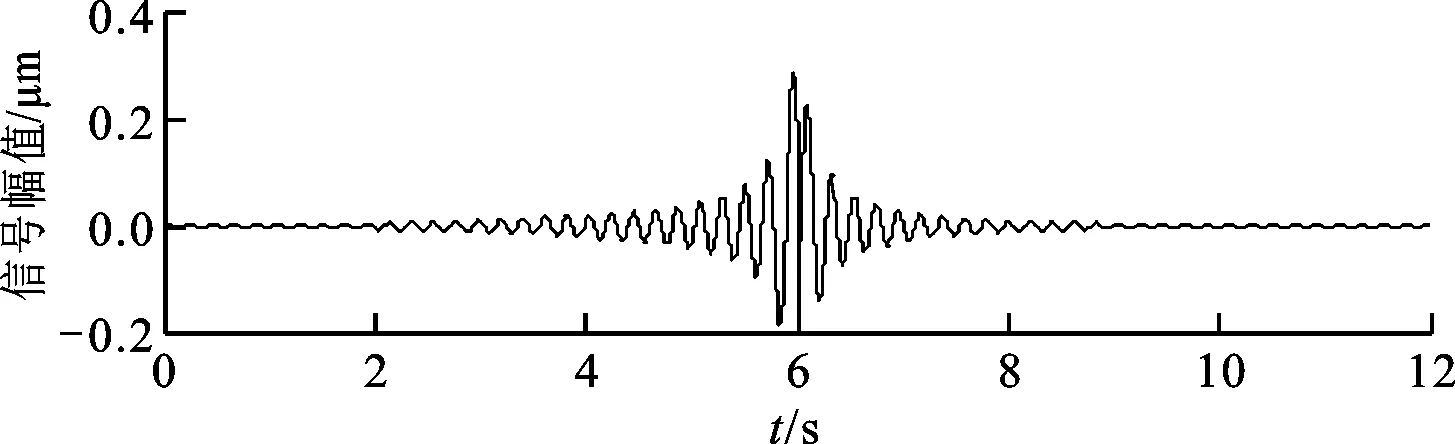
從圖2可以看出,在臨界轉速附近自由伴隨振動幅值和強迫振動響應幅值均存在最大值。根據前面的理論解可知,自由伴隨振動的頻率始終是ωd,而強迫振動響應頻率始終與轉速ω一致。在臨界轉速附近,ωd、ωn、ω三者很接近,由此可推測在過臨界附近轉子系統總的振動響應一定會出現拍振現象。為此,采用Wilson-θ法對一轉子系統的升速過程進行了數值求解。求解設定參數:轉子系統質量為2 500 kg,阻尼比為0.02,無阻尼固有頻率為30 Hz,偏心質量為4 g,偏心距為0.005 m,起始轉頻為1 Hz,升速率為10 Hz/s。求解得到轉子系統起動過程的振動響應信號如圖3所示。

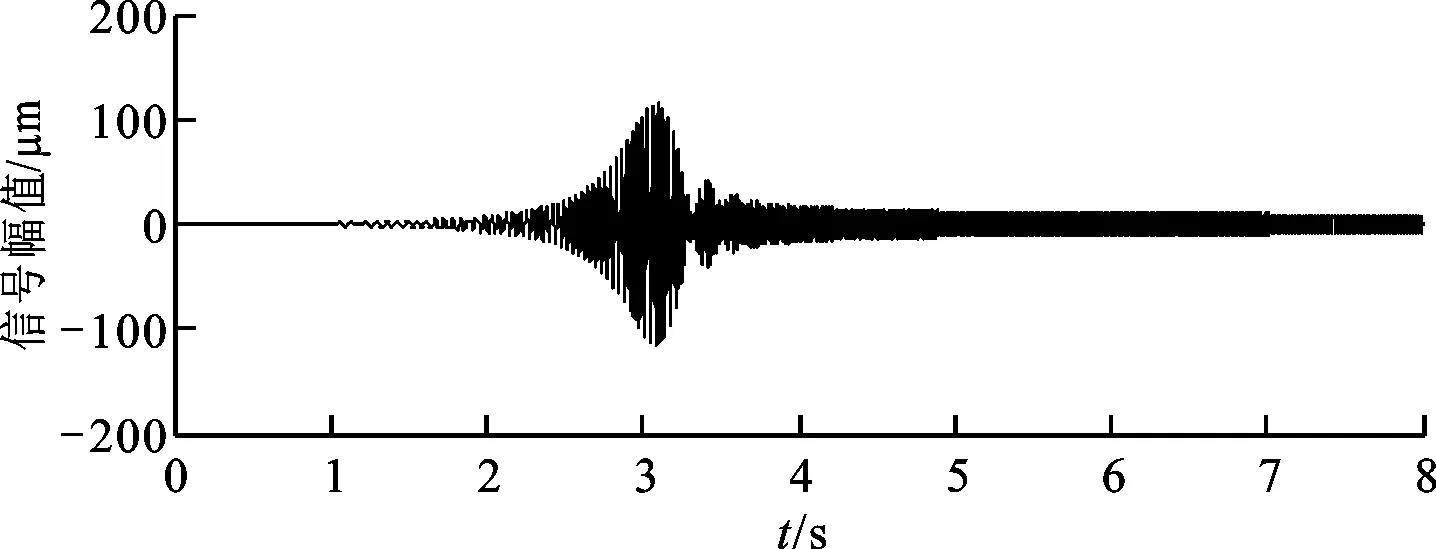
圖3 轉子系統起動過程的振動響應信號

從圖3可以看出,轉子系統在過臨界狀態之后,振動響應出現了明顯的拍振現象,同時振動響應幅值最大處的頻率高于無阻尼固有頻率。其實,轉子系統起動過程的振動響應出現拍振現象是很普遍的,文獻[13-18]在研究航空發動機、渦輪泵、轉子實驗臺等轉子系統起動過程的瞬時動力學特性中均在振動響應上出現了拍振現象,但沒有對拍振現象進行深入的理論分析。將共振區域附近的拍振用于轉子系統動力學參數辨識的方法,還尚未進行過詳細的研究,因此本文探究將轉子起停時瞬態振動響應信號出現的拍振用于轉子系統動力學參數的識別。

2 參數識別原理

起動過程拍振的出現一般在轉子系統過臨界之后,考慮到轉子系統從起動到過臨界需要一段時間,所以忽略式(3)中已經大幅度衰減的無激勵自由振動。設式(3)中的后兩項升速過程振動響應信號中的強迫分量為

(4)

自由伴隨振動分量為

(5)

這樣強迫振動和伴隨振動均可看成是復平面上的旋轉向量在虛軸上的投影。如圖4所示,升速過程中只有在yp(t)和yc(t)相位相同的時刻,合成后的振幅會出現極大值;在yp(t)和yc(t)相位相反的時刻,合成后的振幅會出現極小值。由此可得:振動響應拍峰值出現的條件為θ(t)=γ(t)+2Kπ,K為整數;振動響應拍谷值出現的條件為θ(t)=γ(t)+(2K+1)π。

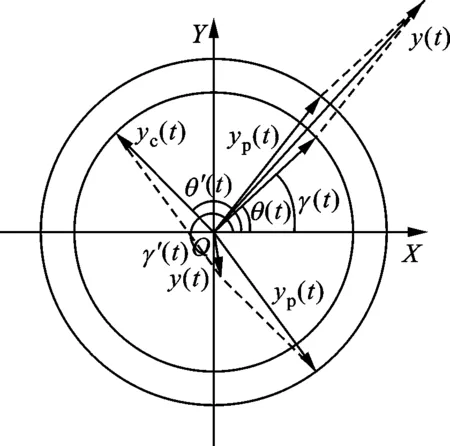
圖4 強迫振動和伴隨振動的合成

起停過程振動響應出現拍振現象顯然與轉子系統的參數密切相關。為了利用振動響應來估計轉子系統的參數,假設起動過程振動響應包絡線上的拍峰值對應的時刻分別為t0、t1、t2等,如圖5所示。

t0時刻的轉速為ω0,升速率為ωm0,t0時刻自由伴隨振動的相位為αt0,強迫振動的相位為βt0。t1時刻自由伴隨振動的相位為αt1,強迫振動的相位為βt1。根據起動過程的振動特征及各個時刻的轉速、升速率可知

(6)

(7)

根據拍峰值出現的條件αt1=βt1、αt0=βt0可得

(8)

(9)

式中:K為整數,K>0表示拍振發生在過臨界之后,K<0表示拍振發生在過臨界之前。當K=1時,兩個相鄰的拍峰值之間的相位關系使得式(7)中的轉速ω0、升速率ωm0、Δt=t1-t0在峰值出現時刻t0和t1可通過振動響應的包絡線獲得,由此獲得轉子系統的阻尼固有頻率ωd。

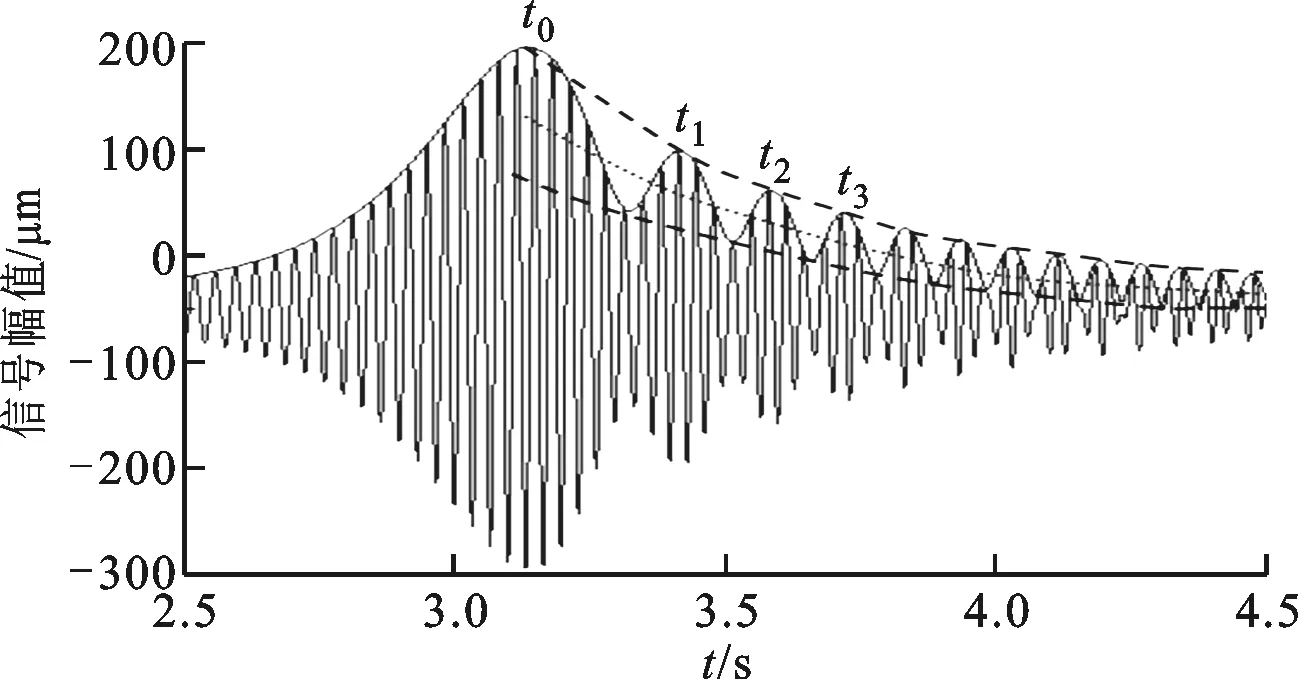
圖5 參數識別原理圖

需要說明的是,以上是基于振動響應包絡線上的峰值點計算的,實際上根據振動響應包絡線上的谷值點也可計算轉子系統的阻尼固有頻率ωd,計算原理和步驟與利用峰值點計算完全一致。

由于振動響應包絡線上的峰值點的幅值是自由伴隨振動幅值與強迫振動幅值的疊加,振動響應包絡線上的谷值點的幅值是自由伴隨振動幅值與強迫振動幅值的差,所以對振動響應包絡線上的峰值點和谷值點分別進行曲線擬合,得到圖5中的兩條隨時間衰減的虛線,即峰值點曲線和谷值點曲線。對峰值點曲線和谷值點曲線進行平均處理得到的中間點線,可看成是強迫振動的幅值衰減曲線,而用峰值點擬合的虛線減去中間的點線得到的曲線,就是自由伴隨振動的衰減曲線。根據式(3)中自由伴隨振動幅值衰減部分,不難得到自由伴隨振動的衰減曲線的表達式,即

(10)

對式(10)兩邊取對數后可得

(11)

這樣,利用自由伴隨振動的衰減曲線,通過矩陣最小二乘法不難計算出阻尼比ζ和阻尼固有頻率ωn。

3 仿真數據分析驗證

為了驗證參數估計的準確性,對采用Wilson-θ法得到的起動過程振動響應信號進行了分析和計算,仿真計算時設定的轉子系統參數詳見第1節。首先,確定振動響應信號上每轉的最大振動幅值點和最小振動幅值點,經過插值處理得到振動響應信號的上下包絡曲線,對上下包絡曲線的絕對值進行平均處理,得到平均幅值包絡曲線。然后,確定平均幅值包絡曲線上的拍峰點和拍谷點,經插值處理后得到峰值點曲線和谷值點曲線,以及峰值點和谷值點的準確時刻。相鄰峰值點或相鄰谷值點的準確時間,以及對應的轉速和升速率計算結果如表1所示。根據式(9)、利用峰值點1和峰值點2對ωd進行估計,估計的ωd=184.028 1 rad/s,該值與仿真計算時設定的188.457 9 rad/s相比,相對誤差為2.37%,如表2所示。

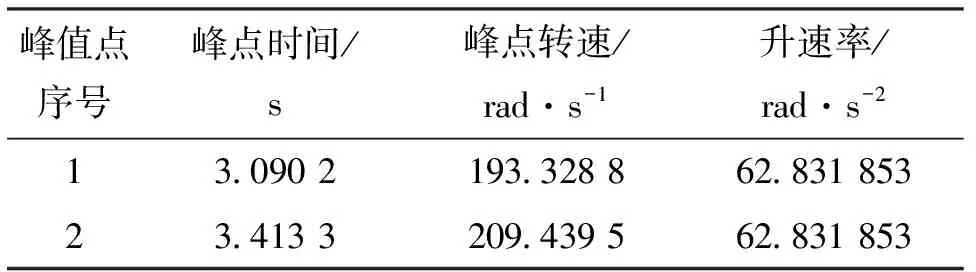
表1 相鄰峰值點準確時刻及對應轉速和升速率計算結果

表2 ωd估計結果

利用峰值點曲線和谷值點曲線計算自由伴隨振動的衰減曲線,再根據式(11)、利用矩陣最小二乘法估計阻尼比和無阻尼固有頻率。估計的阻尼比和無阻尼固有頻率分別為0.026 395和188.523 5rad/s。Wilson-θ法數值計算時采用的阻尼比和無阻尼固有頻率分別為0.02和188.495 6rad/s,由此得到阻尼比和無阻尼固有頻率估計值的相對誤差分別為3.19%和0.015%。從仿真信號的計算結果看,估計值與實際的參數較為接近,表明本文所提轉子系統參數估計方法是可行和有效的。

在轉子的瞬時起動過程中,并不是所有的振動在共振發生后都存在拍振現象,主要的原因在于起動加速度和阻尼比的影響。通過理論分析與數值計算知:起動加速度大,轉子能夠快速通過共振區域[13],這樣共振幅值小,易形成明顯的拍振現象;起動加速度較小,轉子在通過共振區域時的振動幅值大,使得強迫振動和伴隨振動的幅值之差過大,難以形成拍振。阻尼比在一定程度上也對轉子在通過共振區域的振動產生影響,主要是共振區域延遲滯后了,阻尼比越大,遲滯現象越明顯,響應調節的時間延長,易形成拍振。因此,使用本文方法計算系統動力學參數時,拍振峰值點越多、越密集,計算結果就越精確。

4 實驗驗證

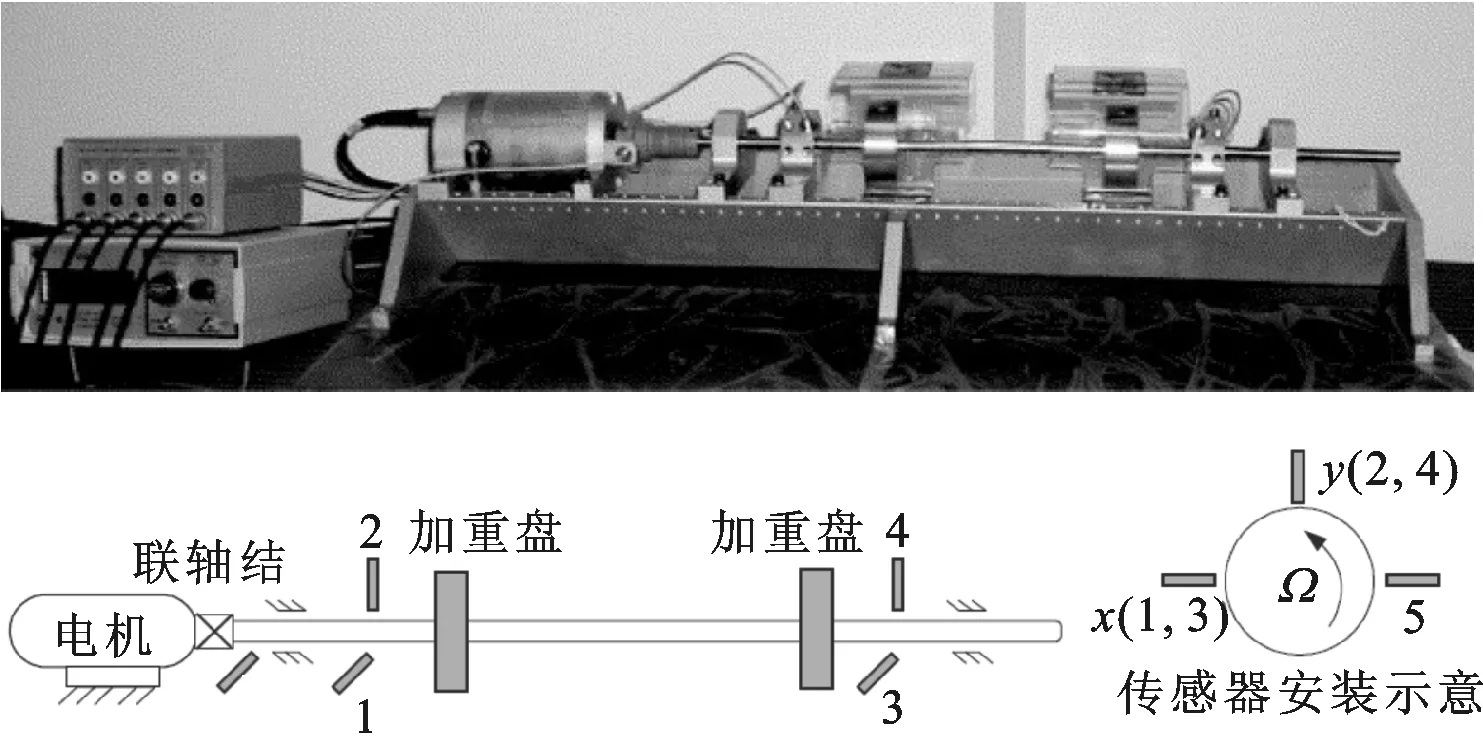
1～5:電渦流傳感器圖6 轉子實驗臺結構

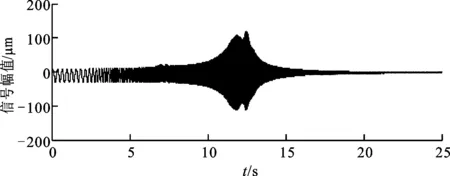
圖7 轉子起動過程實驗測試信號

實驗驗證所用的轉子實驗臺(圖6所示)為BentlyRotorkit-4。實驗中用4個電渦流傳感器分別測量轉子電機端、自由端水平和垂直方向上的振動位移信號,另外采用一個電渦流傳感器獲取轉子的鍵相信號。起動過程測試的電機端垂直方向的振動位移信號如圖7所示。起動過程中振動信號和鍵相信號采用SonyPC208AX數字磁帶記錄儀進行采樣和存儲,每通道信號的采樣頻率為24 000Hz。起動實驗從180r/min盤車轉速開始,并以一定的升速率提速直到轉速為4 000r/min止。起動過程各時刻點轉速通過測試到的鍵相信號進行計算,由此得到的起動過程瞬時轉頻如圖8所示。

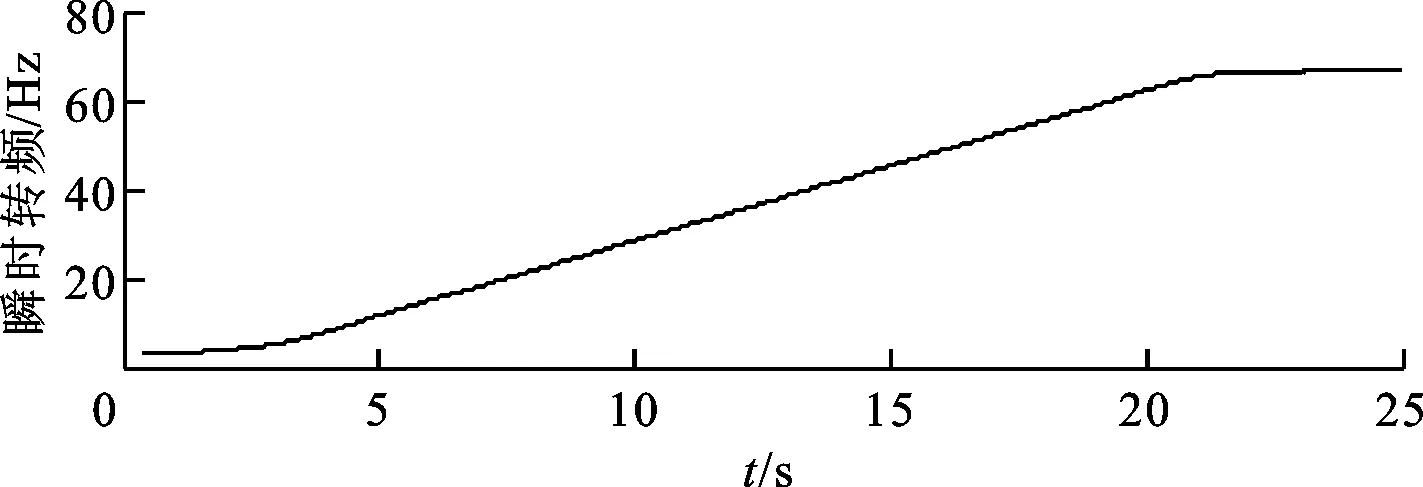
圖8 轉子起動過程的瞬時轉頻

根據測試到的振動響應,計算得到振動響應包絡信號的峰值點曲線和谷值點曲線如圖9所示。相鄰峰值點的準確時間分別為11.893 3s、12.482 9s,同時根據圖7和圖8確定出相鄰峰值點對應時刻的瞬時轉頻分別為35.826 89Hz、37.822 6Hz,對應的升速率為3.387 6Hz/s。根據式(9)可計算出ωd=220.724 6rad/s或fd=35.129 4Hz。

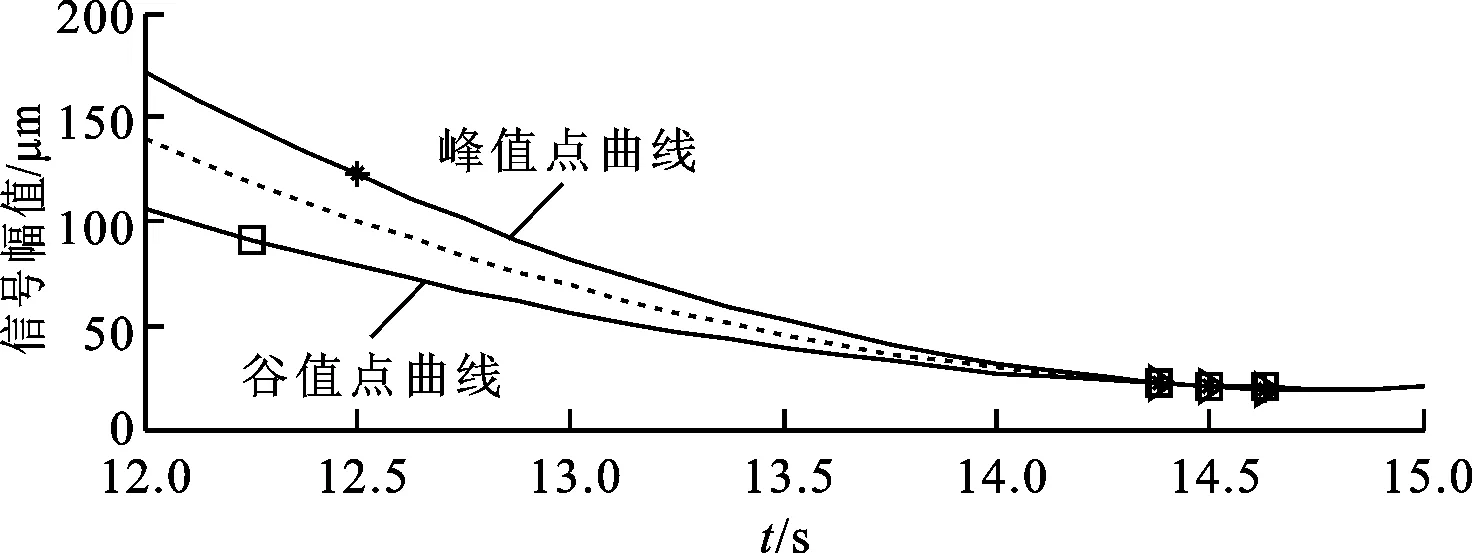
圖9 振動響應包絡信號的峰值和幅值

根據文獻[15-18]中的轉子響應的峰值滯后現象,對轉子系統以相同的升速率和降速率進行了幾次起停過程的振動響應實驗測試。計算得到的升速過程中響應峰值對應的頻率平均值為35.363 5Hz,計算得到的降速過程中響應峰值對應的頻率平均值為34.665 9Hz。根據轉子響應的峰值滯后現象,升速過程的峰值頻率實際是有阻尼的固有頻率的上限,降速過程的峰值頻率實際是有阻尼的固有頻率的下限,因此實際有阻尼的固有頻率可用這兩個上下限進行估計,估計結果為35.014 8Hz,該結果與本文的方法估計的結果相比,差值僅為0.114 6Hz。

根據峰值點曲線、谷值點曲線以及中間曲線計算自由伴隨振動的衰減曲線,再根據式(11)、利用矩陣最小二乘法估計的阻尼比和無阻尼固有頻率分別為0.003 1、ωn=220.725 7rad/s或fn=35.129 6Hz。

5 結 論

本文提出了一種基于起動過程瞬態振動響應的轉子動力學參數識別方法。在給出參數估計原理的基礎上,利用起動過程振動響應仿真信號和實驗測試信號對轉子系統的動力學參數進行了估計,估計結果驗證了本文方法的正確性、有效性和準確性。本文轉子參數識別方法僅利用轉子起動過程的振動響應信號,所有計算和識別均在時域內進行,計算量小、簡單方便。由于本文方法是基于起動過程振動響應信號中自由伴隨振動分量和強迫振動響應分量疊加形成的拍振現象,而起動過程振動響應信號出現拍振現象比較普遍,所以該方法具有廣闊的應用范圍。

[1] 黃文虎, 邵成勛. 振動系統參數識別的時域方法 [J]. 振動與沖擊, 1982(1): 43-53.HUANGWenhu,SHAOChengxun.Amethodforidentificationofvibrationparametersfromthetime-domain[J].JournalofVibrationandShock, 1982(1): 43-53.

[2] 黃文虎, 邵成勛, 劉華, 等. 近代振動系統參數識別技術的發展與展望 [J]. 應用力學學報, 1985, 2(3): 69-82, 100. HUANG Wenhu, SHAO Chengxun, LIU Hua, et al. The developments and predictions in modern parameter identification of vibrating system [J]. Journal of Applied Mechanics, 1985, 2(3): 69-82, 100.

[3] IBRAHIM S R. A time-domain modal vibration test technique [J]. The Shock and Vibration Bulletin, 1973, 43(4): 21-37.

[4] IBRAHIM S R. The experimental determination of vibration parameters from time responses [J]. The Shock and Vibration Bulletin, 1976, 46(5): 187-196.

[5] IBRAHIM S R. A method for direct identification of vibration parameters from the free response [J]. The Shock and Vibration Bulletin, 1977, 47(4): 183-198.

[6] SMITH W R. Least squares time domain method for simultaneous identification of vibration parameters from multiple free response records [C]∥AIAA/ASME/ASCE/AHS 22nd SDM Conference. Reno, NV, USA: AIAA, 1981: 194-201.

[7] IBRAHIM S R. The use of random decrement technique for identification of structural modes of vibration [J]. Journal of Spacecraft and Rockets, 1977, 14(11): 696-700.

[8] 周傳榮, 包益民, 徐慶華. 隨機減量、ITD及雙遞推等方法在飛機結構上的應用 [J]. 振動與動態測試, 1988(2): 13-19.

[9] 聶雪媛, 丁樺. 基于隨機減量技術的模態參數識別方法探討 [J]. 機械設計, 2012, 29(8): 1-4. NIE Xueyuan, DING Hua. Discussion on modal parameter identification method based on random decrement technique [J]. Journal of Machine Design, 2012, 29(8): 1-4.

[10]李慧, 周晶, 杜永峰, 等. 隨機子空間法參數識別與有限元分析 [J]. 低溫建筑技術, 2008, 125(5): 44-48. LI Hui, ZHOU Jing, DU Yongfeng, et al. Parameter identification and finite element analysis based on stochastic subspace method [J]. Low Temperature Architecture Technology, 2008, 125(5): 44-48.

[11]張笑華, 任偉新, 禹丹江. 結構模態參數識別的隨機子空間法 [J]. 福州大學學報(自然科學版), 2005, 33(增刊): 46-49. ZHANG Xiaohau, REN Weixin, YU Danjing. Structural modal parameter identification applying stochastic subspace identification [J]. Journal of Fuzhou University (Natural Science), 2005, 33(S): 46-49.

[12]倪振華. 振動力學 [M]. 西安: 西安交通大學出版社, 1989: 92-94.

[13]熊萬里, 聞邦椿, 段志善. 轉子系統瞬態過程的減幅特性及共振區遲滯特性 [J]. 振動與沖擊, 1999, 18(4): 12-15, 89. XIONG Wanli, WEN Bangchun, DUAN Zhishan. Characteristics of amplitude decreasing and resonance band delaying in transient processes of rotor systems [J]. Journal of Vibration and Shock, 1999, 18(4): 12-15, 89.

[14]朱向哲. 轉子-軸承系統起動過程瞬態不平衡響應的有限元分析 [J]. 石油礦場機械, 2007, 36(8): 14-17. ZHU Xiangzhe. Finite element analysis of transient imbalance response for a rotor-bearing system during start-up [J]. Oil Field Equipment, 2007, 36(8): 14-17.

[15]繆紅燕, 高金吉, 徐鴻. 轉子系統瞬態不平衡響應的有限元分析 [J]. 振動與沖擊, 2004, 23(3): 1-4, 20. MIAO Hongyan, GAO Jinji, XU Hong. Transient response of unbalanced rotor system through its critical speed [J]. Journal of Vibration and Shock, 2004, 23(3): 1-4, 20.

[16]袁惠群, 朱向哲, 李東, 等. 轉子系統瞬態熱起動過程動力學特性研究 [J]. 振動與沖擊, 2009, 28(7): 33-38. YUAN Huiqun, ZHU Xiangzhe, LI Dong, et al. Dynamic characteristics of transient starting up of a rotor system [J]. Journal of Vibration and Shock, 2009, 28(7): 33-38.

[17]肖明杰, 黃金平, 李鋒. 基于傳遞矩陣法的渦輪泵轉子系統瞬態動力學特性預測和分析 [J]. 機械強度, 2011, 33(6): 900-906. XIAO Mingjie, HUANG Jinping, LI Feng. Prediction and analysis to the transient dynamic characteristics of the turbo-pump rotor system based on the transfer matrix method [J]. Journal of Mechanical Strength, 2011, 33(6): 900-906.

[18]黃金平, 任興民, 張萌. 單盤柔性轉子瞬態平衡 [J]. 機械科學與技術, 2006, 125(2): 238-241. HUANG Jinping, REN Xingmin, ZHAO Meng. Transient balance of flexible rotors with one disc [J]. Mechanical Science and Technology, 2006, 125(2): 238-241.

[本刊相關文獻鏈接]

夏凱,孫巖樺,洪德江,等.軸向拉緊的圓弧端齒軸段扭轉特性研究.2016,50(5):51-56.[doi:10.7652/xjtuxb201605008]

章云,梅雪松.機床柔性主軸轉子低速無試重動平衡方法研究.2016,50(4):89-93.[doi:10.7652/xjtuxb201604014]

李志剛,李軍,豐鎮平.進口防旋板對孔型密封非定常氣流激振特性的影響.2016,50(1):16-21.[doi:10.7652/xjtuxb 201601003]

張俊紅,馬梁,魯鑫,等.機動飛行下擠壓油膜阻尼器對碰摩故障轉子系統的影響.2015,49(11):62-70.[doi:10.7652/xjtuxb201511011]

楊琴,劉宇陸,張海軍,等.氣體稀薄效應對微機電系統(MEMS)氣體軸承-轉子系統不平衡響應的影響.2015,49(7):134-139.[doi:10.7652/xjtuxb201507022]

(編輯 苗凌)

Method for Recognizing Kinetic Parameters of Rotor by Transient Vibration Response During Starting Process

ZHANG Xining,WU Jili,WANG Ben

(State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

Analyzing the compositions of the vibration response signals of rotor system during starting process and the cause of beat vibration phenomenon in vibration response signal, one transient vibration response of starting process based identification method for rotor kinetic parameters in time domain is proposed. Here unbalanced vibration response signal during starting process is considered to identify the natural frequency and damping parameters of rotor system instead of sine sweep vibration response signal in frequency domain parameter identification method. The rule of parameter estimation is given and the first-order natural frequencies and ratios of damping of rotor systems is estimated by both simulated and experimental response signals during starting process. The proposed method for parameter identification only needs the vibration response signals of rotor during the starting process in time domain, so complex exciting equipment is unnecessary.

rotor; starting process; vibration response; beat vibration; kinetic parameter

2015-11-29。 作者簡介:張西寧(1965—),男,教授,博士生導師。 基金項目:國家自然科學基金資助項目(51275379);國家自然科學基金優秀創新群體資助項目(51421004)。

時間:2016-05-10

10.7652/xjtuxb201607001

TB123

A

0253-987X(2016)07-0001-06

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160510.1524.016.html