BPSK信號在Nakagami衰落信道下誤碼性能分析

孫蔓，徐榮蓉，孫得娣，張佩佩

BPSK信號在Nakagami衰落信道下誤碼性能分析

孫蔓，徐榮蓉，孫得娣，張佩佩

首先介紹了BPSK信號調制與解調的基本原理以及Nakagami衰落信道的統計特性；隨后重點分析、推導了BPSK信號在通過Nakagami衰落信道后，經相干解調的平均誤碼率理論閉型表達式；最后在Matlab仿真平臺中對該誤碼率閉型表達式進行了仿真驗證，并總結了BPSK調制在Nakagami衰落信道中的誤碼性能。

BPSK；Nakagami信道；Matlab仿真；誤碼率

0 引言

在實際的通信信道中，大多數信道具有帶通傳輸特性，而數字基帶信號不能直接在這種帶通傳輸特性的信道中傳輸。所以，必須用數字基帶信號對載波進行調制。與模擬通信系統相比，數字調制和解調同樣是通過某種方式，將基帶信號的頻譜由一個頻率位置搬移到另一個頻率位置上去。而數字調制的基帶信號不是模擬信號而是數字信號，數字調制是利用數字信號的離散值去鍵控載波。用數字基帶信號改變正弦載波的幅度、頻率或相位中的某個參數而產生相應的數字振幅調制、數字頻率調制和數字相位調制。因此，在二進制數字調制中，當正弦載波的相位隨二進制數字基帶信號離散變化時則產生二進制移相鍵控信號，即BPSK信號。通過研究BPSK信號在Nakagami衰落信道下的誤碼率，從而得到衰落信號統計的特性對系統性能分析提供相應的依據。

1 BPSK信號的數學原理

1.1 BPSK信號調制原理

在數字信號經通信信道傳輸時，由于調制器是接口器件，其將數字信息映射成與信道特性相匹配的模擬波形。一般先從信息序列｛an｝一次提取k=log2M個二進制數字形成分組，再從M=2k個確定的有限能量波形｛sm（t）, m=1,2,...,M｝中選擇其中之一送往信道進行傳輸。當序列｛an｝到波形｛sm（t）｝的映射沒有受到先前發送波形的約束時，這種調制器稱為無記憶的；而在任意時間間隔發送的波形決定于一個或多個先前發送波形的約束時，這種調制器就稱為有記憶的。在數字通信系統中，調制器將二進制數字序列映射成一組相應的信號波形，這些波形的差別在于幅度、相位、頻率或者兩個或多個信號參數的組合。其中，數字相位調制通常被稱為相移鍵控(PSK)。在采用無記憶調制方式的情況下，假定在調制器輸入端的二進制數字序列的速度均為Rb/s，那么在數字相位調制中，M個信號波形[2]可表示為公式（1）：

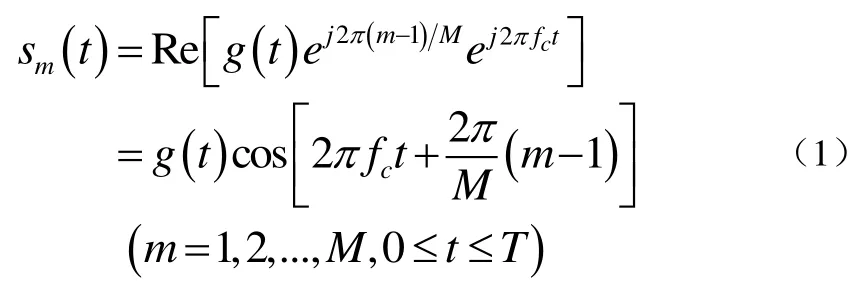
上式中，g（t）是信號脈沖波形，其形狀影響發送信號的譜；而θm=2π（m-1）M是載波的M個可能的相位用于傳送發送信息；時間間隔T=k R稱為符號間隔。這些信號波形具有相等的能量，即公式（2）：

其中，εg表示脈沖g（t）的能量。

該M個信號波形可以表示為具有單位能量的兩個標準正交信號波形f1（t）和f2（t）的線性組合，即式（3）：

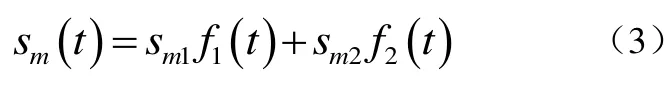
當M=2,4,8時該信號分別表示為 BPSK、QPSK和8PSK。并且當M=2時，其相當于一維信號，與二進制數字脈沖幅度調制(PAM)信號相同。其中，數字PAM信號波形一般表示為式（5）：

其中，Am表示M個可能的幅度，相應于M=2k個可能的k比特組或符號。信號幅度Am取離散值（電平）為式（6）：

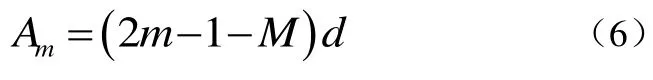
上式中，d是相鄰信號幅度之間的距離。所以在M=2的情況下，二進制PAM波形具有特殊性質，即式（7）：

所以，該兩個信號具有相等的能量且互相關系數為-1，其被稱為雙極性信號。

1.2 BPSK信號解調原理

在發送端的調制器將數字序列映射成信號波形后通過信道傳輸時，該信號會受到信道高斯噪聲相加的影響。假定信道以加性高斯白噪聲(AWGN)來惡化信號，那么在0≤t≤T間隔內，接收信號可以表示為式（8）：

其中，n（t） 表示具有功率密度譜Φ（f）=N02（W/Hz）的加性高斯白噪聲的樣本函數。通過對r（t）在信號間隔時間上經過接收機使錯誤概率最小使系統達到最佳。一般可將接收機分為兩個部分即信號解調和檢測器，如圖1所示：

圖1 BPSK信號解調原理圖

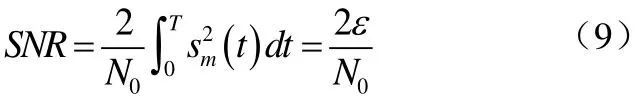
上式表明匹配濾波器的輸出信噪比決定于信號波形sm（t）的能量。

對于BPSK信號在AWGN信道下在進行無記憶調制時，基于最大似然準則（ML）的判決規則進行判決，該二進制雙極性信號的平均錯誤概率[2]是式（10）：

其中，ε/N0稱為比特信噪比。

2 Nakagami衰落統計特性

在移動無線信道中，瑞利分布和萊斯分布都能很好的對信號通過衰落信道后的包絡進行建模。但是，在實際的無線環境中，Nakagami分布能夠與測試結果更加匹配吻合[3]。在Nakagami衰落信道下，系統傳輸的符號的包絡受到的衰落幅度α服從Nakagami分布即m分布，其概率密度函數為式（11）：

其中，m和ω是Nakagami分布的兩個重要參數，表達式為式（12）：

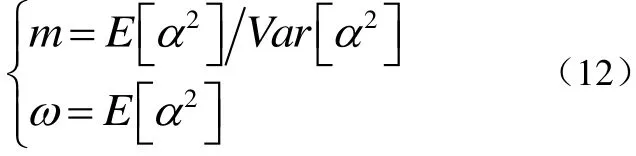
其中，E［·］表示求均值，Var［·］表示方差。ω是衰落幅度α的均方值，m被稱為形狀因子或衰落指數，表示此時小尺度衰落的嚴重程度，其取值滿足m≥1/2。Γ（·）表示伽馬函數并定義為式（13）：

其中，對衰落指數m的不同取值存在幾種特殊情況。

為了進行統一對比，所有曲線對應的ω取值都為1，如圖2所示：

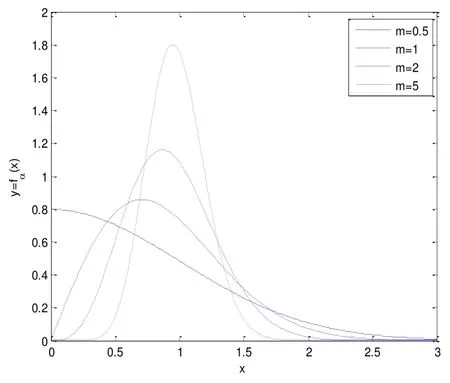
圖2 Nakagami分布的概率密度函數曲線圖

從圖中可以看出，m取值越大，概率密度函數曲線越陡峭，即對應的方差越小，衰落越輕微。當m取值趨向于無窮大時，其概率密度函數演變為Dirac沖擊函數，此時以概率1取得均值，方差為0，信道中不存在小尺度衰落。綜上所述，當衰落參數m的取值變化時，Nakagami衰落信道的衰落嚴重程度也會隨之變化。并且當m取特定數值時，Nakagami衰落信道模型能夠有效地涵蓋現有的經典衰落信道模型，具有很強的通用性。

根據文獻[4]假設Nakagami衰落信道當中存在加性高斯白噪聲，其功率譜密度為N0，發送端發送功率為E，接收端瞬時接收信噪比記為γ，每個符號對應的平均接收信噪比記作，則兩者表達式分別為式（14）：

通過單個符號的瞬時接收信噪比γ的概率密度函數和單個符號包絡受到的衰落幅度α的概率密度函數的兩者關系可得在Nakagami衰落信道下，接收端接收到單個符號的信噪比γ的概率密度函數表達式為式（15）：

3 BPSK在Nakagami衰落信道下理論平均誤碼率推導

BPSK信號序列產生之后，其會被傳送到信道中。而實際的信道是一個充滿各種干擾的環境，所以調制后的信號不可能在信道中不受干擾影響的直接進行傳輸。一般的信道干擾包括乘性干擾和加性干擾，其中乘性干擾是伴隨信號的存在而存在、消失而消失的，加性干擾是不管有沒有傳送信號始終存在信道所固有的干擾。所以 BPSK信號在經過Nakagami信道時受到乘性干擾，同時為更加逼真的去模擬這樣的調制信號的傳輸環境，所以在經過該衰落的序列中隨機疊加不同信噪比的高斯白噪聲。

由于頻率非選擇性信道會導致發送信號的乘性失真，信道慢衰落的條件要求至少在一個信號傳輸間隔內將乘法過程看做是一個常數。所以假設信道衰落足夠慢以致相移是能夠從接收信號中無誤差的被估計出，這種情況便能夠實現接收信號的理想的相干檢測。對BPSK采用一個匹配濾波器處理接收信號，通過計算判決變量并依據其確定差錯率確定該通信系統的性能。根據前面所述BPSK信號的解調原理可知對于某一固定衰減α，其接收端接收到的單個符號的信噪比γ函數的BPSK差錯率為式（16）：

上式中，γ=α2ε/N；Q（·）是一種經常用來表示高斯

0 PDF尾部曲線下的面積的函數，定義為式（17）：

上式的 BPSK差錯率是在條件衰減α固定不變的情況下得出的。所以為了得到隨衰減α隨機變化時的差錯率，可將Pγ（γ）對變量γ的概率密度函數求平均，即計算如下的積分式（18）：

其中，pγ（γ）是衰減α隨機變化時信噪比γ的概率密度函數。所以BPSK在Nakagami衰落信道下誤碼率的計算表達式為式（19）：

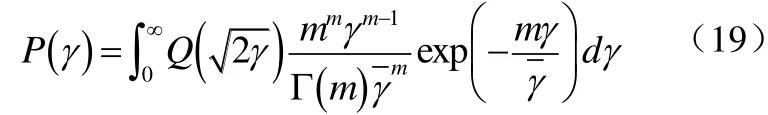
其中，Q（·）還可以寫成另一種表達形式[4]即式（20）：

所以，將公式（20）運用到公式（19）中可得式（21）：

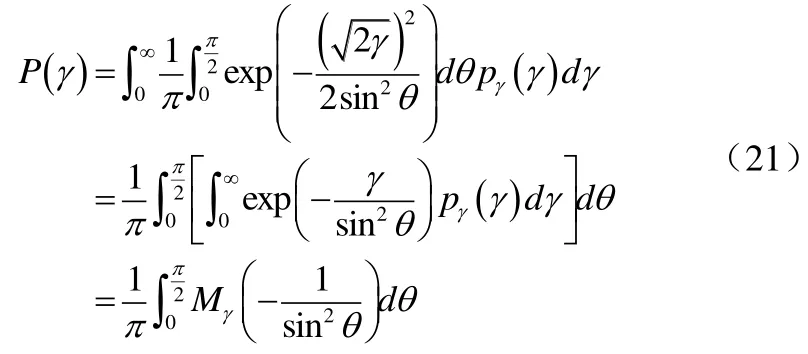
在公式（21）的推導中，用到了矩生成函數（MGF，The moment generating function）。其定義為式（22）：

對于Nakagami衰落信道的接收端接收到單個符號的信噪比γ的概率密度函數而言，其矩生成函數可以化簡[4]寫成式（23）：

根據公式（23），公式（21）可以化為式（24）：

其中，2F1（·,·;·;·）為Gauss hyper-geometric函數[5]，其定義為式（26）：

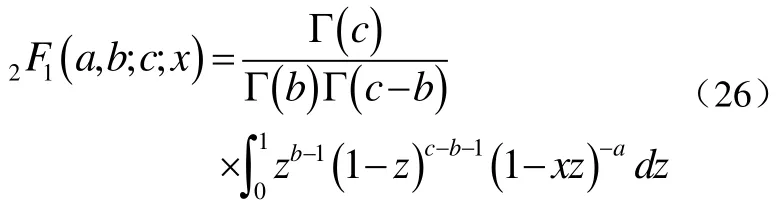
通過進行上述系列的數學的變量代換和變形便可得到BPSK信號在經過Nakagami衰落信道后的誤碼率的一個閉合式的解。相較于原來的無窮積分表達式，該閉合式不僅更好的反映了誤碼率同接收信噪比和衰落指數的關系而且有利于計算和分析，使得仿真更加方便精確。

由于上式所得誤碼率是對一般的衰落指數m≥1/2適用的，而當m無限趨近于無窮大時，依據Nakagami信道在接收端接收到的單個符號信噪比的概率密γ度表達式可知其成為了Dirac沖擊函數即接收到的信噪比γ以無限大的概率出現在均值點沒有衰落，相當于Nakagami衰落信道對信號所產生的乘性干擾為 1即其是一個無衰落的信道。所以此時BPSK信號在經過Nakagami信道后，接收端接收到的信號實際上等效為一個疊加了高斯白噪聲的原始的發送信號。根據 BPSK信號在通過具有高斯白噪聲的信道后其接收到的信號的概率密度函數和判決法則等可得m→∞時，BPSK信號的誤碼率[1]的表達式為式（27）：

其中，erfc（·）為高斯誤差函數[6]，其定義為式（28）：

4 仿真及結果分析

基于前面的數學原理，利用MATALB進行仿真并分析數學理想模型建立的合理性。根據BPSK信號在Nakagami衰落信道下誤碼率的計算表達式可知該信號的誤碼率不僅與Nakagami分布的衰減指數m有關，還與其每個符號對應的平均接收信噪比γ有關。對于不同的衰減指數m賦予不同的數值即做不同的變化，同時對該信道中的平均信噪比從0db到40db不斷地進行變化，這樣便可得到在不同的衰減指數m和平均信噪比γ情況下的BPSK信號的誤碼率。并且對原始信號的誤碼率取對數得到誤碼率與衰減指數m和平均信噪比的關系的仿真圖如圖3所示：

圖3 BPSK在Nakagami衰落信道下誤碼率的理論仿真圖

從而便于分析BPSK信號在經過Nakagami衰落信道后的系統性能。

圖中藍色實線描繪的是通過超幾何函數公式（25）和誤差函數公式（27）所表示的BPSK誤碼率的理論計算值；而紅色原點和方塊所描繪的則是通過無窮積分公式（19）所表示的BPSK誤碼率的基準理論仿真值。這兩類曲線的良好重合性證明了本文所推導得到的Nakagami衰落信道下BPSK理論平均誤碼率公式的正確性。從上述的BPSK誤碼率的仿真圖可以看出，BPSK信號m的誤碼率與平均信噪比及衰落指數息息相關：當衰落指數m為一固定值時，接收的平均信噪比越大，BPSK信號的誤碼率越低；而當平均信噪比為一固定值m時，BPSK信號的誤碼率隨著Nakagami信道的衰落指數m的增大而減小，即m越大時誤碼m率越小。所以當m逐漸增大時，系統性能將得到改善，當m為無窮時，系統性能趨于無衰落的高斯信道。

6 總結

本文在簡要介紹了 BPSK信號的調制與解調原理和Nakagami衰落信道的統計特性后，推導了Nakagmi衰落信道下，BPSK經相干解調和最大似然判決輸出的統計平均誤碼率理論閉型表達式，并進行了計算機仿真驗證。仿真顯示，BPSK信號的誤碼率與Nakagami衰落信道的衰落指數和接收端每個符號的平均信噪比有關，通過合理的選擇這兩個參數可使得誤碼率最低、系統性能達到最好。

[1] 樊昌信.通信原理(第六版)[M].北京：國防工業出版社, 2008.

[2] John G.Proakis著,張力軍等譯.數字通信(第四版)[M].北京電子工業出版社, 2003,1.

[3] Nakagami M. The m-distribution: A general formula of intensity distribution of rapid fading[J].Statistical Method of Radio Propagation,1960.

[4] M.K. Simon and M.-S. Alouini. Digital communication over fading channels,2nd ed.[M].New York:Wiley,2005.

[5] A. Erdelyi. Higher Transcendental Functions[M]. New York: McGraw-Hill.1953.Vol.1.

[6] S.Gradshteyn, I.M.Ryzhik. Table of Integrals. Series and products(7th ed.)[M].San Diego: Academic Press,2007.

Analysis of BER Performance of BPSK Modulation over Nakagami Fading Channel

Sun Man, Xu Rongrong, Sun Dedi, Zhang Peipei
(College of Computer and Information, Hohai University, Nanjing 211100,China)

This paper firstly introduces the basic principls of BPSK signal modulation and demodulation, and the statistical characteristics of Nakagami fading channel. Then it focuses on the analysis and derivation of the BPSK signal in the Nakagami fading channel through the coherent demodulation of the average error rate theoretical closed form expression. Finally, the error rate closed form expression is simulated in the Matlab simulation platform, and the BER performance of BPSK modulation in Nakagami fading channel is summarized.

BPSK; Nakagami Channel; Matlab Simulation; BER

TP393

A

1007-757X(2016)09-0071-04

2016.01.15）

孫 蔓（1995-），女，河海大學，計算機與信息學院，碩士研究生，研究方向：MIMO系統及多天線技術，南京 211100徐榮蓉（1992-），女，河海大學，計算機與信息學院，碩士研究生，研究方向：現代無線通信系統，南京 211100孫得娣（1992-），女，河海大學，計算機與信息學院，碩士研究生，研究方向：無線通信網絡與MIMO系統，南京 211100張佩佩（1992-），女，河海大學，計算機與信息學院，碩士研究生，研究方向：新一代MIMO無線通信系統，南京 211100