寬帶匹配網(wǎng)絡中參量法與蓋維茨法的數(shù)值誤差研究

郭世樺，閻敬業(yè)，吳 季

（1.中國科學院微波遙感技術重點實驗室 北京 100190；2.中國科學院國家空間科學中心 北京100190；3.中國科學院大學 北京100190）

寬帶匹配網(wǎng)絡中參量法與蓋維茨法的數(shù)值誤差研究

郭世樺1，2，3，閻敬業(yè)1，2，吳 季2

（1.中國科學院微波遙感技術重點實驗室 北京 100190；2.中國科學院國家空間科學中心 北京100190；3.中國科學院大學 北京100190）

在寬帶電路以及寬帶天線設計中經(jīng)常需要設計寬帶匹配網(wǎng)絡，傳統(tǒng)解析方法只針對簡單負載有效。與解析方法不同，數(shù)值方法可以在知道負載實頻數(shù)據(jù)的條件下進行寬帶化設計。本文對數(shù)值方法中常用的參量法與蓋維茨法來構成最小函數(shù)的問題進行了理論分析與數(shù)值編程，比較了兩者在生成最小阻抗函數(shù)上的誤差大小，且分析了兩者產(chǎn)生誤差的原因。結果表明，對于階數(shù)比較低的情況，采用參量法和蓋維茨法均可行且兩者誤差幾乎相等；但是對于階數(shù)比較高的情況，參量法比蓋維茨法的數(shù)值誤差小幾個數(shù)量級，這對于設計寬帶匹配網(wǎng)絡具有很大的指導意義。

寬帶匹配網(wǎng)絡；參量法；蓋維茨法；網(wǎng)絡分析與綜合

在電路設計以及天線設計中，常常遇到寬帶匹配的問題，比如寬頻帶低噪聲放大器的設計，寬帶功放的設計以及寬帶天線的匹配網(wǎng)絡等。這些問題均是在知道負載對應若干個頻點的輸入阻抗情況下，去設計寬帶匹配網(wǎng)絡的問題。在傳統(tǒng)的解析法[1-4]中只有對于簡單的負載才能有解析的公式。而在現(xiàn)代通信中，通過測量得到的負載數(shù)據(jù)更具有現(xiàn)實意思，從而也產(chǎn)生了各種各樣的數(shù)值解法以及CAD程序來設計寬帶匹配網(wǎng)絡。1977年，H.J.Carlin[5]提出的實頻技術法[6-9]就是一種很有效的CAD方法，以及用于雙匹配問題的直接計算法[10-11]等。在這些數(shù)值算法中，都涉及到由偶部多項式構成最小函數(shù)的問題。在這個問題中，主要有參量法以及蓋維茨法，但是在應用這兩種方法時，大家對兩者方法的數(shù)值誤差沒有進行深入的研究，以及對兩種方法的使用范圍沒有很清晰的認識。文中在充分分析兩種方法的基礎上，總結了兩種方法的實現(xiàn)步驟，并且通過兩個具體的例子比較了兩種方法的數(shù)值誤差，且分析了兩者誤差的原因，最后給出了在設計寬帶匹配網(wǎng)絡中的一些結論。

1 參量法

在寬帶匹配網(wǎng)絡設計的過程中，一個主要的難題就是根據(jù)預定的系統(tǒng)性能來構成一個合適的正實函數(shù)，而這可以通過最小函數(shù)來實現(xiàn)，最小函數(shù)的極點必須在s域的左半平面，相應的留數(shù)為正，即函數(shù)可以寫成博德形式或者參量法[12-15]表示成如下形式

如果滿足以下條件:（a）極點s=sj在左半平面；（b）常數(shù)F0非負；（c）F（s）的偶部非負。則該函數(shù)為正實函數(shù)。通過（1）式可以構成一個最小電抗函數(shù)Z（s）=R（s2）+odd（Z）或者最小電納函數(shù)Y（s）=G（s2）+odd（Y）。如果偶部R（s2）或者G（s2）已知，則可以很容易的構成一個正實函數(shù)。

最小導抗函數(shù)的實部可以寫成如下的全極點形式，且為偶多項式

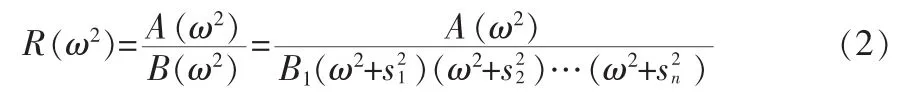
其中{s1，s2，…sn}是多項式F（s）的左半平面的極點，且

在s域，則有

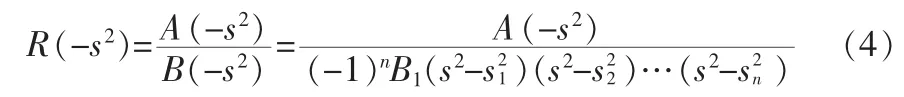
另外，有

2 蓋維茨法

與參量法不同，蓋維茨法[16]是通過把偶部R（-s2）寫成有理函數(shù)的形式，再通過希爾伯特變換得到虛部，這在數(shù)值計算上有很大的優(yōu)勢。

假設最小函數(shù)F（s）可以寫成如下形式

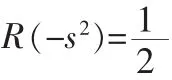
R（-s2）可以寫成如下兩種形式

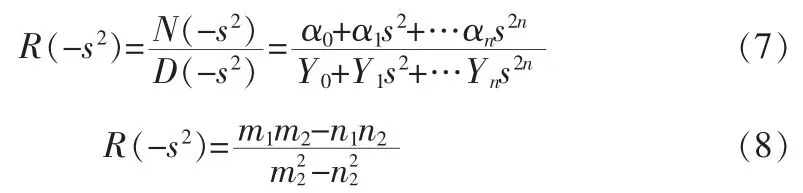
從（7）（8）兩式可以得出

其中y（s）包含了Y（s）所有左半平面的極點，y（-s）包含了所有右半平面的極點。

求出了極點很容易構建出y（s），即

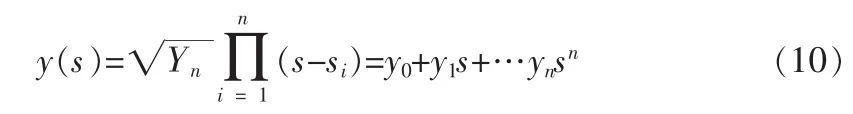
只要求出了yi，則可以由（8）（9）求出xi，易知α0=x0y0

由式（10）（12）求出了y（s）和x（s），就可以得到最小函數(shù)F（s）。

3 數(shù)值誤差比較及分析

上面兩小節(jié)對參量法和蓋維茨法生成最小函數(shù)的方法進行了詳細的分析，且給出了具體的步驟。基于前兩節(jié)的分析，我們假設偶部表示成R（ω2）=A（ω2）/B（ω2）的形式。由給出的偶部，采用參量法以及蓋維茨法來編程分別計算兩者的誤差大小。設由參量法求出的最小函數(shù)為Zpara=apara/bpara，由蓋維茨法求出的最小函數(shù)為Zgewe=agewe/bgewe，則由Zpara及Zgewe可以再次計算出偶部的表達式 Rpara=Apara/Bpara和Rgewe=Agewe/Bgewe， 則兩者的計算誤差由下兩式（13）（14）給出，具體流程圖如圖1所示

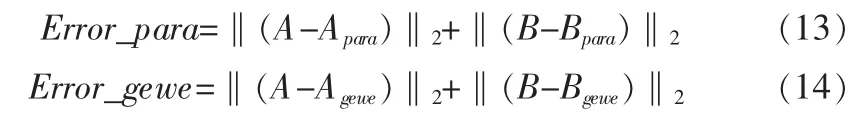
圖1 數(shù)值實驗流程圖

下面通過兩個例子來比較參量法與蓋維茨法在構成最小函數(shù)F（s）=a（s）/d（s）時的誤差大小。

例1：給出偶部的分子和分母分別為A=[1 2 3 4 5]，B=[5 4 3 2 1]，編程計算結果如表1。

表1 階數(shù)低時的實驗結果

由表1的結果，根據(jù)式（13）（14）可以算出兩者的數(shù)值誤差如下

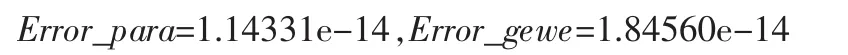
例2：給出偶部的分子和分母分別為A=[1 2 3 4 5 6 7 8 9 10 11 12 3 14 15 16 17 18 19 20]，B=[20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1]，編程計算結果如表2、表3及表4。

同樣可以利用式（13）（14）計算兩者的數(shù)值誤差，計算結果如下

Error_para=1.0833e-06，Error_gewe=3.7000e-03

從以上兩個例子可以看出在，如表1，當階數(shù)比較小（n＜5）時，參量法與蓋維茨法計算出來的誤差都在同一數(shù)量級，當然對于不同的計算機，由于計算機硬件資源不同，計算機的運算速度也不同，計算結果可能有些偏差，但是計算結果的數(shù)量級是一樣的。表2至表4則表明，當階數(shù)比較高時，可以看出參量法得出的計算結果明顯優(yōu)于蓋維茨法，誤差小了近（3.7000e-03）/（1.0833e-6）=3415倍。

通過一二節(jié)的理論分析，參量法是通過計算極點和留數(shù)來生成最小函數(shù)，先求出左半平面的極點，再進行式（10）運算而產(chǎn)生誤差。蓋維茨法的分母多項式產(chǎn)生方法與參量法類似，但分子多項式的計算過程中要進行式（12）矩陣求逆的運算，尤其是在遇到接近奇異矩陣時誤差更大。所以在進行寬帶匹配網(wǎng)絡的設計過程中，對于階數(shù)比較低的情況，采用參量法和蓋維茨法都是可以的，兩者誤差幾乎可以忽略；但是對于階數(shù)比較高的情況，參量法比蓋維茨法的數(shù)值誤差明顯小很多，具有幾個數(shù)量級的差別。這在設計寬帶匹配網(wǎng)絡的過程中對于不同階數(shù)的匹配網(wǎng)絡，需要采用不同的數(shù)值方法進行網(wǎng)絡的綜合，以使得誤差最小。

表2 階數(shù)高時的實驗結果一

表3 階數(shù)高時的實驗結果二

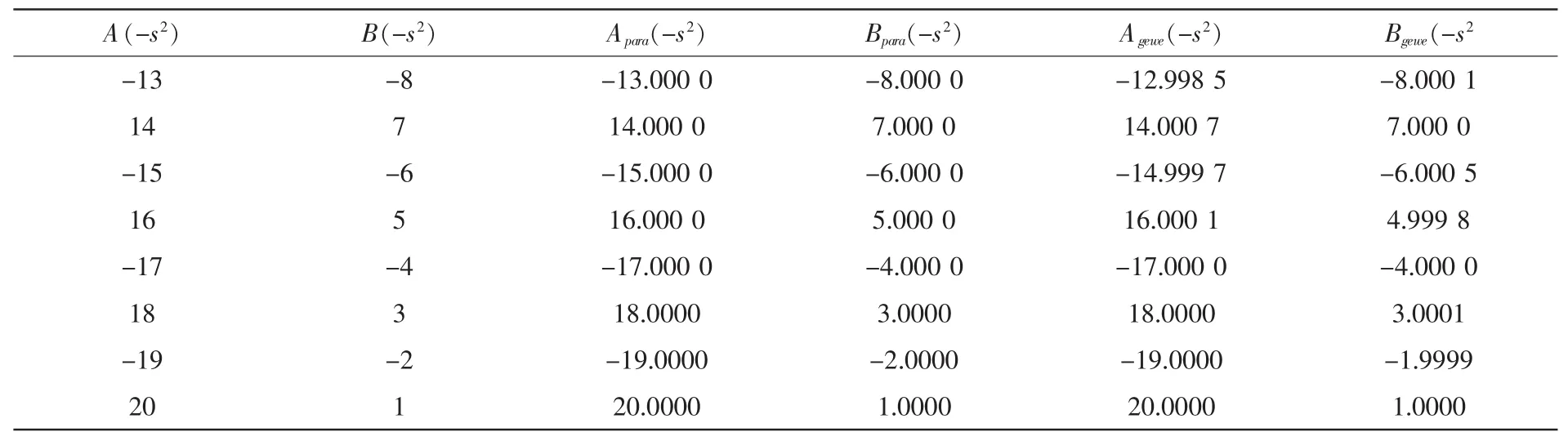
表4 階數(shù)高時的實驗結果三

4 結 論

在設計寬帶匹配網(wǎng)絡的方法中，數(shù)值法具有比解析法更廣的適用范圍。針對數(shù)值法在使用多項式偶部來構造最小函數(shù)的兩種方法，本文對參量法和蓋維茨法兩種方法構成最小函數(shù)的主要步驟進行了詳細的分析與總結，并編制了相應的程序進行了數(shù)值實驗。分析結果表明，對于不同階數(shù)、不同復雜度的匹配問題，兩種方法的誤差也不同，對于階數(shù)比較低的情況，采用參量法和蓋維茨法均可行且兩者誤差幾乎可以忽略；但是對于階數(shù)比較高的情況，參量法比蓋維茨法的數(shù)值誤差明顯小很多。最后分析了兩種方法產(chǎn)生誤差的原因，這對于設計寬帶匹配網(wǎng)絡具有指導意義。

[1]Fano R M.Theoretical limitations on the broadband matching of arbitary impedences[J].Frankin Inst.，1950（249）：57-83.

[2]Kuh E S，Patterson J D.Design theory of optium negative resistance amplifiers[J].Proc.IRE，1961，49（6）：1043-1050.

[3]Youla D C.A new theory of broadband matching[J].IEEE Trans.Circuit Theory，1964（11）：30-50.

[4]Chien W K.A Theory of broadband matching of a frequency dependent generator and load[J].Franklin Inst，1974（298）：181-221.

[5]Carlin H J.A new approach to Gain-Bandwidth problems[J]. IEEE transactions on circuits ans systems，1977（4）:170-175.

[6]陳軼鴻.寬帶天線阻抗匹配設計中的實頻法[J].電子學報，1997（3）：19-24.

[7]Carlin H J，Komiak J J.Anew method of broadband equalization applied to microwave amplifiers[J].IEEE Trans.Microw. Theory Tech.，1979（27）：93-99.

[8]Carlin H J，Amstutz P.On optimum broadband matching[J]. IEEE Trans.Circuits Syst，1981（28）：401-405.

[9]Yarman B S.Real frequency broadband matching using linear programing[J].RCA Review，1982（43）：626-654.

[10]Carlin H J，Yarman B S.The double matching problem:Analytic and Real frequency solution[J].IEEE transactions on circuits ans systems，1983（30）：15-28.

[11]Yarman B S.Broadband matching a complex generator to a complex load[D].PhD thesis，Cornell University，1982

[12]Bode H W.Network analysis and Feedback Amplifier Design [M].Van Nosrtand，1945.

[13]Fettweis A.Parametric representation of bruce functions，Int [J].Circuit Theory and Appl，1979（7）：113-119.

[14]Pandel J，F(xiàn)ettweis A.Broadband matching using parametric representations，IEEE Int，symp.on Circuit and System，1985（41）：143-149.

[15]Yarman B S，F(xiàn)ettweis A.Computer Aided Double Matching via Parametric Represantation of Brune Function[J].IEEE Trans.on CAS，1990，37（2）：212-222.

[16]Gewertz C.Synthesis of a Finite Four Terminal Network from its prescribed Driving Point Functions and Transfer Function[J].Journal of Mathematics and Physics，1932（12）：1-257.

Numerical error study on parametric approach and Gewertz procedure in designing broadband matching network

GUO Shi-hua1，2，3，YAN Jing-ye1，2，WU Ji2
（1.Key Laboratory of Micrwave Remote Sensing，Chinese Academy of Science，Beijing 100190，China；2.National Space Science Centre，Chinese Academy of Science，Beijing 100190，China；3.University of Chinese Academy of Science，Beijing 100190，China）

In broadband circuits design and broadband antenna design，there often occurs problem like designing a broadband matching network.There are usually two methods，traditional analysis method and numerical method.For analysis method，it is only apply for simple load effectively.However，we always need to design a broadband networks under the condition that we have several impedence values at some specfic frequency，numerical method can easy deal with it.In numerical method，there is a need to generate a minimal function based on the odd part，parameter approach and Gewertz procedure are usually used. In this paper，we carry on the theoretical analysis and numerical programming，the error between those two methods are compared，and causes of the error are also analyzed.Results show that in the case of low order，two methods are both feasible and almost equal error.But in the case of high order，the error caused by parametric approach is several orders of magnitude smaller than Gewertz procedure.This result has great guiding significance in designing broadband matching network.

broadband matching network；parametric approach；Gewertz procedure；network analysis and synthesism

TN711

A

1674－6236（2016）24-0119-03

2015-12-02 稿件編號：201512015

郭世樺（1990—），男，江西吉安人，碩士研究生。研究方向：寬帶天線設計、微波電路設計。