直立式防波堤迎浪面波壓力計算研究?

于龍基， 董 勝??， 段成林, 張華昌

(1.中國海洋大學工程學院, 山東 青島 266100；2.海軍工程設計研究院，山東 青島 266100)

?

直立式防波堤迎浪面波壓力計算研究?

于龍基1， 董 勝1??， 段成林1, 張華昌2

(1.中國海洋大學工程學院, 山東 青島 266100；2.海軍工程設計研究院，山東 青島 266100)

以Navier-Stokes方程為控制方程，使用VOF方法追蹤自由液面，由連續性方程和動量方程推導出源函數。基于非線性波浪理論和UDF對FLUENT進行二次開發，在數值水槽的各個功能區將不同的源項添加到動量方程中，實現動量源造波和消波的功能。此法可以有效地消除波浪在水槽出流邊界的反射及波浪遇到結構物后在入射邊界形成的二次反射，從而得到穩定的波動場。本文將這種方法應用于直墻防波堤上波浪壓力的數值模擬，分析了造波和消波的有效性，對直立式防波堤波浪力進行了數值研究。為了得到更精確的結果，采用結構化網格和非結構化網格相結合，在直墻防波堤附近使用三角形網格，在其他區域使用四邊形結構化網格，為了較好地捕捉自由液面，在液面上下一個波高的范圍內對網格進行加密。將計算結果與二階stokes波理論解進行對比，該方法計算結果與理論解一致，表明該方法能夠產生歷時較長的穩定的非線性規則波浪，能夠很好地吸收波浪遇到建筑物產生的反射波，可以有效消除建筑物反射波的影響，為實際工程方案的設計提供參考，有較高的實用價值。通過計算得到極端高水位，設計高水位，設計低水位時候的各個測點的最大正向波壓力和最大負向波壓力，并將計算結果與物理模型試驗數據和經驗公式結果進行對比，結果吻合較好。并且由于該數值方法可以考慮防波堤迎浪面不同傾角的工況，其適應范圍比經驗公式范圍更廣，因此可以為海岸結構設計提供依據。

N-S方程； VOF方法； 動量源； 直墻防波堤； 波壓力

近年來，有限元數值分析軟件的出現，增加了海岸工程數值水槽計算的可行性和有效性，成為目前研究波浪與海上結構物相互作用的重要手段。而數值波浪水槽研究的一個關鍵問題是要有效地消除波浪遇到建筑物產生的反射波。有學者進行了深入探索。例如，Brorsen和Larsen[1]提出了適合于邊界積分方程的非線性波浪的源項造波方法。Arai等[2]通過在水槽尾端一定區域設置速度衰減區，采用指數函數形式減小垂向速度。Lin和Liu[3]提出了基于N-S方程的質量源造波方法，將附加質量源項添加到連續方程，模擬了規則波與不規則波。劉海青和趙子丹[4]使用有限元方法對N-S方程進行離散，并在入射邊界布設人工衰減區，吸收到達入射邊界的反射波。高學平等[5]使用線源造波方法對駐波進行計算模擬，該法能夠很好地吸收波浪遇到建筑物的反射波。高山[6]利用邊界元離散方法和混合歐拉一拉格朗日捕捉自由面方法構建數值水槽，并設計了一種紡錘形的阻尼消波器使其具有雙向消波功能和低通濾波功能。周勤俊等[7]利用FLUENT商業軟件，將入射波場作為人工的分布源項加入到動量方程中，提出了一種適用于VOF方法的造波和消波方法。林鵬智等[8]通過基于VOF方法追蹤自由面的二維數值波浪水槽對直立防浪堤進行數值模擬研究。董志和詹杰民[9]基于不可壓縮流體方程并采用VOF方法，提出了動邊界造波的數值方法，建立了能夠模擬弱非線性波的數值波浪水槽。何軍等[10]利用VOF方法對于規則波作用下T型堤的水力學特性進行模擬。黃華等[11]對于N-S方程，采用FVM(Finite Volume Method)法進行離散求解，在入口邊界處，模擬活塞推板運動產生了入射波，對非線性二階Stokes波進行了仿真模擬。張博杰和張慶河[12]基于開源程序OpenFOAM，通過在質量守恒方程中添加質量源來實現域內源造波，采用阻尼消波，可以較好地模擬行進波和立波，并且能夠較好地避免邊界反射及二次反射。

基于源項造波理論，本文采用FLUENT軟件，通過二次開發實現了數值水槽的造波和消波功能，建立了可以有效模擬線性波浪和多種非線性規則波(如Stokes波、孤立波等)的數值波浪水槽，分析了造波和消波的有效性，對直立式防波堤波浪力進行了數值研究。將數值計算結果與試驗結果，以及按照我國規范方法計算的結果進行了比較，所得結論對海岸結構設計有指導意義。

1 數學模型

1.1 控制方程

假設流體是不可壓縮的，則描述流體運動的控制方程包括以速度和壓力為變量的連續性方程和動量方程。連續性方程為

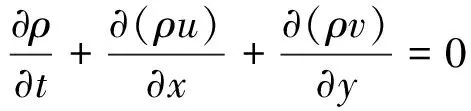
(1)

動量方程為

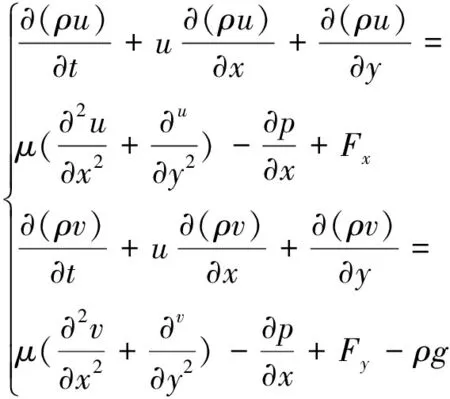
(2)

式中，u和v分別是x和y方向上的速度分量，p是壓強，(是動力學黏性系數，g為重力加速度。Fx和Fy分別是在x和y方向上的附加動量源項。

1.2 數值造波和消波方法

數值水槽不僅需要造波，也需要消波，尤其是在研究波浪與結構物的相互作用時，有效地消除入射波與結構物相互作用后的反射波至關重要。根據源造波理論，可以在連續方程中，或在動量方程中，或同時在兩個方程中添加源項達到造波和消波的目的。本文采用在動量方程中添加源項，基本思想是通過控制方程推導出源項，源項的作用是對造波區和消波區的流體增加和減少隨時間進行周期性變化的動量，進行數值模擬。

選擇不考慮黏性作用的歐拉方程推求各區域源項的表達式。先將x方向上添加源項和未添加源項的動量方程分別離散為

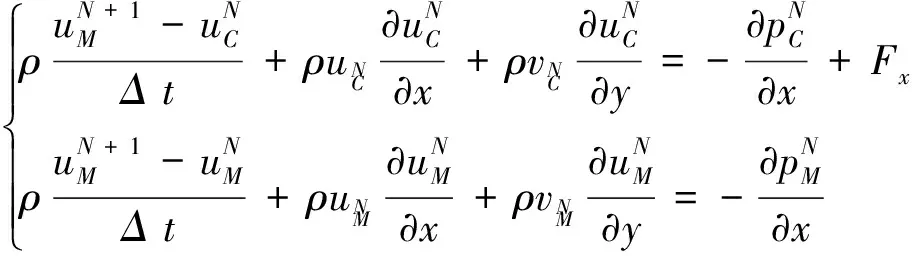
(3)

假設，造波區波動場為

(4)

前端消波區波動場為

(5)

尾端消波區波動場為

(6)

式中：N和(N+1)分別代表N和(N+1)時刻的值；M、l、j分別代表離散值、來波值和計算值；c=c(x)是與空間位置有關的光滑過渡加權函數。

將以上各區的速度和壓力表達式(4)-(6)代入式(3)，聯立方程求解，得到水槽中各功能設置區內的動量源項。本文以造波區為例，源項表達式如下：

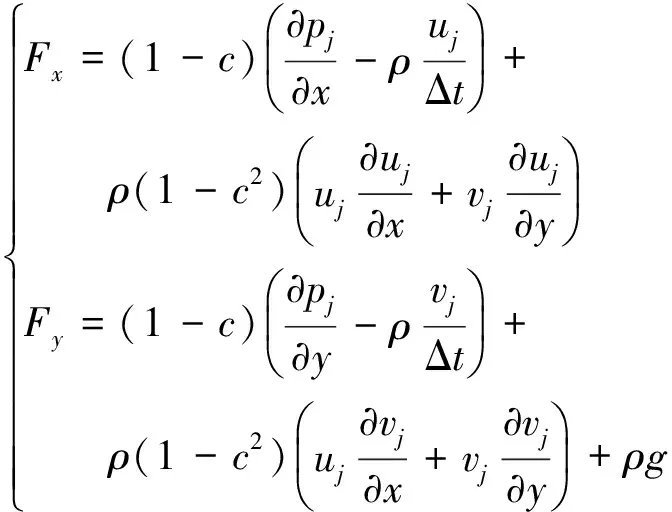
(7)

將各區的源項表達式采用C語言編程，通過FLUENT軟件的UDF接口分別代入到動量方程式(2)中，進而實現水槽中各功能區的造波和消波。

2 模型建立與網格劃分

模擬二維數值水槽時，在Gambit中進行網格的建立。為了更好地捕捉自由液面，水面處一個波高范圍內進行適當的加密，采用結構化網格進行劃分。網格劃分時，沿著水槽的長度方向一個波長內80～100個網格，高度方向一個波高內20個網格。水槽部分網格見圖1,二維數值水槽模型見圖2。

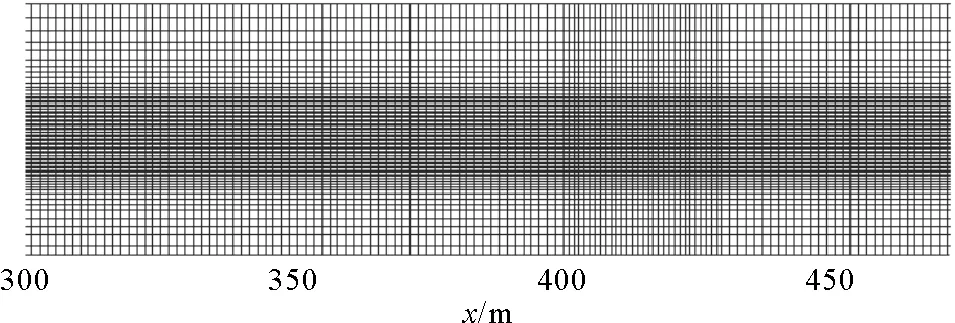
圖1 水槽網格劃分示意圖

邊界條件：數值水槽從左到右依次為造波區、前端消波區、工作區和尾端消波區。左邊界為對稱邊界，上邊界為壓力出口邊界，下邊界和右邊界設置為固壁邊界。

圖2 二維數值水槽分區及邊界條件示意圖

初始條件：流場的初始速度為零，迭代精度為0.001，每步最多迭代20次。在FLUENT中進行模型設置，湍流模型采用RNG的k-ε模型，壓力速度耦合PISO算法求解非定常狀態下的紊流問題。

3 數值波浪水槽模型的驗證

3.1 數值水槽造波的準確性

本文算例中，水槽的總長750 m，高度42.62 m，水深22.62 m，空氣高度范圍取20 m。造波區長度為120 m，前端消波區長度為120 m，工作區為310 m，尾端消波區為200 m。波高取為7.3 m，周期為8.9s，由于波陡大于0.1，這時候需要考慮波浪的非線性作用，因此使用Stokes波浪理論來進行研究。與高階的理論解相比，二階Stokes 波的計算結果和基于瞬態不可壓縮流的N—S方程求解結果相差甚微，考慮計算成本和計算精度，二階Stokes 波足以滿足工程需求。本文通過FLUENT中的UDF宏編寫程序，實現造波和消波，運行一段時間后，水槽中會出現穩定的波形。圖3～4給出了x=250m，x=350m 2個位置處的波高歷時曲線圖。由圖可見，與理論波面曲線比較，建立的數值水槽能產生歷時較長穩定的波浪，計算值與理論值吻合較好。

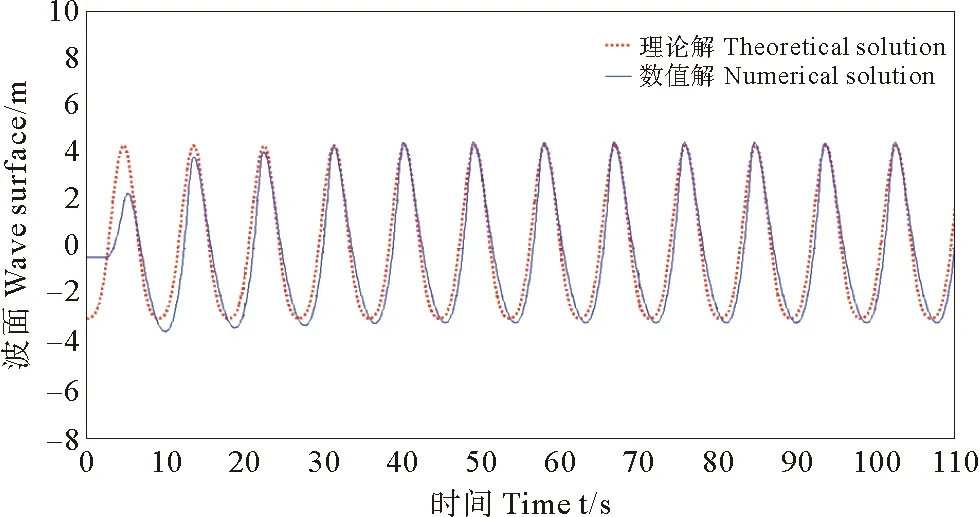
圖3 x=250 m 波面時間變化曲線

3.2 網格依賴性檢驗

數值水槽沿長度方向的網格長度分別取值dx=1.2,1.5,2m，計算時間步長dt取值為0.005，0.01s,在水槽x=250m位置處設置波面變化監測點，圖5為3種網格劃分方案在時間步長為0.005s時波面歷時變化計算結果，圖6為3種網格劃分方案在時間步長為0.01s時波面歷時變化計算結果。由圖可見，不同方案計算結果基本吻合。本文在計算中取dx=1.5，dt=0.01s作為網格劃分標準。

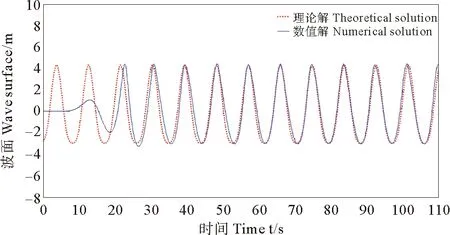
圖4 x=350m波面時間變化曲線

圖5 dt=0.005s時波面時間變化曲線

圖6 dt=0.01s時波面時間變化曲線

3.3 前端消波區的消波效率

將水槽右邊界設為wall，去掉末端消波區，這樣入射波遇到直墻后會發生全反射。當入射波與反射波疊加，水槽中會出現駐波的現象，而且駐波的波幅為入射波的2倍。圖7是直墻前波高最大時一個波長左右的波面曲線，圖8為x=460 m處的波面歷時曲線，波浪穩定后可以看到波高大約是入射波高的2倍，這說明前端消波區能較好的吸收直墻反射的波浪。

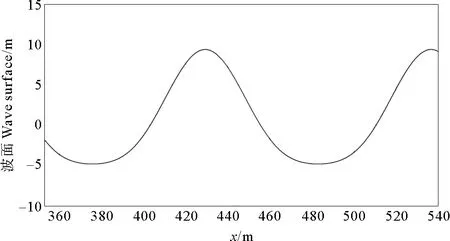
圖7 墻前駐波波面曲線

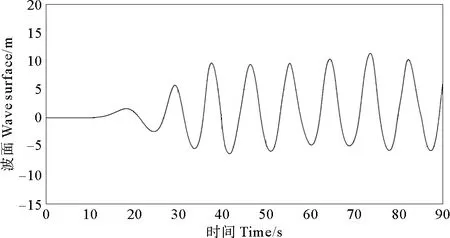
圖8 x=460 m處波面歷時曲線

4 非線性波浪作用于直墻防波堤的數值模擬

4.1 直墻防波堤數值模型的建立

在數值水槽中，防波堤距離左邊界400m，模擬波浪的波高取7.3m，周期為8.9s。試驗分別模擬極端高水位，設計高水位，以及設計低水位下波浪與建筑物的相互作用，即，水深分別是22.62，21.88，以及19.68m。波浪水槽示意圖見圖9，其中，H為堤前波高，m為外側坡度，L為波長，d為水深，d1堤前水深，B為平臺寬度。左邊界為對稱邊界，上邊界設置為壓力出口，底部邊界、堤壩結構以及右邊界設置均為固壁邊界。

采用結構化網格和非結構化網格相結合，在直墻防波堤附近使用三角形網格，在其他區域使用四邊形結構化網格。為了較好地捕捉自由液面，在液面上下一個波高的范圍內加密，網格劃分見圖10。防波堤模型斷面尺寸與堤身迎浪面布置的壓力監測點位置見圖11。

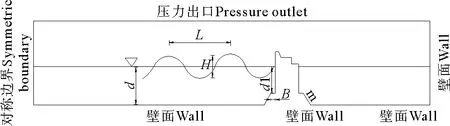
圖9 直墻防波堤數值模型示意圖

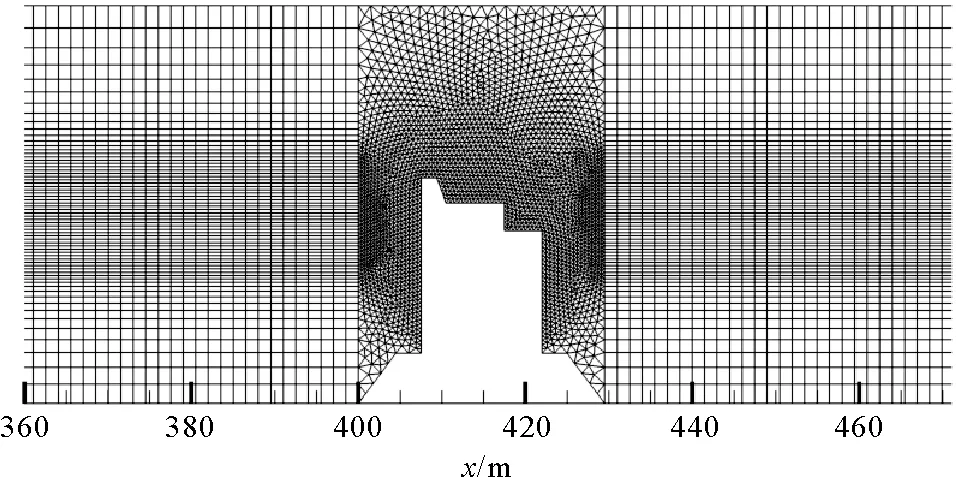
圖10 數值水槽網格劃分示意圖

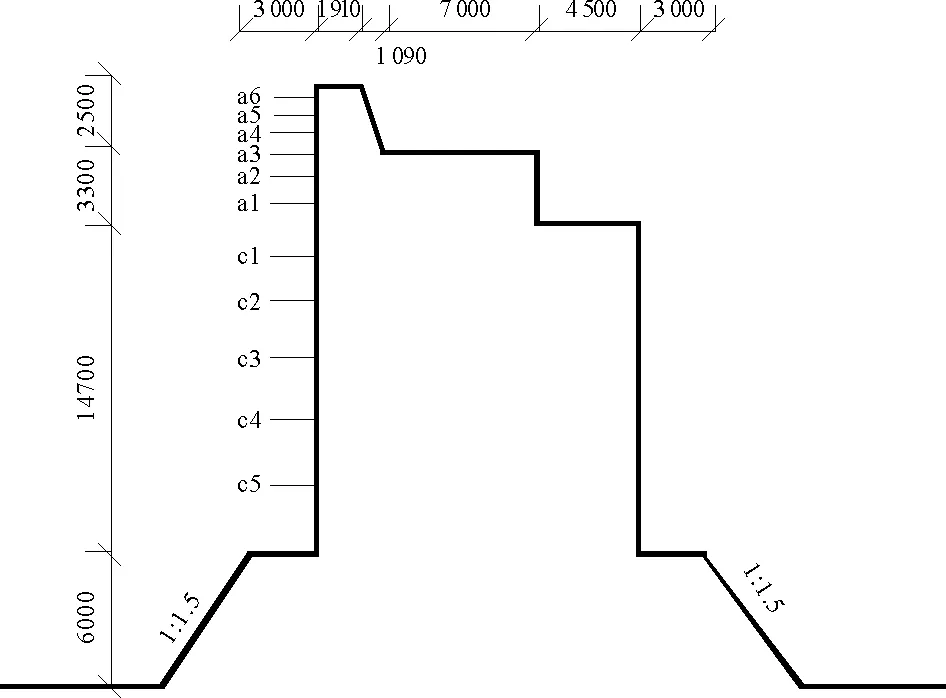
圖11 模型尺寸與堤面壓力測點分布圖

4.2 直墻防波堤波浪力的物理模型試驗

物理模型試驗采用的是某擴建工程東護岸斷面物理模型試驗。模型試驗是在海軍工程設計研究院工程綜合試驗研究中心進行。試驗在長50.0m、寬1.2m、深1.2m的不規則波水槽中進行。水槽一端為低慣量直流式電機不規則造波機。造波機產生的最大波高為0.23m。波浪水槽的另一端為鋼質多孔的消能設施，其反射率小于5%。水槽在寬度方向上分兩格，分別為0.8m和0.4m，寬度0.8m的一格放置模型，另一格用于消能。

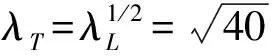
圖12 物理試驗模型斷面圖

序Order水位Waterlevel水深d/mm波高H/mm周期T/s1極端高水位Extremehighwaterlevel565．5182．51．4072設計高水位Designhighwaterlevel547．0182．51．4073設計低水位Designlowwaterlevel492．0182．51．407

注：波高模型比尺為λH=λ=40，周期模型比尺為λT=λ0.5。

Notes: Wave height model scale isλH=λ=40, Wave period model scale isλT=λ0.5.

4.3 波壓力沿堤面分布的對比

由于波浪的作用，在海堤上會形成垂直于堤面的波浪正壓力和波浪負壓力，本文分別測定了極端高水位，設計高水位，設計低水位時候的各個測點的最大正向波壓力和最大負向波壓力。將3種水位下數模和物模波壓力值與我國《海堤工程設計規范》[14]計算的波壓力值進行對比，并繪制壓力曲線包絡圖(見圖13-15)。

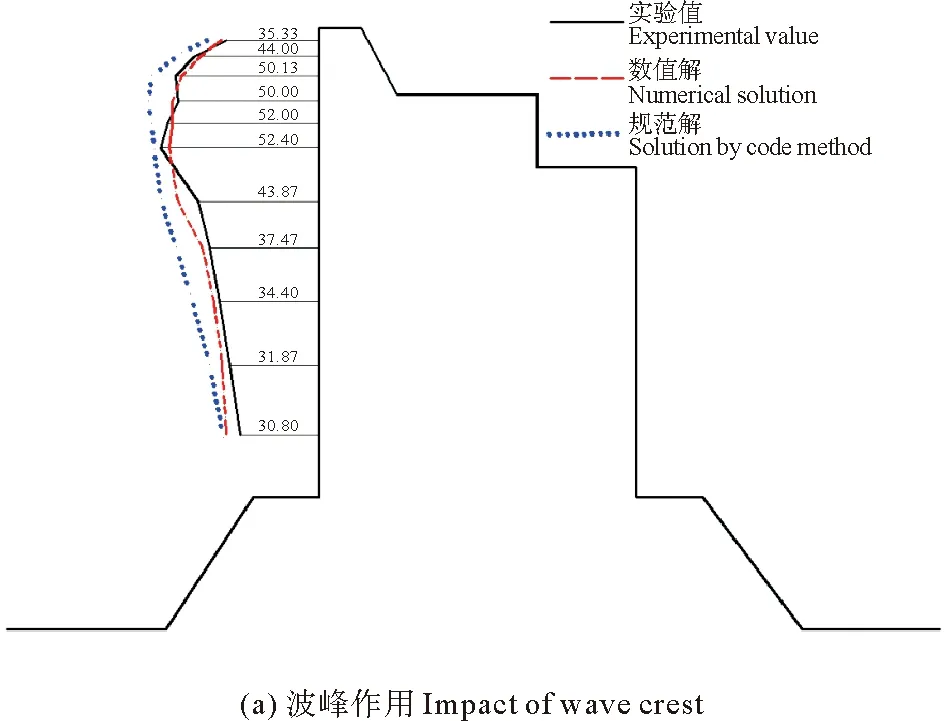
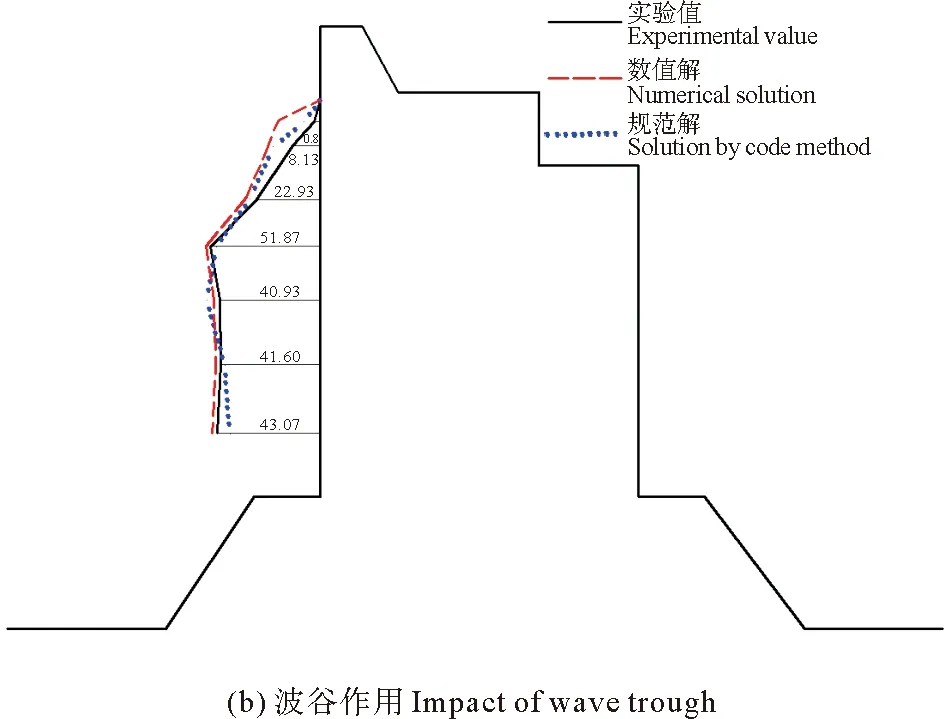
圖13 極端高水位波浪壓力包絡圖

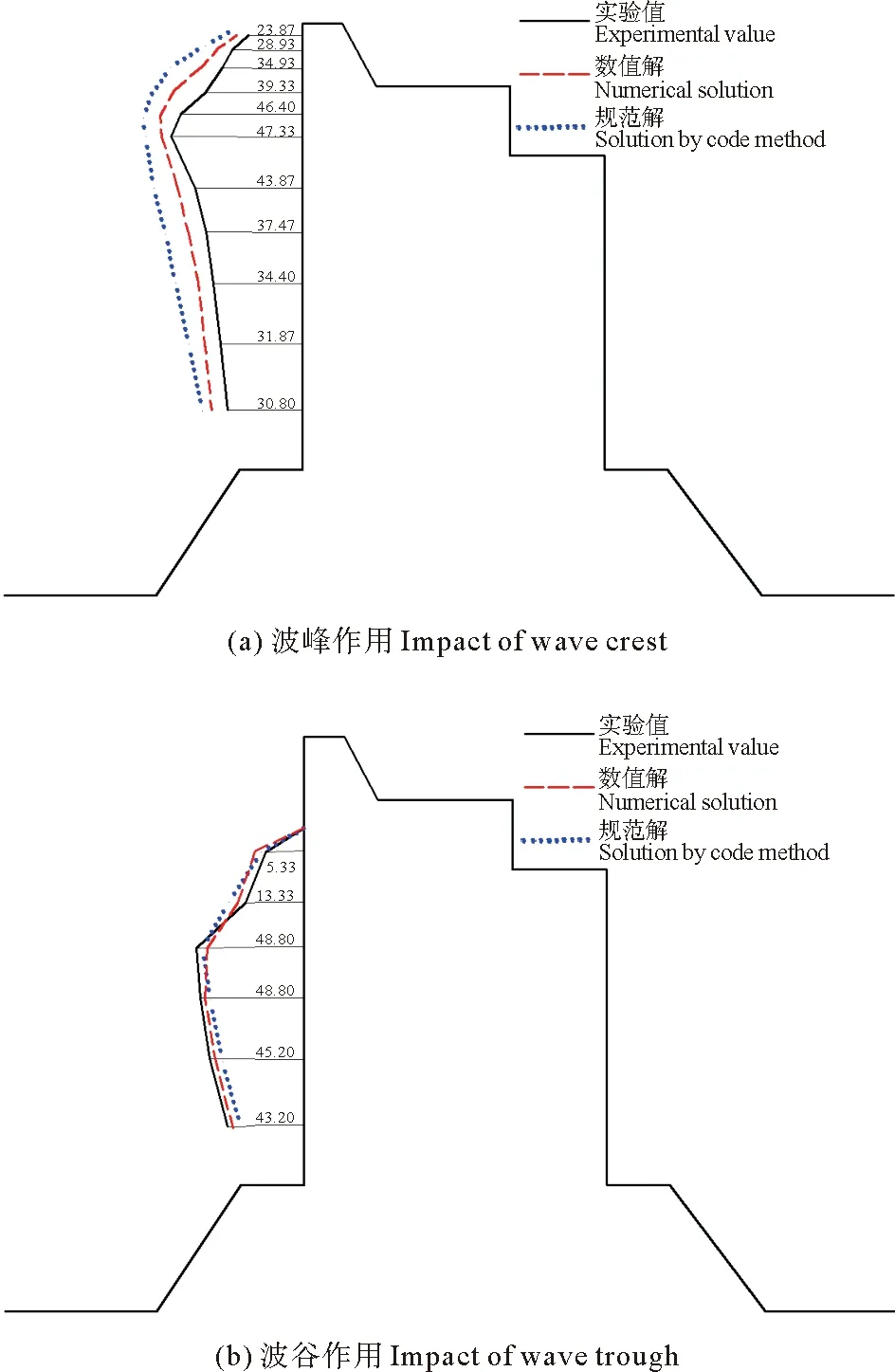
圖14 設計高水位波浪壓力包絡圖

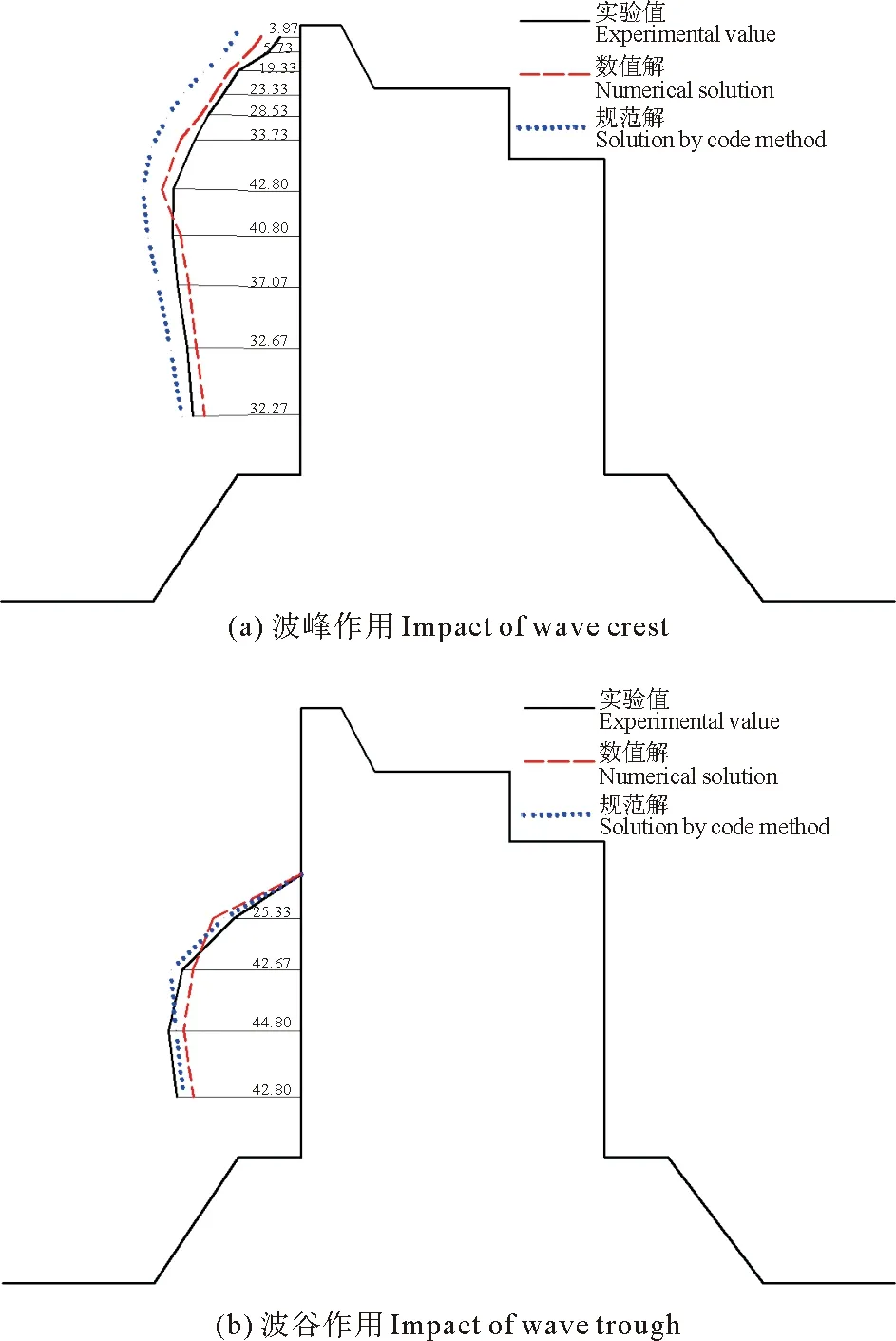
圖15 設計低水位波浪壓力包絡圖

由圖可見，數模波壓力包絡圖和物模波壓力包絡圖吻合比較好，說明本文構建的數值水槽可以有效的模擬波浪與結構物相互作用。同時本文中，數模計算和物模試驗得到的波峰作用時最大波浪壓力值均比規范值要小，主要原因規范設計中，為了保證結構的安全性，會增加安全性系數，從而會使規范值變大。最后，物模試驗和數模計算中，均出現越浪現象，建議對胸墻進行適當加固。

5 結論

通過物理模型試驗與計算的對比分析，得到如下結論：

(1)基于非線性波浪理論和源項造波理論，本文在動量方程中添加附加源項建立的二維數值波浪水槽，能夠產生歷時較長的穩定的非線性規則波浪，能夠很好地吸收波浪遇到建筑物產生的反射波，消除建筑物反射波的影響，計算結果與理論解析解吻合較好。

(2)直墻防波堤上波浪力的計算結果表明，數模波壓力包絡圖和物模波壓力包絡圖吻合較好。與規范計算值進行比較時，在波峰作用時，數模和物模值均比規范值小，這是由于規范出于工程安全考慮的原因。

綜上所述，本文所采用的動量源造波、消波方法原理清晰，形式簡單，計算穩定，可以高效率的進行波浪與海上結構物的作用研究，并為實際工程方案的設計提供參考，有較高的實用價值。

[1] Brorsen M, Larsen J. Source Generation of nonlinear gravity waves with boundary integral equation method[J]. Coastal Engineering, 1987, 11: 93-113.

[2] Arai M, Paul U K, Cheng L-Y, Inoue Y. A technique for open boundary treatment in numerical wave tanks[J]. Journal of the Society Naval Architects of Japan, 1993, 173: 45-50.

[3] Lin P Z, Liu P L F. Internal wave-maker for Navier-stokes equations models[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 1999, 125(4): 207-217.

[4] 劉海青, 趙子丹. 數值波浪水槽的建立與驗證[J]. 水動力學研究與進展: A輯, 1999, 14(1): 8-14. Liu Hai-qing, Zhao Zi-dan. Numerical Wave Flume and Its Verification[J]. Chinese Journal of Hydrodynamics: A edition, 1999, 14(1): 8-14.

[5] 高學平, 曾廣冬, 張亞. 不規則波浪數值水槽的造波和阻尼消波[J]. 海洋學報, 2002, 24(2): 127- 132. Gao Xue-ping, Zeng Guang-dong, Zhang Ya. Wave generation and damping absorber of irregulat waves with MAC method[J]. Acta Oceanologica Sinica, 2002, 24(2): 127- 132.

[6] 高山. 二維數值波浪水槽模式的建立和應用及浪流相互作用研究[D]. 青島:中國海洋大學, 2003. Gao Shan. The Development and Applications of a 2-D Numerica1 Wave Tank and The Study of Wave-Current Interaction[D]. Qingdao: Ocean University of China, 2003.

[7] 周勤俊, 王本龍, 蘭雅梅, 等. 海堤越浪的數值模擬[J]. 力學季刊, 2005, 26(4): 629-633. Zhou Qin-jun, Wang Ben-long, Lan Ya-mei, et al. Numerical Simulation of Wave Overtopping over Seawalls[J]. Chinese Quarterly of Mechanics, 2005, 26(4): 629-633.

[8] Lin P, Xu W. NEWFLUME: A numerical water flume for two-dimensional turbulent free surface flows[J]. Journal of Hydraulic Research, 2006, 44(1): 79-93.

[9] 董志, 詹杰民. 基于VOF方法的數值波浪水槽以及造波、消波方法研究[J]. 水動力學研究與進展, 2009, 24(1): 15-21. Dong Zhi, Zhan Jie-min. Comparison of existing methods for wave generating and absorbing in VOF-based numerical tank[J]. Chinese Journal of Hydrodynamics, 2009, 24(1): 15-21.

[10] 何軍, 蔣昌波, 李冬, 等. T型防波堤與波浪相互作用的數值研究[J]. 海洋工程, 2010, 28(1): 50-57. He Jun, Jiang Chang-bo, Li Dong, Deng Bin. Numerical study on T-type breakwaters interaction with wave[J]. The Ocean Engineering, 2010, 28(1): 50-57.

[11] 黃華, 鄧冰, 陳昱松, 等. 數值波浪水槽構建與二階Stokes波仿真[J]. 系統仿真學報, 2012, 24(1): 227-231. Huang Hua, Deng bing, Chen Yu-Song, et al. Building of numerical wave tank and 2nd stokes wave simulation[J]. Journal of System Simulation, 2012, 24(1): 227-231.

[12] 張博杰, 張慶河. 基于OpenFOAM開源程序的無反射數值波浪水槽[J]. 中國港灣建設, 2012, 5: 1-3. Zhang Bo-jie, Zhang Qing-he. 2D numerical wave flume without reflection based on openFOAM[J]. China Harbour Engineering, 2012, 5: 1-3.

[13] JTJ/T234-2001. 波浪模型試驗規程[S]. 北京: 人民交通出版社, 2002. JTJ/T234-2001. Wave Model Test Regulation[S]. Beijing: China Communications Press, 2002.

[14] SL435-2008. 海堤工程設計規范[S]. 北京: 中國水利水電出版社, 2008. SL435-2008. Code for Design of Sea Dike Project[S]. Bejing: China Water Power Press, 2008.

責任編輯 陳呈超

Calculation of Wave Pressure on Upright Section of Vertical Breakwater

YU Long-Ji1，DONG Sheng1，DUAN Cheng-Lin1，ZHANG Hua-Chang2

(1.College of Engineering, Ocean University of China, Qingdao 266100, China; 2.Navy Engineering Design and Research Institute, Qingdao 266100, China)

Based on Navier-Stokes equations to describe the motion of incompressible fluid, the volume of fluid (VOF) method is adopted to track the free surface. According to the continuity equation and momentum equation, the source function is deduced. Different source terms will be added to the momentum equation in each functional area of the numerical flume on the basis of nonlinear theory of wave(second-order Stokes) and the UDF function of the secondary development of FLUENT software to realize the functions of wave generation and absorption. By this method wave reflection at outflow boundary and secondary reflection at the incident boundary from a marine structure. can effectively eliminated in order to obtain stable wave field. This approach is applied to the numerical simulation of wave pressure on vertical breakwater. The effectiveness of wave making and wave elimination is analyzed. Then, the numerical simulation of wave pressure on vertical breakwater is carried out. To realize the accuracy of the calculation and the high efficiency, the flow field is meshed by structured and unstructured grids. Triangular mesh is used near the vertical breakwater and structured grid is used in other regions. The mesh of a wave height in the free surface needs to be densified in order to capture the free surface better.Results are consistent with the theoretical solution of second-order non-linear Stokes wave. This shows that the proposed numerical wave flume based on software FLUENT could eliminate the second reflecting wave of building and realize long time of wave. It provides reference for the design of practical engineering project, and has high practical value. The maximum forward wave pressure and the maximum negative pressure of each measurement point are calculated at extreme high water level, design high water level and low water level. The results compared with both experimental data and the results by empirical equations show that simulated wave pressure fit measured results very well. In addition, the numerical method can be used to calculate the various conditions with different angles of breakwater slope. Because the numerical calculation can be applied in a wider scale than empirical equation method, its results can provide a solid support for coastal structural design.

Navier-Stokes equations; VOF method; momentum source; vertical breakwater; wave pressure

國家自然科學基金項目(51279186;51479183)資助 Supported by Natural Science Foundation of China (51279186; 51479183)

2014-10-12；

2015-12-10

于龍基(1989-)，男，碩士生。E-mail: yulongji_ouc@163.com

?? 通訊作者： E-mail: dongsh@ouc.edu.cn

P753

A

1672-5174(2016)12-126-07

10.16441/j.cnki.hdxb.20140429

于龍基， 董勝， 段成林， 等. 直立式防波堤迎浪面波壓力計算研究[J]. 中國海洋大學學報(自然科學版), 2016, 46(12)： 126-132.

YU Long-Ji， DONG Sheng， DUAN Cheng-Lin, et al. Calculation of wave pressure on upright section of vertical breakwater[J]. Periodical of Ocean University of China, 2016, 46(12)： 126-132.