基于模糊滑模的多機器人系統編隊控制

錢殿偉

(華北電力大學 控制與計算機工程學院，北京 102206)

?

基于模糊滑模的多機器人系統編隊控制

錢殿偉

(華北電力大學 控制與計算機工程學院，北京 102206)

針對多機器人編隊控制問題，提出了一種滑模控制與模糊邏輯相結合的控制方法。運用領航—跟隨法，建立機器人系統的動力學模型。該模型具有不確定性，在不確定性上界未知的假設條件下，運用模糊邏輯，設計模糊補償器，以逼近系統的不確定性部分。基于Lyapunov理論，證明所設計的模糊滑模編隊控制系統具有漸近穩定性，同時模糊補償器的逼近誤差是收斂的。仿真結果表明，該方法可使多機器人系統迅速地形成所期望的隊形，并在運動中保持該隊形。

多機器人；編隊控制；不確定性；滑模控制；模糊邏輯

多機器人編隊系統相比復雜單機器人系統具有諸多優點，在工業制造、地理勘測、太空探索等領域具有廣泛的應用前景，目前已成為研究的熱點問題之一。多機器人編隊控制方法主要有行為法[1]、虛擬結構法[2]、領航—跟隨法[3-4]及人工勢場法[5]等。其中，領航—跟隨法因其控制簡單，易于實現分布式控制，可將整個編隊控制問題簡化為若干獨立的軌跡跟蹤控制問題，在多機器人編隊控制方面應用廣泛。采用領航—跟隨法，常用的控制算法有反饋線性化[6]、預測控制[7]、滑模控制[8-9]及智能控制[10-11]等。

就模型而言，多機器人編隊控制分為基于運動學模型的控制和基于動力學模型的控制。在實際應用中，多機器人編隊系統受到負載變化、參數攝動、測量噪聲、摩擦、傳動系統的非線性及外部擾動等不確定性的影響[3]。基于模型的控制方法難以克服不確定的影響，需要探尋更加有效的控制策略。

滑模控制具有不變性的特點，因其魯棒性強、響應快速和易于實現等特點被廣泛地研究[6, 10]。在滑模控制器設計中，為保證控制系統的穩定性，通常要假設已知不確定性的上界。就多機器人編隊控制問題而言，這個假設在實際中可能難以滿足。模糊邏輯具有以任意精度逼近非線性連續函數的能力[10]，是估計系統中不確定性的可行方法。

針對未知上界的不確定性，本文結合滑模控制和模糊邏輯，研究了多機器人系統編隊控制問題。首先，根據跟隨者與領航者的相對位置與相對相角，建立編隊系統的動力學模型；然后，采用模糊推理系統逼近系統中的不確定性，設計滑模控制器穩定相對位置與相對相角，應用Lyapunov條件證明控制系統的穩定性和逼近誤差的收斂性；最后，通過仿真實驗驗證所提出方法的有效性。

1 系統描述

本文以半徑為r的圓形非完整輪式移動機器人為對象，其理想運動學和動力學模型見文獻[9]。采用領航-跟隨者編隊方法，在一組由n個非完整移動機器人組成的編隊系統中，選機器人i為領航者，剩余n-1個為跟隨者。在跟隨者中，選擇跟隨者k與領航者i組成編隊控制模型，其結構如圖1所示。

在圖1中，跟隨者k與領航者i的相對相角和相對距離分別為

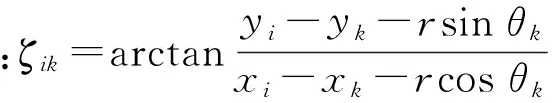
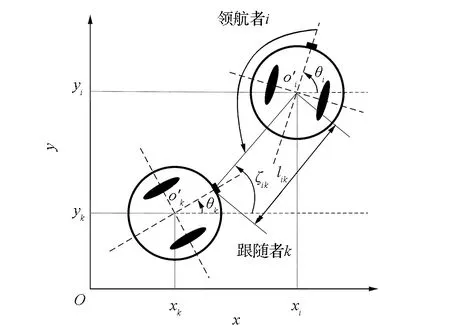
圖1 跟隨—領航者編隊控制模型

對相對相角(1)和位置(2)求二階導，令xik=[x1x2]T=[likψik]T，得到跟隨-領航者編隊控制的動力學模型的狀態空間表達式為

令φik=ψik+θi-θk，各參數矩陣描述如下

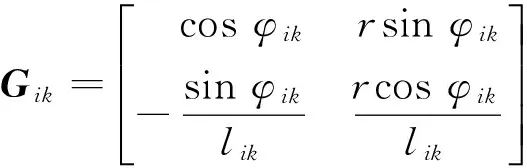
I2是2×2單位矩陣；Fik=[F1F2]T；Pik=[P1P2]T；Δk和Δi是2×2擾動矩陣；

式中：πkx、πky、πkθ、πix、πiy和πiθ∈R1分別為領航者和跟隨者的不確定性。

建模中主要假設為：領航者與跟隨者之間無通訊延遲；領航者與跟隨者均可知自身位置和速度；領航者通過通訊將其位置和速度傳遞給跟隨者。

2 控制系統設計及穩定性分析

2.1 模糊補償器的設計

模糊推理系統(FIS)的數學本質是從集合U∈Rm到V∈Rn的非線性映射，其結構圖如圖2所示。在圖2中，輸入向量a=[a1a2…am]T∈U，輸出向量b=[b1b2…bn]T∈V，第l條模糊規則為

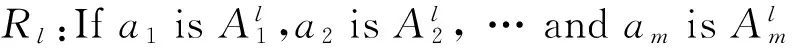
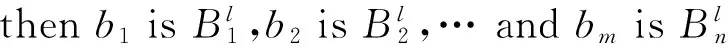
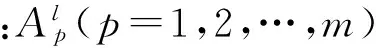
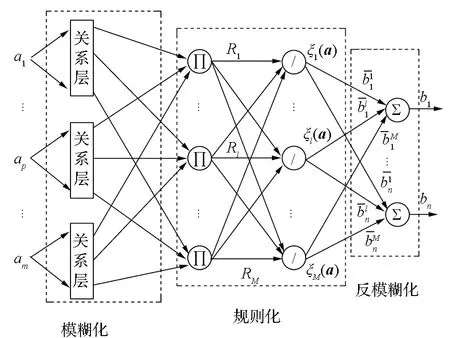
圖2 模糊推理系統結構圖

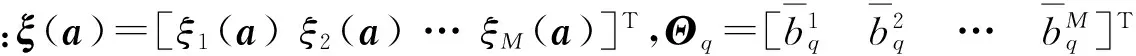
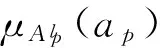
式中cp和σp分別代表此隸屬函數的中心和寬度。

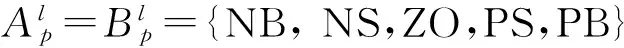
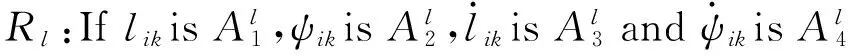
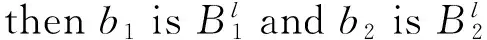
根據式(4)，不確定性的逼近值可描述為

設Θ存在最優參數矩陣Θ*，且Θ*滿足

式中:χ0為包含Θ的有界集合。

定義逼近誤差的最小值向量為

式中:ρ=[ρ1ρ2]T∈R2×1。

針對多機器人編隊設計的FIS是一個4輸入2輸出系統，輸入變量具有5個模糊子集，所以FIS的規則庫有54條模糊規則，即M=625。

2.2 滑模控制器的設計

定義滑模面

式中：sik(t)=[sik,1(t)sik,2(t)]T∈R2×1，xeik=xik-xdik∈R2×1為跟蹤誤差向量，xdik為期望軌跡向量，λ為一個2×2的正定矩陣。

定義參考向量

設計滑模控制律

式中:κ和η均為2×2的對角矩陣，即κ=diag(κ1,κ2)，η=diag(η1,η2)，其中κ1、κ2、η1和η2為設計參數；sign(sik)=[sign(sik,1) sign(sik,2)]T，sign(·)為符號函數。

2.3 穩定性證明

定理1對于機器人編隊系統式(5)，設計模糊補償器式(7)和滑模控制律式(12)。如定義參數自適應律為

式中:Γq>0∈R1，κq>0，ηq>|ρq|(q=1,2)，那么多機器人編隊控制系統式(5)是漸近穩定的。

證明選取李雅普諾夫函數：

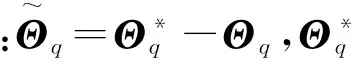
由式(10)和式(11)可知

將式(3)和式(16)依次代入式(15)可得

將式(9)和式(12)代入式(17)可得

將參數自適應律式(13)代入式(18)可得

考慮ηq>|ρq|，將其代入式(19)可得

因此，基于滑模和模糊補償器的編隊控制系統具有漸近穩定性。

3 仿真結果

根據上文設計的控制器進行仿真實驗，驗證該方法的有效性。采用模糊補償器和滑模控制器的控制方法結構圖如圖3所示。

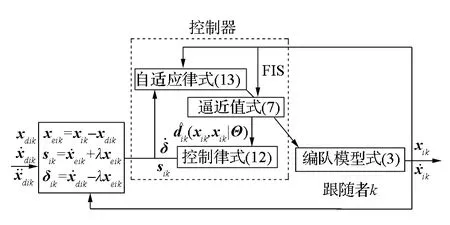
圖3 控制方法結構圖

設圓形機器人的半徑r=0.05 m；選擇15%的參數波動Δi=Δk=diag(rand,rand)，式中rand表示一個在閉區間[-0.15,0.15]上均勻分布的隨機數；考慮如下周期性外部擾動πix=πiy=πiθ=0.5sin(2πt)；πkx=πky=πkθ=0.2sin(πt)。

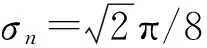
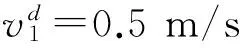
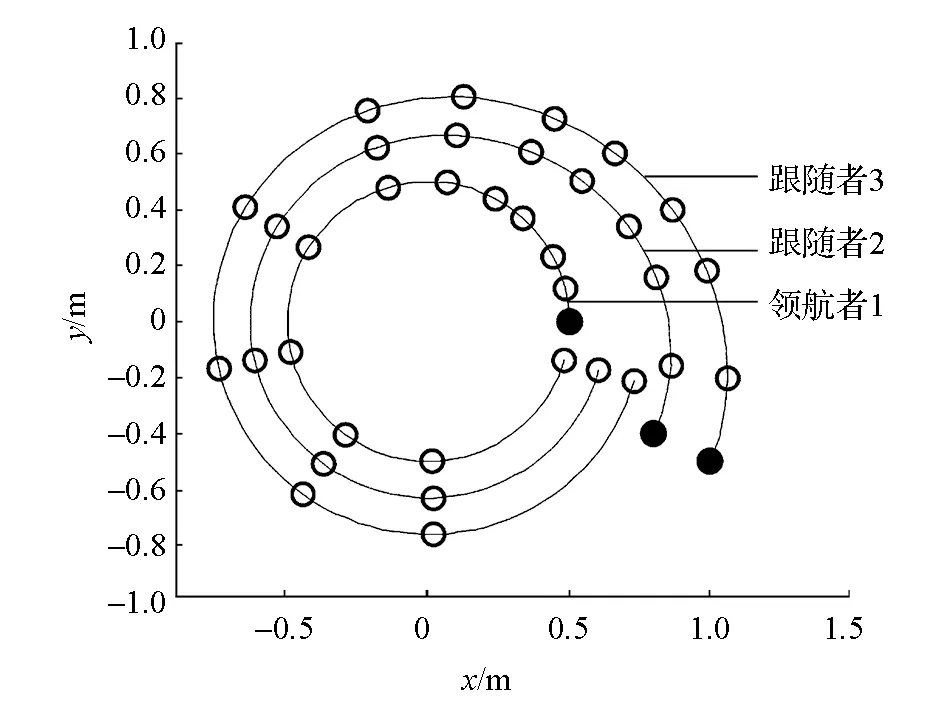
圖4 直線編隊跟蹤圓形軌跡

采用文[12]中一階滑模控制方法和二階滑模控制方法與本文所提出模糊補償器與滑模控制器相結合的控制方法進行對比實驗，仿真結果如圖5～8所示。從圖5看出，在不確定性上界未知的假設條件下，帶模糊補償器的滑模控制方法可以使3個機器人迅速地收斂到期望隊形，并以較高的跟蹤精度保持期望隊形運動；滑模控制方法的動態響應時間較長，且由于不確定性的影響在編隊形成后存在明顯波動。

滑模控制的不連續性導致了控制器輸出存在抖振現象，如圖6和圖7，用飽和函數替換式(12)中的符號函數可以改善這種現象。從圖8看出，當編隊系統進入滑動模態后，由于不確定性的影響會使系統在滑模面附近產生抖動，但此時lik和ψik已進入平衡點鄰域內，故系統保持局部漸近穩定。由圖9可知，模糊補償器可以有效地跟蹤編隊系統的未知的不確定項。

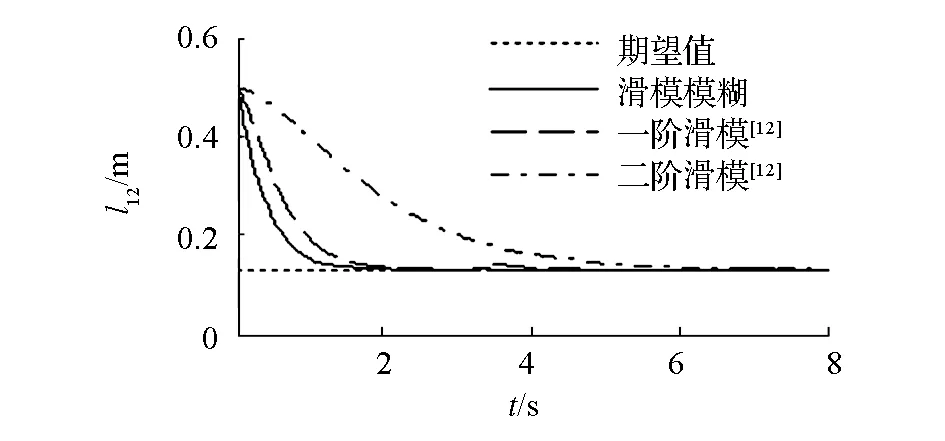
(a)相對距離l12

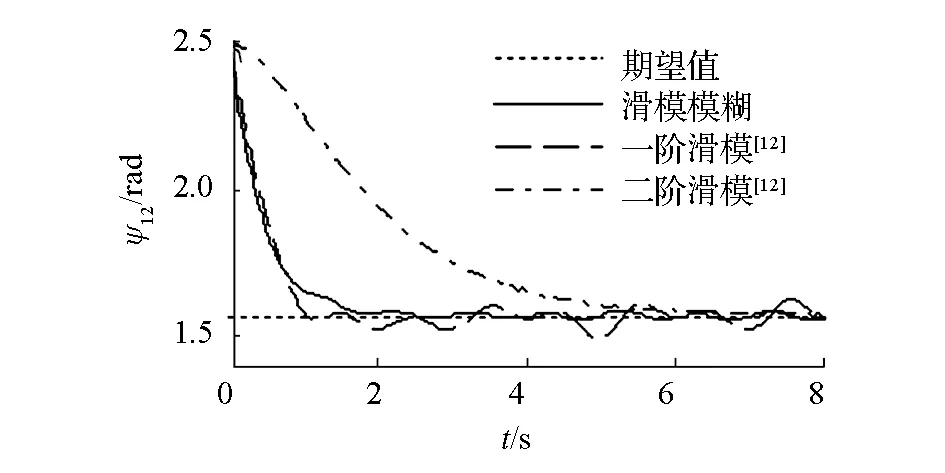
(b)相對相角ψ12

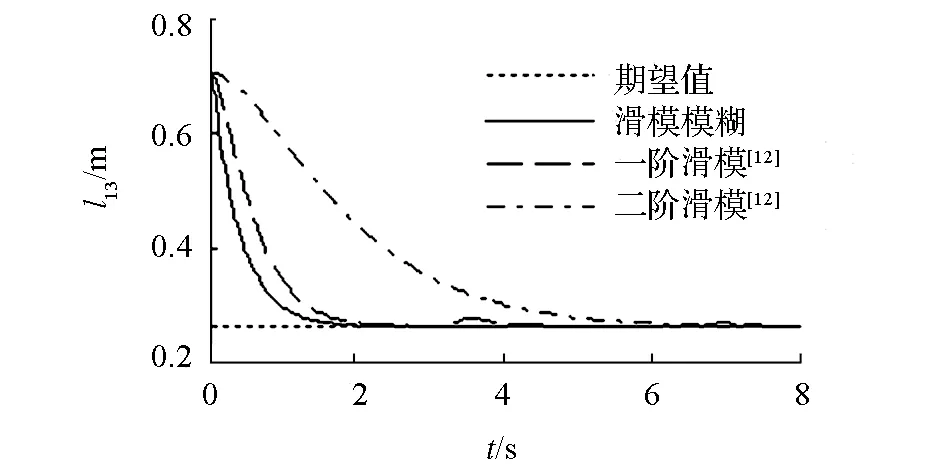
(c)相對距離l13

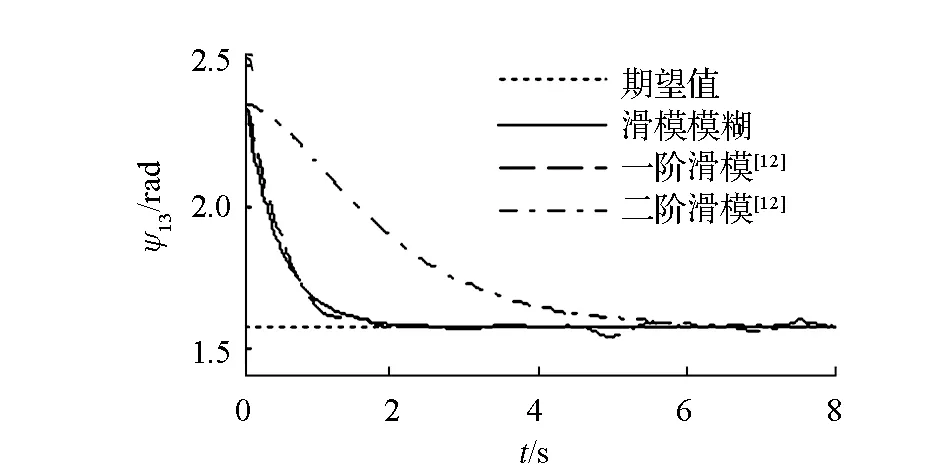
(d)相對相角ψ13

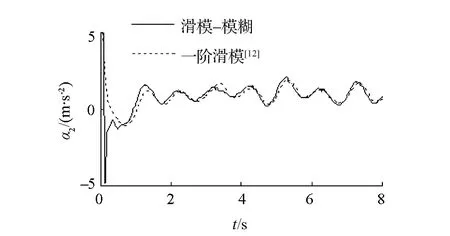
(a)本方法與一階滑模

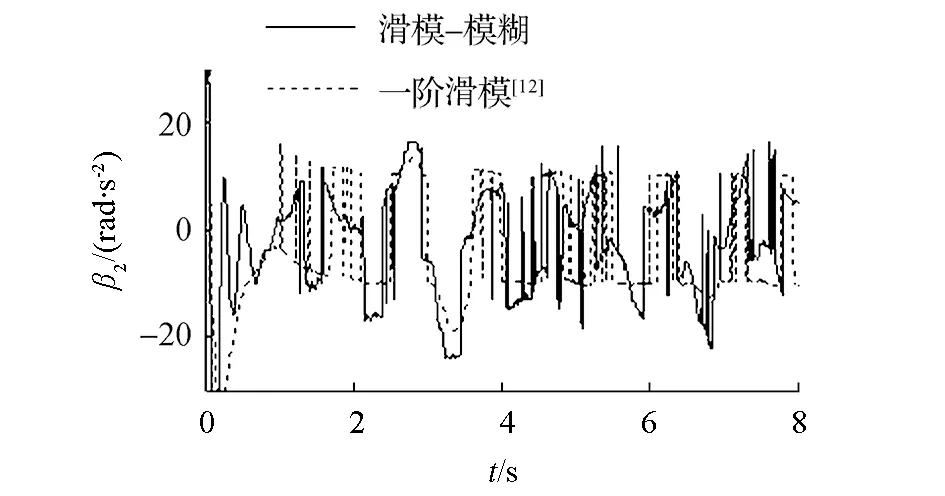
(b)本方法與一階滑模

(c)二階滑模

(d)二階滑模

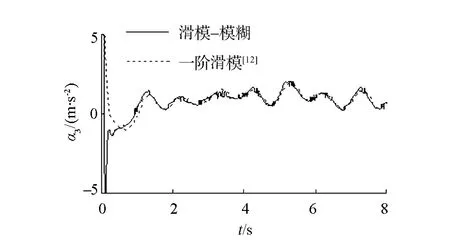
(a)本方法與一階滑模

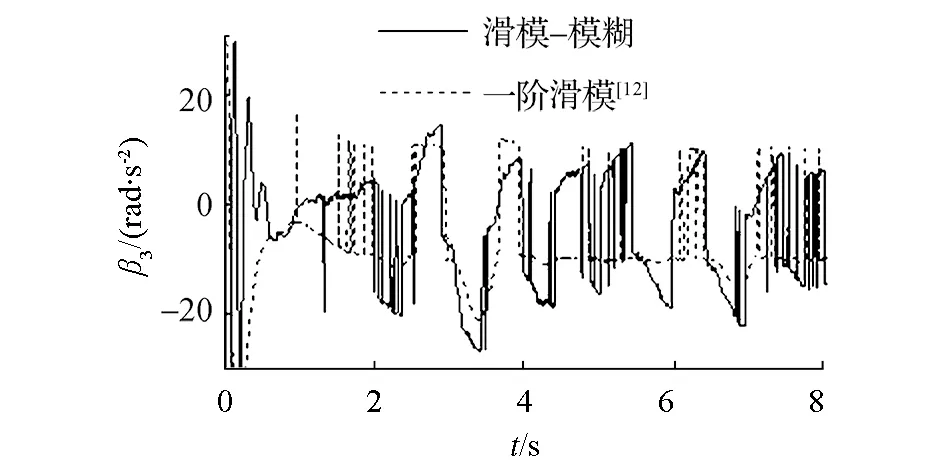
(b)本方法與一階滑模

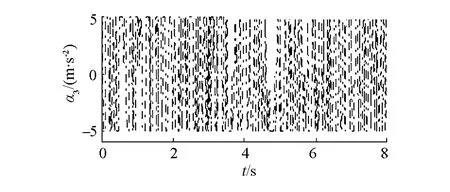
(c)二階滑模

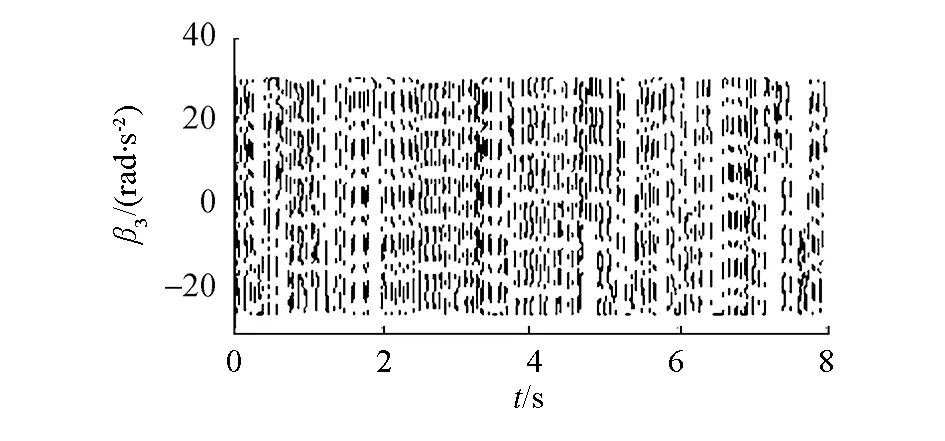
(d)二階滑模

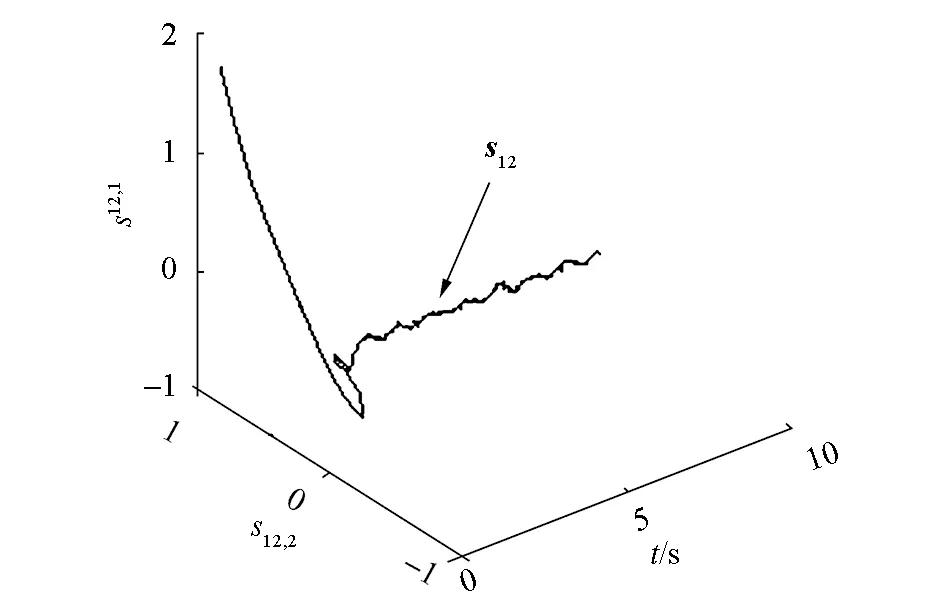
(a)滑模向量s12

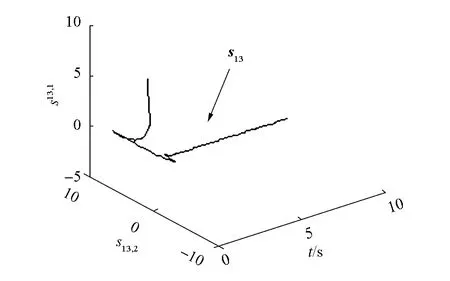
(b)滑模向量s13

(a)d12,1

(b)d12,2

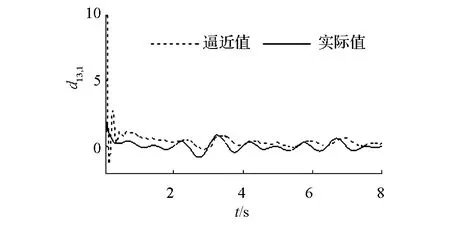
(c)d13,1

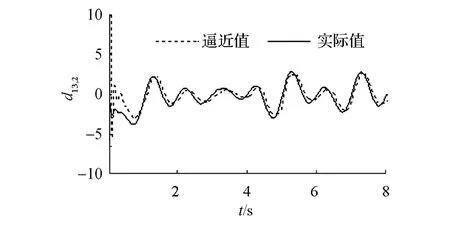
(d)d13,2

4 結束語

本文針對多機器人編隊控制問題，提出了一種模糊補償器與滑模控制器相結合的控制方法。運用領航—跟隨法建立系統動力學模型，將整個編隊控制問題轉化為若干跟隨者的軌跡跟蹤問題。利用模糊邏輯和滑模控制方法對跟隨者設計模糊補償器和滑模控制器，并證明系統的穩定性。仿真結果與滑模編隊控制方法進行對比，驗證了本文所提出的控制方法可以有效的克服未知上界的不確定性對編隊系統的影響；實現多機器人編隊在期望隊形下對指定軌跡的跟蹤。

[1]HUDA M N, YU Hongnian, CANG Shuang. Behaviour-based control approach for the trajectory tracking of an underactuated planar capsule robot[J]. IET control theory & applications, 2015, 9(2): 163-175.

[2]SADOWSKA A, VAN DEN BROEK T, HUIJBERTS H, et al. A virtual structure approach to formation control of unicycle mobile robots using mutual coupling[J]. International journal of control, 2011, 84(11): 1886-1902.

[3]楊麗, 曹志強, 譚民. 不確定環境下多機器人的動態編隊控制[J]. 機器人, 2010, 32(2): 283-288. YANG Li, CAO Zhiqiang, TAN Min. Dynamic formation control for multiple robots in uncertain environments[J]. Robot, 2010, 32(2): 283-288.

[4]WANG Jinliang, WU Huaining. Leader-following formation control of multi-agent systems under fixed and switching topologies[J]. International journal of control, 2012, 85(6): 695-705.

[5]王奎民, 趙玉飛, 侯恕萍, 等. 一種改進人工勢場的UUV動礙航物規避方法[J]. 智能系統學報, 2014, 9(1): 47-52. WANG Kuimin, ZHAO Yufei, HOU Shuping, et al. Dynamic obstacle avoidance for unmanned underwater vehicle based on an improved artificial potential field[J]. CAAI transactions on intelligent systems, 2014, 9(1): 47-52.

[6]ZHAO Weihua, GO T H. Quadcopter formation flight control combining MPC and robust feedback linearization[J]. Journal of the franklin institute, 2014, 351(3): 1335-1355.

[7]GUILLET A, LENAIN R, THUILOT B, et al. Adaptable robot formation control: adaptive and predictive formation control of autonomous vehicles[J]. IEEE robotics & automation magazine, 2014, 21(1): 28-39.

[8]LIU Hui, LI Junfeng. Terminal sliding mode control for spacecraft formation flying[J]. IEEE transactions on aerospace and electronic systems, 2009, 45(3): 835-846.

[9]QIAN Dianwei, TONG Shiwen, GUO Jinrong, et al. Leader-follower-based formation control of nonholonomic mobile robots with mismatched uncertainties via integral sliding mode[J]. Proceedings of the institution of mechanical engineers, part I: journal of systems and control engineering, 2015, 229(6): 559-569.

[10]袁媛, 焦繼樂, 曹志強, 等. 基于模糊控制協調策略的多自主機器人圍捕[J]. 華中科技大學學報: 自然科學版, 2011, 39(S2): 328-331. YUAN Yuan, JIAO Jile, CAO Zhiqiang, et al. Fuzzy control coordination based hunting of multiple autonomous robots[J]. Journal of Huazhong university of science and technology: natural science edition, 2011, 39(S2): 328-331.

[11]王雪松, 高陽, 程玉虎, 等. 知識引導遺傳算法實現機器人路徑規劃[J]. 控制與決策, 2009, 24(7): 1043-1049. WANG Xuesong, GAO Yang, CHENG Yuhu, et al. Knowledge-guided genetic algorithm for path planning of robot[J]. Control and decision, 2009, 24(7): 1043-1049.

[12]DEFOORT M, FLOQUET T, KOKOSY A, et al. Sliding-mode formation control for cooperative autonomous mobile robots[J]. IEEE transactions on industrial electronics, 2008, 55(11): 3944-3953.

錢殿偉，男，1980年生，副教授，博士，主要研究方向為變結構控制理論與應用、智能機器人技術、欠驅動機器人控制。

Formation control of multi-robot systems in a fuzzy sliding mode

QIAN Dianwei

(School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China)

To resolve the formation problem resulting from a swarm of robots, a control scheme is proposed based on sliding mode control and fuzzy logic. A formation dynamic model is established utilizing the leader-follower approach. The model is subject to uncertainties. If the upper bounds of these uncertainties are unknown, then a fuzzy compensator can be adopted to approximate the uncertainties. From an Lyapunov approach, not only is the sliding-mode-based formation control system asymptotically stable, but the approximate error of the fuzzy compensator is also convergent. The simulation results demonstrate that the robots can rapidly form and maintain the desired specified geometrical shapes during movement.

multi-robot; formation control; uncertainties; sliding model control; fuzzy logic

2015-10-22.

日期：2016-08-24.

國家自然科學基金項目(60904008).

錢殿偉.E-mail：dianwei.qian@ncepu.edu.cn.

TP242.6

A

1673-4785(2016)05-0641-07

10.11992/tis.201510017

http://www.cnki.net/kcms/detail/23.1538.TP.20160824.0929.008.html

錢殿偉.基于模糊滑模的多機器人系統編隊控制[J]. 智能系統學報， 2016, 11(5):641-647.

英文引用格式：QIAN Dianwei.Formation control of multi-robot systems in a fuzzy sliding mode [J]. CAAI transactions on intelligent systems, 2016,11(5):641-647.