關于套利組合最大收益問題的求解

毛克寧 林芳 王煒 魏嫚

摘要：本文從兩個方面論述了套利組合最大收益問題的求解。一是對于一些簡單情形直接用線性代數(shù)方法求解，分析和給出了這些情形下的某些結論。二是對于一般情形通過建立線性規(guī)劃模型求解，并使得運算簡化。

關鍵詞：套利組合 最大收益 分析 求解

一、套利組合最大收益簡單情形的求解

（一）概念與例的分析

分別用[xj]、[βji]和[E（rj）]表示按市值計算的投資者對證券[j]持有量的改變量、證券[j]的收益率對因素[i]的敏感度和證券[j]的期望收益率。套利組合滿足以下三個條件：

[j=1nxj=0]，（2）[j=1nβjixj=0 （ i=1， 2， …， s）]，單因素模型為[j=1nβjxj=0]，[j=1nxjE（rj）>0]。

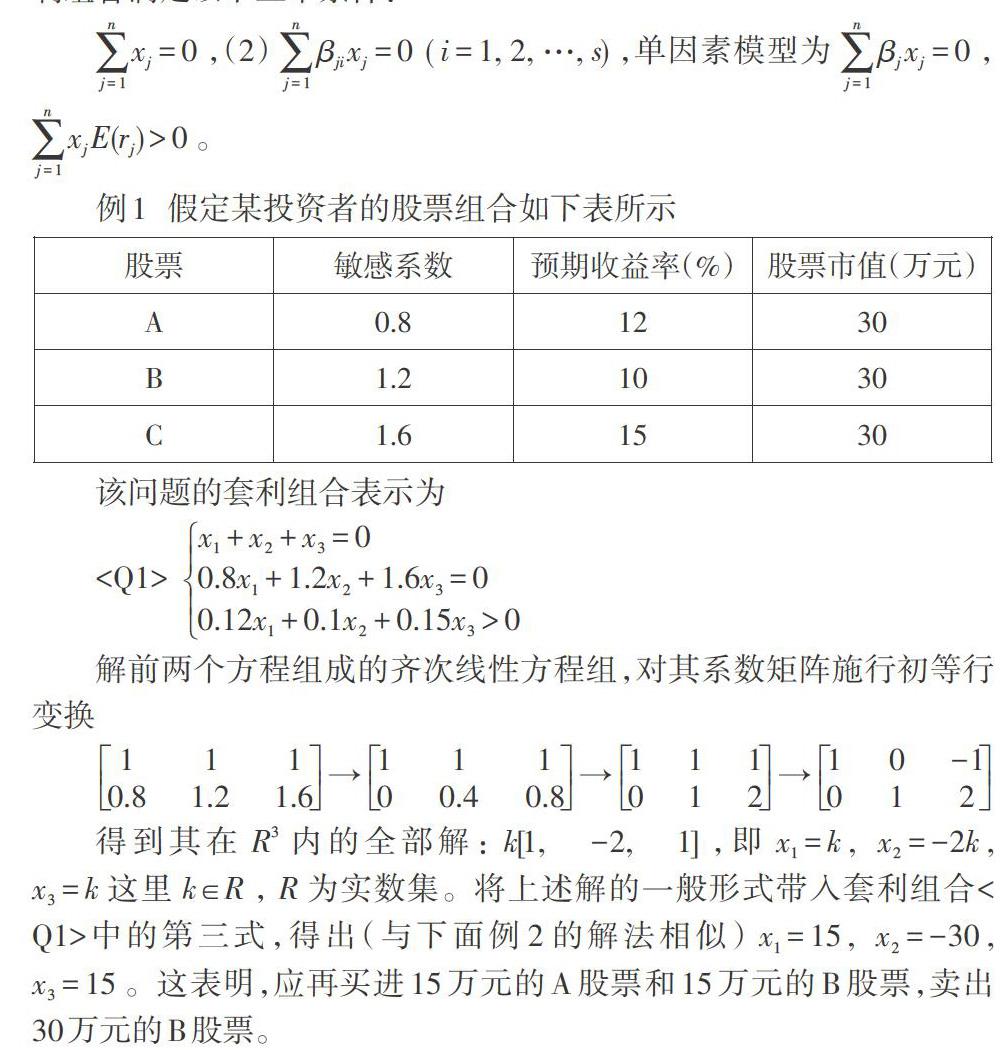
例1 假定某投資者的股票組合如下表所示

該問題的套利組合表示為

解前兩個方程組成的齊次線性方程組，對其系數(shù)矩陣施行初等行變換

[1110.81.21.6→11100.40.8→111012→10-1012]

得到其在[R3]內的全部解：[k[1，-2，1]]，即[x1=k]， [x2=-2k]， [x3=k]這里[k∈R]，[R]為實數(shù)集。將上述解的一般形式帶入套利組合中的第三式，得出（與下面例2的解法相似）[x1=15]， [x2=-30]， [x3=15]。這表明，應再買進15萬元的A股票和15萬元的B股票，賣出30萬元的B股票。

從該例看出，對于單因素套利模型，并非期望收益率最高的股票買進增量越大越好。在該例中，為獲得套利組合的最大收益，并非將A股票和B股票全部賣掉后全部買進期望收益率最高的C股票。事實上，若將A股票和B股票全部賣掉而全部買進C股票，則有[x1=-30]， [x2=-30]， [x3=60]。這不滿足中的第二個方程，說明這樣不符合套利組合不承擔因素風險的要求。那么，對于單因素套利模型，為使得套利組合的收益最大，是否一定要將期望收益率最低的股票全部賣掉呢？看下面一個與例1略有不同的例子。

例2 假定某投資者的股票組合如下表所示

[股票＼&敏感系數(shù)＼&預期收益率

解前兩個方程組成的齊次線性方程組（與例1完全相同），得到其在[R3]內的全部解：[k[1，-2，1]]，即[x1=k]， [x2=-2k]， [x3=k] 這里[k∈R]，[R]為實數(shù)集。將上述解的一般形式帶入套利組合中的第三式，有[0.15k-0.24k+0.1k>0]，即[0.01k>0]，因此，[k>0].要使得套利組合的預期收益最大，就是要使[0.01k]最大（[k>0]），于是[k]應盡可能地大；由于原有30萬元B股票，故[-2k≤30]，即[k≤15] 因此，要使得套利組合的預期收益最大，應取[k=15]，即[x1=15]， [x2=-30]， [x3=15]。這表明，應賣出30萬元的B股票，再買進15萬元的A股票和15萬元的B股票。

該例中全部賣掉的不是期望收益率最低的C股票，而是期望收益率居中的B股票。事實上，若將C股票全部賣掉，即[x3=-30] 于是中前兩個方程分別變?yōu)閇x1+x2=30]與[0.8x1+1.2x2=1.6×30]。聯(lián)立這兩個方程，解得[x1=-30]， [x2=60]。但這會使得中最后一個不等式的左邊小于零，說明預期是賠本的。這是因為若將C股票全部賣掉，引起A股票和B股票的相應變動，而這三只股票的變動要符合套利組合的前兩個條件。于是必須再將A股票全部賣掉，并將賣掉A股票和C股票的全部資金都用來購買B股票。但由于B股票的期望收益率低于C股票的期望收益率較多，造成虧損。

以上兩例對于為什么不一定要賣掉其他股票而全部購買期望收益率最高的股票或賣掉期望收益率最低的股票去買其他股票的分析，對于考慮交易費用的情形也是有意義的。

例1和例2都屬于單因素套利模型的例子，對于一些簡單的雙因素套利模型仍可用類似的解法，這里不再贅述。注意到在例1的和例2的中，各自前兩個方程組成的齊次線性方程組的未知量個數(shù)與其系數(shù)矩陣的秩之差都等于1，也即只有1個自由未知量，用上述線性代數(shù)方法可以求解套利組合的最大收益問題。但對于單因素或多因素模型組成的齊次線性方程組中未知量個數(shù)與其系數(shù)矩陣的秩之差都≥2，也即自由未知量個數(shù)≥2的情形，尤其在考慮交易費用情況下直接用線性代數(shù)方法求解套利組合的最大收益問題會有很多麻煩。

（二）兩只股票的單因素套利

假定某投資者擁有兩只股票[A]與[B]，[xA]與[xB]分別表示按市值計算的投資者對這兩只股票持有量的改變量；[βA]與[βB]分別表示股票[A]與股票[B]的收益率對宏觀因素的敏感度；[E（rA）]與[E（rB）]分別表示股票[A]與[B]的期望收益率。按照定義，套利組合必須滿足以下部分條件：

[xA+xB=0βAxA+βBxB=0]

這一齊次線性方程組的系數(shù)行列式為[D=11βAβB=βB-βA]

若[βA≠βB]，則[D≠0]，于是只有零解，即[xA=xB=0]。這說明不應改變股票[A]與股票[B]的原持有量。因此，如果投資者僅擁有的兩只股票的收益率對宏觀因素的敏感度不同，則無套利機會。這是因為套利組合不承擔因素風險，即[βAxA+βBxB=0]，由于[xA+xB=0]這一零和性，使得[xB=-xA]，于是有[βAxA-βBxA=0]，即[βAxA=βBxA]；若[xA≠0]（從而[xB≠0]）， 則有[βA=βB]。 因此，若[βA≠βB]，必然[xA=xB=0]，即無套利機會。

分別以[pA（≥0）]，[pB（≥0）]和[mA（≥0）]，[mB（≥0）]表示股票[A]與[B]按市值計算的買進數(shù)量和賣出數(shù)量，于是[xA=pA-mA]，[xB=pB-mB]；分別以[aA（≥0）]，[aB（≥0）]和[bA（≥0）]，[bB（≥0）]表示買進和賣出股票[A]與[B]的交易費率，則這兩只股票的單因素套利模型為

[xA+xB=0βAxA+βBxB=0E（rA）xA+E（rB）xB-（aApA+aBpB）-（bAmA+bBmB）>0]

若[βA=βB]，則有

[xA+xB=0 ……①E（rA）xA+E（rB）xB>（aApA+aBpB）+（bAmA+bBmB） ……② ]

由①得[xB=-xA]，將其代入②，有[（E（rA）-E（rB））xA>（aApA+aBpB）+（bAmA+bBmB） ]

若[E（rA）=E（rB）]，則有[0>（aApA+aBpB）+（bAmA+bBmB）]，但這顯然是不可能的。因此，當[E（rA）=E（rB）]時，無套利機會。這在常識上不難理解：因為，若一個投資者僅持有兩只股票，這兩只股票的期望收益率相同并且對宏觀因素的敏感度相同，則無需變動這兩只股票的原持有量，即使變動也無法增加收益，而且在有交易費用的情況下，還會白白損失交易費用。這也說明了套利組合模型與“常識”是相吻合的。

由上面分析看出：若[E（rA）≠E（rB）]并且[βA=βB]，則

當[xA]與[xB]正負相反，且[xA=xB>（aApA+aBpB）+（bAmA+bBmB）（E（rA）-E（rB）] 時，就實現(xiàn)了套利。

特別地，在不考慮交易費用的情況下，即當[aA=aB=bA=bB=0]時，不難看出：若[E（rA）>E（rB）]（[βA=βB]），取[xA=yB]，[xB=-yB]（這里[yB]表示股票B按市值計算的原持有量），則可以獲得最大套利收益；[E（rB）>E（rA）]的情況類似。

二、套利組合最大收益一般情形的求解

現(xiàn)在考慮一般情況下套利組合的最大收益問題。假設投資者原有的[n]只股票按市值計算的持有量分別為[y1（>0）， y2（>0）， …， yn（>0）]，它們的改變量分別為[x1，x2，…，xn]；這[n ]只股票改變后按市值計算的持有量分別為[z1，z2，…，zn]，即[zj=xj+yj] （[j=1， 2，…， n]）。以[pj]和[mj]分別表示股票[j]按市值計算的買進數(shù)量和賣出數(shù)量。這樣，投資者按市值計算的對股票[j]持有量的改變量[xj]可表示為[xj=pj-mj]。分別以[aj（>0）]和[bj（>0）]表示買進和賣出股票[j]的交易費率（[j=1， 2，…， n]）。考慮交易費用的套利組合最大收益問題，可表示為線性規(guī)劃模型LP：

[maxj=1n（pj-mj）E（rj）-j=1najpj-j=1nbjmj[6]]

[ j=1n（pj-mj）=0j=1nβji（pj-mj）=0 （i=1， 2，…， s）j=1n（pj-mj）E（rj）-j=1najpj-j=1nbjmj≥0 [7]mj≤yj pj≥0， mj≥0（j=1， 2， …，n）]

在參考文獻[5]中，所舉的例子屬于單因素套利模型，為了使問題更具有一般性，下面考慮一個較為復雜的多因素套利模型的例子：

例3 假定某投資者擁有七只股票，情況如下表

[股票＼&敏感系數(shù)βj1＼&敏感系數(shù)βj2＼&敏感系數(shù)βj3＼&預期收益率（%）＼&股票市值

這里引用一個參考文獻[5]中的命題：將本文的線性規(guī)劃模型LP中原標有上標的約束去掉后相應的線性規(guī)劃模型記作LP。若LP有最優(yōu)解，并且其目標函數(shù)最優(yōu)值大于原標有上標的約束的不等式右端項，則LP的最優(yōu)解也是LP的最優(yōu)解，并且最優(yōu)值不變。根據(jù)上述命題，LP的最優(yōu)解存在且與LP的最優(yōu)解相同，這可以通過LINDO軟件的計算得以驗證。

參考文獻：

[1]賴家元，周文.證券投資學[M].華中科技大學出版社，2007

[2]北京大學數(shù)學力學系幾何與代數(shù)小組，高等代數(shù)[M].高等教育出版社，1978

[3]薛嘉慶.線性規(guī)劃[M].高等教育出版社，1989

[4]胡運權.運籌學教程[M].清華大學出版社，2012

[5]毛克寧.套利組合的最大收益模型研究[J].數(shù)學的實踐與認識，2016，5，133-139

[6]謝金星，薛毅.優(yōu)化建模與LINDO/LINGO軟件[M].清華大學出版社，2005

[7]李晶瑩，劉金蘭.考慮交易成本的套利組合研究[J].中國管理科學，2002，10（專輯）：229-232