周向缺陷位置對彎管承載能力的影響

萬 晉 秦 超

(福州大學石油化工學院)

周向缺陷位置對彎管承載能力的影響

萬 晉*秦 超

(福州大學石油化工學院)

以彎管為研究對象，采用有限元法對彎管中間橫截面應力分布規律和塑性極限載荷進行研究，給出了彎管在內壓和彎矩載荷下的應力分布情況，指出了彎矩載荷下彎管中間截面最大軸向應力點位置和計算公式，分析了中間截面上不同位置周向裂紋缺陷對彎管塑性極限彎矩載荷的影響。結果表明，對于彎曲半徑比較小，徑厚比較大的彎管應將周向裂紋缺陷定位在最大軸向應力點確定彎管彎矩承載能力，為進一步研究彎管塑性極限彎矩，完善彎管失效評定奠定基礎。

彎管 周向裂紋 塑性極限彎矩 失效評定

彎管是壓力管道中重要的元件之一，在用于管路改向的同時，作為彈性元件可通過彈性或塑性變形吸收系統中由于熱膨脹等因素產生的力和力矩，在復雜載荷作用下彎管成為管系中高應力部位[1]，若彎管中存在原始或使用中產生的缺陷，是否會危及管道的安全運行已成為工程技術人員關注的問題，而我國現行的GB/T 19624-2004[2]對管道缺陷的評定方法僅適用于直管段，且未給出對于各類管件以及管件與直管連接區域的缺陷安全性評定的適用性和具體要求。

含裂紋管道的安全評定需要使用結構的塑性極限載荷值，對于無缺陷彎管的塑性極限載荷前人已經做了大量的工作[3～8]。對于含周向面型缺陷的彎管塑性極限載荷，在內壓作用下，彎管軸向應力與直管一致，可用直管的凈截面失效準則求得；在彎矩載荷下，因彎管的變形性狀與直管差距較大，其塑性極限彎矩成為進一步完善管道失效評定的一個重要課題之一。近年來，對于彎管塑性極限載荷的研究也主要集中在塑性極限彎矩和塑性極限聯合載荷，由于石油化工等行業管道的特殊性，研究重點是表面裂紋，Griffiths J E用試驗的方法研究了缺陷尺寸對彎管塑性極限彎矩的影響[4]；Yahiaoui K等利用有限元法對含周向表面裂紋塑性極限載荷影響因素進行了研究，并結合實驗對模擬的可靠性進行了驗證[9～12]；Kim Y J等通過有限元模擬結果給出含周向面型缺陷彎管塑性極限彎矩的擬合公式，并且進一步對聯合載荷及與彎管相連直管對彎管的影響做了詳細研究[13～15]。

1 彎管應力研究

直管塑性極限載荷主要與管道材料、直徑、厚度、裂紋尺寸和位置相關，而彎管還受彎曲半徑影響。對于含周向面型缺陷彎管塑性極限載荷的研究，首要問題是分析彎管應力分布規律，考慮到按照裂紋的力學特征劃分的張開型、滑開型和撕開型3種裂紋中，以張開型裂紋危險性最大，也最為常見，成為斷裂力學研究的重點，對于沿彎管橫截面的周向面型缺陷，其應力研究也將重點集中在軸向應力的分布。

1.1計算模型和模擬結果驗證

由于彎管中心線存在曲率，在承受彎矩載荷時力學性能和直管存在很大不同。筆者應用結構有限元ANSYS軟件，建立彎頭與直管連接結構的三維有限元模型，模型尺寸參量如圖1所示，為避免模型邊界約束對分析區域計算結果的影響以及實際使用中彎管通常與直管相連，故模型中取直管長度L=5D[10]，彎頭及其與直管連接面邊緣區域采用20節點的SOLID186單元，遠離邊緣區的直管段用8節點的SOLID185單元，并在彎管及與直管連接邊緣區域形成較為致密的單元，在保證計算精度的同時節省計算時間，以結構軸向平面為對稱面，建立結構的1/2模型(圖2)，在對稱面施加對稱約束，在模型內表面施加均勻分布的面力模擬內壓載荷，在直管的一個自由端添加MASS21質點單元模擬彎矩載荷，以達到模擬結構受載狀況。

圖1 管道結構參量示意圖

圖2 有限元計算模型

為了驗證上述計算模型的正確性和可靠程度，選用彎曲半徑比R/D=1.5、徑厚比r/t=10(λ=0.3145)的彎管作為驗證模型，提取彎管中間截面的外表面應力分布，將ASME Ⅲ NB-3865中提供的彎管中間截面應力計算公式與模擬計算結果進行比較，在1MPa內壓和1kN·m開彎載荷分別作用下該截面應力模擬結果和ASME公式計算結果比對如圖3所示，可以看出在兩種載荷情況下周向和軸向的應力在大小、趨勢方面均有很好的契合度，從而驗證了有限元計算所采用的模型是正確的，所計算的結果將是可信的。

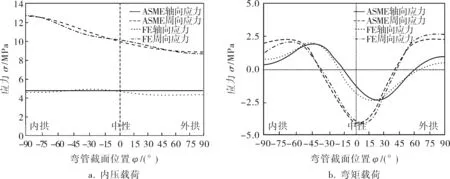
圖3 有限元法與ASME公式計算結果對比

1.2彎矩載荷作用下應力分布

用有限元法分別計算M=±1kN·m的閉彎和開彎載荷作用下，r/t=30、R/D=1.0的彎頭與直管連接結構應力，并提取內、外拱線和中性線3個路徑軸向應力σθM(圖4)，可見各路徑上兩種彎矩所產生的軸向應力分布曲線各自對稱于橫坐標，在內、外拱線處軸向應力大小相等，方向相反；在彎矩作用下彎頭中性線的軸向應力絕對值遠高于內、外拱線處，說明彎頭的受力與直管有本質的不同，不能象直管以等彎矩的空心梁來看待。在閉彎載荷作用下，彎頭絕大部分區域承受軸向拉應力，只有靠近內拱線較小的范圍內承受較小的壓應力，而承受開彎載荷時應力分布剛好相反，由此可以推論閉彎載荷的大小對彎頭的強度影響較大，而開彎較易產生結構失穩破壞。從應力分布曲線可以得出在純彎矩作用下，彎管中間橫截面(θ=45°)中性線處應力最大，是最危險截面。

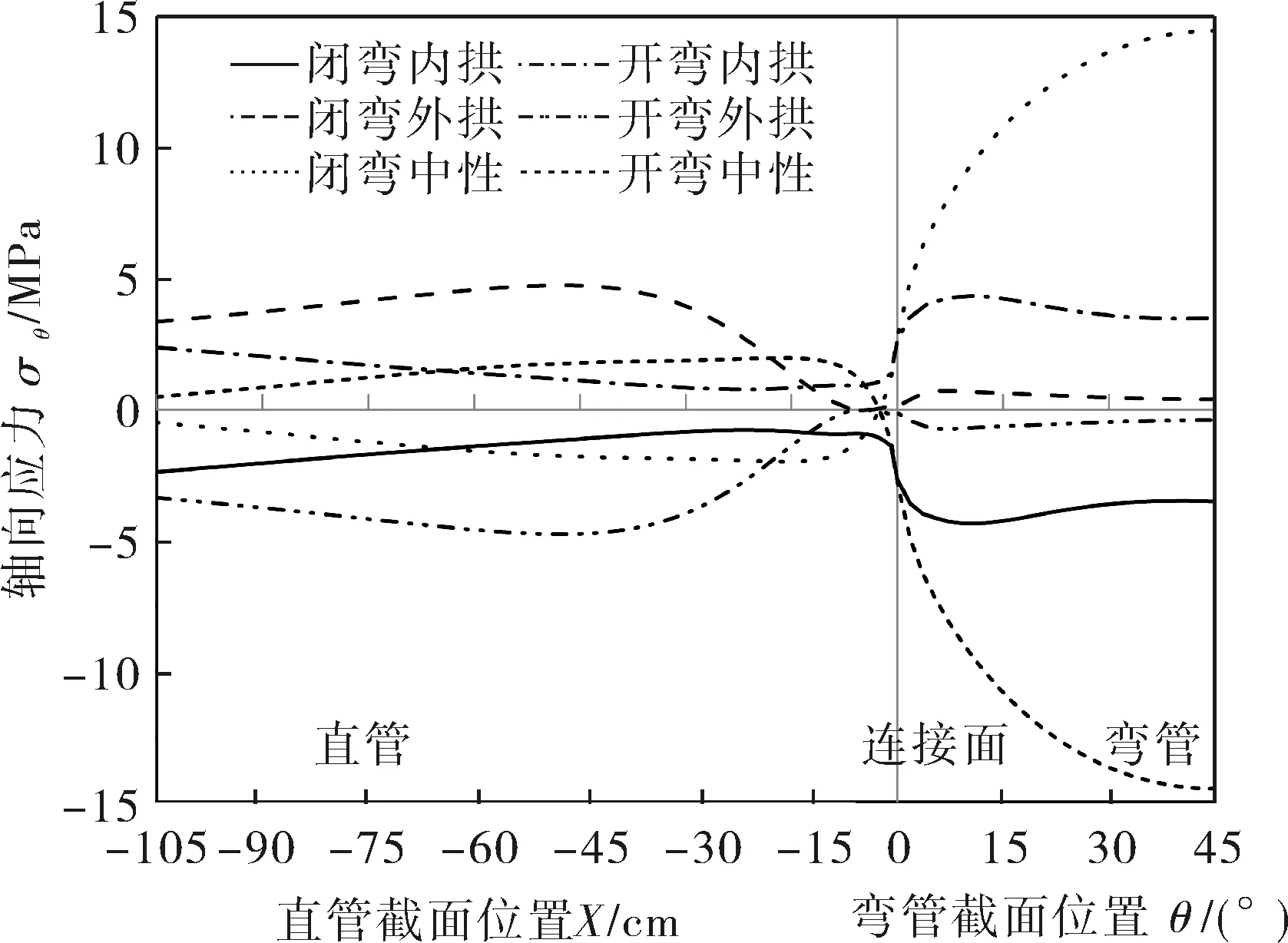
圖4 彎矩作用下結構外壁面3條路徑軸向應力分布

為了便于研究軸向應力最大的中間橫截面存在周向裂紋的彎管塑性極限載荷分布規律，以同幾何參數的直管在彎矩載荷作用下的軸向應力σM=M/(πr2t)為基準，對彎管中間橫截面軸向應力進行歸一化處理，從而得到如圖5所示在開、閉彎載荷各自作用下彎管中間面上的軸向應力分布集中系數Kφ的狀況，可以看出，兩種彎矩載荷在內外壁產生的軸向應力曲線對稱于圖中的橫坐標，同時兩種載荷條件下厚壁彎管和薄壁彎管的最大軸向應力都是發生在外壁；值得注意的是只有當壁厚較大時，在開彎載荷作用下，彎管表現的應力分布規律和直管相近，最大軸向應力位于拱線位置，中性軸應力較小，但是隨著壁厚的減少，r/t值增大，在彎矩作用下彎管表現出來的力學性能和直管有明顯的區別，中間橫截面上軸向應力值為零的點并不在彎管的中性線處，并且最大軸向應力也不是發生在內、外拱線位置，尤其是對于薄壁管道在閉彎載荷條件下，彎管中間截面應力分布規律與直管完全不同，最大軸向應力總是出現在中性線附近，靠近外拱線一側；當彎矩大小相同時，閉彎在連接面上所產生最大軸向拉應力值略大于開彎，該點與中性線有12°夾角。

圖5 彎矩作用下彎管中間橫截面軸向應力集中系數分布

1.3應力分布規律研究

為了研究應力分布與結構幾何尺寸之間的關系，分別計算了工程中常見的R/D=1.0～3.0、r/t=5～40范圍內的彎頭與直管連接結構，提取彎管中間截面應力分布，找出彎矩載荷下最大拉應力位置，得到彎管中間截面軸向應力分布提取最大應力位置見表1。

借助OriginPro數據分析軟件擬合整理，得到彎矩載荷下連接面最大軸向拉應力位置φmax的計算式：

(1)

表1 最大應力出現的位置φmax

通過比較可以看到對于薄壁管道(r/t≥10)擬合公式得到的最大軸向應力位置具有很好的準確度，可以作為彎管計算塑性極限彎矩時確定發生周向缺陷的最危險位置的依據。

2 彎管塑性極限載荷研究

確定含周向裂紋直管塑性失穩失效準則主要有凈截面垮塌準則、韌帶斷裂應力準則、半經驗極限載荷準則、經驗下界極限載荷式和局部失穩經驗公式，其中Kanninen M F等提出的凈截面垮塌準則以其概念明確、形式簡單而得以廣泛應用，并成為國際上各主要缺陷評定規范中含周向缺陷壓力管道極限載荷計算的主要方法[16]，在進行安全評定的時候，不具體考慮實際缺陷在截面中的具體位置，認定其處于截面中最危險點，計算得到塑性極限載荷，從而簡化安全評定方法并保證失效評定結果的安全性，因此對于彎管進行安全性分析也應選擇最危險情況下塑性極限載荷進行評定。考慮到石化管道的特殊性，含周向表面裂紋管道塑性極限載荷是研究的重點，前人對于彎管含周向裂紋塑性極限彎矩都有不同程度的研究，值得注意的是他們在研究過程中對于周向裂紋位置的選擇，均按照直管表現出來的力學性能進行選擇，即將周向裂紋位置定在內、外拱線位置。根據前面的分析，彎管的R/D較小，r/t較大時其最危險點并不在內、外拱線處，導致其所得的結果比較適用于大彎曲半徑的厚壁彎管，而對于工程中常用的大多采用沖壓或推彎工藝加工的彎頭，彎曲半徑較小，具有明顯的局限性。

2.1含周向裂紋管道模型建立和驗證

分析極限載荷需要借助結構的載荷-變形曲線來完成，其中的變形參量的選取是非常重要的。JB 4732-2005[17]和ASME規范[7]都規定，確定結構極限載荷點的變形或者應變時應能反映結構的承載能力。筆者選擇彎管的最大主應變點作為控制點，繪制載荷與最大主應變間的關系曲線確定極限載荷。在應用有限元進行極限分析時，假設彎管為理想彈塑性材料，為了滿足有限元計算要求，假設材料有微弱的強化，采用雙線性隨動塑性強化模式。為了驗證有限元模擬的準確性，選擇和文獻[10]相同的管道和材料參量，對彎管塑性極限載荷進行研究。計算模型彎頭中徑D=83.41mm、厚度t=5.49mm、彎曲半徑R=76mm,材料彈性模量E=210GPa，泊松比μ=0.3，理想彈塑性材料的屈服強度取實際材料的流變應力σf=(σy+σu)/2=404MPa，得到含周向裂紋彎管最大主應變點處載荷與主應變曲線如圖6所示，并采用比較保守的2倍斜率法[17]得到結構塑性極限彎矩，本文的有限元數值解與文獻中的實驗值的最大誤差為0.99%，且略偏于保守，證明所建立的模型較為精確，能準確地反映彎管承受彎矩載荷時實際情況。

2.2裂紋位置對彎管塑性極限彎矩影響

根據彎管應力分布研究，小彎曲半徑薄壁彎管由于中心線存在曲率半徑，其中間截面在彎矩載荷作用下表現出與直管完全不同的力學性能，不能簡單看作等截面空心梁，在彎矩作用下結構其最危險點不在內、外拱線處；在研究彎管塑性極限載荷時，若將裂紋缺陷位置選在內、外拱線處，并將所得的塑性極限載荷作為含裂紋缺陷彎頭結構最小極限載荷有可能高估了其承載荷能力，是不適宜的。為了研究裂紋所處位置對于彎管塑性極限載荷的影響，選取彎矩載荷作用下，以彎頭R/D=1.0和徑厚比r/t=3～15的管道作為研究對象，計算得到裂紋處在不同位置時彎管塑性極限載荷，并與裂紋處在拱線位置的極限載荷相比，得到在閉彎和開彎載荷作用下的比值系數kφc=Mφc/MCc和kφo=Mφo/MAo，由圖7可看出：雖然存在相同大小周向裂紋的彎管，極限承載能力隨裂紋所處位置不同而發生變化，同時也表明將裂紋選在拱線位置，同時作為彎管結構最危險位置，可能高估含裂紋缺陷彎頭的承載能力，尤其是對于閉彎載荷高估的程度更大。

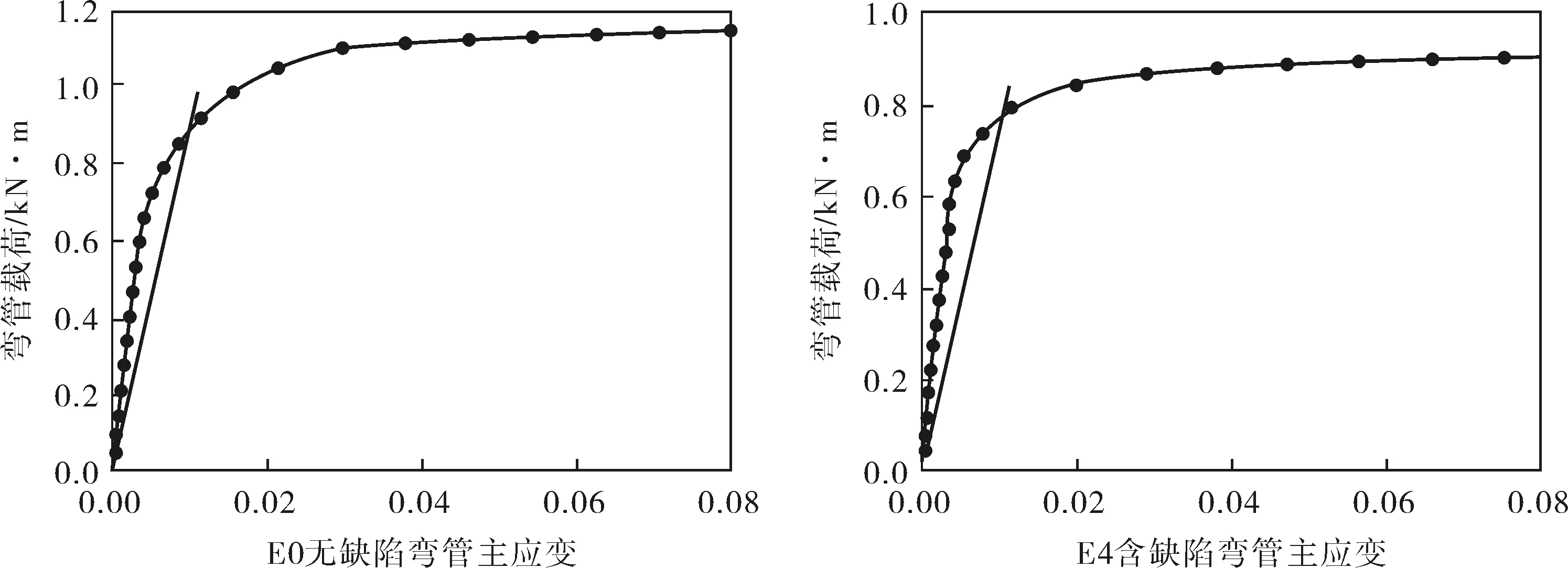
圖6 控制點載荷與主應變曲線

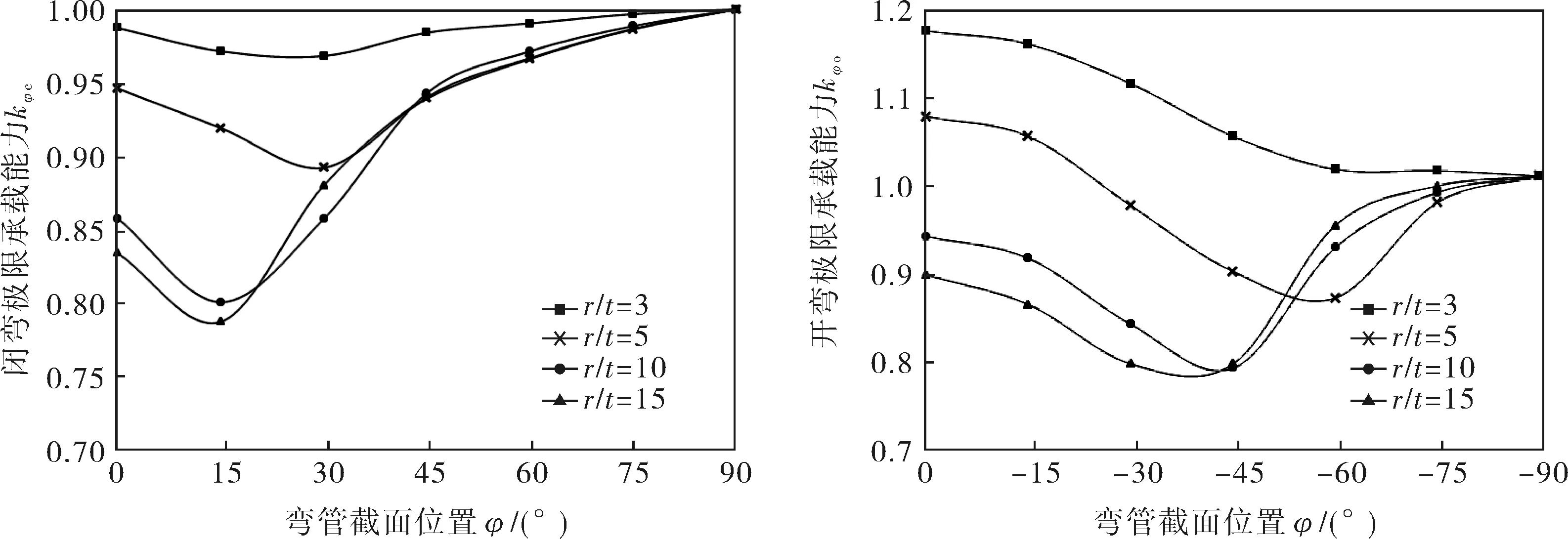
圖7 裂紋位置對極限承載能力的影響

在閉彎載荷作用下，周向裂紋位于彎管中性線附近偏外拱線一側是比較危險的，并且徑厚比越大，彎管承載能力削弱程度也越大，在r/t=15，裂紋在φ=15°位置時承載能力比裂紋在外拱線位置時降低了21.4%；在開彎載荷作用下，周向裂紋處在中性線附近偏內拱線一側危險性較大，當r/t=15時最大削弱程度也達到了20%。由圖7可以得出隨著徑厚比的增大，裂紋所處位置對彎矩承載能力的影響越大，當彎頭的r/t≥5，Yahiaoui K將拱線處存在周向裂紋的彎頭彎矩承載能力作為安全性評定的基準是極其危險的。

通過圖7的曲線分布可以發現，當周向裂紋位于最大軸向應力位置時，彎管極限承載能力最低，所以在確定彎管塑性極限彎矩載荷，并作為結構極限承載能力時，應充分考慮彎管中間橫截面應力分布規律，將周向裂紋選在最大軸向應力位置，即由式(1)計算確定周向裂紋位置。

盡管彎管力學性能和直管不同，但是隨著彎曲半徑的增大，在彎矩載荷作用下的應力分布將逐漸趨近于直管，為了研究不同的彎曲半徑比情況下，缺陷處在最危險位置時對彎管塑性極限彎矩的影響，建立彎曲半徑比R/D=1.0～5.0的彎管模型，計算得到裂紋位于最大軸向應力位置塑性極限彎矩，并將它與裂紋處于拱線位置塑性極限彎矩進行比較，得到彎管的塑性極限彎矩降低系數Kro和Krc，由圖8可知，隨著彎曲半徑的增大，彎管應力分布規律趨近于直管，最危險裂紋位置處塑性極限載荷相較于裂紋位于內外拱線位置削弱程度不斷降低；隨著厚度的增大，這種削弱程度也不斷減弱。對于閉彎載荷，徑厚比r/t=5的彎管在彎曲半徑比R/D=5.0的情況下削弱系數為零，當裂紋位于外拱線位置時彎管塑性載荷最低；而開彎在彎曲半徑比R/D=5.0的情況下最危險裂紋位置都在內拱線位置。工程中通常使用的沖壓或推彎的彎頭R/D值較小，通常小于3.0，此時無論是開彎還是閉彎載荷，確定彎頭的極限彎矩承載能力均應將缺陷位置放在應力最大點，因為此時得到的極限彎矩才是結構的最小承載能力，而彎矩載荷下彎頭的最大應力點可以用式(1)計算確定。

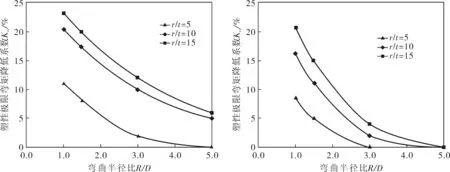
圖8 不同彎曲半徑塑性極限載荷降低情況

3 結束語

分析各種彎曲半徑比和徑厚比的彎頭模擬計算結果得出：小彎曲半徑薄壁彎管在彎矩載荷作用下表現出和直管完全不同的應力分布特性，給出了確定彎管最大應力點的計算公式。在對彎管軸向應力詳細研究的基礎上，對存在周向裂紋彎管，分析裂紋處在不同位置時的塑性極限彎矩變化情況，得出彎管不能簡單的與直管等同看待，將裂紋定位在內外拱線計算得到的塑性彎矩極限載荷有可能不是結構的最小承載能力，尤其是R/D較小，而r/t較大時反映得越明顯。

[1] 舒安慶, 劉小麗, 魏化中.含點蝕缺陷燃氣彎管塑性極限載荷分析[J].化工機械, 2009, 36(1): 22～24.

[2] GB/T 19624-2004, 在用含缺陷壓力容器安全評定[S].北京：中國標準出版社, 2004.

[3] 潘家華, 郭光臣, 高錫祺. 油罐及管道強度設計 [M]. 北京：石油工業出版社, 1986.

[4] Griffiths J E. The Effect of Cracks on the Limit Load of Pipe Bends under In-plane Bending: Experimental Study [J]. International Journal of Mechanical Sciences, 1979, 21(2): 119～130.

[5] Calladine C R. Limit Analysis of Curved Tubes [J]. Journal of Mechanical Engineering Science, 1974, 16(2): 85～92.

[6] Shalaby M A, Younan M Y A. Limit Loads for Pipe Elbows with Internal Pressure under In-plane Closing Bending Moments[C].The Proceedings of the 1997 ASME Pressure Vessels and Piping Conference.SanDiego:ASME,1998:163～170.

[7] ASME Boiler and Pressure Vessel Code Section III, Division 1, Nuclear Power Plant Components[S] .New York:ASEM, 2013.

[8] 段志祥, 石坤, 沈士明. 面外彎矩作用下彎頭極限載荷有限元分析[J].化工機械, 2012, 39(5): 614～617.

[9] Yahiaoui K, Moffat D, Moreton D. Piping Elbows with Cracks Part 1: A Parametric Study of the Influence of Crack Size on Limit Loads Due to Pressure and Opening Bending [J]. The Journal of Strain Analysis for Engineering Design, 2000, 35(1): 35～46.

[10] Yahiaoui K, Moffat D, Moreton D. Piping Elbows with Cracks Part 2: Global Finite Element and Experimental Plastic Loads under Opening Bending [J]. The Journal of Strain Analysis for Engineering Design, 2000, 35(1): 47～57.

[11] Hong S P, Kim J H, Kim Y J, et al. Effect of Internal Pressure on Plastic Loads of 90 Elbows with Circumferential Part-Through Surface Cracks under in-plane Bending [J]. Engineering Fracture Mechanics, 2010, 77(4): 577～596.

[12] Hong S P, Kim J H, Kim Y J. Limit Pressures of 90 Elbows with Circumferential Surface Cracks [J]. Engineering Fracture Mechanics, 2009, 76(14): 2202～2216.

[13] Kim Y J, Kim Y I, Song T K. Finite Element Plastic Loads for Circumferential Cracked Pipe Bends under In-plane Bending [J]. Engineering Fracture Mechanics, 2007, 74(5): 643～668.

[14] Kim Y J, Oh C S. Closed-form Plastic Collapse Loads of Pipe Bends under Combined Pressure and In-plane Bending [J]. Engineering Fracture Mechanics, 2006, 73(11): 1437～1454.

[15] Kim Y J, Oh C S. Effects of Attached Straight Pipes on Finite Element Limit Analysis for Pipe Bends [J]. International Journal of Pressure Vessels and Piping, 2007, 84(3): 177～184.

[16] Kanninen M F, Broek D, Hahn G T, et al. Towards an Elastic-Plastic Fracture Mechanics Predictive Capability for Reactor Piping [J]. Nuclear Engineering and Design, 1978, 48(1): 117～134.

[17] JB 4732-2005, 鋼制壓力容器-分析設計標準[S].北京:技術標準出版社, 2005.

PositionEffectofCircumferentialCrackDefectsonElbowPipeBearingCapacity

WAN Jing,QIN Chao

(SchoolofChemicalEngineering,FuzhouUniversity,Fuzhou350108,China)

Taking elbow pipe as the object of study, the finite element method was adopted to investigate axial stress distribution on the cross section of the elbow pipe and plastic limit load; and the stress distribution there under internal pressure and bending load was summarized, including location of the maximum axial stress and its calculation formulation. Analyzing the position effect of circumferential crack defects on the elbow pipe’s bearing capacity shows that, as for the elbow pipe with smaller bending radius and bigger diameter-thickness ratio, the circumferential crack defect should be located at the spot of the maximal axial stress so as to determine the elbow’s bearing capacity and lay the foundation for further study of the plastic ultimate bending moment and improvement of elbow failure assessment.

elbow, circumferential crack, plastic limit bending moment, failure assessment

*萬 晉，男，1957年7月生，副教授。福建省福州市，350108。

TQ055.8+1

A

0254-6094(2016)03-0390-07

2015-11-17，

2015-12-06)