部分穿孔管消聲器聲學(xué)性能有限元分析
溫逸云,鄧兆祥,張 楊
(重慶大學(xué) 汽車工程學(xué)院,重慶 400044)
部分穿孔管消聲器聲學(xué)性能有限元分析
溫逸云,鄧兆祥,張 楊
(重慶大學(xué) 汽車工程學(xué)院,重慶 400044)
穿孔管消聲器因具有良好的聲學(xué)性能和較低的壓力損失而被運用于消除內(nèi)燃機排氣噪聲。通過運用有限元法研究部分穿孔消聲器穿孔率、插入長度、周向和軸向穿孔分布、擴張腔直徑等設(shè)計參數(shù)對消聲器消聲性能的影響。得到如下結(jié)論:穿孔率增大、插入長度變短會引起低頻共振峰向高頻方向偏移;穿孔率增大、擴張腔直徑減小都會引起有效消聲頻率范圍的拓寬;穿孔的軸向、周向分布對消聲器消聲性能沒有影響。
聲學(xué);傳遞損失;消聲性能;部分穿孔消聲器;有限元法;結(jié)構(gòu)參數(shù)
穿孔結(jié)構(gòu)由于其低阻力等許多優(yōu)良的性能,因而被廣泛應(yīng)用在消聲器的設(shè)計中[1],近年來也有許多學(xué)者從事其相關(guān)研究工作,季振林曾用一維解析法和三維子結(jié)構(gòu)邊界元法預(yù)測單腔直通穿孔管消聲器的傳遞損失,也對部分穿孔(管道內(nèi)部分穿孔)消聲器做了相應(yīng)的研究[2]。熊馳運用傳遞導(dǎo)納理論模型對直通穿孔管消聲器進行聲學(xué)有限元分析,得到了同尺寸擴張腔消聲器和穿孔管消聲器的傳遞損失曲線對比圖[3]。徐磊等詳細討論過直通穿孔消聲器的設(shè)計參數(shù)對消聲器傳遞損失的相關(guān)影響[4]。縱觀近年來許多學(xué)者在穿孔管結(jié)構(gòu)消聲器方面的研究,可知部分穿孔消聲器的低頻共振峰與穿孔進出口的外插長度有關(guān)[5],但這些研究并未描述低頻共振峰隨外插長度變化的具體關(guān)系,也未說明除外插長度外還與哪些參數(shù)有關(guān),各參數(shù)對共振峰偏移影響的大小有何不同。劉晨利用分析橫流通過消聲器的聲學(xué)衰減特性,表明傳遞損失會隨著氣流速度的增加而向低頻偏移[6]。馬勇利用Machel公式降低穿孔管消聲器模擬的復(fù)雜性,施加阻力邊界條件對消聲器進行模擬[7],發(fā)現(xiàn)橫流穿孔管消聲器消聲特性好于直通穿孔管消聲器。本文主要研究目的在于:
(1)討論部分穿孔結(jié)構(gòu)消聲器的有效消聲頻段與穿孔率變化的關(guān)系、對低頻消聲共振峰偏移的影響規(guī)律。
(2)比較相同穿孔率情況下部分穿孔消聲器左右兩端插入長度不同對低頻共振消聲峰偏移的影響規(guī)律,比較穿孔率和插入長度兩個設(shè)計因素對低頻共振峰偏移影響的大小。
(3)在穿孔數(shù)目、半徑、左右插入穿孔段長度一定的情況下,討論穿孔周向、軸向分布對部分穿孔消聲器消聲性能的影響。
(4)在固定穿孔率、左右插入長度、穿孔段長度一定的情況下討論擴張腔直徑的改變對部分穿孔消聲器有效消聲頻率范圍的影響。
1 理論基礎(chǔ)
1.1 三維聲波方程
聲學(xué)有限元的基礎(chǔ)方程是建立在三維聲波方程之上的,滿足理想介質(zhì)、無粘性無能量損耗、聲傳播過程中無能量交換、介質(zhì)振幅小、聲場各階參數(shù)都是1階微量的條件。

將式(1)代入

得到

其中p為聲壓,p(x,y,z)為空間位置上的聲壓幅值,k為波數(shù),,ω為聲波角頻率,c為聲速。
1.2 有限元法
有限元法的基本思想是將要求解的集合區(qū)域離散、分解成有限個單元,在各個單元之間布置有限個節(jié)點,用這些所有的單元和節(jié)點組成的集合來代替原有的幾何計算區(qū)域。有限元法有著諸如計算精度高、能夠有效地適應(yīng)各種復(fù)雜形狀等優(yōu)點,所以廣泛運用于工程領(lǐng)域的仿真計算。
1.3 傳聲損失的計算
傳聲損失的定義是:消聲器入口聲功率和出口聲功率之比。一般來說消聲器的入口面積與出口面積相等且滿足其他聲學(xué)假設(shè)條件下,傳聲損失的表達式為
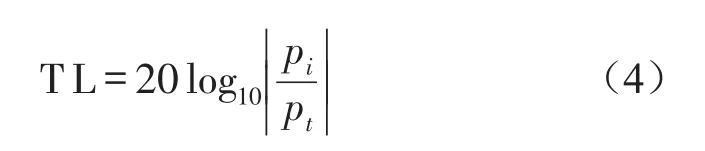
式中pi是消聲器入口入射聲聲壓,pt是消聲器出口投射聲聲壓。
2 仿真的實驗驗證
為了驗證仿真方法對穿孔管消聲器計算的準確性,設(shè)計一個穿孔率為15%的直通穿孔管消聲器,其具體結(jié)構(gòu)參數(shù)為:進出口管徑d=45 mm,擴張腔直徑D=160 mm,擴張腔長度L=370 mm。
圖1為消聲器傳遞損失測試的實驗示意圖,利用LMS Virtual Lab對模型進行仿真計算,對比實驗結(jié)果和仿真結(jié)果見圖2。

圖1 消聲器傳遞損失測試簡圖

圖2 傳遞損失實驗值與仿真值對比
從圖中可以看到,在1 900 Hz以下仿真結(jié)果與實驗值吻合度高,誤差在可接受的范圍,且在15%的大穿孔率情況下穿孔管消聲器的傳遞損失和擴張腔消聲器接近,這也和圖2情況吻合。所以可認為仿真得到的穿孔結(jié)構(gòu)的計算值是可靠的。
3 部分穿孔管消聲器的研究
3.1 穿孔率對低頻共振峰影響
在現(xiàn)實的消聲器設(shè)計中,多數(shù)的時候用的還是部分穿孔管。針對部分穿孔管消聲器設(shè)計如圖3所示的消聲器模型,表1為消聲器具體設(shè)計參數(shù):La= 200 mm,Lb=200 mm,100%穿孔(插入管),得到如下仿真結(jié)果。
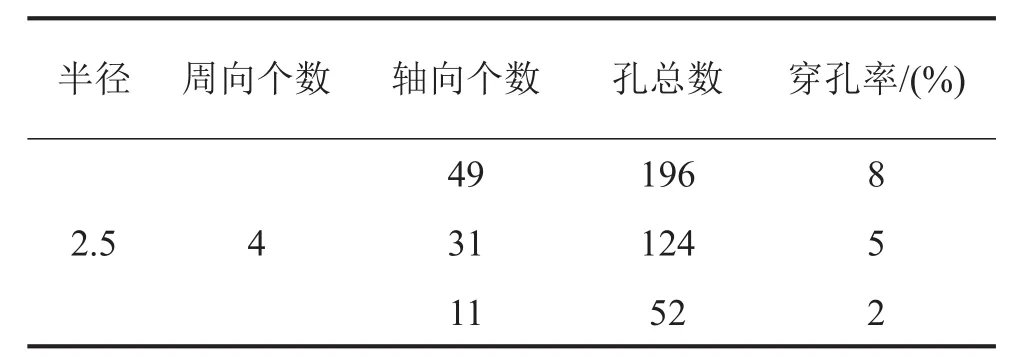
表 1穿孔率不同時的設(shè)計參數(shù)
圖4分別比較了擴張腔消聲器和插入管消聲器傳遞損失之間的差別,由圖可知擴張腔消聲器的傳聲損失曲線在中低頻率部分呈現(xiàn)規(guī)則的拱形。
插入管消聲器的傳聲損失則有所不同,在一些特定的頻率上出現(xiàn)消聲峰值,但其通過頻率幾乎一致。對于插入管消聲器(穿孔率100%),消聲峰出現(xiàn)的原因主要是側(cè)支空腔的存在引起部分聲波在與插入管臨近的腔體中傳播的聲波與主管道傳播的聲波存在相位差導(dǎo)致特定頻率的消聲量增大,這一消聲峰大多也叫作側(cè)支共振峰。可用以下公式表示

圖3 部分穿孔管消聲器與擴張腔消聲器模型
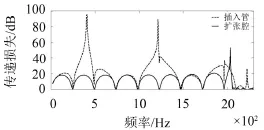
圖4 插入管消聲器與擴張腔消聲器傳遞損失對比
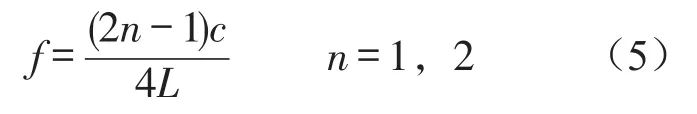
式中f為消聲頻率,c為聲速,L為進出口管的插入長度。
計算出的第1、2階側(cè)支消聲峰值為425 Hz和1 275 Hz,而由仿真計算得到的插入管消聲器的第1、2階消聲峰值分別為415 Hz和1 245 Hz。
由圖5可知部分穿孔管在中低頻時會存在明顯的消聲峰,對比部分穿孔管消聲器和插入管消聲器(100%穿孔)的傳遞損失曲線可以發(fā)現(xiàn),在有效的消聲頻域內(nèi)第2階消聲峰處表現(xiàn)為相鄰的兩個峰,其中有一個消聲峰頻率較低,為穿孔所引起的共振峰,它隨著穿孔率的增大向高頻發(fā)生偏移,另一個則是由插入長度引起的側(cè)支共振峰,這個側(cè)支消聲峰的頻率值與1階側(cè)支消聲峰的頻率值滿足式(5)的三倍關(guān)系,但卻不能用式(5)計算此側(cè)支共振峰。第1階側(cè)支消聲峰隨著穿孔率的增大向高頻偏移,但是偏移量比較小,隨穿孔率的增大,2階峰處的穿孔消聲峰與插入管引起的共振消聲峰越來越靠近,當穿孔率大到極限就成了插入管,此時由穿孔引起的消聲峰與側(cè)支共振引起的2階峰重合。
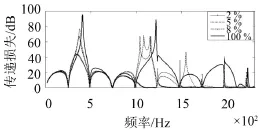
圖5 三種不同穿孔率下的傳遞損失結(jié)果對比
圖5也可以觀察到當穿孔率較小時,消聲器有效消聲頻段也有所變窄,這也使得在小穿孔率的時候在消聲頻譜圖上沒有2階峰顯現(xiàn)。從圖5還可以看出在部分穿孔的情況下,隨著穿孔率的增大,有效消聲頻率范圍也有所拓寬,穿孔率為2%時在1 100 Hz左右就截止,而穿孔率為8%時則在1 710 Hz左右截止。
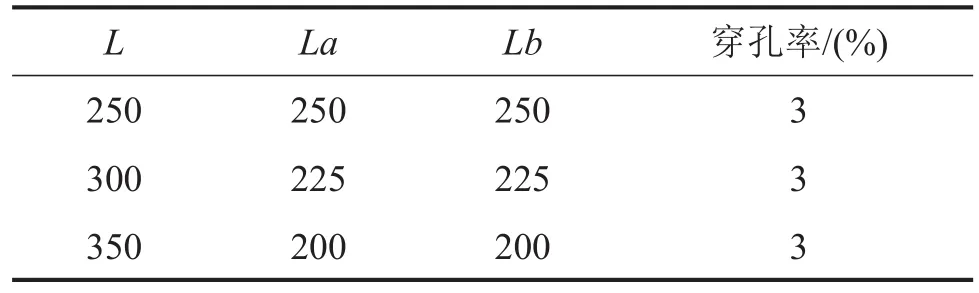
表2 插入長度變化
3.2 不同插入長度變化時低頻消聲峰的變化
為了排除不同插入長度對消聲共振峰的影響,模型設(shè)計時穿孔段都居于消聲器的中間位置,且穿孔率大小都為3%。仿真結(jié)果見圖6,可以看出當La、Lb長度發(fā)生變化即部分穿孔消聲器的插入長度發(fā)生變化,由插入引起的側(cè)支消聲峰會發(fā)生偏移,當La、Lb越小消聲峰越是向高頻偏移。
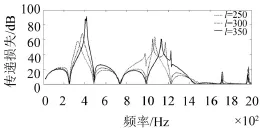
圖6 不同插入長度下傳遞損失結(jié)果對比
對于穿孔所引起的消聲峰,雖然穿孔率沒有發(fā)生變化,但是由于插入長度的不同會改變整個消聲器穿孔段的長度,這也導(dǎo)致整個消聲器的穿孔面積增大,從而導(dǎo)致穿孔引起的消聲峰向高頻發(fā)生偏移。
3.3 穿孔軸向、周向分布對低頻消聲峰的影響
實際的消聲器設(shè)計多采用軸向、周向均勻分布的方式。但是有時由于結(jié)構(gòu)等因素的限制,消聲器難以均勻打孔,也會采取不均勻的方式。上述3個消聲器穿孔半徑、面積、數(shù)目都完全一樣,穿孔段長度l=300位于消聲器擴張腔的中間,只改變其軸向、周向的孔數(shù)分布,由圖7可知3個消聲器的傳聲損失曲線幾乎完全一致,這說明消聲器的設(shè)計中當穿孔數(shù)目、半徑、面積一定時,單純改變部分穿孔消聲器軸向、周向穿孔分布數(shù)目,對消聲器的傳遞損失沒有太大的影響。
3.4 部分穿孔消聲器擴張腔直徑對傳聲損失的影響
圖8為部分穿孔消聲器其他條件都一定的情況下,僅僅改變擴張腔直徑,分別計算擴張腔直徑為150 mm、200 mm、300 mm時得到的傳聲損失曲線。在低頻部分傳聲損失曲線通過頻率、走向幾乎一致,但是隨著擴張腔直徑的增大,拱形消聲曲線的消聲量也會隨之增大。擴張腔增大后還會引起穿孔造成的共振峰與插入造成的共振峰之間的間距增大,這是由于擴張腔直徑增大后會造成共振體積增大,穿孔消聲峰向低頻偏移。

表3 周向、軸向分布
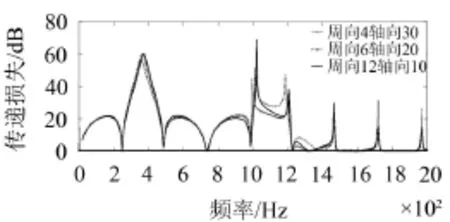
圖7 穿孔總數(shù)相同而周向、軸向分布不同時傳遞損失的比較

圖8 不同擴張腔直徑對傳遞損失的影響
除穿孔率會對消聲頻率范圍產(chǎn)生影響外,擴張腔直徑也會對此產(chǎn)生影響,從上面的消聲曲線頻譜圖可以看到d=300 mm時有效消聲截止頻率大約為1 300 Hz,d=150 mm時有效消聲截止頻率約為1 700 Hz。產(chǎn)生這個現(xiàn)象的原因是由于聲波透過穿孔在擴張腔內(nèi)按平面波形式傳播,而圓形截面聲波導(dǎo)管的平面波截止頻率又與聲波導(dǎo)管直徑有關(guān),直徑越大聲波的截止頻率也越低,這與上圖仿真結(jié)果是一致的,由此可以看出部分穿孔消聲器的有效消聲頻率范圍與穿孔率和擴張腔直徑都有關(guān)系。
4 結(jié)語
(1)對于部分穿孔消聲器,穿孔率的增大會引起低頻側(cè)支共振消聲峰向高頻偏移,但是偏移不是很劇烈,消聲性能曲線的有效頻率隨著穿孔率的增大而拓寬。根據(jù)消聲峰的偏移規(guī)律估計部分穿孔管消聲峰出現(xiàn)的位置,這在實際的設(shè)計中十分有意義。
(2)當部分穿孔管消聲器插入長度變長,側(cè)支共振消聲峰向低頻偏移,穿孔共振消聲峰的偏移與實際的穿孔面積有關(guān),與穿孔率關(guān)系不大。
(3)穿孔半徑、總數(shù)一定時,無論軸向、周向穿孔的分布如何,都不會對消聲器的消聲性能產(chǎn)生影響。
(4)在其他設(shè)計參數(shù)都一致的情況下,隨著部分穿孔消聲器擴張比腔直徑的增大,消聲器低頻拱形消聲量有所增大,且消聲性能曲線的有效消聲頻率范圍也有所拓寬。
[1]SELAMET A,XU M B,LEE I J.Analytical approach for sound attenuation in perforated dissipative silencers[J].Journal of Acoustical Society of America,2004,115(5): 2091-2099.
[2]季振林.直通穿孔管消聲器聲學(xué)性能計算及分析[J].哈爾濱工程大學(xué)學(xué)報,2005;26(3):302-306.
[3]熊馳,陳永光,蔡偉明.穿孔管式消聲單元消聲性能仿真分析[J].公路與汽運,2014,160(1):15-17.
[4]徐磊,劉正士,畢嶸.結(jié)構(gòu)參數(shù)對直通穿孔管消聲器消聲性能影響的數(shù)值分析[J].合肥工業(yè)大學(xué)學(xué)報,2009;32(11):1637-1641.
[5]黎志勤,黎蘇.汽車排氣系統(tǒng)噪聲與設(shè)計[M].北京:中國環(huán)境科學(xué)出版社,1991.
[6]劉晨,季振林,徐航手.穿孔管消聲器聲學(xué)性能三維時域計算及分析[J].機械工程學(xué)報,2012;48(10):7-13.
[7]馬勇,鐘成,張洪濤.直通穿孔管消聲器與橫流穿孔管消聲器消聲性能對比研究[J].農(nóng)業(yè)裝備與車輛工程,2012,246(1):40-45.
Finite ElementAnalysis ofAcousticAttenuation Performance of Partially Perforated Tube Silencers
WEN Yi-yun,DENG Zhao-xiang,ZHANG Yang
(College of Mechanical Engineering,Chongqing University,Chongqing 400044,China)
Since the perforated pipe silencer has a good acoustic attenuation performance and a low pressure loss,it is used to eliminate the noise of the engine exhaust systems.In this paper,influences of the perforation rate,insertion length, circumferential and axial perforation distributions,inflation lumen diameter etc.on the acoustic attenuation performance of the muffler are studied by means of the finite element method.It is concluded that increasing of the perforation rate and decreasing of the insertion length can cause the low-frequency resonance peak to shift to the high frequency direction; increasing of the perforation rate and decreasing of the inflation lumen diameter can widen the frequency range of the effective noise elimination.While the axial and circumferential distributions of perforation have little influence on acoustic attenuation performance of the muffler.
acoustics;transmission loss;acoustic attenuation performance;partially perforated muffler;finite element method;structural parameters
TK413.4+7
:A
:10.3969/j.issn.1006-1335.2016.06.036
1006-1355(2016)06-0182-04
2016-06-22
溫逸云(1991-),男,重慶市墊江縣人,碩士生,主要研究方向為內(nèi)燃機排氣系統(tǒng)。Email:wenyiyunlinxiou@163.com
鄧兆祥,男,教授,博士生導(dǎo)師。E-mail:zxdeng@cqu.edu.cn

