艙筏系統(tǒng)中隔振器多向阻抗的辨識(shí)

孫 巍，徐時(shí)吟

（1.海軍駐滬東中華造船集團(tuán)有限公司軍事代表室 上海 200129；2.上海交通大學(xué) 機(jī)械系統(tǒng)與振動(dòng)國家重點(diǎn)實(shí)驗(yàn)室，上海 200240）

艙筏系統(tǒng)中隔振器多向阻抗的辨識(shí)

孫 巍1，徐時(shí)吟2

（1.海軍駐滬東中華造船集團(tuán)有限公司軍事代表室 上海 200129；2.上海交通大學(xué) 機(jī)械系統(tǒng)與振動(dòng)國家重點(diǎn)實(shí)驗(yàn)室，上海 200240）

針對艙筏系統(tǒng)中的橡膠隔振器，構(gòu)建由剛體質(zhì)量塊以及待測隔振器所組成的耦合系統(tǒng)模型。利用試驗(yàn)測得的系統(tǒng)整體及剛體質(zhì)量塊的導(dǎo)納矩陣，采用子結(jié)構(gòu)分解方法得到隔振器的多向阻抗矩陣。辨識(shí)結(jié)果與測試結(jié)果吻合較好，驗(yàn)證子結(jié)構(gòu)分解法對隔振器多向阻抗辨識(shí)的有效性，為艙筏系統(tǒng)的精細(xì)化建模提供參考。

振動(dòng)與波；艙筏系統(tǒng)；隔振器；子結(jié)構(gòu)分解法；多向阻抗

潛艇聲隱身性能是保證其能在復(fù)雜多變的戰(zhàn)場上生存的首要因素。潛艇的輻射噪聲有三大來源，分別為機(jī)械噪聲、螺旋槳噪聲和水動(dòng)力噪聲[1]。之前的研究指出[2,3]，機(jī)械噪聲是潛艇在低速巡航工況下最為主要的噪聲來源，其在潛艇的總輻射噪聲中所占的比重能夠達(dá)到七成左右。潛艇機(jī)械噪聲的控制可以從聲源和傳遞途徑這兩個(gè)方面來著手實(shí)施，隔振是工程實(shí)際中最為常用也是最行之有效的手段。通過在振源和基座之間附加一個(gè)子系統(tǒng)，改變振源對系統(tǒng)激勵(lì)的能量頻譜結(jié)構(gòu)以達(dá)到振動(dòng)抑制的目的。現(xiàn)代潛艇中的機(jī)械設(shè)備普遍進(jìn)行隔振處理，尤其是艙筏隔振技術(shù)的應(yīng)用大幅提升了潛艇的聲隱身性能[4]。

艙筏隔振系統(tǒng)是一種受復(fù)雜振源作用的多彈性支撐隔振系統(tǒng)，多點(diǎn)多向耦合效應(yīng)對于系統(tǒng)振動(dòng)傳遞有很大的影響。Sanderson研究了多支撐系統(tǒng)在考慮多向振動(dòng)傳遞時(shí)，外力和彎矩激勵(lì)下的運(yùn)動(dòng)傳遞和能量傳遞[5]。研究結(jié)果表明，在計(jì)算中忽略系統(tǒng)的轉(zhuǎn)角自由度會(huì)使對功率流傳遞的預(yù)測出現(xiàn)偏差，偏差程度取決于隔振器的阻抗和基礎(chǔ)連接點(diǎn)處輸入導(dǎo)納之間的比值。為了能在模型中體現(xiàn)出多向自由度耦合的影響，建模時(shí)需要用到隔振器多向阻抗矩陣及系統(tǒng)子結(jié)構(gòu)多向頻響矩陣，而這兩項(xiàng)數(shù)據(jù)的精確獲取也是建模過程中的難點(diǎn)。

隔振器作為彈性元件是艙筏隔振系統(tǒng)中的關(guān)鍵組成部分，準(zhǔn)確描述隔振器動(dòng)力學(xué)特性是研究系統(tǒng)振動(dòng)傳遞的前提條件。文獻(xiàn)[6]中指出，當(dāng)激勵(lì)不是施加在質(zhì)心位置時(shí)，會(huì)引起機(jī)組的搖擺振動(dòng)。受此影響，隔振器將會(huì)出現(xiàn)彎曲變形，僅靠垂向阻抗或者3個(gè)平動(dòng)方向的阻抗無法對隔振器的動(dòng)力學(xué)特性做出準(zhǔn)確的描述。如果在建模過程中僅考慮隔振器的平動(dòng)阻抗，忽略彎曲阻抗的影響，會(huì)導(dǎo)致計(jì)算得到的系統(tǒng)響應(yīng)結(jié)果出現(xiàn)誤差，給艙筏系統(tǒng)的精細(xì)化建模帶來不利影響。

對于隔振器阻抗矩陣的獲取，已經(jīng)開展了大量的研究工作，包括集總參數(shù)模型[7]和連續(xù)體模型[8]。但是上述兩種模型都很難準(zhǔn)確描述實(shí)際隔振器的動(dòng)力學(xué)特性。因此針對具體型號的隔振器，通過試驗(yàn)測量得到其阻抗是更合理的做法。試驗(yàn)方法可以分為直接法和間接法，前者常用于隔振器三向平動(dòng)阻抗的測量，具體詳見文獻(xiàn)[9]。而間接試驗(yàn)方法通過測試包含待測隔振器及已知參數(shù)質(zhì)量塊的振動(dòng)系統(tǒng)，利用系統(tǒng)以及質(zhì)量塊的輸入輸出特性求解隔振器的導(dǎo)納，進(jìn)而求逆得到其阻抗矩陣[10]。文中針對艙筏隔振系統(tǒng)中的BE型橡膠隔振器，通過間接方法，對艙筏系統(tǒng)中所采用的橡膠隔振器的多向阻抗特性進(jìn)行辨識(shí)，基于子結(jié)構(gòu)分解從試驗(yàn)數(shù)據(jù)中獲取隔振器的多向阻抗信息，為構(gòu)建基于試驗(yàn)的艙筏系統(tǒng)精細(xì)化模型提供參考。

1 子結(jié)構(gòu)導(dǎo)納分解法

建立如圖1中所示的耦合系統(tǒng)模型，其由三個(gè)子結(jié)構(gòu)組成，將子結(jié)構(gòu)P作為子結(jié)構(gòu)S和R之間的彈性連接件。在已知系統(tǒng)整體導(dǎo)納以及子結(jié)構(gòu)S、R導(dǎo)納的前提下，通過分解方法得到彈性連接件P的導(dǎo)納矩陣。

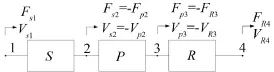
圖1 由振源-傳遞路徑-受體組成的耦合系統(tǒng)

圖中系統(tǒng)各節(jié)點(diǎn)的編號為1-4，VSi、VPi和VRi是各節(jié)點(diǎn)處的響應(yīng)，F(xiàn)Si是作用于子結(jié)構(gòu)S上的激勵(lì)力向量，F(xiàn)Pi和FRi是連接點(diǎn)處的傳遞力向量。響應(yīng)與力之間的關(guān)系可以表示為

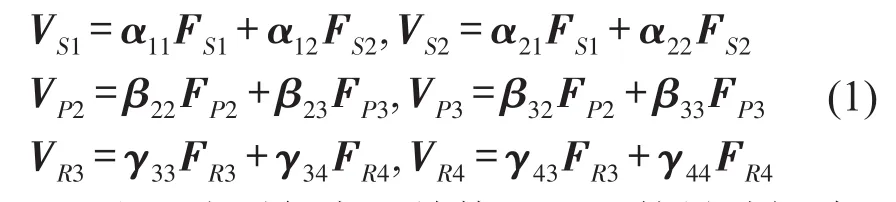
式中αij、βij和γij分別代表子結(jié)構(gòu)S、P、R的導(dǎo)納矩陣。連接點(diǎn)處的力平衡條件和位移協(xié)調(diào)條件為

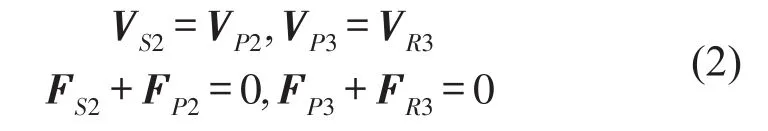
將式(1)代入式(2)，并利用式(2)中的等式關(guān)系，可以得到節(jié)點(diǎn)2處的傳遞力

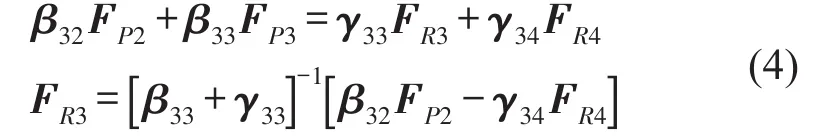
將式(3)代入式(4)，并利用式(2)中所給出的關(guān)系式，可以得到在點(diǎn)1和點(diǎn)4處施加激勵(lì)時(shí)點(diǎn)3處受到的傳遞力

通過同樣方法可以得到節(jié)點(diǎn)3處的傳遞力

通過同樣方法可以得到子結(jié)構(gòu)1、2之間的傳遞力

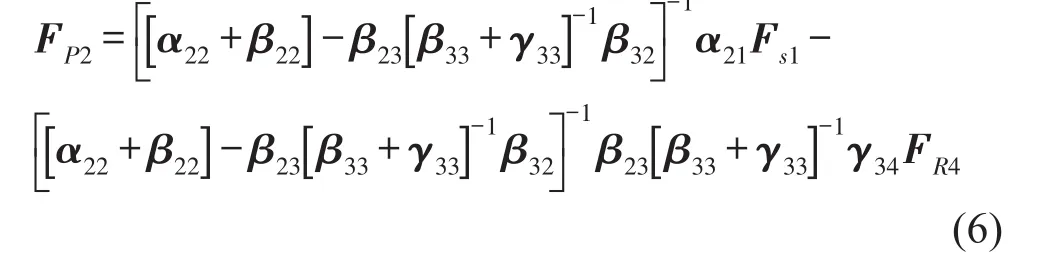
當(dāng)只有節(jié)點(diǎn)1受到外力作用時(shí)，式(5)和式(6)可以分別簡化為同樣，當(dāng)只有節(jié)點(diǎn)4受到外力作用時(shí)，式(5)和式

(6)可以簡化為

對于圖1中所示的系統(tǒng)，令其導(dǎo)納為Mij，可以得到V1=M11FS1，V1=M14FR4，V4=M41FS1，V4=M44FR4。用子結(jié)構(gòu)的導(dǎo)納αij、βij和γij來表示Mij，以M11為例說明推導(dǎo)的過程。聯(lián)立式(8)和式(2)得到FS2，將其代入式(1)得到節(jié)點(diǎn)1處受單位激勵(lì)時(shí)原點(diǎn)處的響應(yīng)

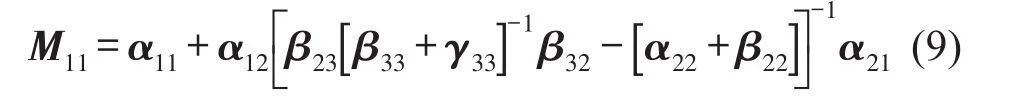
同理，可以得到系統(tǒng)其余導(dǎo)納矩陣M41、M14、M44。

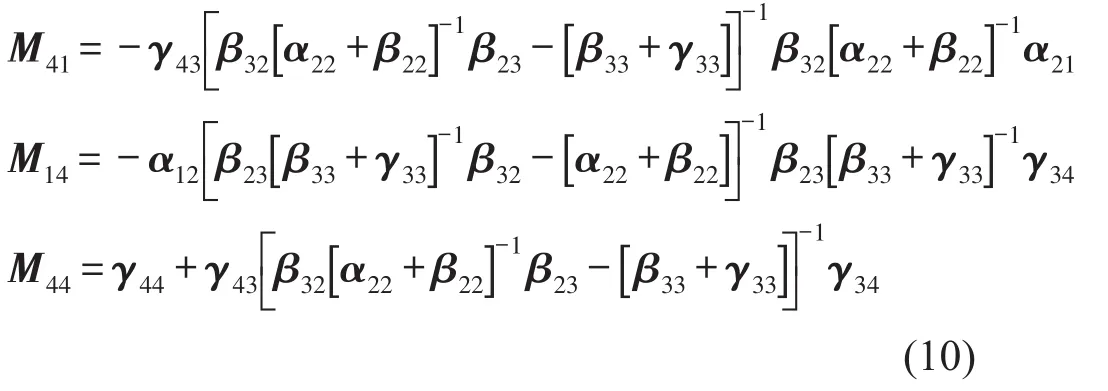
基于求得的耦合系統(tǒng)導(dǎo)納矩陣，可以進(jìn)一步推得彈性連接件的導(dǎo)納βij關(guān)于Mij及αij、γij的函數(shù)表達(dá)式。將式(9)和式(10)的第二項(xiàng)分別改寫為

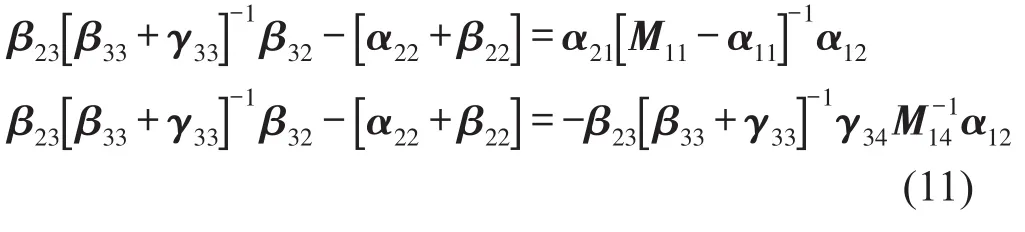
通過式(11)可以得到

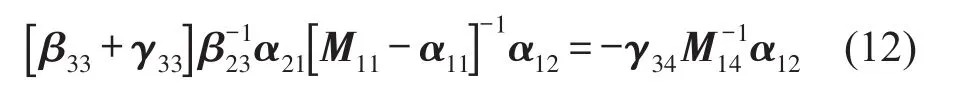
同理將式(10)的第一項(xiàng)和第三項(xiàng)改寫為

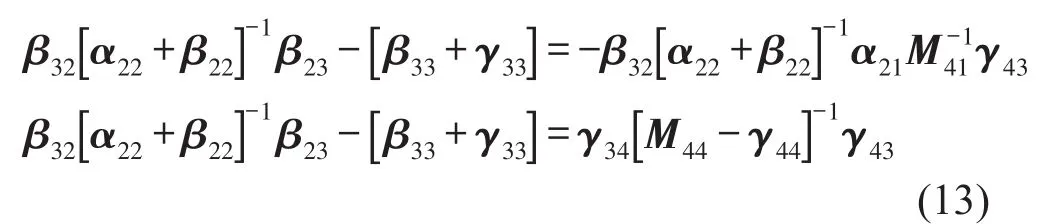
對式(10)的第二、第三項(xiàng)求解關(guān)于[β33+γ33]的方程可以得到

對式(14)進(jìn)行簡化

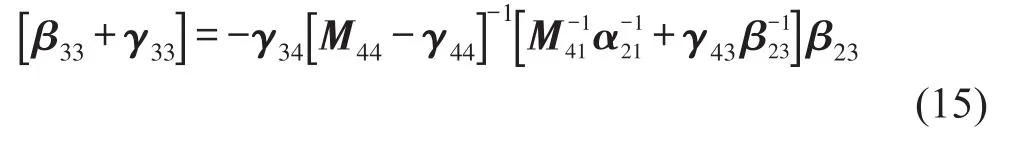
再將式(15)代入式(12)，可以得到

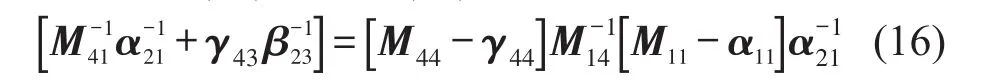
由式(16)可以得到彈性連接件的傳遞導(dǎo)納β23

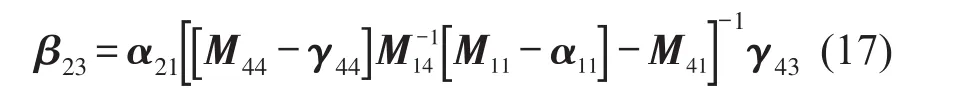
再將式(17)代入式(12)可以得到彈性連接件的原點(diǎn)導(dǎo)納

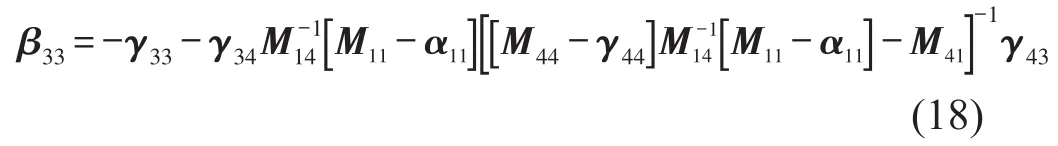
通過同樣方法可以得到β22和β32，對式(13)求解關(guān)于[α22+β22]的方程同時(shí)對式(11)求解關(guān)于[α22+β22]的方程，可以得到

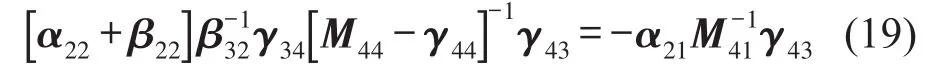
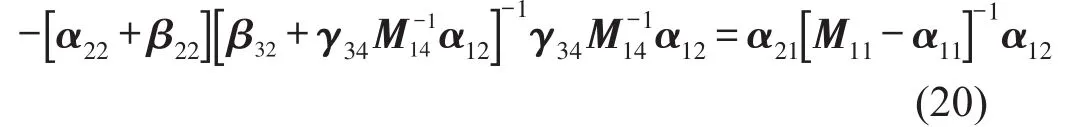
式(20)可以簡化為

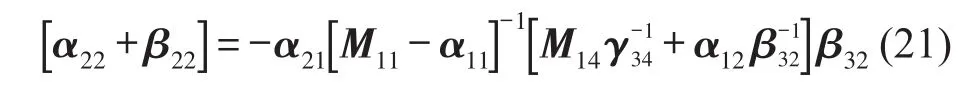
將式(21)代人式(19)可以得到

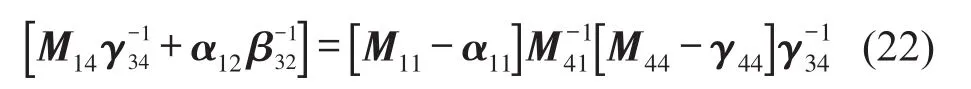
由式(22)可以得到彈性連接件的傳遞導(dǎo)納β32

將式(23)代入式(19)可以得到其原點(diǎn)導(dǎo)納β22

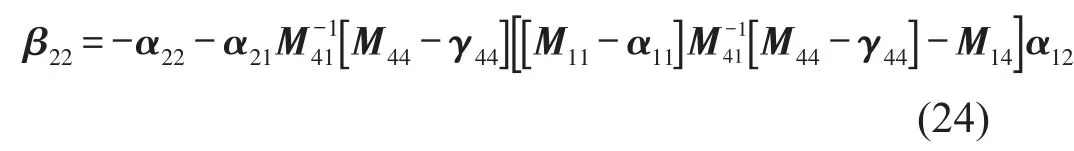
進(jìn)一步將原點(diǎn)導(dǎo)納簡化為

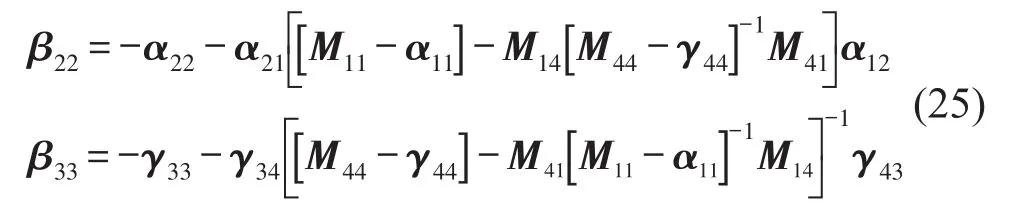
2 基于子結(jié)構(gòu)分解的橡膠隔振器多向阻抗的獲取

2.1 實(shí)驗(yàn)?zāi)Ｐ?/p>

通過實(shí)驗(yàn)測試獲取艙筏系統(tǒng)中所采用的橡膠隔振器的多向阻抗矩陣。基于子結(jié)構(gòu)分解方法，以隔振器為待測子結(jié)構(gòu)建立對應(yīng)的耦合系統(tǒng)模型。圖2給出了橡膠隔振器的示意圖和實(shí)物照片，具體采用的隔振器型號為BE-15和BE-60型隔振器，尺寸參數(shù)如表1所示。

圖2 BE型橡膠隔振器

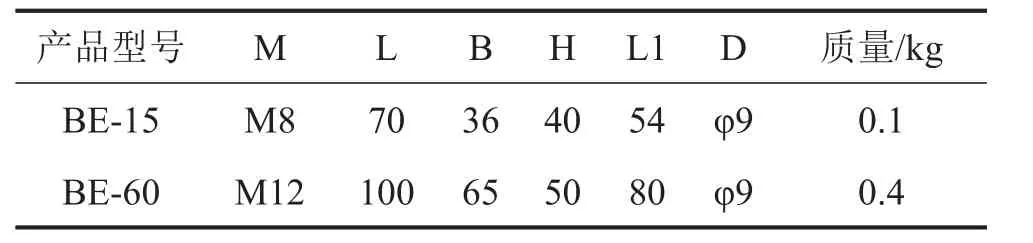
表1 隔振器的結(jié)構(gòu)尺寸/mm及其質(zhì)量/kg

試驗(yàn)系統(tǒng)由質(zhì)量塊和待測隔振器組成，圖3為試驗(yàn)系統(tǒng)示意圖，圖中垂直于紙面的方向?yàn)閦軸。如圖所示，點(diǎn)1和點(diǎn)4分別為質(zhì)量塊1和質(zhì)量塊2上的參考點(diǎn)，而點(diǎn)2和點(diǎn)3分別為質(zhì)量塊與待測隔振器之間的連接點(diǎn)。類比于圖1中所示的耦合系統(tǒng)，令待測隔振器的導(dǎo)納為βij(i，j=2，3)，隔振器左右兩端質(zhì)量塊的導(dǎo)納分別為αij(i，j=1，2)和γij(i，j=3，4)，而耦合系統(tǒng)的整體導(dǎo)納矩陣為Mij(i，j=1，4)。

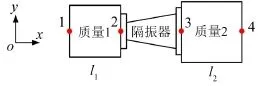
圖3 試驗(yàn)?zāi)Ｐ褪疽鈭D

圖4為試驗(yàn)裝置，待測隔振器兩端分別通過螺栓與剛性質(zhì)量塊相連。對應(yīng)于BE-15型隔振器的剛性質(zhì)量塊尺寸分別為0.06 m×0.08 m×0.1 m和0.06 m×0.1 m×0.1 m，而對應(yīng)于BE-60型隔振器的剛性質(zhì)量塊尺寸分別為0.085 m×0.1 m×0.14 m和0.085 m×0.14 m×0.14 m。

圖4 耦合系統(tǒng)試驗(yàn)?zāi)Ｐ?/p>

假設(shè)系統(tǒng)在各個(gè)平面內(nèi)的運(yùn)動(dòng)是相互獨(dú)立的，因此需要依次對隔振器在每個(gè)平面內(nèi)的導(dǎo)納矩陣進(jìn)行辨識(shí)。下面將以xoy平面作為例子，對分解方法進(jìn)行具體說明。

2.2 質(zhì)量塊的導(dǎo)納矩陣

通過剛體理論可以得到質(zhì)量塊上任意兩點(diǎn)之間導(dǎo)納的解析表達(dá)式，從而建立質(zhì)量塊在xoy平面內(nèi)的導(dǎo)納矩陣

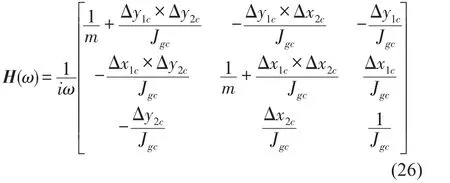
式中m表示質(zhì)量塊的質(zhì)量，xi、yi表示激勵(lì)點(diǎn)和響應(yīng)點(diǎn)的坐標(biāo)，xc、yc表示質(zhì)量塊的質(zhì)心坐標(biāo)，而質(zhì)量塊激勵(lì)點(diǎn)、響應(yīng)點(diǎn)與質(zhì)心之間的相對位置可以分別表示為

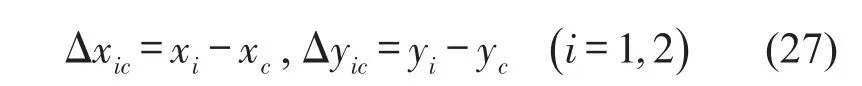
2.3 耦合系統(tǒng)的導(dǎo)納矩陣

耦合系統(tǒng)的導(dǎo)納矩陣直接由試驗(yàn)測得，式(28)為其導(dǎo)納矩陣。這里將以點(diǎn)1處的原點(diǎn)導(dǎo)納M11為例，說明系統(tǒng)導(dǎo)納的測試流程。面內(nèi)運(yùn)動(dòng)擁有三向自由度(ux，uy，θz)，因此M11是一個(gè)3×3的矩陣。其中沿x軸的縱向運(yùn)動(dòng)獨(dú)立于其余兩向自由度，而沿y軸的橫向運(yùn)動(dòng)和繞z軸的彎曲運(yùn)動(dòng)之間存在相互耦合關(guān)系。為了得到完整的原點(diǎn)導(dǎo)納矩陣，需要在三個(gè)方向分別施加激勵(lì)。在試驗(yàn)中針對每向激勵(lì)設(shè)計(jì)了對應(yīng)的測試工況，圖5給出了具體的測試流程圖及測點(diǎn)位置。

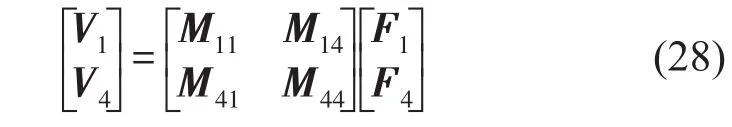
工況1測試系統(tǒng)沿x向的導(dǎo)納，在點(diǎn)1處施加縱向力fx1,1，同時(shí)在點(diǎn)1布置沿x向的傳感器，測得點(diǎn)1的縱向加速度響應(yīng)vx1,1，下標(biāo)中第一項(xiàng)x1代表點(diǎn)1處x方向的力或位移，下標(biāo)中的第2項(xiàng)代表測試工況的編號。工況2中點(diǎn)1處受到橫向力fy1,2，在點(diǎn)1和點(diǎn)2位置沿y向布置傳感器。由于沿y向及繞z軸的運(yùn)動(dòng)是相互耦合的，橫向力fy1,2會(huì)激發(fā)隔振器的彎曲變形，需要同時(shí)測量橫向位移和繞z軸的轉(zhuǎn)角。受試驗(yàn)條件的限制，無法直接測得點(diǎn)1位置的轉(zhuǎn)角，通過對相鄰的1、2號測點(diǎn)的垂向響應(yīng)vy1,2、vy2,2進(jìn)行差分，近似計(jì)算點(diǎn)1處的轉(zhuǎn)角θz1,2。工況3測試系統(tǒng)在彎矩作用下的響應(yīng)，由于無法直接在結(jié)構(gòu)上施加彎矩，同樣采用近似的方法，在點(diǎn)2處施加橫向激勵(lì)fy2,3，將其等效為作用在1號點(diǎn)的繞z軸彎矩以及作用在2號點(diǎn)的橫向力，在點(diǎn)1和點(diǎn)2位置沿y向布置傳感器，測得系統(tǒng)在該激勵(lì)下的橫向位移vy1,3和近似轉(zhuǎn)角θz1,3。

將三種工況下的測試結(jié)果整理成矩陣形式

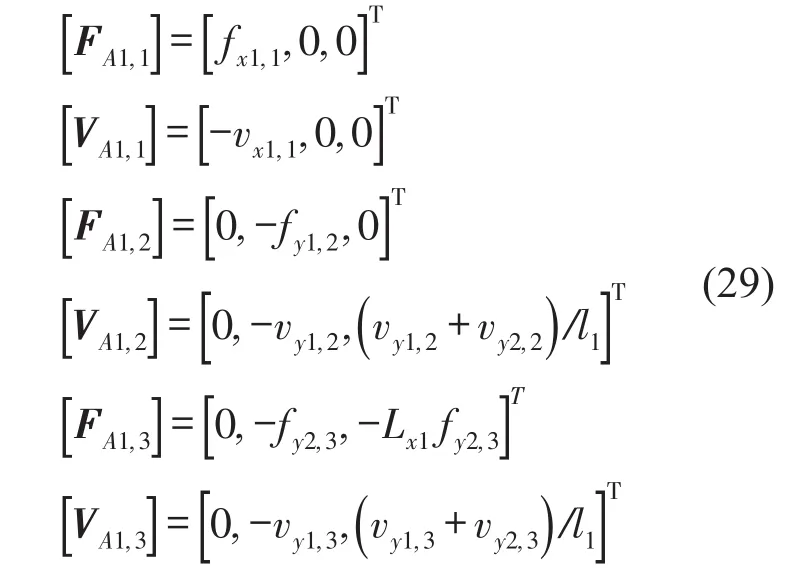
而系統(tǒng)的原點(diǎn)導(dǎo)納M11可以表示為

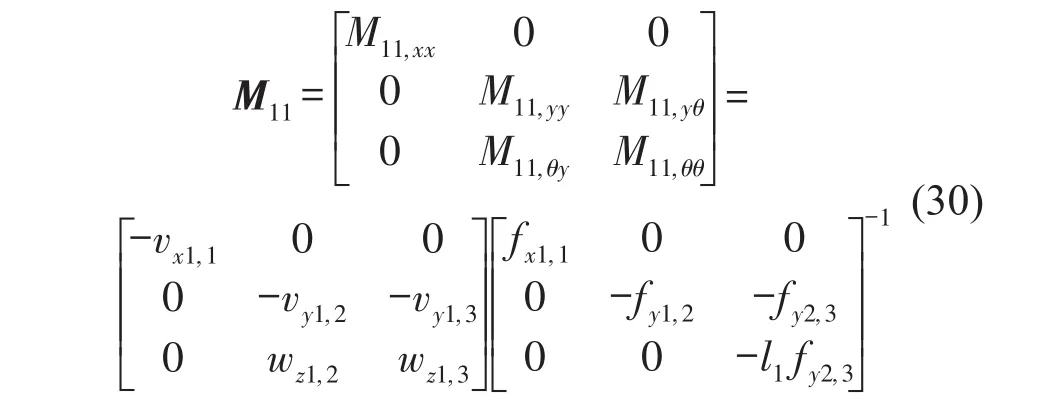
通過同樣的流程，可以分別得到參考點(diǎn)1-4、4-1、4-4之間的導(dǎo)納矩陣M14、M41和M44

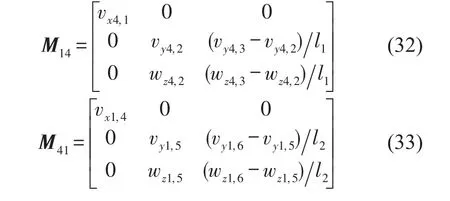
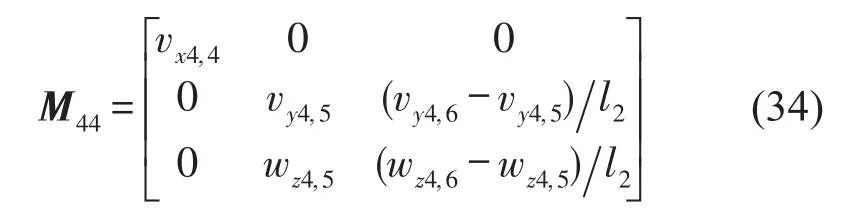
試驗(yàn)測試系統(tǒng)包括三個(gè)部分：激勵(lì)源、數(shù)據(jù)采集系統(tǒng)和數(shù)據(jù)處理系統(tǒng)。激勵(lì)源主要由信號發(fā)生器、功率放大器和激振器等組成；數(shù)據(jù)采集系統(tǒng)和數(shù)據(jù)處理系統(tǒng)主要由電荷放大器、力傳感器、加速度傳感器以及LMS數(shù)據(jù)采集和動(dòng)態(tài)信號分析儀組成。在試驗(yàn)中，將試驗(yàn)對象自由懸掛，令其在水平方向處于自由狀態(tài)，精確調(diào)節(jié)懸掛繩的長度，盡量使質(zhì)量塊及隔振器的中心處于同一水平面。圖5中給出了不同工況下的激勵(lì)情況和測點(diǎn)分布，測量時(shí)將加速度傳感器通過小螺桿固定在結(jié)構(gòu)上，采集測點(diǎn)處的振動(dòng)加速度信號，將電磁激振器平放在U型支架上，沿水平方向施加激勵(lì)。采用的信號為寬帶白噪聲信號，頻率帶寬取為1 024 Hz，頻率分辨率為0.5 Hz。

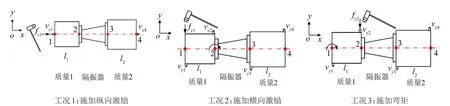
圖 5耦合系統(tǒng)導(dǎo)納M11測試流程圖

2.4 隔振器導(dǎo)納矩陣的辨識(shí)

根據(jù)已知的耦合系統(tǒng)以及質(zhì)量塊的導(dǎo)納矩陣，結(jié)合第1節(jié)中介紹的分解方法，由式(17)、式(23)和式(25)得到隔振器在xoy平面內(nèi)的各向?qū)Ъ{β22、β23、β32、β33。通過對導(dǎo)納矩陣進(jìn)行求逆運(yùn)算，即可得到隔振器的各向阻抗數(shù)據(jù)，而隔振器其余自由度方向的阻抗矩陣可以通過相同的流程獲得。圖6中給出了通過子結(jié)構(gòu)分解方法得到的BE-60型隔振器在xoy平面內(nèi)的各向阻抗，在圖6(a)中將阻抗平臺(tái)測試得到的隔振器縱向阻抗與分解結(jié)果進(jìn)行了對比。如圖所示，隔振器輸入輸出端之間的跨點(diǎn)導(dǎo)納吻合情況良好，而隔振器的原點(diǎn)阻抗在波谷處存在一定的誤差，辨識(shí)結(jié)果和測試結(jié)果不能很好的吻合。誤差可能是由于測試中采用了不同的邊界條件所導(dǎo)致的，在阻抗臺(tái)測試中需要將隔振器一端固定在臺(tái)架上，而在本試驗(yàn)中采用的是自由邊界。

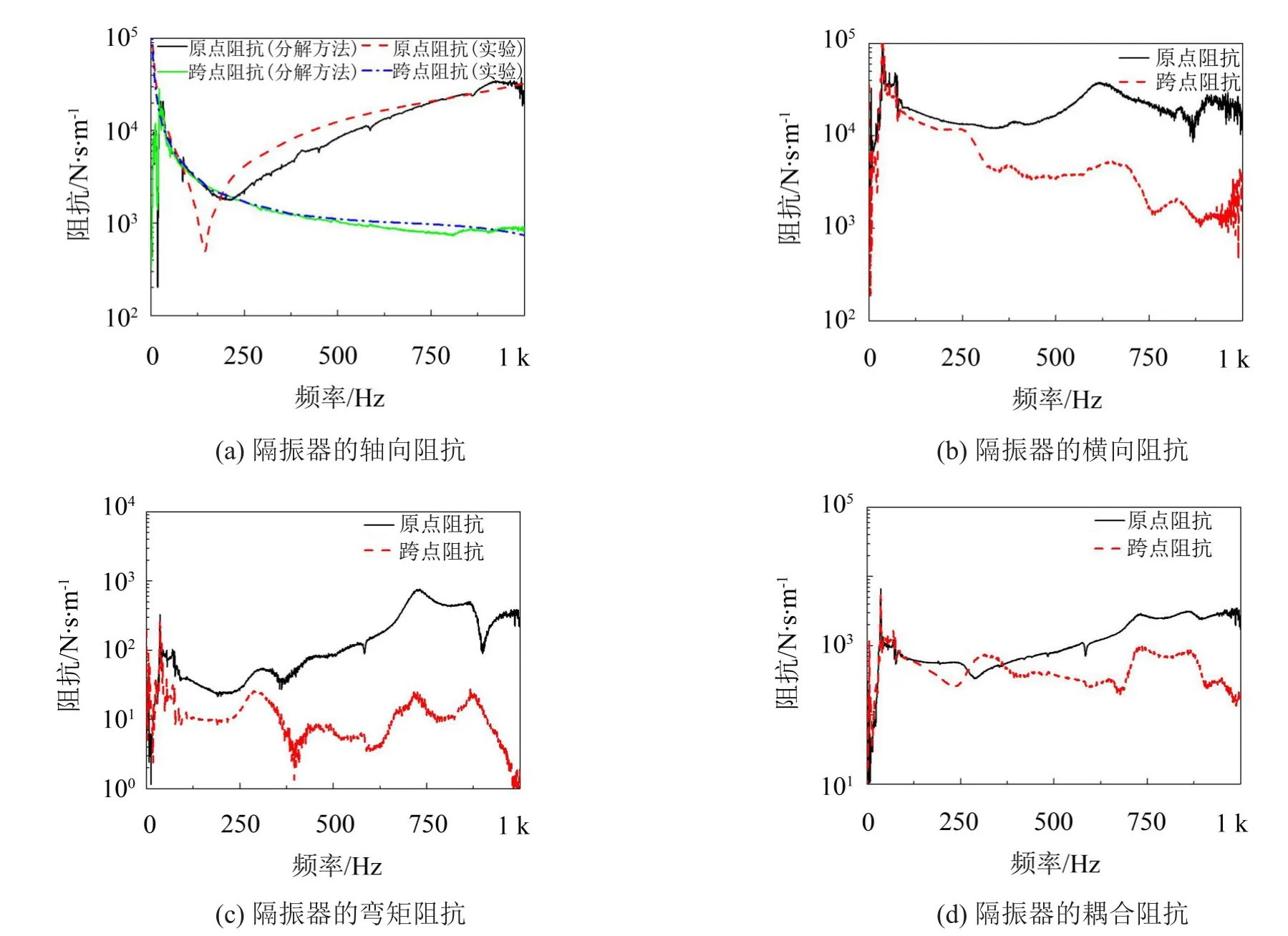
圖6 辨識(shí)得到的隔振器阻抗

3 結(jié)語

針對艙筏系統(tǒng)中的BE型橡膠隔振器，構(gòu)建了由剛體質(zhì)量塊以及待測隔振器所組成的耦合系統(tǒng)模型。采用子結(jié)構(gòu)分解方法得到隔振器的多向阻抗矩陣。分解方法得到的結(jié)果與實(shí)驗(yàn)結(jié)果吻合較好，驗(yàn)證了子結(jié)構(gòu)分解法的有效性，研究結(jié)論為構(gòu)建基于試驗(yàn)的艙筏系統(tǒng)精細(xì)化模型提供參考。

[1]陳志堅(jiān)，夏齊強(qiáng)，艾海峰.潛艇典型結(jié)構(gòu)的聲振特性研究概況及聲學(xué)設(shè)計(jì)構(gòu)想[J].噪聲與振動(dòng)控制，2012，32(2)：1-6.

[2]姚耀中，林立.潛艇機(jī)械噪聲控制技術(shù)綜述[J].艦船科學(xué)技術(shù)，2007，29(1)：21-26.

[3]姚耀中，林立.潛艇機(jī)械噪聲控制技術(shù)的現(xiàn)狀與發(fā)展[J].艦船科學(xué)技術(shù)，2006，28(2)：3-8.

[4]程世祥，張志誼，華宏星.周期桁架結(jié)構(gòu)浮筏隔振特性分析與實(shí)驗(yàn)研究[J].噪聲與振動(dòng)控制，2011，31(6)：5-9.

[5]SANDERSON M.Vibration isolation:Moments and rotations included[J].Journal of Sound and Vibration, 1996,198(2):171-191.

[6]黃修長.艙筏隔振系統(tǒng)聲學(xué)設(shè)計(jì)及優(yōu)化、控制[D].上海：上海交通大學(xué)，2011.

[7]XIUCHANG H,SHIYIN X,AIHUA J,et al.Modeling and optimization of floating raft systems in submarines underdifferentobjectives by using hybrid genetic algorithm[J].Journal of Vibration and Control,2012, 18(2):268-297.

[8]KARI L.On the waveguide modelling of dynamic stiffness of cylindrical vibration isolators.Part i:The model,solution and experimental comparison[J].Journal of Sound and Vibration,2001,244(2):211-233.

[9]DICKENS J,NORWOOD C.Universal method to measure dynamic performance of vibration isolators under static load[J].Journal of Sound and Vibration,2001, 244(4):685-696.

[10]KIM S,SINGH R.Multi-dimensional characterization of vibration isolators over a wide range of frequencies[J].Journal of Sound and Vibration,2001,245(5):877-913.

Multi-directional Impedance Identification of the Rubber Isolator in Floating Raft Systems

SUN Wei1,XU Shi-yin2
(1.Naval Military Representative Office in Hudong Zhonghua Shipyard(Group)Co.Ltd., Shanghai 200129,China; 2.State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University, Shanghai 200240,China)

The coupled system model composed by rigid mass block and the un-calibrated isolator is constructed for the rubber isolator in the floating raft system.Based on the experimental data of the admittance matrix of the rigid mass block and the coupled system,the dynamic decoupling method is used to identify the multi-directional impedance matrix of the rubber isolator.The identified impedance matrix of the rubber isolator agrees well with the test data,which verifies the effectiveness of the dynamic decoupling method.This work provides guidance for the precise modeling of floating raft systems.

vibration and wave;floating raft system;rubber isolator;dynamic decoupling method;multi-directional impedance

O328

：A

：10.3969/j.issn.1006-1335.2016.06.037

1006-1355(2016)06-0186-06

2016-07-25

孫巍（1978-），男，浙江省紹興市人，碩士，從事艦船設(shè)計(jì)與建造研究。E-mail:sunwei1313@sina.com