基于EMD分解和集對分析的風電功率實時預測

楊 茂 陳郁林

(東北電力大學電氣工程學院 吉林 132012)

?

基于EMD分解和集對分析的風電功率實時預測

楊 茂 陳郁林

(東北電力大學電氣工程學院 吉林 132012)

風電功率時間序列的隨機性和波動性使得風電功率多步預測時難以達到理想的預測準確度，因此，提出一種基于經驗模態分解(EMD)和集對分析的風電功率實時預測模型。該模型首先將風電功率時間序列經EMD分解，處理成有限個相對平穩的分量；然后利用極值點劃分法，按波動程度相近的原則將分量重構為高頻、中頻和低頻3個分量；最后對3個分量各自的特點針對性地建立預測模型，并將3個分量的預測結果疊加作為原始風電功率的預測值，用滾動的方式實現多步預測。采用3個不同裝機容量的風電場的實測風電功率數據進行仿真，結果表明該方法提高了多步預測的準確度，顯示出了良好的預測性能。

風電功率 實時預測 經驗模態分解 秩次集對分析

0 引言

風電作為清潔能源已受到越來越多的關注，因此風力發電技術得到了長足的發展，技術相對比較成熟，市場競爭力也越來越強[1]。然而，風力發電的間歇性、隨機性和波動性等特點使得風電的安全并網受到嚴峻的挑戰，并且大規模風電并網后給電力系統的穩定運行帶來很多不利影響，這些問題使風力發電的發展受到制約[2]。為解決這些問題，人們提出了一些方法，比如，增加風電機組的裝機容量以及常規機組的備用容量，以減小風電功率波動對電網運行的影響，但這大大增加了系統運行的費用，經濟性較差。目前比較常用的方法是對風電功率進行準確預測，實現對電網調度的有效控制，解決問題的同時也保證了經濟性。

風電功率預測方法可以分為兩大類，即物理方法和統計方法。物理方法一般基于數值天氣預報先對風速進行預測，然后根據功率曲線得到風電功率的預測值，這種方法的預測時間范圍相對較長[3，4]。統計方法則是基于歷史數據對風速和功率等進行預測。由于數值天氣預報模型很難獲得，而歷史數據的獲取比較容易，因此，目前統計方法在風電功率預測中的應用比較廣泛。比較常用的統計方法有持續法[5]、時間序列法[6]、人工神經網絡法[7]、支持向量機法[8]、模糊邏輯法[9]以及這些方法的組合方法[10]等。

風電功率預測根據預測范圍還可以分為短期預測(6 h以內)、中期預測(6～24 h)和長期預測(1～7天)。國家能源局文件[11]風電場功率預測預報管理暫行辦法中規定了一種實時預測，即對未來15 min～4 h的風電功率進行時間分辨率為15 min的預測預報。實時預測實質上是超短期多步預測。對風電功率進行準確的實時預測，能夠為電網調度控制和運行方式的制定提供可靠的支持，從而降低風電功率特性對電網的不利影響。然而，大多數方法在單步預測的過程中都表現良好，但當外推到多步預測時，預測準確度往往無法滿足要求。而且，單一的方法一般無法對隨機性較強的風電功率進行準確預測。因此，將隨機多變的原始風電功率序列預先進行處理，提取變化規律相近的特征信息進行組合，然后根據不同特征信息的特點分別建立相應的多步預測模型，將有望提高多步預測的準確度。

基于上述分析，本文提出一種基于經驗模態分解(Empirical Mode Decomposition，EMD)分解和集對分析相結合的風電功率實時預測模型。應用EMD分解技術[12]將風電功率分解成相對平穩的分量序列，然后采用極值點劃分法將這些分量按照其變化規律分為高頻、中頻和低頻3類分量。然后，利用不同的預測方法對3類分量進行預測。最后，將3個分量的預測結果疊加作為風電功率的預測值，用滾動的方式實現多步預測。

本文采用多個風電場對所提出的方法進行測試，并且針對某一風電場進行了多日預測。預測結果表明，本文所提出的方法在多步預測中預測準確度高于一般方法，顯示出了良好的預測性能。

1 EMD分解基本原理

經驗模態分解是一種基于信號自身的時間尺度的分解方法，由美籍華人N.E.Huang等于1998年提出。該方法無須預先設定任何基函數，是一個有限次濾波的過程，與傅里葉變換和小波分解等方法有著本質性的差別。EMD方法的這些特點使其在處理非線性非平穩信號上具有明顯的優勢。因此，適合將EMD方法用于處理隨機波動的風電功率序列。

待分析信號經過EMD分解處理，得到有限個不同尺度或趨勢的固有模態函數(Intrinsic Mode Function，IMF)分量，各個分量包含了原信號的不同時間尺度和特征信號，與原始數據相比具有更強的平穩性和規律性。分解得到的固有模態函數必須滿足兩個條件：①函數在整個時間范圍內，局部極值點和過零點的數目必須相等，或最多相差一個；②在任意時刻點，局部最大值的包絡(上包絡線)和局部最小值的包絡(下包絡線)平均必須為零[13]。

EMD分解過程比較簡單，具體過程如下：

1)找出X(t)(原始信號)中所有的極大值點和所有極小值點，利用三次樣條差值函數擬合出兩條包絡線。

2)求出上包絡線和下包絡線的均值m(t)。

3)用原始序列減去其上下包絡線的均值m(t)得到新的序列c(t)，即c(t)=X(t)-m(t)。

4)判斷c(t)是否滿足IMF條件：如果滿足條件，則將c(t)分離出來，得到剩余分量r(t)，即r(t)=X(t)-c(t)；如果不滿足條件，則將c(t)作為新的信號，重復步驟1)～步驟3)，直到c(t)滿足IMF條件為止。

5)將得到的r(t)作為新的原始序列，重復步驟1)～步驟4)，最終得到有限個IMF分量和一個剩余分量。

經過上述過程，將隨機波動的信號分解為若干個平穩的IMF分量和一個剩余分量(平均趨勢或常數)，表示為

(1)

2 秩次集對分析在預測中的應用

集對分析[14]是一種不確定性分析理論，在應用時，首先將具有某種關系的兩個集合構成集對，然后通過某種方法對兩個集合的N個特性進行同一性、差異性和對立性分析，以此建立同異反聯系度，集對分析聯系度的表現形式一般為

(2)

式中，S為集對共同具有的特性個數；P為集對相互對立的特性個數；F為介于共同和對立之間的特性個數；N為特性的總數，N=S+F+P；j為對立度系數，取值一般為-1；i為差異度系數，i∈[-1,1]， 它是宏觀與微觀兩個層次相互結合的參量，有時僅起到標記作用。

建立聯系度是應用集對分析的關鍵，通過建立聯系度，將事物之間的確定和不確定性關系聯系到一起，從而進行不確定性分析。

秩次集對分析[15]實質上是利用秩次的概念建立集對之間聯系度的一種集對分析方法。秩次，即元素在集合中相對大小的位次。例如，有集合B=(1，8，3，6)，那么與之相對應的秩次集合為B′=(1，4，2，3)。因此，在進行秩次集對分析時，要對集合進行秩次變換，構成秩次集對，根據秩次集對的秩次對應關系分析出原始集對的同一性、差異性和對立性，從而得到原始集對的聯系度。

基于集對分析的時間序列預測實質上是一種相似性預測[16，17]，其具體步驟如下：

設時間序列x1,x2,…,xn， 且xi和m個相鄰的歷史值xi-1,xi-2,…,xi-m有關。

1)滑動生成集合Bi=(xi,xi+1,…,xi+m-1)(i=1,2,…,n-m)， 并保留每個集合的后續值xi+m。

2)將集合Bn+1=(xn-m+1,xn-m+2,…,xn-1,xn)與Bi分別建立秩次集對，進行秩次集對分析，建立聯系度。

3)根據聯系度最大原則找出與Bn+1最相似的集合Bk，將Bk的后續值作為xn+1的預測值。

風電功率序列變化趨勢是建立歷史數據與預測數據之間關系的重要依據，而文獻[18]也表明，風電功率時間序列中存在一定的日周期性分量，而經EMD分解后的IMF分量也呈現出了一定的周期規律。由于秩次集對分析是一種反映時間序列的變化趨勢的相似性分析方法，因此，在預測時長較短的實時預測中，應用秩次集對分析對風電功率序列進行預測，有望提高預測準確度。

3 基于EMD和集對分析的風電功率實時預測模型

風電功率時間序列具有較強的間歇性和波動性，因此在進行多步預測[19，20]時，單一的方法難以達到理想的預測準確度?，F有的大多數預測方法在進行多步預測時，其對于相對平穩的時間序列的預測準確度往往很高，而波動性比較明顯的時間序列由于其變化規律很難掌握，所以對其預測時，準確度往往很低。由于EMD分解方法可將波動性較強的時間序列分解成相對平穩的序列，在非平穩數據處理中體現了突出的優勢。因此，本文提出了一種基于EMD和集對分析相結合的風電功率實時預測模型。

應用EMD分解時，原始時間序列經EMD分解后，得到有限個固有模態分量(IMF)。然而由于數據的平穩程度不同，所以隨著數據的變化，得到的IMF分量的個數會產生變化。如果對每一個分量都進行預測，然后重構得到預測結果，則變化的分量個數勢必會增加預測的難度。而且預測一定會產生誤差，多個分量誤差經過累加，必然會導致預測誤差的增大。因此，將分量根據平穩程度劃分后進行重構，使重構后的分量所包含的特征信息集中，并且將不同分量之間的影響隔離開來，從而使預測對象減少，這樣做有望在降低建模難度的同時提高預測準確度。

由于EMD分解后的IMF分量是一個以y=0為軸上下波動的時間序列，其整體不存在上升或者下降的趨勢，因此IMF分量的波動次數在很大程度上反映了它的波動程度。因此，本文提出一種極值劃分方法對分解得到的IMF分量進行波動程度分類。極值劃分方法即求出所有IMF分量的極大值和極小值的個數，極值的個數反映了分量的波動次數，以此來刻畫分量的波動程度，根據極值的個數按高、中、低頻劃分IMF分量，將分類后的分量重構為高、中、低頻3個分量。

重構后的3個分量的波動程度不同，而且各分量有不同的特征信息和變化規律，所以需要根據各自的特點采用不同的方法進行預測，以提高預測準確度。

由于高頻分量的波動性和隨機性仍然比較明顯，序列變化劇烈，無明顯規律可言，因此本文對高頻分量采用對隨機過程描述較好的、速度較快的AR時間序列預測模型進行預測。由于構成中頻和低頻分量的IMF分量相對比較平穩，而且呈現出了一定的周期規律，因此對中頻和低頻分量采用相似性預測效果較好的集對分析預測模型進行預測。然后將各個分量的預測值進行重構，得到原始序列的預測值。

目前，多步預測方式大體可分為3種，分別為一次多步預測(即一次性向后預測多步的預測方式)、滾動多步預測和多采樣尺度多步預測。應用多采樣尺度方式進行多步預測時，由于采樣尺度拉大后，序列數之間的關聯程度變弱，而且難以利用與待預測點相連的相關程度明顯的數據，所以多步預測結果往往難以令人滿意。對于一次多步預測和滾動多步預測方式而言，由于本文在進行中頻和低頻分量預測時采用的是集對分析預測模型，集對分析預測時將后續值作為預測值，其對具有一定周期性的時間序列向后一步預測準確度較高，而滾動預測實質上是一種多次單步預測，每一次預測時都得到準確度較高的預測值，則向后預測值偏離真實值的程度將有望減小。因此，本文采取滾動的方式進行多步預測。具體建模步驟如下：

1)原始風電功率序列X經EMD分解后得到有限個IMF分量。

2)利用極值劃分方法將分解得到的IMF分量按波動程度分為高頻、中頻和低頻3類，并將各類分量重構得到3個分量，分別為高頻分量R1、中頻分量R2和低頻分量R3。

3)利用AR時間序列預測模型對高頻分量進行預測，得到預測值x1，利用秩次集對分析預測模型對中頻和低頻分量進行預測，得到預測值x2和x3。

4)將各個分量的預測值進行重構疊加，得到原始風電功率序列的預測值x，即x=x1+x2+x3。

5)將預測值x加入原始序列構成新序列X(t+1)。

6)取X(2)～X(t+1)作為新的原始序列X，重復執行步驟1)～步驟6)，直到達到預測步數為止。

算法結構圖如圖1所示。

圖1 實時預測結構圖Fig.1 The model structure of real-time prediction

4 仿真實驗與結果分析

4.1 數據來源

本文選擇3個風電場某月的風電功率數據作為算例，以整場輸出的總功率為研究對象，采樣間隔為15 min。3個電場的裝機容量見表1。

表1 風電場裝機容量Tab.1 The installed capacity of wind farms

本文以風電場B作為主要研究對象，將多個不同裝機容量的風電場的預測結果進行比較，以驗證本文方法的普適性。

4.2 評價指標

本文采用國家能源局文件風電場功率預測預報管理暫行辦法中的評價指標：日平均預測計劃曲線準確率r1、日平均預測計劃曲線合格率r2、全天預測結果均方根誤差r3來對預測的結果進行衡量。下面給出各個指標的形式。

日平均預測計劃曲線準確率r1

(3)

(4)

日平均預測計劃曲線合格率r2

(5)

(6)

(7)

(8)

式中，r2i為第i次實時預測的合格率。

全天預測結果方均根誤差r3為

4.3 仿真實驗

以裝機容量為265.5 MW的風電場B為例對本文模型進行測試，取某月風電功率序列(共2 880個采樣點)如圖2所示。

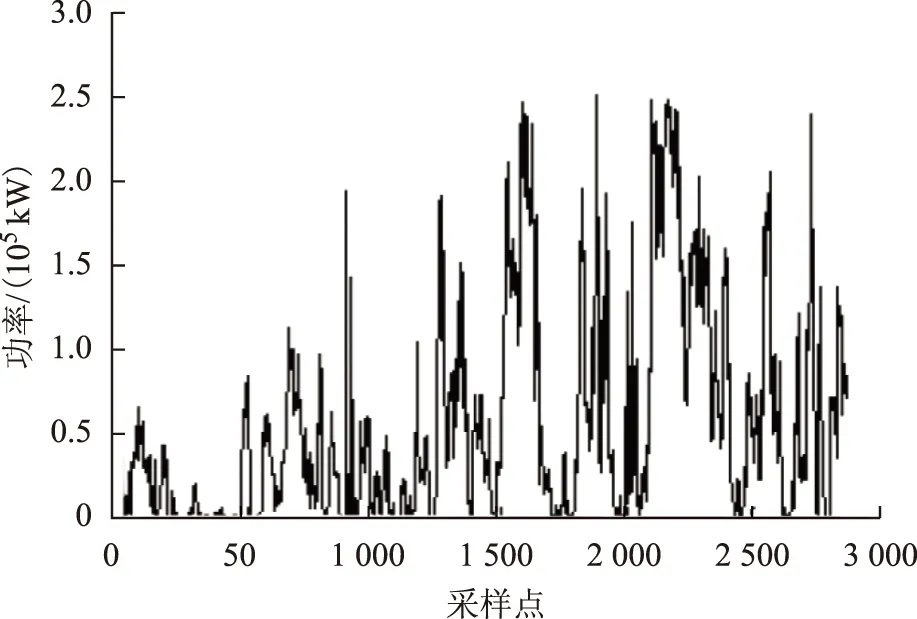
圖2 風電場B某月風電功率序列Fig.2 A month of wind power sequence of wind farm B

本文方法建模域長度為1 000，即用某點前1 000個點的序列預測該點及以后的16個點(實時預測)。以預測起始點為1 920為例，預測1 921～1 936點的風電功率。圖3給出了建模域1 000個點(921～1 920)的原始風電功率序列。

圖3 建模域原始風電功率序列Fig.3 The original wind power sequence of modeling domains

將建模域序列經EMD分解后，共生成8個IMF分量(C1～C8)和一個剩余分量r9，如圖4所示。

圖4 建模域EMD結果Fig.4 The EMD result of modeling domains

從圖4中可以看出，分解得到的IMF分量與建模域原始風電功率序列相比平穩很多。

然后計算每個分量的極值點的個數，結果見表2。

表2 各分量極值點個數Tab.2 The number of extreme points of C1～C8 and r9

選擇一個合適的n作為區分高頻分量和中頻分量的閾值，本文選擇n=30。所以，C1～C4為高頻分量，疊加重構后得到R1，C5～C8為中頻分量，疊加重構后得到R2，剩余分量r9作為低頻分量R3。重構結果如圖4所示。將重構后的3個分量分別用不同的方法進行預測，并將各分量的預測結果疊加后作為原始風電功率預測的結果。圖5給出了重構后的功率曲線圖。

圖5 重構結果Fig.5 The reconstruction components of wind power series

采用EMD分解方法對風電功率進行實時預測還有其他兩種方式，一種為經EMD分解后不進行重構，直接對分解后的每個分量分別預測，疊加得到預測值，并采用滾動的方式實現實時預測的模型(EMD_N)；另一種為經EMD分解，用極值點劃分法重構后，不采用滾動生成多步預測的方法，而是采用一次多步預測的方式，即每個分量一次性向后預測16個點，將預測值對應疊加一次性得到原始風電功率實時預測結果的模型(Disposable EMD，D_EMD)。

為了驗證本文方法的有效性，本文分別采用EMD_N模型和D_EMD模型以及應用比較廣泛的AR模型對相同風電功率進行了預測，得到4天的預測結果見表3。

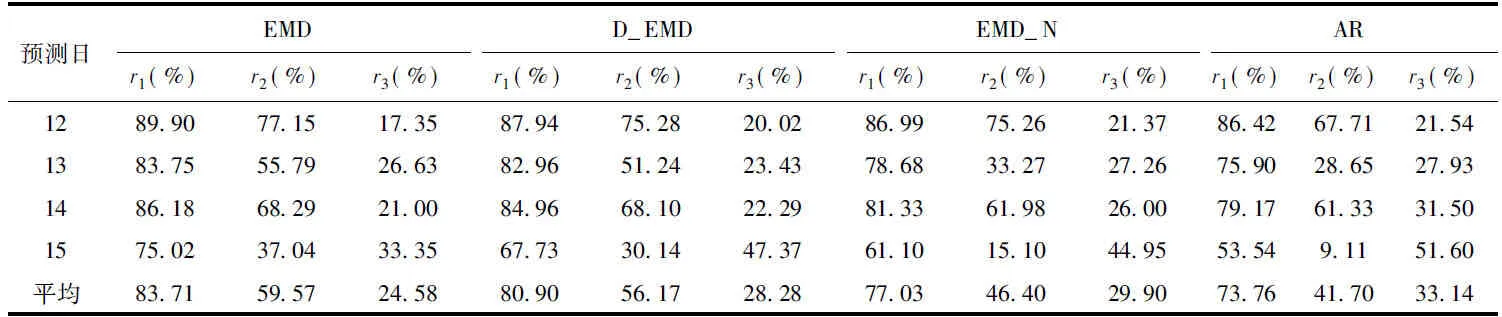
表3 不同模型的實時預測結果Tab.3 The results of real-time prediction with different models

從表3中可以看出，本文所提出的模型(EMD)以及D_EMD模型的實時預測結果全面優于AR模型的預測結果；EMD_N模型略優于AR模型。表明EMD分解能有效降低波動性對預測結果的影響，從而提高預測的準確度。

EMD模型以及D_EMD模型的實時預測結果全面優于EMD_N模型，表明經EMD分解并重構后進行預測的方式預測性能更具優越性。

EMD模型與D_EMD模型相比，準確率r1和合格率r2較D_EMD模型普遍有所提高，說明了本文模型采用滾動多步預測方式優于一次多步預測方式。

從表3中還可以看出，不同預測日的預測準確率不同，預測日15的準確率最低，這是由于每日的風電功率波動不同造成的，預測日15的波動程度最大，所以該日的預測準確率偏低，這種由于時間序列波動性明顯而造成預測準確率下降的現象比較普遍，如何提高波動性明顯的時間序列預測的準確率，目前仍然是個難題，需要進一步研究。常規的AR方法在該日的準確率只有53.54%，合格率只有9.11%，但是，本文所提模型在該日的準確率有了大幅提高，達到

75.02%，相比于AR方法最多提高了21.48%。因此，本文所提出的模型在變化比較明顯的風電功率序列預測中預測性能比較突出。圖6給出了4種方法在某個點實時預測的效果圖。從圖中也可以看出，本文所提出的方法優于其他3種方法。

圖6 各種預測方法預測效果圖Fig.6 The real-time prediction pattern of all method

為了進一步驗證本文方法的有效性，本文還選擇了另外兩個不同裝機容量的風電場的風電功率數據進行預測，4種方法的預測結果見表4。

表4 不同風電場的實時預測結果Tab.4 The results of real-time prediction with different wind farms

從表4中可以看出，裝機容量不同的風電場在采用四種方法進行實時預測時，本文所提出的方法在準確率、合格率和全天預測結果方均根誤差方面都優于其他3種模型，展示出了良好的多步預測性能。綜上所述，該模型具有一定的實用價值。

5 結論

風電功率序列由于具有間歇性、隨機性和波動性，因此在對風電功率進行多步預測時難以達到理想的預測準確度。為此，本文提出了一種基于EMD分解和秩次集對分析的風電功率實時預測模型，用某風電場的風電功率數據對模型進行了驗證。并對3個不同裝機容量的風電場的預測結果進行了對比。結果表明：

1)本文所提出的基于EMD分解和秩次集對分析的風電功率實時預測模型與D_EMD模型、EMD_N模型以及常規模型AR預測模型相比，預測準確度有了很大的提高，尤其在波動程度較大的預測日，預測準確度最多提高了21.48%，展示出了優越的實時預測性能，多個風電場的預測結果的對比也得出了相同的結論。

2)將原始風電功率序列進行EMD分解，得到相對平穩的IMF分量，再對IMF分量進行預測，降低了波動性對實時預測結果的影響。

3)對EMD分解得到的IMF分量進行重構，得到3個特征信息比較集中且相對平穩的分量，然后再對這3個分量針對性地建模，最終疊加得到預測結果。實驗表明，對IMF分量進行重構，不但節約了預測成本，而且降低了由于模型過多造成的預測誤差累積，從而使得預測準確度大幅提高。

但是，在波動性較強的時段，預測準確度不夠理想，仍有待提高。

[1] 薛禹勝，雷興，薛峰，等.關于風電不確定性對電力系統影響的評述[J].中國電機工程學報，2014，34(29)：5029-5040. Xue Yusheng，Lei Xing，Xue Feng，et al.A review on impacts of wind power uncertainties on power systems[J].Proceedings of CSEE，2014，34(29)：5029-5040.

[2] 楊錫運，孫寶君，張新房，等.基于相似數據的支持向量機短期風速預測仿真研究[J].中國電機工程學報，2012，32(4)：35-41. Yang Xiyun，Sun Baojun，Zhang Xinfang，et al.Short-term wind speed combined prediction for wind farms based on wavelet transform[J].Proceedings of CSEE，2012，32(4)：35-41.

[3] Cuo Lan，Zhang Yongxin，Wang Qingchun，et al.Climate change on the northern Tibetan Plateau during 1957-2009：Spatial patterns and possible mechanisms[J].Journal of Climate，2013，26(1)：85-109.

[4] 王麗婕，冬雷，高爽.基于多位置NWP與主成分分析的風電功率短期預測[J].電工技術學報，2015，30(5)：79-84. Wang Lijie，Dong Lei，Gao Shuang.Wing power short-term prediction based on principal component analysis of NWP of multiple locations[J].Transactions of China Electrotechnical Society，2015，30(5)：79-84.

[5] 李麗，葉林.基于改進持續法的短期風電功率預測[J].農業工程學報，2010，26(12)：182-187. Li Li，Ye Lin.Short-term wind power forecasting based on an improved persistence approach[J].Transactions of the Chinese Society of Agricultural Engineering，2010，26(12)：182-187.

[6] 冬雷，王麗婕，郝穎，等.基于自回歸滑動平均模型的風力發電容量預測[J].太陽能學報，2011，32(5)：617-622. Dong Lei，Wang Lijie，Hao Ying，et al.Prediction of wind power generation based on autoregressive moving average model[J].Acta Energiae Solaris Sinica，2011，32(5)：617-622.

[7] 羅毅，劉峰，劉向杰.基于主成分—遺傳神經網絡的短期風電功率預測[J].電力系統保護與控制，2012，23(40)：47-53. LuoYi，Liu Feng，Liu Xiangjie.Short-term wind power prediction based on principal component analysis and genetic neural network[J].Power System Protection and Control，2012，23(40)：27-53.

[8] 王賀，胡志堅，仉夢林.基于模糊信息粒化和最小二乘支持向量機的風電功率波動范圍組合預測模型[J].電工技術學報，2014，29(12)：218-224. Wang He，Hu Zhijian，Zhang Menglin.A combined forecasting model for range of wind power fluctuationbased on fuzzy information granulation and least squares support vector machine[J].Transactions of China Electrotechnical Society，2014，29(12)：218-224.

[9] 楊茂，熊昊，嚴干貴，等.基于數據挖掘和模糊聚類的風電功率實時預測研究[J].電力系統保護與控制，2013，41(1)：1-6. Yang mao，Xiong Hao，Yan Gangui，et al.Real-time prediction of wind power based on data mining and fuzzy clustering[J].Power System Protection and Control，2013，41(1)：1-6.

[10]楊茂，賈云彭，錢為，等.基于動態權重的風電功率組合預測方法研究[J].東北電力大學學報，2013，33(1-2)：131-136. Yang Mao，Jia Yunpeng，Qian Wei，et al.A combination method research for wind power predication based on dynamic weight[J].Journal of Northeast Dianli University，2013，33(1-2)：131-136.

[11]國家能源局.風電廠功率預測預報管理暫行辦法[S].北京：國家能源局，2011.

[12]劉興杰，米增強，楊奇遜，等.一種基于EMD的短期風速多步預測方法[J].電工技術學報，2010，25(4)：165-170. Liu Xingjie，Mi Zengqiang，Yang Qixun，et al.A novel multi-step prediction for wind speed based on EMD[J].Transactions of China Electrotechnical Society，2010，25(4)：165-170.

[13]Huang N E，Shen Z，Long S，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London Series A，1998，454：903-995.

[14]趙克勤.集對分析及其初步應用[J].大自然探索，2000，13(1)：4-8. Zhao Keqin.Set pair analysis and its preliminary application[J].Exploration of Nature，2000，13(1)：4-8.

[15]汪明武.集對分析耦合方法與應用[M].北京：科學出版社，2014.

[16]高潔，盛昭瀚.集對分析聚類預測法及其應用[J].系統工程學報，2002，17(5)：458-462. Gao Jie，Sheng Zhaohan.Method and application of set pair analysis classified prediction[J].Journal of Systems Engineering，2002，17(5)：458-462.

[17]郭鈺鋒，孫頔，于繼來，等.集對分析理論在風電場風速區間預測中的應用[J].電力系統自動化，2014，38(2)：6-11. Guo Yufeng，Sun Di，Yu Jilai，et al.Application of set pair analysis in wind speed interval prediction for wind farms[J].Automation of Electric Power Systems，2014，38(2)：6-11.

[18]楊茂，王東，嚴干貴，等.風電功率波動特性中的周期性研究[J].太陽能學報，2013，34(11)：2020-2026. Yang Mao，Wang Dong，Yan Gangui，et al.study on periodicity for wind power fluctuations characteristics[J].Acta Energiae Solaris Sinica，2013，34(11)：2020-2026.

[19]嚴干貴，王東，楊茂，等.兩種風電功率多步預測方式的分析及評價[J].東北電力大學學報，2013，33(增1)：126-130. Yan Gangui，Wang Dong，Yang Mao，et al.The analysis and evaluation of two ways for multi-step wind power prediction[J].Journal of Northeast Dianli University，2013，33(S1)：126-130.

[20]楊茂，孫涌，孫兆鍵，等.風電場大規模數據管理系統設計與研發[J].東北電力大學學報，2014，34(2)：27-31. Yang Mao，Sun Yong，Sun Zhaojian，et al.Design and development of large-scale data management system of wind farm[J].Journal of Northeast Dianli University，2013，34(2)：27-31.

E-mai：yangmao820@163.com(通信作者)

陳郁林 男，1992年生，碩士研究生，研究方向為風力發電技術。

E-mai：bufucisheng0805@163.com

Real-Time Prediction for Wind Power Based on EMD and Set Pair Analysis

Yang Mao Chen Yulin

(School of Electronic Engineering Northeast Dianli University Jilin 132012 China)

The randomness and volatility of wind power time series make it difficult to achieve the desired multi-step prediction accuracy.Therefore, a model of real-time prediction for wind power based on empirical mode decomposition(EMD) and set pair analysis is presented.The proposed wind power sequences are firstly decomposed into a series of functions with more stationary variation by the EMD technique.Then these functions are divided into three components(high-middle-low frequency components) according to their run-lengths by the extreme point division method.Finally, three prediction models are built under the basis of their respective variation rules, and the results of three prediction models are reconstructed with the original wind power prediction value, this model achieves multi-step prediction by rolling prediction.The data from Three different wind farms with different installed capacity are used for simulate experiment.The results show that the proposed approach possesses with higher accuracy and the prediction performance is satisfied.

Wind power，real-time prediction，empirical mode decomposition(EMD)，rank and set pair analysis

國家重點基礎研究發展計劃(973計劃)(2013CB228201)、國家自然科學基金(51307017)、吉林省產業技術研究與開發專項(2014Y124)和國家留學基金資助。

2015-06-26 改稿日期2015-08-28

TM614

楊 茂 男，1982年生，副教授，研究方向為風力發電技術。