圓形空心墩日照溫度場Laplace變換解析計算*

趙 亮 楊志勇 張亮亮

(武漢理工大學土木與建筑工程學院1) 武漢 430000) (重慶大學土木工程學院2) 重慶 404100)

圓形空心墩日照溫度場Laplace變換解析計算*

趙 亮1)楊志勇1)張亮亮2)

(武漢理工大學土木與建筑工程學院1)武漢 430000) (重慶大學土木工程學院2)重慶 404100)

為研究混凝土圓形空心墩的日照溫度分布及變化特征，建立了日照作用下空心墩瞬態熱傳導問題的數學模型.利用氣象參數描述邊界條件，采用Laplace變換，將時間域的問題轉換成Laplace域上的問題，利用Stehfest數值反演得到時間域的解答，從而得到溫度場的解析計算式.編程計算得到溫度場，與實驗測得結果進行對比，兩者的溫度變化趨勢基本一致，結果吻合較好.氣象參數分析表明太陽輻射、風速、日平均氣溫，以及日溫度變化幅度是影響混凝土空心墩的溫度分布的主要因素.

混凝土圓形空心墩；日照溫度場；解析方法；Laplace積分變換

0 引 言

混凝土空心墩可以節省材料、減輕自重并降低對地基強度的要求，因而得到較廣泛的應用.處于自然環境中的橋梁，在長時間的日照作用下，空心墩內外壁面溫差較大，分布不均勻，產生的溫度應力不可忽視[1-2].

關于空心墩的日照溫度場和溫度效應，自上世紀60年代以來，不少學者做了大量的研究.蔣國富等[3-5]分別基于現場實測資料，推導了適合橋梁所在地區的混凝土薄壁空心墩沿壁厚方向的溫度梯度模式.胡安慶等[6-7]根據實際工程的實測資料編制了溫度場及應力場計算程序，為設計提供了一定的方便和參考.

以上分析對橋墩日照溫度效應的研究具有極大的幫助，但溫度效應問題具有明顯地域性，進行現場時時觀測的難度大；對大量實測數據的處理、以及從計算程序的編制到建模分析都需要花費大量的時間和精力；且這些大多針對某一具體工程的箱型、雙肢型薄壁空心墩等，對圓形空心墩研究相對較少.因此，文中試圖根據熱傳導原理，利用氣象參數[8-9]建立日照作用下圓形空心墩瞬態熱傳導模型，利用Laplace變換及Stehfest數值反演，得到適用于不同橋址地區的混凝土圓形空心橋墩溫度場解析計算方法.同時制作了模型實驗，通過實測溫度數據驗證解析計算結果的有效性和精確性，并對影響空心墩溫度場變化規律的因素進行分析，為設計和施工提供依據和方便.

1 混凝土空心墩溫度場數學模型的建立

1.1 熱傳導方程

大型混凝土空心墩的日照溫度場分布屬于復雜的三維瞬態熱傳導問題，但可近似地認為沿著高度方向溫度呈均勻分布，熱傳導基本沿著徑向進行，因此混凝土空心墩的溫度場可簡化為二維分布、一維熱傳導問題.于是將方位角為θ的空心墩壁面的溫度分布用T(r,t)表示，計算模型幾何尺寸見圖1.

圖1 計算模型

采用極坐標建立熱傳導控制方程

(1)

式中：T=T(r,t)為方位角θ的截面上徑向r處t時刻的溫度，℃；r2，r1分別為內外半徑，m；t為時間，s；a=λ/ρc為導溫系數，m2/s，其中λ為導熱系數，W/(m·K)；ρ為密度，kg/m3；c為比熱容，J/(kg·K).

1.2 初始條件

日照作用下，假定在初始時刻，混凝土空心墩各點具有相同的初始溫度.其初始條件為

T(r,0)=T0

(2)

式中：T0為空心墩的初始溫度，℃.

1.3 邊界條件

橋梁結構表面的日照溫度場問題的傳熱邊界條件復雜且為非線性，若直接采用解析方法求解導熱微分方程是非常困難的，必須進行簡化處理.

不少研究發現太陽輻射過程曲線可利用半正(余)弦波模型模擬為日出到日落期間的半個正(余)弦波.由于氣象臺一般提供水平面上的太陽輻射資料，因此需將水平面上太陽日輻射總量H進行直散分離[10]然后再轉化為豎直面上的太陽輻射量HV[11].在此將筒壁方位角為θ壁面的t時刻太陽輻射強度qV(t)分解為太陽直接輻射qbV(t)和散射及地表反射qdV(t)2部分之和，即

qV(t)=qbV(t)+qdV(t)

(3)

(4)

式中:tk=tsk-trk；ck=0.5(tsk+trk)

其中：下角標k=b時表示與太陽直接輻射相關的參數，k=d時表示與太陽反射和散射相關的參數.tb和td分別為豎直壁面上的日照時間和水平壁面上的日照時間；trb，tsb分別為豎直壁面的日出日沒時間，trd，tsd分別為水平壁面上的起止時刻，計算見文獻[9-11].

圖2給出了按式(3)采用半余弦波模擬豎直面上的太陽輻射的實例，并與理論曲線和按參考文獻[9]采用半正弦波曲線進行對比，從圖2可見，式(3)模擬結果比較理想，簡化了豎直面上任意時刻太陽輻射分布計算表達式，運用更加方便.

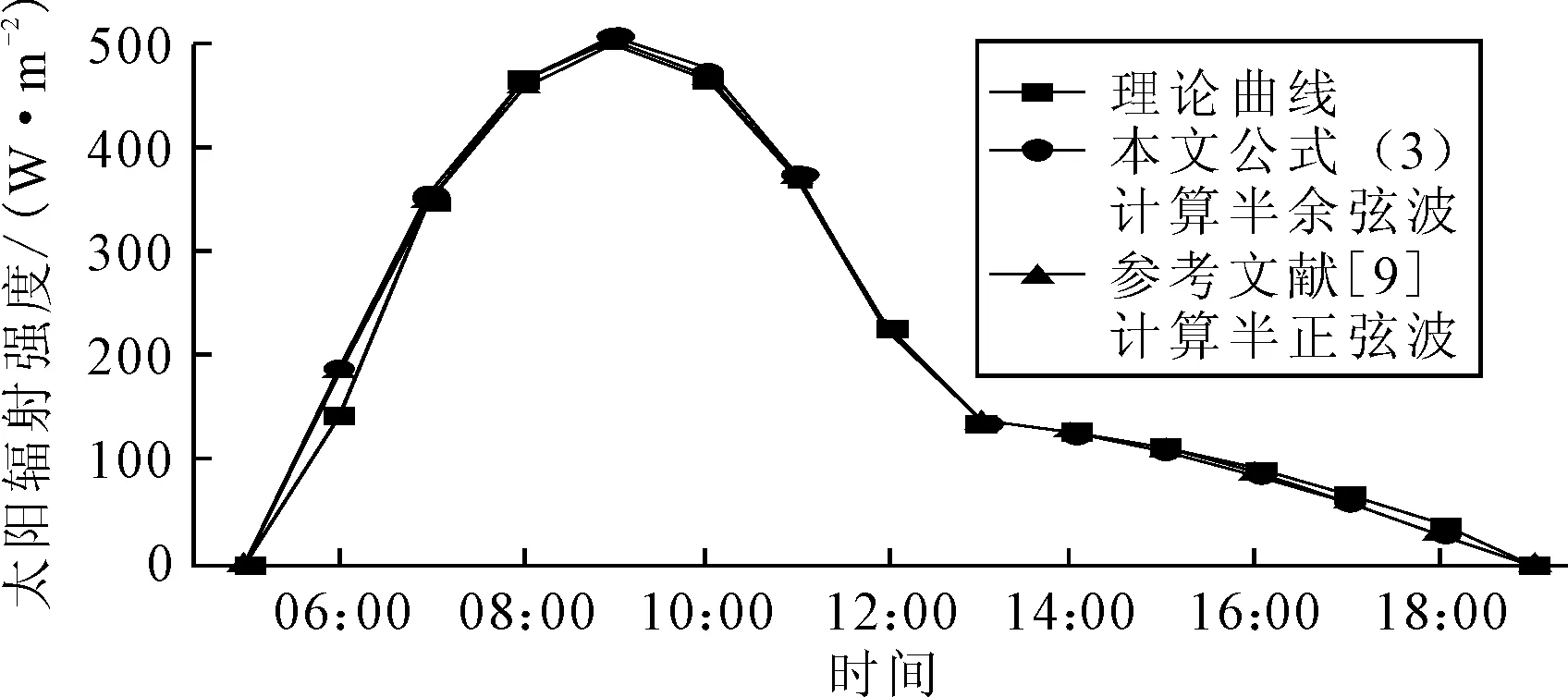
圖2 豎直面上太陽輻射日過程的曲線模擬(日序數181，緯度30.5°，方位角-45°，水平面日輻射總量29.3 MJ/m2)

空心墩外壁與外界的熱交換主要有太陽輻射、對流換熱、輻射換熱.而空心墩內壁，只考對流和輻射換熱，因此空心墩邊界條件為

(5)

為了便于求解計算，將上式展開為傅里葉形式，并寫成復數形式，即

(6)

具體參數如下.

式中：

2 熱傳導方程的求解

2.1 求解

在熱傳導問題中，運用Laplace變換可以消去微分方程中的時間偏導，從而簡化計算.對熱傳導微分方程(1)進行Laplace變換后得

(7)

其通解形式為

式中：J0(·)和Y0(·)分別為第一類、第二類貝塞爾函數；m1，m2為待求系數，由邊界條件確定；s是一個復參量，s=β+iω且ω≥0.

對邊界條件式(6)進行Laplace變化，轉化為s域的象函數方程

(9)

將通解式(8)帶入邊界條件(9)中，整理求解可得

(9)

式中：

2.2 Laplace逆變換的數值計算

由于將得到的頻域解進行逆變換到時間域上的計算復雜且難以實現，因此對Laplace變換采用Stehfest算法[12]進行數值反演，該算法的計算式為

(11)

(12)

式中：t為自變量；N，k，i均為正整數；k=int(0.5i+0.5)；υi為中間函數.

理論上，式(12)中N取值越大，計算精度越高.通過試算，本例中N=30時，效果較好，誤差可控制在10-4～10-6之間.

3 實 驗

3.1 模型參數

混凝土圓形空心墩實驗模型的外徑為3 m，壁厚為0.3 m，采用數字溫度傳感器測量空心墩內外壁溫度.實驗模型及測點布置見圖3～4.計算時間為2013年8月28日，當日氣溫變化28～41 ℃，風速3 m/s.地理緯度30.62°，混凝土吸收率As=0.55.地表短波反射率re=0.2，大氣長波輻射率為εa=0.82，混凝土發射率為ε0=0.9.空心墩外壁向陽面h1=13.58 W/(m2·K)，陰影面h1=11.59 W/(m2·K)；內壁h2=8.3 W/(m2·K).混凝土的熱物性參數見表1.

圖3 試驗模型圖

圖4 測點布置

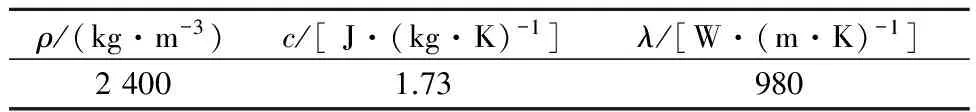
ρ/(kg·m-3)c/[J·(kg·K)-1]λ/[W·(m·K)-1]24001．73980

3.2 溫度場分析

將當地的氣象資料作為輸入參數，利用數學軟件Maple對Laplace逆變換進行反演，得到空心墩各點01:00—24:00的溫度變化計算值，根據實測值與計算值繪制出同一時刻不同方位截面各測點的溫度變化曲線,見圖5.

圖5 計算與實測各測點溫度變化圖

由圖5中可見：

1) 各點的實測溫度變化幅度具有明顯的區別，內壁測點升溫(8 ℃左右)較外壁測點(17 ℃左右)小.受太陽直接輻射強度影響，溫度升幅最大的為測點W1，在17:00后升溫達到最大值46.5 ℃.測點E2在11:00后受太陽輻射最強，達到最大值42.5 ℃.測點N1受到太陽輻射最弱，1 d中的溫度變化幅度最小.同一時刻，不同截面的內外溫差以及空心墩外壁不同測點的溫差均可達到10 ℃.

2) 由于計算中假定初始溫度為均一值，因此日出前，各點計算溫度值基本相同，而實測稍有區別.日出后07:00—10:00間，外壁測點W1，S1，E1，N1的計算值較實測值偏大5%～10%，但各點峰值出現的時刻吻合較好.這是由于采用余弦波模擬太陽輻射強度時，日出后的計算強度值較實際太陽輻射強度大.在15:00—18:00之間，外壁各測點計算值較實測值偏低，這是因為采用余弦波模擬太陽輻射過程中，近似認為各方位角壁面接受的太陽直接輻射在該壁面的cb時刻對稱分布，散射輻射相對于12:00對稱分布.而太陽輻射每日不同時刻實際分布規律不可能如此理想化，尤其夏季，15:00—18:00太陽輻射相對較強，由太陽輻射引起的表面溫度較高，導致此時的計算溫度比實際溫度偏小.

3) 實測溫度變化與計算溫度變化趨勢相似，吻合較好，說明推導的解析計算公式可以用于計算大型混凝土圓形空心墩日照作用下的溫度場.

4 氣象參數對空心墩溫度場的影響

4.1 太陽輻射

以水平面上太陽日輻射總量H為參數，得到了空心墩在不同太陽日輻射總量下，外壁發生最高溫度時刻，橋墩外壁溫度分布(見圖6)以及1 d中內外壁溫差最大值，見圖7.由此可見，太陽輻射量越大，外壁最高溫度值越大，最高溫度增長速度越快.內外壁溫差受太陽輻射影響明顯，輻射量越大，內外壁溫差最大值越大.

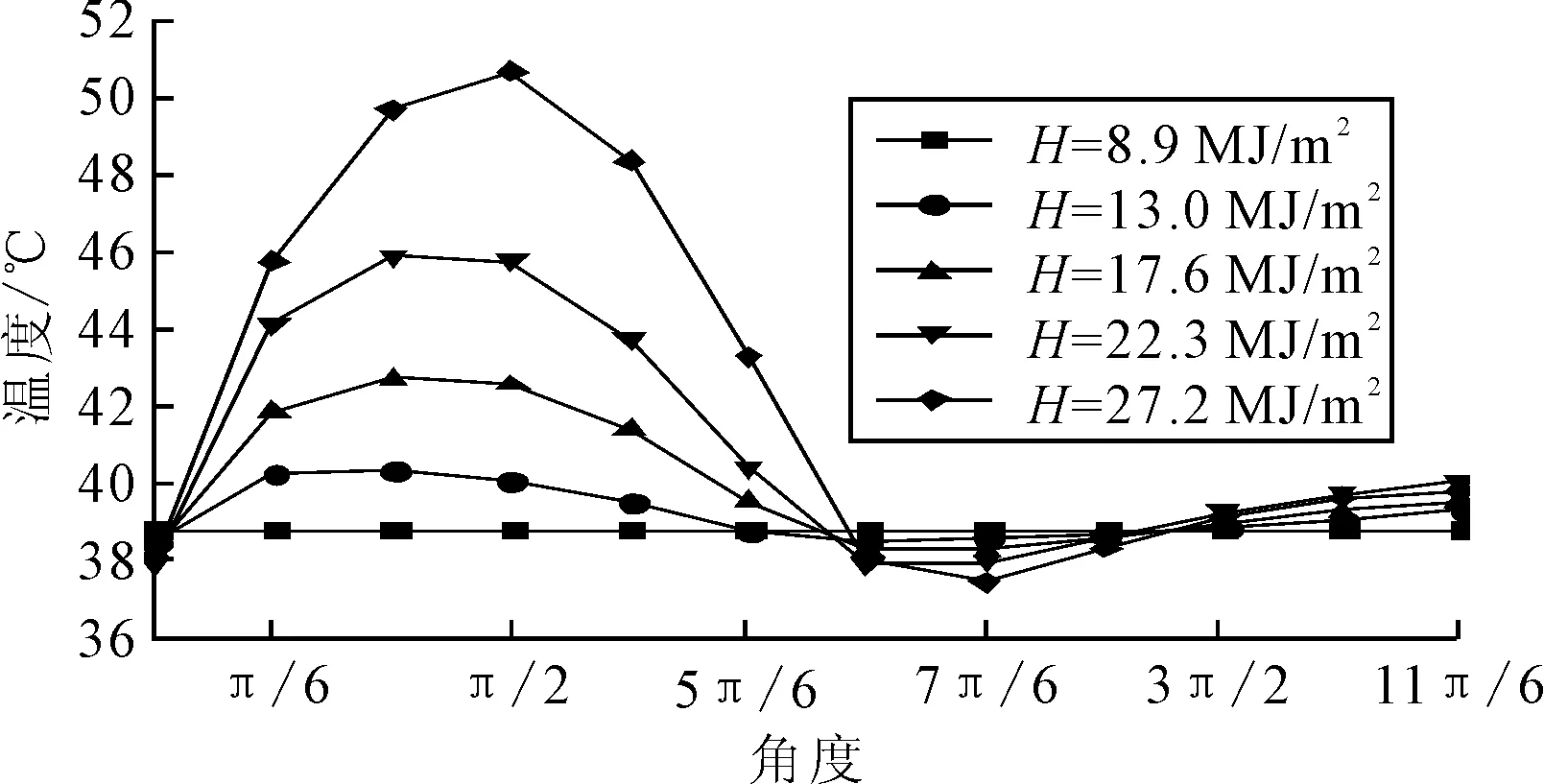
圖6 不同日輻射總量下的外壁最大溫度時刻溫度分布

圖7 日輻射總量對最大內外溫差的影響

4.2 風速

風速大小直接影響空心墩外壁與周圍環境的對流換熱，因此取風速從0～25 m/s之間的6個數值進行對比分析，得到不同風速作用下外壁發生最高溫時刻，橋墩外壁的溫度分布(見圖8)以及內外壁溫差最大值，見圖9.隨著風速的增加，由于對流換熱加快，橋墩表面散熱加強，溫度降低，當風速為0時，橋墩外壁最高溫度達47.8 ℃，內外壁溫差達到最大值10.7 ℃.

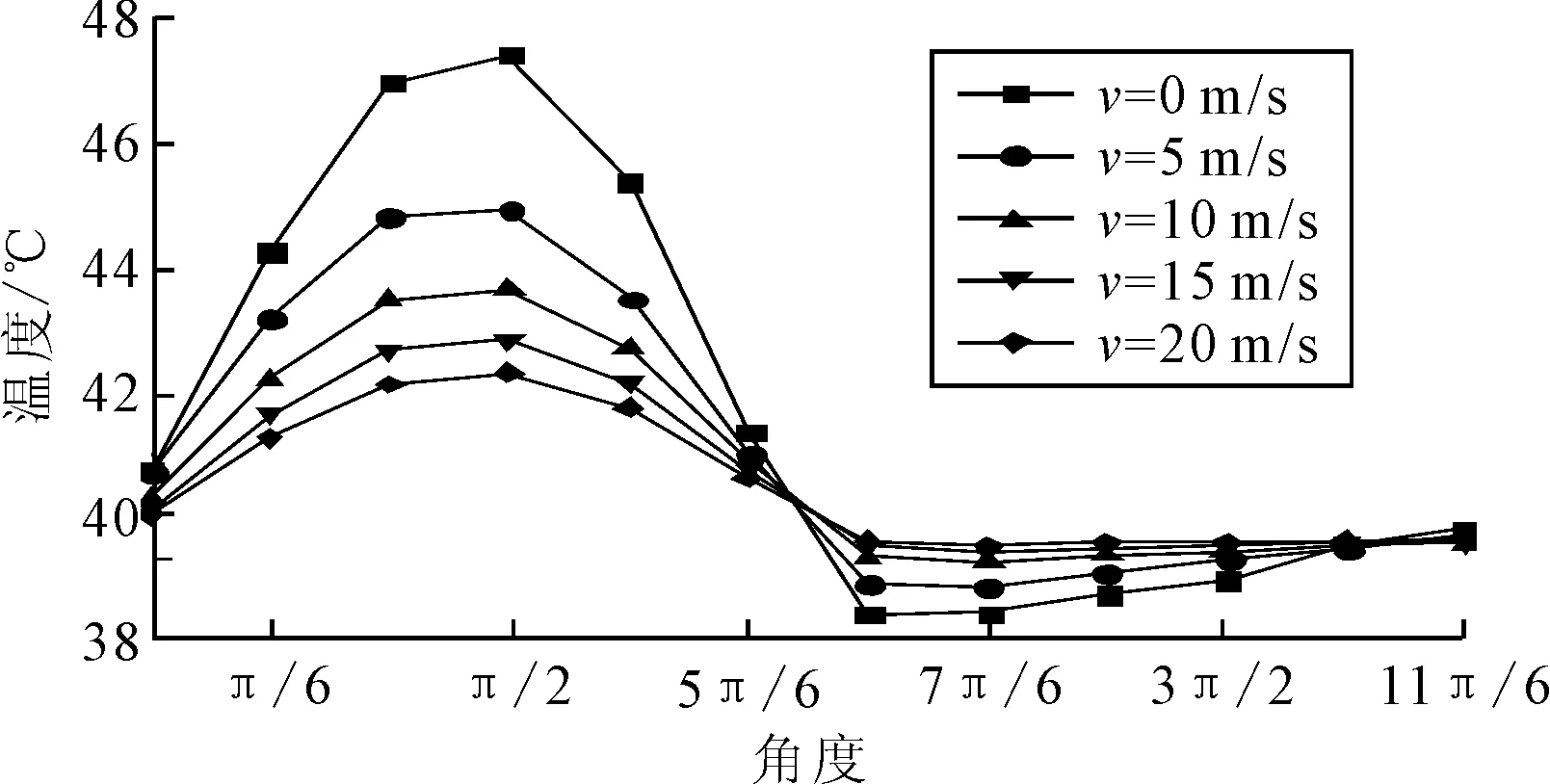
圖8 不同風速下的外壁最大溫度時刻溫度分布

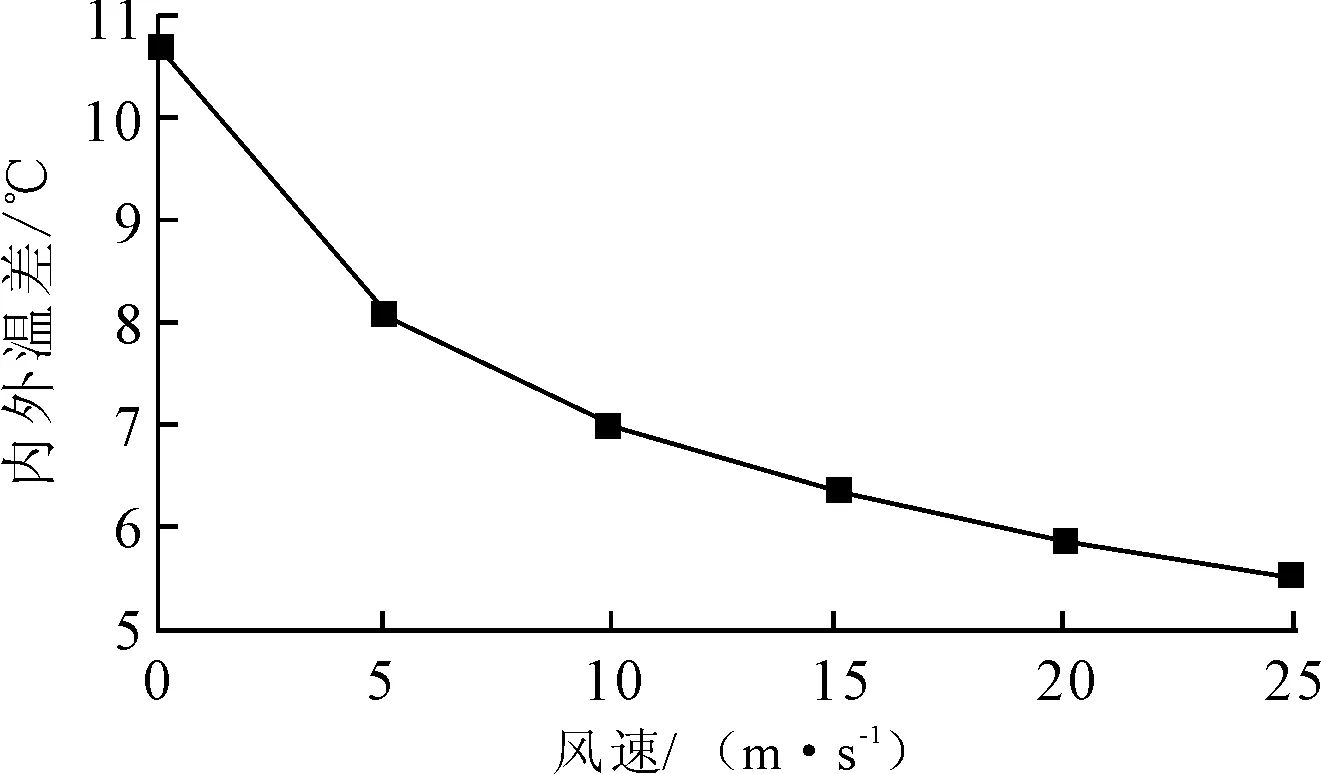
圖9 風速對最大內外溫差的影響

4.3 大氣溫度

混凝土空心墩溫度分布受到外界日氣溫均值和變化幅值的影響.空心墩內部空氣溫度在1 d內變化小，變化幅度僅為2～3 ℃，日平均溫度一般比墩外日平均溫度高3～5 ℃.因此分別取空心墩外大氣日氣溫均值和日幅值為參數，得到空心墩內外溫差最大值見圖10.日氣溫均值和日幅值均對空心墩內外壁溫差影響顯著，日均值越小影響程度越顯著；日幅值越大，內外壁溫差最大值越大.

圖10 日氣溫均值及幅值對最大內外溫差的影響

5 結 論

1) 建立了日照作用下混凝土圓形空心墩的熱傳導方程，采用Laplace變換及逆變換的方法，得到了適用于不同橋址地區的溫度場解析計算方法，對比試驗結果與計算結果，吻合較好.該方法計算簡單，避免了復雜的建模等，可為后期的溫度效應分析提供一定依據和方法.

2) 通過對水平面上的太陽日輻射總量進行直散分離，并轉換為豎直面上的太陽直接輻射和散射與地表反射之和，從而得到的半余弦波曲線，簡化了豎直面上太陽輻射強度函數形式，能更方便較好地模擬太陽輻射.為了便于解析計算，進行了一定的簡化，因而計算值與實測值有一定的偏差.

3) 算例分析表明同一時刻，溫度沿著混凝土空心墩周向和壁厚方向呈現出明顯的非線性，外壁周向溫差可達到10 ℃左右，同時空心墩內外壁溫差最大也可達10 ℃.不同時刻，同一截面由于接受太陽輻射量不同，溫度變化較大.

4) 利用該溫度場解析計算方法可以方便地進行參數分析.氣象參數對比分析發現水平面日輻射總量、風速、日氣溫均值和變化幅度對混凝土空心墩溫度場分布有明顯影響.

[1]劉興法.圓形空心墩日照溫度應力與位移分析[J].鐵道標準設計,1981(3)：14-22.

[2]夏國平,張哲,葉毅.斜拉-懸索協作體系橋的溫度效應分析[J].武漢理工大學學報(交通科學與工程版),2009,33(5)：892-896.

[3]蔣國富.大跨徑橋梁高墩日照溫度效應的研究[D].西安：長安大學,2005.

[4]胡麗華,李德建,陳建平.酉水大橋大跨度連續箱梁橋斜交高墩日照溫度效應分析[J].鐵道科學與工程學報,2013,10(2):23-30.

[5]楊美良,呂尋博,段志岳.山區空心薄壁高墩日照溫度效應[J].長沙理工大學學報(自然科學版),2015(2):29-36.

[6]胡安慶.混凝土矩形空心墩溫度分布研究[D].北京：中國鐵道科學研究院,2010.

[7]張運波,蔡婷婷,劉洋.截面形狀對雙肢薄壁墩溫度場的影響分析[J].鐵道工程學報,2015(3),41-45.

[8]LARSSON O, THELANDERSSON S, PRIESTLEY M J N.Estimating extreme values of thermal gradients in concrete structures[J]. Materials and Structures ACI Journal,2011,44(8):1491-1500.

[9]彭友松.混凝土橋梁結構日照溫度效應研究及應用[D].成都:西南交通大學,2007.

[10]馮巍,董宏,楊柳,等.太陽輻射直散分離模型比較研究-以北京地區為例[J].土木建筑與環境工程,2015,37(1):12-17.

[11]楊金煥，毛家俊，陳中華.不同方位傾斜面上太陽輻射量及最佳傾角的計算[J].上海交通大學學報，2002,36(7):1032-1036.

[12]劉利強.拉普拉斯變換的一種數值算法[J].內蒙古大學學報(自然科學版),2002,21(1):47-49.

Analytical Calculation on Sunshine Temperature Field of Cylindrical Hollow Pier by Laplace Integral Transform

ZHAO Liang1)YANG Zhiyong1)ZHANG Liangliang2)

(SchoolofCivilEngineeringandArchitecture,WuhanUniversityofTechnology,Wuhan430000,China)1)(SchoolofCivilEngineering,ChongqingUniversity,Chongqing404100,China)2)

A mathematical model of transient heat conduction for cylindrical concrete hollow pier is developed to investigate the temperature distribution of large cylindrical concrete hollow pier subjected to the solar radiation. As a first step, the meteorological parameters are used to describe the boundary conditions. Furthermore, the Laplace transform method is adopted to develop the analytical method for the temperature field of the hollow pier. Consequently, the calculation is transformed from time domain to Laplace domain. Then, the solution in Laplace domain is inversely transformed to time domain by Stehfest inversion. In order to comply with the calculation of the temperature field, a mathematical software Maple is adopted to implement the analytical method. Furthermore, the temperature field obtained with the analytical tool is verified with the measured data. Finally, the meteorological parameter analysis shows the solar radiation, wind speeds as well as air temperatures are the main factors effecting the temperature distribution in the cylindrical concrete hollow pier.

cylindrical concrete hollow pier; sunshine temperature field; analytical method; Laplace integral transform

2016-11-01

*重慶市建委項目資助(2014-4-3)

U443.22

10.3963/j.issn.2095-3844.2016.06.013

趙亮(1983—)：女，博士生，主要研究領域外結構溫度效應