基于累積塑性損傷的Q345鋼疲勞裂紋擴展的過載效應研究*

李逸候 楊 平 董 琴

(武漢理工大學交通學院1) 武漢 430063) (高性能船舶技術教育部重點實驗室2) 武漢 430063)

基于累積塑性損傷的Q345鋼疲勞裂紋擴展的過載效應研究*

李逸候1)楊 平1,2)董 琴1)

(武漢理工大學交通學院1)武漢 430063) (高性能船舶技術教育部重點實驗室2)武漢 430063)

基于疲勞裂紋尖端循環應力-應變場，引入損傷力學概念，提出了非對稱載荷下考慮累計塑性影響的疲勞裂紋擴展預測模型.基于有限元法和Chaboche循環塑性本構模型，動態模擬單個過載峰作用下的裂紋擴展行為.采用Q345標準緊湊拉伸試樣為研究對象，分析不同時刻單峰過載前后裂紋尖端參數變化規律.著重研究了應力比相同且為正值的情況下，不同過載比對疲勞裂紋擴展速率的影響.結果表明，過載比的增加，會得到更大的裂紋擴展遲滯區域以及更小的裂紋擴展速率.并將理論模型預測結果與有限元結果進行對比，結果吻合.

損傷力學；單峰拉伸過載；裂紋擴展速率預測；有限元分析

0 引 言

疲勞是指材料在應力或應變反復作用下，局部位置產生的永久性損傷，并在一定循環次數后形成裂紋或使裂紋進一步擴展直到完全斷裂的現象.在機械、土木和航天等領域，由于工程構件長期受周期性載荷的作用，疲勞所帶來的影響不可忽視.自18世紀30年代起，疲勞問題的各項研究陸續展開，以提高安全性以及使用壽命為主要目的.目前，人們通過對恒幅疲勞載荷下裂紋擴展行為的研究，較好地揭示了裂紋擴展的規律.但在工程實際中，構件往往受到變幅載荷的作用， 常規的Paris公式已無法正確描述其裂紋擴展行為，其裂紋擴展規律仍然是一個尚未解決的難題[1].

變幅載荷下的疲勞裂紋擴展這一課題已經被研究了很長一段時間，Chen等[2]在上世紀初取得了重大突破.為解決變幅載荷下的損傷累積問題，他們提出了線性損傷假設.然而，近幾十年的研究表明，載荷之間還存在很強的交互作用.載荷幅值的變化引起材料疲勞性能的變化，從而加載序列對疲勞壽命也存在一定影響.

近幾十年間，國內外學者在過載裂紋擴展研究方面有了不小的突破.Sander等[3]采用鋁合金，進行了緊湊拉伸試樣的高低載試驗，總結出裂紋擴展遲滯循環數N、應力強度因子幅值 和過載比 之間的影響關系.Silva等[4-5]對低碳鋼CK45、純鋁AL7175和鐵合金Ti6A14V 3種金屬材料進行了拉伸過載后疲勞裂紋擴展試驗，比較了3種材料過載后的裂紋擴展遲滯，研究的大體思路包括：(1)通過過載試驗和有限元模擬，研究過載引起的裂紋擴展行為的作用機理；(2)開展過載作用下的疲勞裂紋擴展試驗，根據不同參數下的實驗結果，總結過載對疲勞裂紋擴展行為的影響機理；(3)建立預測疲勞裂紋擴展速率和疲勞壽命的數學模型.

以往對于變幅載荷作用下的疲勞裂紋擴展行為研究，以定性研究為主，并未展開較為完善的定量分析.文中針對Q345鋼標準緊湊拉伸(compact tension，CT)試樣，對恒幅載荷加載條件下的單峰拉伸過載的疲勞裂紋擴展機理進行研究.基于裂尖應力應變場分析，引入損傷力學概念，提出了非對稱載荷下考慮累計塑性影響的疲勞裂紋擴展速率預測模型.并基于臨界距離理論，考慮到塑性耗散能密度累積過程，運用ABAQUS及MATLAB軟件對Q345鋼的標準CT試樣進行數值仿真，從而預測其疲勞裂紋擴展速率.比較發現理論預測結果與有限元結果相似，并用有限元方法探究了應力比為正且保持不變時，不同過載比對裂紋擴展速率的影響.

1 疲勞裂紋擴展預測模型

1.1 裂紋尖端附近應力應變場描述

試件在單個拉伸過載的循環載荷作用下，裂紋尖端位置處于應力集中狀態，其產生的高應力促使材料發生塑性屈服.裂尖附近塑性區又可分為循環塑性區rc max和單調塑性區rm max，其大小分別為[6]

(1)

由于裂紋尖端處于不同的應力區域，因此其應力場存在彈性、塑性等不同形式.根據Schwable所提出的彈塑性裂尖應力-應變HRR場[7].平面應力狀態下裂紋尖端的線彈性應力場公式為

(2)

(3)

式中：ΔK為應力強度因子幅值；E為彈性模量；μ為泊松比；r為擴展方向上材料點距裂尖的距離；r0為裂尖鈍化半徑.

1.2 低周疲勞臨界損傷

構件在實際復議過程中會承受非對稱載荷的作用，可能會產生塑性的循環累積現象.假設低周疲勞的總損傷為低周疲勞損傷Df和累積塑性損傷Dr之和

D=Df+Dr

(4)

利用線性累積損傷法則，得

(5)

式中：Nf為由低周疲勞控制的失效循環周次；Nr為由累積塑性應變控制的失效循環周次.

1) 采用 Manson-Coffin模型來描述構件單軸低周疲勞行為，得到其壽命關系

(6)

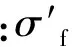
因為塑性區彈性變形分量很小，故可略去彈性項，得到

(7)

2) 采用Xia[8]提出的模型計算由累積塑性應變控制的失效循環周次.

(8)

則

(9)

因此考慮累積塑性影響的疲勞損傷參量為

(10)

1.3 疲勞裂紋擴展預測

(11)

式(11)即為文中裂紋擴展速率預測模型.根據此預測模型，文中將對Q345鋼的標準CT試樣進行低周疲勞裂紋擴展速率預測，并結合有限元仿真結果進行比較.

2 有限元仿真預測

2.1 有限元模型

通過有限元軟件ABAQUS軟件，建立Q345鋼CT標準試樣模型，采用四節點平面應力單元(CPS4)進行網格劃分，見圖1.a取19.5mm，b取6.5mm，W取15.6mm，L取32.5mm.材料參數見表1.

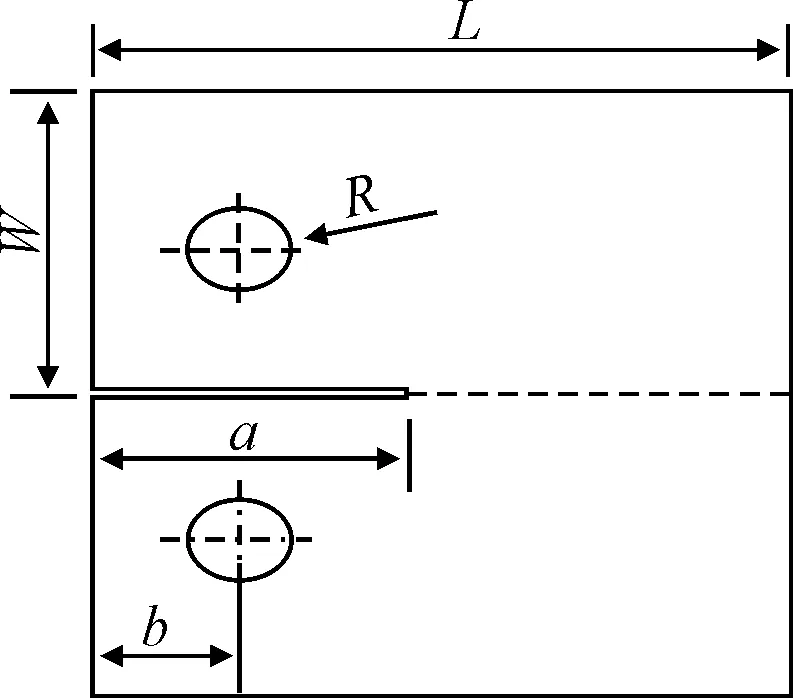
圖1 標準CT試樣

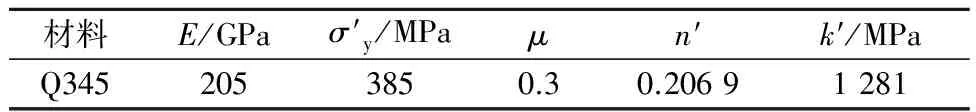
材料E/GPaσ′y/MPaμn′k′/MPaQ3452053850．30．20691281

本構關系采取Chaboche所提出的模型，參數見表2.

表2 Chaboche模型參數

2.2 有限元建模方法

考慮到裂尖附近區域處于應力集中狀態，應力場存在奇異性，其應力-應變梯度變化較大，因此，必須對裂尖附近區域網格進行局部加密處理，見圖2.通過編寫的python小程序對其進行劃分.細化網格尺寸采用文獻推薦的邊長為55 μm的正方形單元.除此之外，在interaction-special中定義裂紋尖端處奇異性，在crack中定義完裂紋面、裂紋尖端以及裂紋擴展速度后，在singularity中選擇midsidenodeparameter中輸入0.25奇異單元來模擬其尖端奇異性，通過將四邊形8節點單元任意2邊的中點向2邊交點移動1/4的距離，得到1/4奇異單元.在裂紋尖端布置此1/4奇異單元.

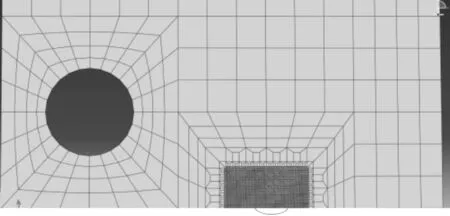
圖2 CT試樣的網格圖

采用定義主從接觸表面的方式來分析裂紋面的接觸問題.將CT試樣分為上下2部分，將上下2部分的對稱軸定義為X軸，將下半部分在X軸上的面定義為主面，上半部分同樣在X軸上面定義為從屬面.計算前，設置主從面上有接觸的所有節點都處于“粘結”(bonded)狀態.在有限元運算過程中，通過對裂尖處主從面粘結幾點的依次“脫粘”(debond)來模擬新裂尖的產生，及裂紋動態擴展過程.

Debond采用ABAQUS自帶的crack length準則，對裂紋長度與加載時間的關系進行人為的規定，從而模擬裂紋擴展的過程以及得到比較準確的應力應變場.其具體操作如下.

在裂紋未起裂時，施加5個恒幅加載循環[9]，再釋放裂尖前端第1個節點的y方向位移約束，裂紋向前擴展1個單元的距離；新的裂尖產生后，系統自動更新接觸對，再同樣施加5個恒幅循環加載，進行下1個節點y方向位移約束的釋放.照此規律完成整個裂紋擴展的過程.每個節點釋放前所加的恒幅載荷作用在于得到裂紋尖端穩定的應力應變場，與裂紋擴展速率無關.

2.3 裂紋尖端的應力場分布

模型載荷采用循環等幅載荷條件下的單峰拉伸過載，見圖3.圖中d點為單峰過載峰值點，其他為循環等幅加載階段.

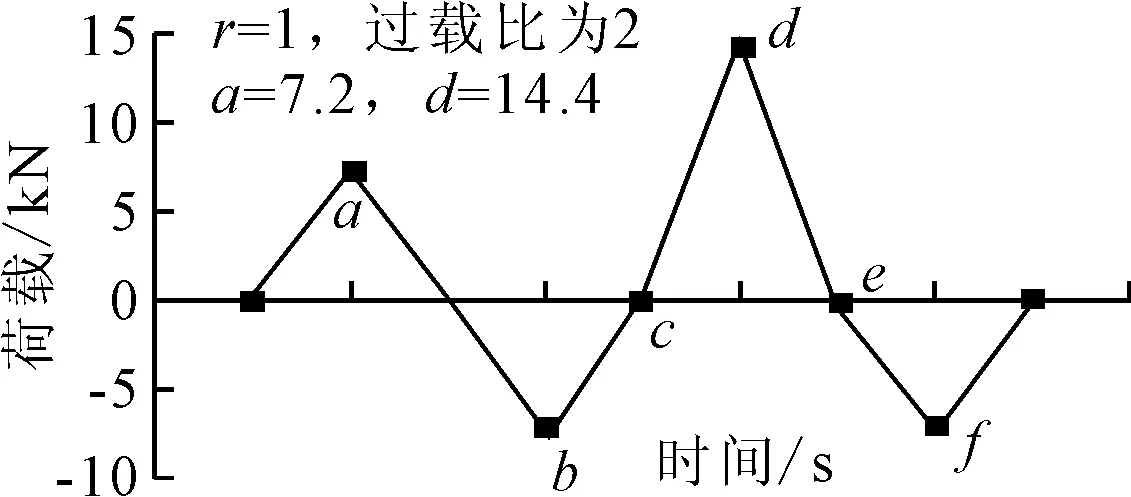
圖3 單峰拉伸過載示意圖

圖4為當節點釋放到過載時刻，在裂紋擴展方向上距新的裂紋尖端r距離的各點的應力分布值，圖中6條曲線的時刻取值參考圖3.由圖4可知，a點為常幅載荷峰值時刻，裂尖出于拉伸屈服狀態；d點為拉伸過載載荷峰值時刻，其應力水平較a處有明顯上升且曲線走勢相似.b和f分別為一般情況下的壓載峰值和經歷過單次拉伸過載的壓載峰值時刻，在裂尖位置，f時刻壓應力略小于b時刻；逐漸遠離裂尖，b點時刻壓應力逐漸減小且在小范圍內轉變為拉應力，而f點時刻壓應力較平穩的減小，其趨勢與外載荷由過載峰值卸載到0時刻的趨勢相近.a和d、b和f2組曲線在裂紋尖端前局部應力分布的明顯差異表明單次的拉伸過載對裂紋尖端前局部應力分布有很大的影響.

圖4 過載節點處應力分布

2.4 裂紋擴展速率

近幾十年來，臨界距離理論被廣泛運用于預測缺口零件的疲勞強度[10].基于臨界距離理論，借助軟件MATLAB軟件對ABAQUS數據進行后處理[11].首先運用有限元軟件ABAQUS模擬裂紋擴展過程，得出每個裂尖節點前方個單元積分點1個循環下的塑性耗散能密度增量[12]，再將這些數據導入MATLAB軟件編制好的后處理程序.此程序主要模擬其塑性耗散能累積過程，并計算出不同時刻裂紋擴展速率.

其核心思想為：裂尖前方一定距離處(結合臨界距離理論)，單元積分點的塑性耗散能密度累積到一臨界值時，當前裂紋尖端單元發生破壞且向前擴展1個單元.瞬時裂紋擴展速率即為單個有限元單元長度除以塑性耗散能密度累積所需的循環數.

根據有限元方法以及理論方法分別繪制Q345鋼標準CT試樣在循環拉伸載荷條件下單個拉伸過載載荷作用下的裂紋擴展速率曲線.其中常幅載荷峰為7.2 kN，應力比R取0.1，見圖5～6.

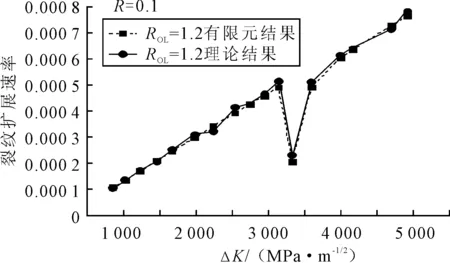
圖5 過載比為1.2疲勞裂紋擴展速率預測結果

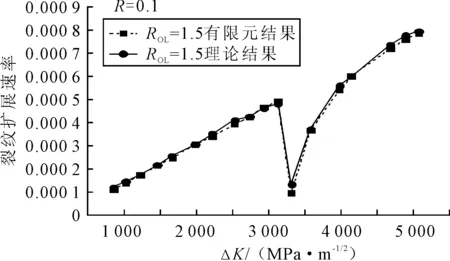
圖6 過載比為1.5時疲勞裂紋擴展速率預測結果

由圖5～6可知，有限元結果與理論結果曲線基本重合，分散性較小，說明文中有限元模型以及理論模型具有一定的可行性.下面利用有限元方法，對相同應力比下，不同過載比的疲勞裂紋擴展速率進行預測，結果見圖7.

圖7 應力比0.1時，單個拉伸過載作用下裂紋擴展速率有限元預測結果

由圖7可知，引入單個拉伸過載后，整個裂紋擴展過程受到了明顯的影響.在施加過載后，裂紋擴展速率出現了快速的減小，在降至最低點后又以較快速度回升到正常水平.整個過程可以劃分為幾個階段：單個拉伸過載前的穩定擴展階段、過載造成的遲滯擴展階段和過載后的穩定擴展階段.通過對圖7的3條曲線的比較可知，更大的過載比會形成更大的遲滯擴展區域和更小的遲滯擴展速率.

3 結 論

1) 對比理論預測結果與有限元預測結果吻合度良好，表明考慮累積塑性影響的低周疲勞裂紋擴展速率預測方法是可行的.

2) 過載對裂紋尖端位置附近局部區域應力場有很大影響，此影響會隨著恒幅載荷的施加逐漸減弱，直至恢復到過載施加之前的應力水平.

3) 當應力比值為正且保持不變時，對同一試件，更大的過載比會形成更明顯的裂紋擴展速率遲滯現象和更小的遲滯擴展速率.

[1]PARIS P C, ERDOGAN F. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering,1963,85(4):528-533.

[2]CHEN N Z, WANG G，SOARES C G. Palmgren-miner’s rule and fracture mechanics-based inspection planning[J]. Engineering Fracture Mechanics,2011,78(18):3166-3182.

[3]SANDER M, RICHARD H A. Lifetime predictions for real loading situations-concepts and experimental results of fatigue crack growth[J]. International Journal of Fatigue,2003,25(9):999-1005.

[4]SILVA F S. Fatigue crack propagation after overloading and underloading at negative stress ratios[J]. International Journal of Fatigue,2007,29(9):1757-1771.

[5]丁振宇.過載作用下疲勞裂紋擴展行為的內在機理研究[D].杭州：浙江工業大學,2013.

[6]CASTRO J T P, MEGGIOLARO M A, MIRANDA A C O. Singular and non-singular approaches for predicting fatigue crack growth behavior[J]. International Journal of Fatigue,2005,27:1366-1388.

[7]SCHWABLE K H. Comparison of several fatigue crack propagation laws with experimental results[J]. Engineering Fracture Mechanics,1974,6(2):325-341.

[8]XIA Z, KUJAWSKI D, ELLYIN F. Effect of mean stress and ratcheting strain on fatigue life of steel[J]. International Journal of Fatigue,1996,18(5):335-341.

[9]ZHENG H, CUI X,SU C C, et al. Numerical modeling of fatigue crack propagation based on the theory of critical distances[J]. Engineering Fracture Mechanics,2013,114:151-165.

[10]TAYLOR D. The theory of critical distances[J]. Engineering Fracture Mechanics,2008,75:1696-1705.

[11]鄭鑫.鑄鋁合金的高低周復合疲勞裂紋擴展和壽命研究[D].南京：南京航天航空大學，2012.

[12]SIH G C, MOYER E T. Path dependent nature of fatigue crack growth[J]. Engineering Fracture Mechanics,1983,17(3):269-280.

Study on Overload Effects of Fatigue Crack Propagation Behavior Based on Accumulative Plastic Damage

LI Yihou1)YANG Ping1,2)DONG Qin1)

(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)1)(KeyLaboratoryofHighPerformanceShipTechnology,MinistryofEducation,Wuhan430063,China)2)

An analytical model for predicting the low cycle fatigue crack propagation rate of plates has been proposed taking into account the accumulative plastic damage by the concept of damage mechanics and cycling stress and strain field at crack tip. The dynamic crack propagation behavior is modeled by the finite element method and Chaboche cyclic plastic constitutive model. The change rule of the crack tip parameter in the different time near the peak of single overloading uses the Q345 steel as experimental subject. The comparison between the theoretical predicted results and the FE results shows good agreement. In this study, the focus is to obtain the effect of overload ratios on fatigue crack propagation rate when the stress ratio stays the same and is positive. The FE results show that the increase of overload ratio induces more significant retardation after single tensile overload.

damage mechanics; single tensile overload; crack growth rate prediction; finite element method

2016-10-24

*國家自然科學基金項目資助(51479153)

U661.41

10.3963/j.issn.2095-3844.2016.06.014

李逸候(1992—)：男，碩士生，主要研究領域為船舶結構