基于復雜約束的多個集裝箱配載優化問題研究

陸 華 趙 琨

(北京物資學院物流學院 北京 101149)

基于復雜約束的多個集裝箱配載優化問題研究

陸 華 趙 琨

(北京物資學院物流學院 北京 101149)

根據集裝箱配載問題中現實存在的多個制約因素，構建了多個集裝箱配載優化模型.為尋求最優解，設計了以預分配策略為原則的遺傳算法和啟發式算法交互進行的混合算法.通過算例驗證和比較得出，該模型算法在滿足集裝箱重心要求、下層貨物額定承重能力，以及貨物混裝限制等約束條件下，可得到較高集裝箱容積利用率的配載方案.

多個集裝箱配載；遺傳算法；啟發式算法；復雜約束

0 引 言

集裝箱配載效率是集裝箱多式聯運運行的一個重要指標，是指將典型形狀的貨物(通常為長方體或立方體，例如，各種紙箱)如何在集裝箱內部擺列實現空間利用優化的問題，也就是探尋如何優化立體貨物在集裝箱內部的擺放布置，實現將所有貨物配載完畢后，所使用的集裝箱數量最少.

配載問題根據需配裝的集裝箱數目的多少可以劃分為單個集裝箱和多個集裝箱配載問題.單箱布局優化方法有啟發式方法、數學規劃、圖論法、遺傳算法、模擬退火法等方法.George 等[1]利用構造型啟發式算法來研究集裝箱配載問題，首次提出“層”的概念.Pisinger[2]也根據“層”的概念提出了一種啟發式算法，將集裝箱內部空間劃分成幾個垂直的列，然后將列分成幾個水平的層，合適的列寬和層深利用分支定界法得到，這種設計的配裝方式可以獲得較高的集裝箱利用率，然而貨物穩定性卻較低，往往上層貨物得不到下層貨物的全面支撐.Loe等[3]對裝載的貨物以“層”的狀態出現，也就是從下至上實現裝箱工作，為了達到平坦的“層”面，該算法根據適箱貨物的高度設立裝載的優先級別.姜義東等[4]采用三叉樹的數據結構來構思集裝箱內部空間布局的優化算法，其將體積大的貨物給予優先級，依次放入集裝箱，這樣處理空間導致產生較為零碎的狹長部分，降低空間利用率，但算法較為簡單減少復雜性.

針對集裝箱多箱配裝問題，Bortfeklt[5]論述了多種形狀貨物組合的連續性配裝設計，但采用該設計常常導致體積大的物品留在最后放置，因而集裝箱內部空間利用率較低.Eley[6]設計了多個集裝箱同時裝載方案，利用單箱裝載方案解決多箱裝載問題，該算法在強異類貨物的裝載問題得到較大改善，得到較高的集裝箱內部空間利用率，在貨物裝載穩定性上不錯.Terno等[7]采用預分配原則，在分支定界概念和啟發式方法的基礎上進行優化，首先采用貪婪算法得到初始解，之后逐步迭代優化.

文中將啟發式算法和預分配原則的遺傳算法相結合，設計一種2種算法交互進行的算法，該算法加入了現實裝載中應考慮的下層貨物承載能力、集裝箱重心配置和不同貨物混裝問題.根據數值測試表明，該算法較好的解決了實際中問題，獲得較好的集裝箱內部空間利用率.

1 集裝箱配載模型及求解算法

1.1 研究對象及約束條件

文中的研究對象是多箱配裝問題，以國際標準集裝箱為配裝箱型，將已經界定的不同種類和不同大小的貨物裝入多個集裝箱，通過算法設計貨物的配載優化布局，使得在滿足多項約束條件的前提下，使用最少的集裝箱數量.

在實際的集裝箱配載中，需要考慮約束條件如下：(1)在實際的裝箱操作中，很多貨物不能倒置，本算法要求貨物不能倒置；(2)單件貨物的體積不能超過集裝箱的界限限制；(3)裝入貨物的總重量小于或等于集裝箱的額定載重量；(4)貨物裝載必須有足夠的支撐，不能懸空，必須放在其他貨物的上方；(5)為了確保裝卸過程的穩定性，要求配裝完畢后的集裝箱重心在合理的范圍內；(6)考慮不同貨物不能混裝的問題，本算法設計了配裝隔離約束，也就是限制貨物的混裝，例如，不同化學用品不能混裝；(7)每件貨物都有一定的承重能力，因此，需要考慮貨物承重能力的約束，也就是上層貨物的總質量不能超過下層貨物的承重能力.

1.2 假設條件

由于實際問題非常復雜，為了避免不必要的復雜性，文中做出以下假設：(1)所裝貨物都是長方體或立方體；(2)貨物的重心和其他幾個中心一致；(3)貨物中途不會出現掏箱問題；(4)貨物裝載過程中不會出現變形.

2 構建模型

2.1 符號說明

將貨物和集裝箱放置于笛卡爾三維坐標系中，坐標系中X軸正向方向為集裝箱的長度方向，Y軸正向方向為集裝箱的寬度方向，Z軸正向方向為集裝箱的高度方向，集裝箱左后角位于坐標系的原點上(0,0,0)見圖1.

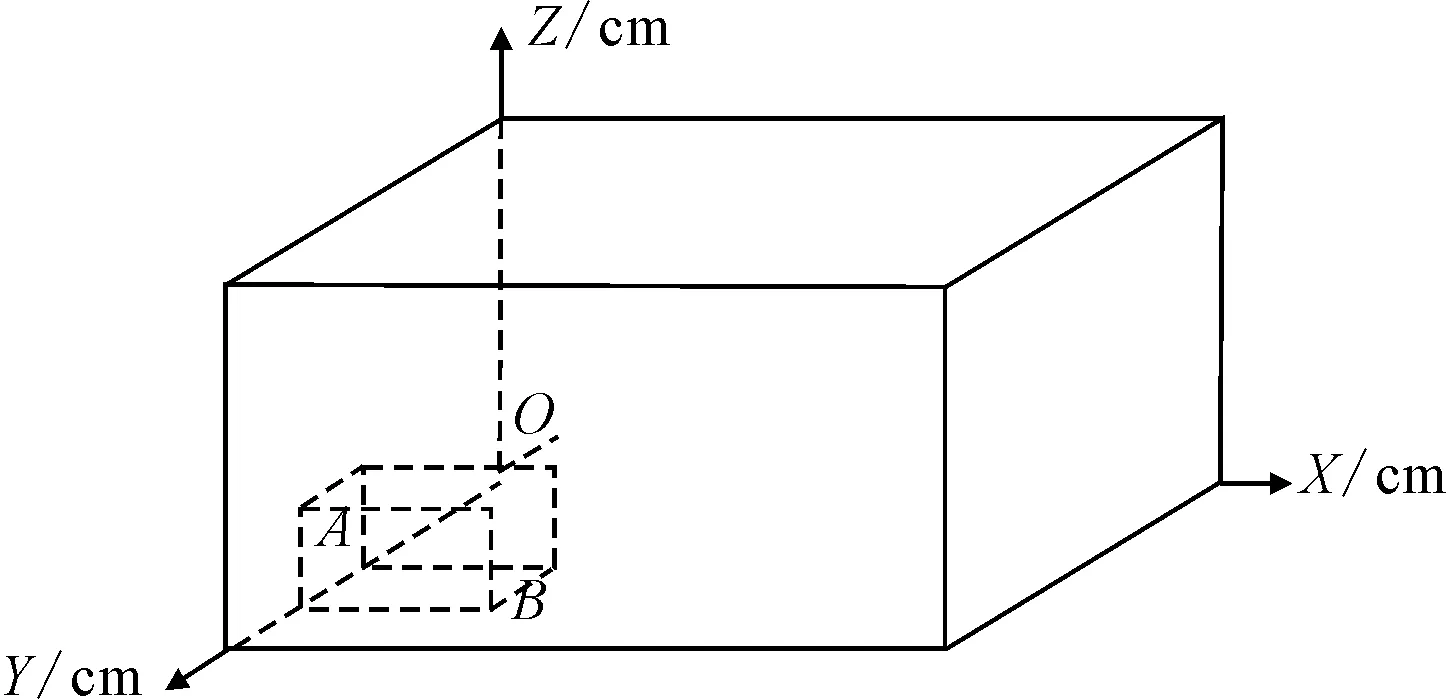
圖1 集裝箱坐標示意圖

2.2 目標函數與現實約束條件

優化目標為最小化集裝箱的使用數量，則目標函數可以表示為

(1)

約束條件：

?i=1,2,…,n

(2)

(3)

式中：

spj=[(xbj-xaj+xbp-xap)-

(max{xbp,xaj}-min{xap,xaj})]×

[(ybj-yaj+ybp-yap)-(max{ybp,ybj}-

min{yap,yaj})]

(4)

xlp≤xlj,xbp≥xbj,yap≤yaj,

max{xbp,xbj}-min{xap,xaj}<

xbj-xaj+xbp-xap,

max{ybp,ybj}-min{yap,ybj}<

ybj-yaj+ybp-yap}

(5)

i=1,2,…,N}

(6)

[(xbj-xaj)-lj][(ybj-yaj)-wj]=0,

?j∈{Xij=1,i=1,2,…,N}

(7)

minxaj≥0;minyaj≥0;minzaj≥0,

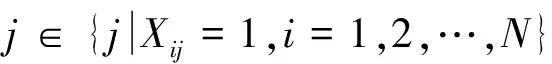
(8)

maxxbj≥0;maxybj≥0;maxzbj≥0,

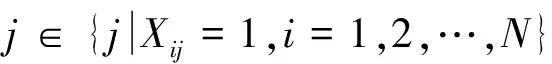
(9)

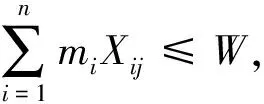
(10)

XjkXik(1-rij)=0,

?k∈1,2,…,N;?j∈1,2,…,n

(11)

?i∈1,2,…,N

(12)

?i∈1,2,…,N

(13)

?i∈1,2,…,N

(14)

?j=1,2,…,n

(15)

式中：

yai≥ya2,xbi≤xbj,ybi≤ybj}

(16)

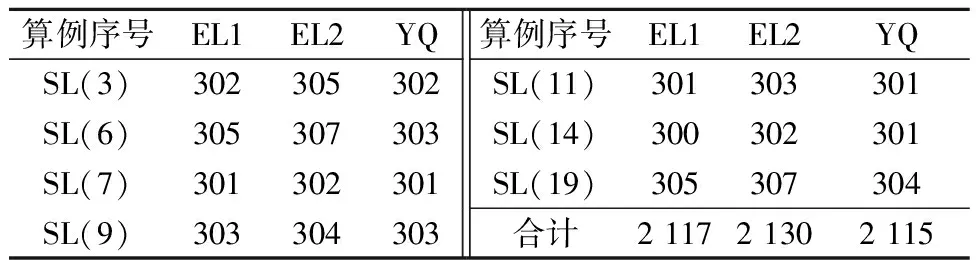
min{xaq,xaj}

max{ybq,ybj}-min{yaq,yaj}

ybq-yaq},?k∈1,2,…,N

(17)

上述模型中，式(2)為貨物都務必全部裝入到集裝箱；式(4)為箱內上下兩層相鄰貨物之間的重合面積；式(5)為箱內上下兩層相鄰貨物重合情況由完全重合和部分重合組成；式(3)～(5)組合為貨物必須完全放在下一層貨物的上面，不存在懸空放置的情況；式(6)為所有貨物不能上下顛倒放置；式(7)為貨物的放置與集裝箱內部長度或寬度方向垂直或平行；式(8)～(9)為全部貨物的體積小于或等于集裝箱內部容積界限；式(10)為箱內貨物總重小于或等于集裝箱額定載重量；式(11)為不能混裝的貨物不能裝載在一起，需要滿足貨物隔離限制；式(12)～(14)為裝載完畢后集裝箱的重心位置應在要求范圍內；式(15)為集裝箱內上下兩層相鄰貨物的由完全重合和部分重合兩種形式構成；式(16)～(17)為上下貨物中，上層所有貨物總重不能超過下層貨物所能承受的最大重量.

3 混合算法設計

由于該問題實際約束較為復雜，文中結合采用遺傳算法預啟發式算法相結合交互式的混合算法.首先，利用遺傳算法具有全局搜索能力做出集裝箱配載的預分配，再使用啟發式算法進行迭代，產生不同的集裝箱配載方案，2個算法交替進行優化.算法設計流程見圖2.

圖2 遺傳算法預啟發式算法的交互設計流程圖

該算法結合了遺傳算法和啟發式算法的優點，算法效率較高，可以實現較高的集裝箱內部空間利用率，同時還考慮在裝卸過程中集裝箱的重心要求、避免貨物承受過重載荷造成貨損以及不同貨物不能混載的要求.算法主要參數取值如下：遺傳算法群體規模數為50，最大迭代代數為350，變異操作次數取100，交叉概率為0.95，變異概率為0.01.

4 算法評價

4.1 與現行研究的比較

為了對設計的遺傳和啟發式結合的混合式算法進行檢驗，文中采用OR-LIBRARY的基準測試問題來評判[8].標準算例借鑒Bischoff等[9-10]所采用的算例，共7大類，每一類有50個算例.所用集裝箱為20 ft國際標準集裝箱，尺寸為5.898 m×2.352 m×2.385 m.文中采用目前取得較好效果的Elay的2種算法，用EL1和EL2表示，文中設計算法用YQ表示.

現有的研究資料表明，目前對于集裝箱內裝載優化問題主要考慮集裝箱內容積限制，對于集裝箱內部貨物承重限額、集裝箱吊裝重心要求缺乏考慮.文中設計的優化模型的優點在于，不僅考慮貨物的體積，還考慮貨物在集裝箱內的承重限額、貨物混載限制及重心穩性要求等約束條件.

關于啟發式-變異算法的參數比較結果見表1～2.

表1 交互式混合算法與目前應用算法的結果比較(所需集裝箱個數)

算例序號EL1EL2YQSL(3)302305302SL(6)305307303SL(7)301302301SL(9)303304303算例序號EL1EL2YQSL(11)301303301SL(14)300302301SL(19)305307304合計211721302115

注釋：括號()內的數字是該算例中貨物的種類數目

由表1的7個算例可知，文中算法YQ和算法EL2相比，使用集裝箱數量較少，YQ與算法EL1相比，不多于EL1所使用的集裝箱數量.由表2可知，YQ的前5個集裝箱容積平均利用率比EL1更加平均，并且對7個算例總體來看，YQ的集裝箱內部容積利用率的平均值均大于算法EL1，表明文中設計算法在充分利用集裝箱內部容積上取得較好的效果.

表2 文中設計算法(YQ)與算法EL1的集裝箱配載容積利用率比較

4.2 2種分配原則的比較

由于根據目前研究資料缺乏對貨物承載限額、貨物混裝限制及集裝箱重心位置要求的研究，因此無法做出這方面的比較.目前較為常用的連續性分配策略，而文中采用遺傳算法進行貨物裝載的預分配策略，因此，對不同分配策略進行比較，結果見表3.由表3可知，預分配策略的集裝箱內容容積利用率(91.60%)略高于連續性策略取得結果(91.00%).主要原因在于，采用遺傳算法進行預分配，而遺傳算法具有全局搜索優化能力；其次是啟發式算法與遺傳式算法的交互進行，也就是將單個集裝箱配載的結果與多個集裝箱配載的結果進行再次平衡優化.

表3 連續分配原則與預分配原則的集裝箱利用率 %

5 結 束 語

研究了在實際復雜的約束限制下，多個集裝箱內部配載優化問題，對集裝箱重心要求、下層貨物承重能力、不同貨物混載限制等多個實際因素進行考慮，構建了多個集裝箱配載的混合整數規劃模型，在模型算法上設計了預分配原則，將遺傳算法和啟發式算法相結合進行交互式計算的混合算法.通過算例測試，與目前流行算法相比，文中算法取得了較好的集裝箱配載效果，使的集裝箱容積平均利用率較高，使用集裝箱數量較少.不足之處，在于沒有考慮其他典型形狀的貨物，例如卷盤狀，桶裝貨物和托盤等貨物，以及中途掏箱的情況也未考慮.

[1]GEORGE J A, ROBINSON D F. A heuristic for packing boxes into a container[J]. Computer and Operational Research,1980(7):147-156.

[2]PISINGER D. Heuristics for the container loading problem[J]. European Journal of Operational Research,2002,141:382-92.

[3]lOE T H, NEE A Y C. A packing algorithm for hexahedral boxes[C]. Proceeding of the Conference of Industrial Automation, Singapore,1992:115-126.

[4]姜義東，查建中，何大勇.集裝箱裝載矩形貨物的布局研究[J].鐵道學報，2000,22(6):13-18.

[5]BORTFELDT A. Heuristik fuer multiple container lade probleme[J]. Or Spektrum,2000,22(2):239-262.

[6]ELEY M. Solving container loading problems by block arrangement[J]. European Journal of Operational Research,2002,141:393-409.

[7]TERNO J, SCHEITHAUER G, SOMMERWEIU U, et al. An efficient approach for the multi-pallet loading problem[J]. European Journal of Operational Research,2000,123:372-381

[8]BEASLEY J E. OR-library: distributing test problems by electronic mail[J]. Journal of Operation Research Society,1990,41(11):1069-1072.

[9]BISCHOFF E E, RATCLI M S W. Issues in the development of approaches to container loading[J]. Omega,1995,23(4):377-390.

[10]JIN Z H, ITO T, OHNO K. The threo-dimensional bin packing problem and its practical algorithm[J]. International Journal of Japan Society of Mechanical Engineers,2003,46(1):60-66.

Optimization of the Multi-containers Loading Problems Based on Complex Constraints

LU Hua ZHAO Kun

(LogisticsSchool,BeijingWuziUniversity,Beijing101149,China)

According to the multiple constraints existing in the actual container loading problem, the paper establishes multiple containers loading optimization of mixed integer programming model. In order to obtain the optimal solution, the paper designs a hybrid algorithm based on genetic algorithm and heuristic algorithm, which is based on the principle of pre-allocation strategy. Through the example verification and comparison, the model algorithm satisfies the constraints, the focus of container goods and mixed goods bearing capacity constraints, can obtain higher utilization ratio of the volume of container stowage solution.

multiple containers loading; genetic algorithm; heuristic algorithm; complex constraints

2016-11-03

U169

10.3963/j.issn.2095-3844.2016.06.023

陸華(1977—):女，博士，主要研究領域為運輸與物流