基于單軸壓縮蠕變試驗求解瀝青混合料松弛模量*

呂慧杰 劉涵奇 羅 蓉

(武漢理工大學交通學院 武漢 430063)

基于單軸壓縮蠕變試驗求解瀝青混合料松弛模量*

呂慧杰 劉涵奇 羅 蓉

(武漢理工大學交通學院 武漢 430063)

為了更加精確、方便地獲得瀝青混合料的松弛模量，對處于線性粘彈性狀態的瀝青混合料試件進行單軸壓縮蠕變試驗，根據蠕變柔量和松弛模量在拉普拉斯域內的轉換關系，通過測得的蠕變柔量計算得到瀝青混合料的松弛模量.結果表明，瀝青混合料蠕變柔量和松弛模量的相互轉換建立在線性粘彈性基礎上，實現蠕變柔量向松弛模量的轉化本質上是實現廣義開爾文模型向廣義麥克斯韋爾模型的轉化.所提出的方法可用于以松弛模量為基礎的瀝青混合料粘彈性本構模型中，用于預測瀝青路面的粘彈性響應.

道路工程；瀝青混合料；蠕變柔量；松弛模量；線性粘彈性

0 引 言

瀝青混合料是一種復雜的粘彈性材料，其線性粘彈性質是后續研究瀝青路面開裂和永久變形的基礎[1-3].松弛模量是研究瀝青混合料線性粘彈性能的重要參數之一，理論上可以通過應力松弛試驗直接測定松弛模量.應力松弛試驗是在試驗開始的很短時間內輸入一個恒定的應變，目前的試驗儀器很難實現，試驗造成的誤差較大，操作具有一定的難度[4].文獻[5-7]通過復數模量試驗間接確定了松弛模量.然而，在測定復數模量時，需要在幾個不同的溫度下進行若干頻率的試驗，試驗過程較復雜，耗時長.

松弛模量和蠕變柔量是瀝青混合料粘彈性性質的2種表現形式，兩者之間存在相互轉換的關系.因此，瀝青混合料的松弛模量可先通過較為簡單的蠕變試驗測得蠕變柔量，然后再經由蠕變柔量轉換求得.該方法已被黃文柯等[8]證實，但在進行蠕變試驗時并未考慮松弛模量和蠕變柔量相互轉換的必要條件，即瀝青混合料必須處于線性粘彈性狀態，只是進行了不同應力水平下的蠕變試驗.

文中基于線性粘彈性力學理論，采用廣義開爾文模型和廣義麥克斯韋爾模型對瀝青混合料的蠕變柔量和松弛模量分別進行表征，根據蠕變柔量和松弛模量在拉普拉斯域內的轉換關系，通過對線性粘彈性狀態下的瀝青混合料試件進行蠕變試驗，以期通過蠕變柔量求得瀝青混合料的松弛模量.瀝青混合料試件處于線性粘彈性狀態將通過3種小應力水平下的蠕變試驗試驗結果和1種小應力水平下的復數模量試驗試驗結果共同驗證.

1 蠕變柔量與松弛模量性質

1.1 蠕變柔量與松弛模量及其Prony表達式

瀝青混合料的蠕變柔量和松弛模量通常采用彈簧和粘壺組成的力學模型來表征，其中彈簧用于表征瀝青混合料中的彈性效應，粘壺用于表征瀝青混合料中的粘性效應.目前廣泛采用廣義開爾文模型模擬粘彈性材料的蠕變現象，采用廣義麥克斯韋爾模型模擬粘彈性材料的應力松弛現象[9-11]，見圖1～2.

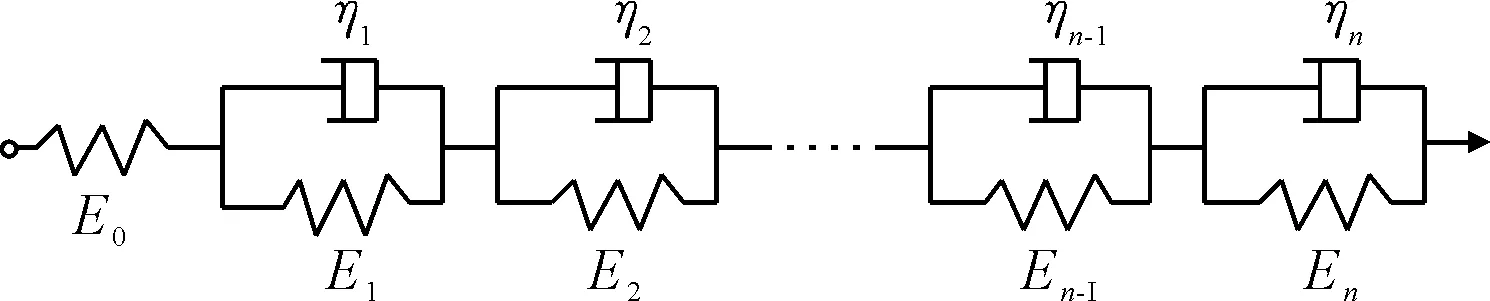
圖1 廣義開爾文模型

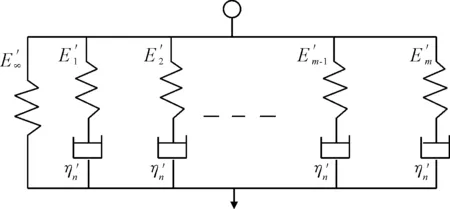
圖2 廣義麥克斯韋爾模型

采用Prony級數的形式對廣義開爾文模型和廣義麥克斯韋爾模型分別進行表征，可得到

(1)

式中：E0為瞬時彈性模量；Ei為第i個開爾文元件中彈簧的彈性模量；ηi為第i個開爾文元件中粘壺的粘度；n為開爾文元件的個數.

(2)

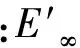
實現蠕變柔量向松弛模量的轉化實際上就是實現廣義開爾文模型向廣義麥克斯韋爾模型的轉化.

1.2 蠕變柔量與松弛模量相互轉換

當瀝青混合料處于線性粘彈性狀態時，其應力應變本構關系可由玻爾茲曼疊加原理進行描述.

1) 在應力控制試驗中，若輸入應力σ(t)，輸出應變ε(t)可以表示為

(3)

式中：τ為虛擬變量，τ∈[0,t]，s；D(t)為當瀝青混合料處于線性粘彈性狀態時的蠕變柔量，MPa-1；σ(t)為輸入應力，Pa；ε(t)為輸出應變.

2) 在應變控制試驗中，若輸入應變ε(t)，輸出應力σ(t)可以表示為

(4)

式中：τ為虛擬變量，τ∈[0,t]，s；E(t)為當瀝青混合料處于線性粘彈性狀態時的松弛模量，MPa；ε(t)為輸入應變；σ(t)為輸出應力，Pa.

根據彈性-粘彈性對應原理，對式(3)和式(4)分別進行拉普拉斯變換，可將時間域內的粘彈性問題轉化為拉普拉斯域內的彈性問題.拉普拉斯變換的定義如下[12].

(5)

根據式(5)對式(3)和式(4)分別進行拉普拉斯變換后可得

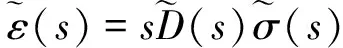
(6)

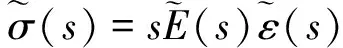
(7)

對式(6)和式(7)進一步分析可得

(8)

式(8)闡明了蠕變柔量和松弛模量在拉普拉斯域內的轉換關系，為通過蠕變柔量(松弛模量)求解松弛模量(蠕變柔量)奠定了理論基礎：

1) 若已知蠕變柔量，可通過式(9)求解松弛模量.

(9)

2) 若已知松弛模量，可通過式(10)求解蠕變柔量.

(10)

式中：L-1{ }為拉普拉斯逆變換算子形式.

文中將利用式(9)實現由蠕變柔量到松弛模量的轉換.

2 單軸壓縮蠕變試驗

2.1 試件制備

文中中蠕變試驗為單軸壓縮蠕變試驗.試驗選用AC-20C石灰巖瀝青混合料，其中瀝青采用SBS改性瀝青，集料采用石灰巖.集料的合成級配見表1，最佳油石比確定為4.30%.

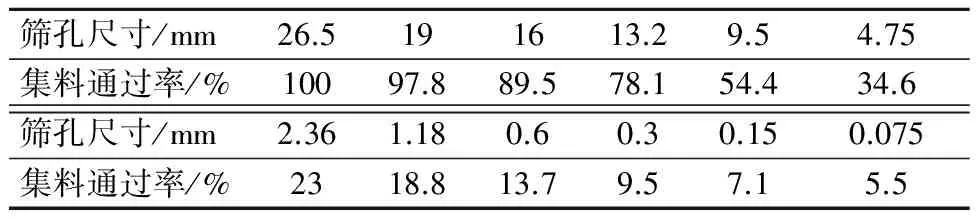
表1 瀝青混合料礦料級配組成

熱拌瀝青混合料(簡稱HMA)試件的制備采用Superpave旋轉壓實的方法，具體操作步驟如下.

步驟1 利用自動拌和儀將加熱后的集料和瀝青在170 ℃下進行拌和，拌和結束后將瀝青混合料散料放置150 ℃的烘箱中進行溫度養生2 h，用于模擬運輸過程中的老化現象.

步驟2 溫度養生結束后，利用旋轉壓實儀成型高度為170 mm、直徑為150 mm的圓柱形試件.

步驟3 待試件完全冷卻后，利用鉆芯機對步驟2所得的試件進行鉆芯，得到高度為170 mm、直徑為100 mm的試件.

步驟4 鉆芯結束后，利用切割鋸對步驟3所得試件的上下兩面各切除10 mm，得到高度為150 mm、直徑為100 mm的試件.

步驟5 試件制備完成后，采用水中重法測量試件的空隙率，試件的空隙率需滿足4.0%±0.5%才能用于蠕變試驗.

本次蠕變試驗采用材料試驗機(簡稱MTS)對2個AC-20C石灰巖HMA試件(分別記作HMA-1和HMA-2分別進行.在開始試驗前，沿著HMA試件側面安裝3個標距為90 mm、相隔120°的位移傳感器用于記錄HMA試件在側面3個位置的軸向方向變形，并取3個位置的軸向方向變形的平均值作為HMA試件在試驗條件下的變形值.

2.2 試驗方案

文中旨在利用蠕變柔量和松弛模量在拉普拉斯域內的轉換關系，見式(9).通過蠕變試驗求解瀝青混合料的松弛模量.式(9)的推導建立在波爾茨曼疊加原理的基礎上，因此式(9)的適用范圍是在進行蠕變試驗時瀝青混合料處于線性粘彈性狀態.當瀝青混合料處于線性粘彈性狀態時，其時間域內的應力應變關系滿足線性疊加原理，用數學方程表示如下.

ε[cσ(t)]=cε[σ(t)]

(11)

ε[σ1(t)+σ2(t-t1)]=

ε[σ1(t)]+ε[σ2(t-t1)]

(12)

式中：c為常數.

當對瀝青混合料進行蠕變試驗時，式(11)和(12)的成立均建立在蠕變柔量隨應力水平的改變保持不變的基礎上；當對瀝青混合料進行復數模量試驗時，式(11)和(12)的成立均建立在動態模量和相位角隨加載周期和應力水平保持不變的基礎上[13-14].因此，為了保證試驗用HMA試件在進行蠕變試驗時處于線性粘彈性狀態，先對該試件進行3種不同小應力水平下的蠕變試驗，比較3次試驗得出的蠕變柔量是否非常接近；在蠕變試驗結束后，再對該試件進行小應力水平下的復數模量試驗，觀察動態模量和相位角隨加載周期的變化是否保持不變，進一步確認試件沒有受到損傷.

本次單軸壓縮蠕變試驗在20 ℃下進行，在正式開始試驗前，試件需要在該溫度下進行至少3 h的溫度養生,以使試件的內部達到溫度平衡.每個試件均進行3種應力水平的蠕變試驗，相鄰2次試驗間隔1 h以使試件的變形完全恢復.在完成3個應力水平下的蠕變試驗、試件休息1 h后，再對同一試件進行復數模量試驗，其中復數模量的加載形式為半正弦波.蠕變試驗和復數模量試驗的試驗方案見表2.

表2 蠕變試驗和復數模量試驗試驗方案

在所有試驗結束后，可以從MTS軟件中讀取軸向力和軸向位移數據用于試驗結果分析.

2.3 試驗結果分析

在從MTS軟件中讀取軸向力和軸向位移的數據后，HMA試件受到的軸向應力和軸向應變分別按照式(13)和(14)求得.

(13)

(14)

式中：σ(t)為試件受到的軸向應力， Pa；F(t)為施加的軸向力， N；r為試件的半徑，即0.05 m；ε(t)為試件產生的軸向應變；Δl為試件的軸向變形量，m；l為試件的標距，即0.09 m.

在求出蠕變試驗中HMA試件所承受的軸向應力和軸向應變后，可計算出蠕變柔量.以HMA-1試件為例，圖3為HMA-1試件在20 ℃ 3種應力水平下測得的蠕變柔量，3種應力水平下的蠕變柔量非常接近說明試件在進行蠕變試驗時處于線性粘彈性階段.

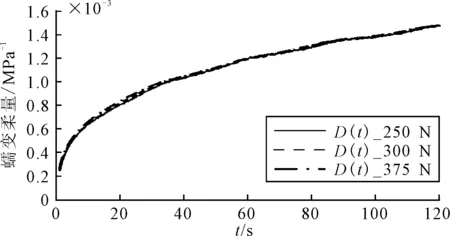
圖3 HMA-1試件3種應力水平下蠕變柔量

復數模量試驗需對HMA試件施加半正弦波荷載.在求出復數模量試驗中HMA試件所承受的軸向應力和軸向應變后，動態模量和相位角可由式(1)求出.

(15)

φ=ωΔt

(16)

式中：σ0為HMA試件承受半正弦荷載的振幅，Pa；ε0為HMA試件產生軸向應變的振幅；ω為復數模量試驗的角頻率，rad/s；Δt為軸向應變與軸向應力的時間差，s.

以HMA-1試件為例，圖4為HMA-1試件在20 ℃復數模量試驗的測得結果，由圖5可知，穩定狀態下的動態模量和相位角隨著加載周期保持不變，進一步說明試件沒有受到損傷.

3種應力水平下蠕變試驗的試驗結果以及復數模量試驗的試驗結果均表明試驗用HMA試件在進行蠕變試驗時處于線性粘彈性狀態，沒有受到損傷.因此可以根據式(9)求解松弛模量.

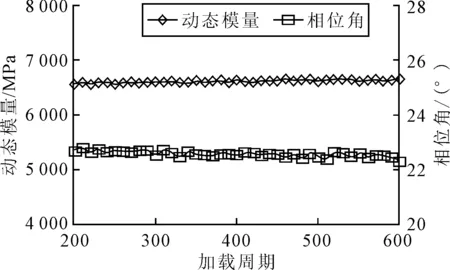
圖4 HMA-1試件動態模量和相位角測量結果

3 由蠕變柔量求解松弛模量

3.1 廣義開爾文模型表征蠕變柔量測量結果

本次蠕變試驗的加載時長為120 s，由于加載時長較短，在利用Prony形式的廣義開爾文模型對蠕變柔量試驗結果(取3種應力水平下蠕變柔量的平均值)進行擬合時，取i=2并將E0，E1，E2，η1，η2均看作擬合參數.在利用Microsoft Excel中的規劃求解功能對模型進行擬合后，得到的擬合結果見圖5，擬合參數見表3.

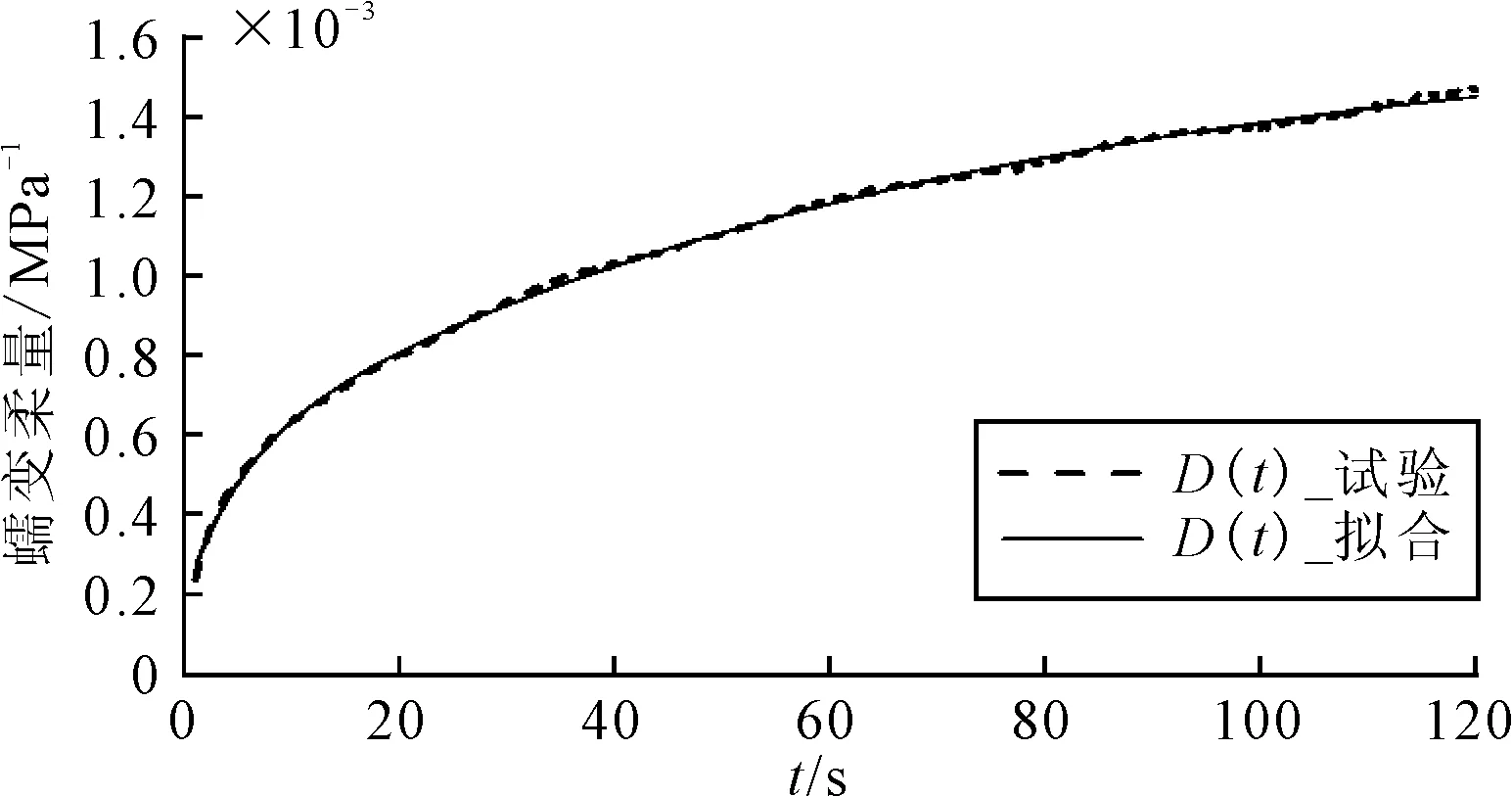
圖5 HMA-1試件蠕變柔量擬合曲線

參數E0E1E2η1η2擬合值4．0322．6460．88320．4080．987

由圖5可知，廣義開爾文模型能夠很好地擬合蠕變柔量測量值，判定系數R2計算為0.998 8.

3.2 基于解析解求解松弛模量

為了通過廣義開爾文模型表征的蠕變柔量求解出松弛模量，先對式(1)進行拉普拉斯變換，可得

(17)

然后將式(17)代入式(9)中求得拉普拉斯域內的松弛模量，即

(18)

為了求解松弛模量的解析解，先對式(18)運用部分分式展開法，即將式(18)看作是2個高階多項式的比值，則有

(19)

式中：a和b均為高階多項式的系數，可通過比較式(18)和式(19)的系數求得.

然后對式(19)的分母進行因式分解，式(19)必定寫成如下形式

(20)

式中：ri為滿足方程B(s)=0中除0以外的根；C0和Ci通過比較式(19)和式(20)的系數求得.

對式(20)應用拉普拉斯逆變換可求得

(21)

顯然，式(21)符合如式(2)所示的廣義麥克斯韋爾模型的Prony形式.對比式(21)和式(2)可知，由廣義開爾文模型表征的蠕變柔量經式(9)推導出的松弛模量恒符合廣義麥克斯韋爾模型的形式.

當i取2時，則有應力松弛模量為

E(t)=C0+C1e-r1t+C2e-r2t

(22)

按照式(18)～(21)所述的因式分解方法，可求得各擬合參數的值.

(23)

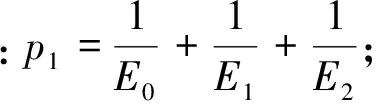
(24)

將3.1求解的廣義開爾文模型各參數值代入式(23)～(24)中即可求解出松弛模量.

3.3 基于數值解求解松弛模量

上述通過松弛模量解析解求解松弛模量的方法具有明確的物理意義，將廣義開爾文模型和廣義麥克斯韋爾模型聯系起來，但是采用因式分解求解松弛模量的解析解比較復雜，更簡便的方法是采用直接求解松弛模量數值解的方法，具體步驟如下:

步驟1 采用廣義開爾文模型對蠕變柔量試驗數據進行擬合，得到模型的各擬合參數.

步驟2 利用MATLAB對拉普拉斯域內的松弛模量(如式(18)所示)進行拉普拉斯逆變換，求解時間域內松弛模量的表達式.

步驟3 將求解的廣義開爾文模型的各擬合參數代入步驟2求得的時間域內松弛模量的表達式，得到松弛模量數據.

步驟4 采用廣義麥克斯韋爾模型對步驟3得到的松弛模量數據進行擬合，由4.2知，判定系數一定為1.

計算結果表明兩種求解方法得到的松弛模量完全相等，見圖6.

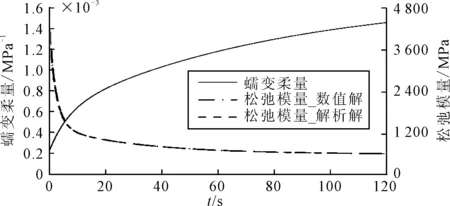
圖6 HMA-1試件蠕變柔量、松弛模量曲線

4 結 論

1) 蠕變柔量和松弛模量的相互轉化建立在線性粘彈性的基礎上.

2) 廣義開爾文模型和廣義麥克斯韋爾模型能夠準確表征瀝青混合料的蠕變和松弛行為，實現蠕變柔量向松弛模量的轉化就是實現廣義開爾文模型向廣義麥克斯韋爾模型的轉化.

3) 可以采用2種方法通過蠕變柔量求解松弛模量，即解析解求解和數值解求解，且2種方法得到的結果完全一致.

[1]SCHAPERY R A. Correspondence principles and a generalized integral for large deformation and fracture analysis of viscoelastic media [J]. International Journal of Fracture,1984,25(3):195-223.

[2]趙延慶,黃大喜,潘有強.利用虛應變分析瀝青混合料的粘彈性質[J].重慶交通大學學報(自然科學版),2008(2):236-239.

[3]ZHANG Y, LUO R, LYTTON R L. Characterizing permanent deformation and fracture of asphalt mixtures by using compressive dynamic modulus tests [J]. Journal of Materials in Civil Engineering, 2012,24(7):898-906.

[4]薛忠軍,張肖寧,詹小麗,等.基于蠕變試驗計算瀝青的低溫松弛彈性模量[J].華南理工大學學報(自然科學版),2007,35(2):64-68.

[5]劉孝敏,唐志平,李欣增.復柔量-蠕變柔量和復模量-松弛模量轉換公式的討論[J].中國科學技術大學學報,1989(4):476-485.

[6]YAN H, ZHANG X, ZHANG L. Methods of fitting the prony series of viscoelastic models of asphalt mixture based on dynamic modulus[C]. International Conference on Transportation Engineering,2015(12):1384-1389.

[7]趙延慶,唐積民,白龍.利用瀝青混合料復數模量確定松弛模量研究[J].建筑材料學報,2012,15(4):498-502.

[8]黃文柯,張麗娟,張肖寧,等.瀝青混合料蠕變柔量轉換為松弛模量的研究[J].交通科學與工程,2015,31(3):7-12.

[9]FINDLEY W N, LAI J S, ONARAN K. Creep and relaxation of nonlinear viscoelastic materials with an introduction to linear viscoelasticity [M]. New York: Dover Publication, 1989.

[10]PARK S W, KIM Y R. Fitting prony-series viscoelastic models with power-law presmoothing [J]. Journal of Materials in Civil Engineering, 2001,13(1):26-32.

[11]SUN Y, CHEN J, HUANG B. Characterization of asphalt concrete linear viscoelastic behavior utilizing havriliak-negami complex modulus model[J]. Construction and Building Materials, 2015(2):226-234.

[12]申建中,劉峰.數學物理方程[M].西安：西安交通大學出版社,2010.

[13]LUO R, LYTTON R L. Characterization of the tensile viscoelastic properties of an undamaged asphalt mixture[J]. Journal of Transportation Engineering, 2010(3):173-180.

[14]LUO X, LUO R, L. LYTTON R L. Characterization of fatigue damage in asphalt mixtures using pseudostrain energy [J]. Journal of Materials in Civil Engineering, 2012,25(2):208-218.

Determination of Relaxation Modulus of Asphalt Mixtures Using Uniaxial Compressive Creep Test

LYU Huijie LIU Hanqi LUO Rong

(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)

In order to obtain the relaxation modulus conveniently and accurately, a material testing system (MTS) is employed to perform uniaxial compressive creep test on asphalt mixture specimens within the linear viscoelastic range. The measured creep compliance is converted into relaxation modulus in accordance with the interrelationship between creep compliance and relaxation modulus in the Laplace domain. Conclusions can be drawn that the interconversion between the creep compliance and relaxation modulus is based on the linear viscoelasticity and converting the creep compliance into relaxation modulus is essentially converting the Generalized Kelvin model into the Generalized Maxwell model. The conversion method proposed in this study can be extensively applied to various viscoelastic constitutive models that are based on the relaxation modulus so as to predict the viscoelastic responses of asphalt pavements.

road engineering; asphalt mixture; creep compliance; relaxation modulus; linear viscoelasticity

2016-10-18

*國家重點基礎研究發展計劃項目資助(2015CB060100)

U416.217

10.3963/j.issn.2095-3844.2016.06.025

呂慧杰(1992—)：男，碩士生，主要研究領域為瀝青路面材料