基于分階段非線性融合的粒子濾波預測算法

張馬蘭

(中航飛機股份有限公司研發中心 西安 710089)

基于分階段非線性融合的粒子濾波預測算法

張馬蘭

(中航飛機股份有限公司研發中心 西安 710089)

針對航空發動機剩余壽命預測問題，采用多參數分階段非線性的融合方法計算了發動機性能指標，結合粒子濾波思想建立了發動機性能衰退模型，借助粒子濾波預測估計了模型的時變參數，有效預測了發動機的剩余壽命，有利于航空發動機剩余壽命預測方法的研究.

航空發動機；融合；粒子濾波；剩余壽命預測

0 引 言

航空發動機是飛機的“心臟”，直接決定了民航運輸的安全及效益.綜合考慮新一代航空運輸系統面臨的“安全關口前移”與“運營成本控制”的雙重標準，以及發動機不能進行周期長且成本高的反復試驗的條件限制.準確地對航空發動機的剩余壽命(residual life，RUL)進行預測成為保證民航安全與效益中亟待解決的問題.

目前，發動機剩余壽命預測多采用基于融合的預測方法，但是缺乏對發動機性能衰退的階段性特點的考慮；另外，Kalman濾波預測算法在發動機剩余壽命預測中應用較為普遍，但其較擅長解決線性和弱非線性問題，而發動機是極其復雜的系統，是強非線性問題.因此，考慮發動機性能衰退分階段的特點及表征參數與性能的非線性映射關系描述其性能衰退趨勢，并采用非線性的預測方法對性能衰退趨勢進行預測極為重要.

1 發動機性能衰退

航空發動機的健康狀況無法直接觀測，但隨著運行時間的增加，其性能衰退會反映在監測參數的變化上.這些參數包括氣路性能參數、滑油參數和振動參數.氣路性能狀態對整個發動機的性能衰退情況起主導作用.因此，將氣路性能參數中的多個監測參數作為研究對象，表征發動機健康狀態.

文中將氣路性能參數中的8個表征參數[1]作為衡量發動機健康狀況的決定參數.這8個參數為：低壓壓縮機出口總溫(T24)；高壓壓縮機出口總溫(T30)；排氣溫度(T50)；風扇出口總壓(P15)；高壓壓縮機出口總壓(P30)；低壓轉子轉速(Nf)；高壓轉子轉速(Nc)；燃油流量比(phi).這些參數主要是溫度、壓力、轉速、流量相關的參數，在發動機性能出現衰退時，往往呈現較為明顯的變化，如溫度上升、壓力下降、轉速加快、流量降低.

1.1 性能衰退趨勢分析

以NASA發布的一組數據為例[2]，研究發動機性能衰退的階段性特點，各個參數檢測序列見圖1.

圖1中各個監測參數的監測值隨時間變化的規律都表明，在某一點前，數值變化慢，而達到一定值之后，數值變化增快，預示著發動機在短期內將出現失效的情況.監測參數是發動機健康狀況的表征.因此，發動機性能衰退趨勢具有與各個監測參數類似的變化特點——階段性衰退特征.

圖1 氣路監測參數的監測序列

1.2 監測參數的階段劃分方法

對監測參數進行階段劃分是突變檢測的過程，對于非平穩非線性的監測序列進行突變檢測時，采用啟發式分割算法[3-4].算法描述如下.

SD=

(1)

(2)

式中：N1，N2分別為i點前半部分與后半部分的點的總數；u1(i)，u2(i)分別為i點前半部分與后半部分的均值；S1(i)，S2(i)分別為i點前半部分與后半部分的標準偏差；SD(i)為合并偏差；T(i)為檢驗統計值.

該算法是將非平穩時間序列每個點的左右兩部分進行比較，計算T(i)，T(i)值最大時，表明該點的左右2部分的分布函數的參數具有較大差異.最大T(i)對應的i點即為該非平穩時間序列的突變點.參數在不同時間窗內具有不同的變化率可準確描述發動機性能衰退的階段性特性.

2 分階段非線性融合

從航空發動機結構的復雜性考慮，線性融合不能反映出各個監測參數與發動機健康指標(health index，HI)之間非線性的映射關系.為解決該問題，提出了分階段非線性融合的方法.分階段非線性融合是指：采用分階段的處理方式進行多參數的融合，融合模型采用非線性模型組.分階段非線性融合模型組描述為

(3)

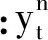
(4)

式中：Xk1為前5個循環時的HI為1對應的性能參數監測值樣本；XkB1為第1個突變點附近5個循環時HI為kB1對應的性能參數監測值樣本；XkBn為第n個突變點附近5個循環時HI為k對應的性能參數監測值樣本；Xk0為后5個循環時HI為0對應的性能參數監測值樣本；k1=[1,1,1,1,1]T；kAn=(1-mAn)I；k0=[0,0,0,0,0]T.

3 發動機性能衰退預測

3.1 性能衰退建模

多項式函數具有逼近任意非線性函數的能力，文中采用以下衰退模型對航空發動機進行性能衰退建模

(5)

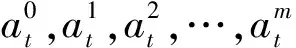
將航空發動機的性能衰退模型式(5)離散化，建立狀態空間模型[6-7]如下.

(6)

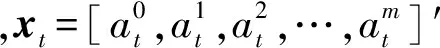
3.2 粒子濾波估計時變參數

粒子濾波算法[8]中，首先對樣本進行采樣獲得粒子，然后計算這些例子的權值，根據權值大小決定留下哪些粒子刪除哪些粒子，最后根據留下的粒子來逼近后驗概率分布，如果留下的粒子不符合要求則對這些帶權值的粒子進行第二次采樣，如此循環直到完成當前狀態的估計.

采用粒子濾波算法更新時變參數的計算過程：

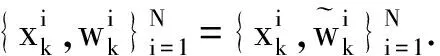
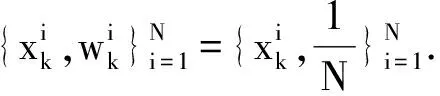
3.3 發動機剩余壽命預測步驟

基于分階段非線性融合的粒子濾波預測發動機剩余壽命的算法步驟：

步驟1 分別對多個監測參數進行突變點檢測，計算各個監測參數監測值的退化比例，得到平均突變點及突變點處的退化比例.

步驟2 以突變點對各個監測參數進行階段劃分，結合退化比例，利用訓練樣本集訓練與樣本數據對非線性融合模型進行訓練，得到不同時間窗內的融合模型系數.

步驟3 結合各個參數在全壽命周期的觀測值，利用非線性融合模型，融合得到發動機全壽命周期的HI序列.

步驟4 將由觀測值融合得到的全壽命周期健康指數序列引入到性能衰退模型中，結合粒子濾波估計以及一般擬合方法，對全壽命周期的健康指數進行最佳擬合，以確定性能衰退模型的非時變參數.

步驟5 結合各個監測參數在運行中的參數觀測值，采用非線性融合模型對多個監測參數進行融合，融合得到運行中發動機的HI序列.

步驟6 將由觀測值融合得到的運行中HI引入性能衰退模型中，采用粒子濾波估計其時變參數.將時變參數與第四步中的非時變參數代入性能衰退模型中，預測發動機失效時間，最終計算剩余壽命.

4 預測示例與算法比較

示例數據來自NASA發布的C-MAPSS的100臺發動機性能衰退數據.每臺發動機都有3個數據集：訓練集、測試集、實際RUL集.

4.1 分階段非線性融合的粒子濾波預測示例

設置粒子數為1 000，粒子的初始權值為1/1 000.選擇編號17的發動機作為預測對象.模型參數初始值分別為

步驟1 采用式(1)～(2)分別對8個參數的監測序列進行突變點檢測，計算突變點平均位置為218飛行循環時，對應的HI值為0.654 5.

步驟2 利用式(3)訓練模型系數.發動機的前5個循環時的健康指數設為1，突變點前后的5個循環時的健康指數為0.654 5，最后5個循環時的健康指數設為0，根據式(4)確定訓練樣本集：

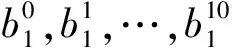
-0.000 01,-0.000 1,0.000 6,0.000 4,

-0.000 1,-0.003 3,-0.001 4,-55.252 9)

-0.000 1,-0.000 01,0.001 1,-0.000 01,

-0.000 1,-0.003 5,-0.000 3,-66.184 1)

步驟3 結合分段的非線性融合模型與模型系數，利用式(3)融合8個監測參數的監測數值，得到發動機基于分階段非線性融合的HI，見圖2.

步驟4 將狀態空間方法與粒子濾波算法相結合，進行最佳擬合.預測值(曲線①)及實際值(曲線②)見圖3.

圖2 分階段非線性融合的HI

根據發動機健康指數的最佳擬合結果，擬合誤差均值為0.042 3，確定退化方程為

步驟5 利用分階段非線性的模型系數融合得到運行中發動機的HI序列，計算結果見圖4.

步驟6 將健康指數序列作為粒子濾波算法的輸入量估計模型未來時刻的時變參數.對未來時刻的健康指數進行預測，最終得到發動機失效時間，見圖5.

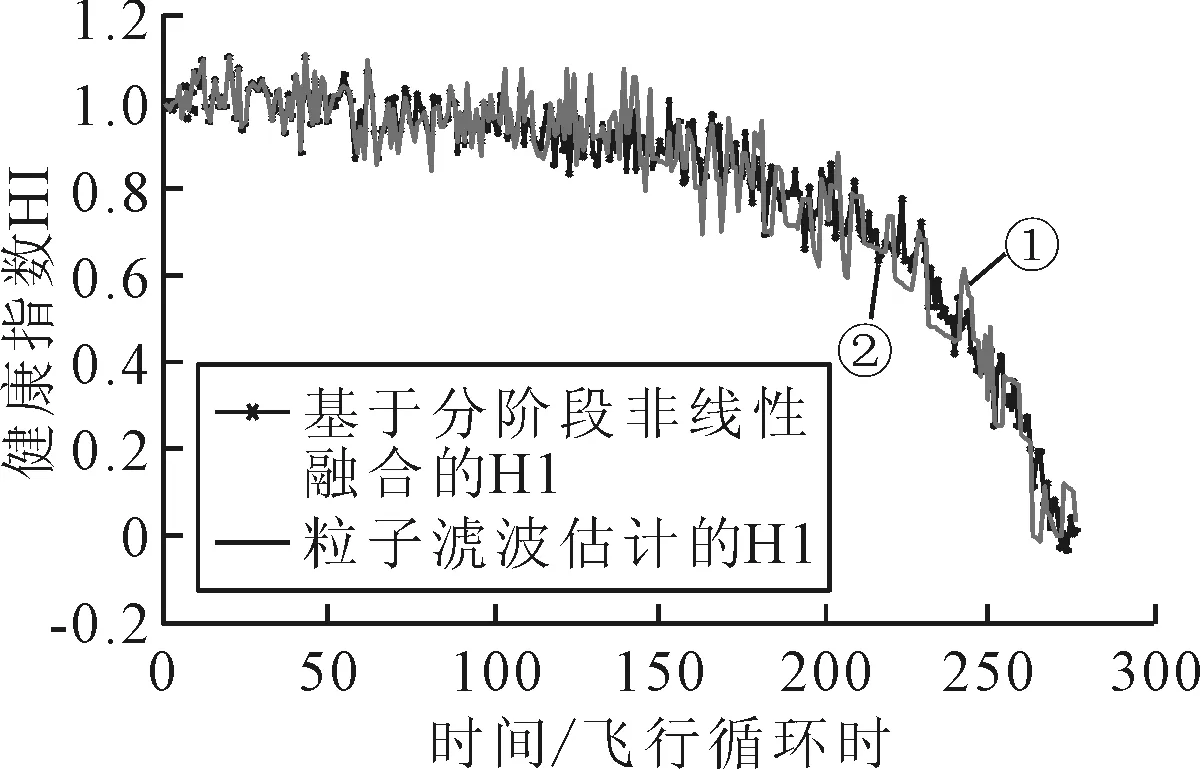
圖3 粒子濾波最佳擬合

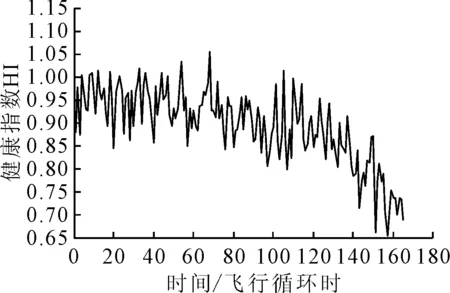
圖4 運行中發動機的HI序列

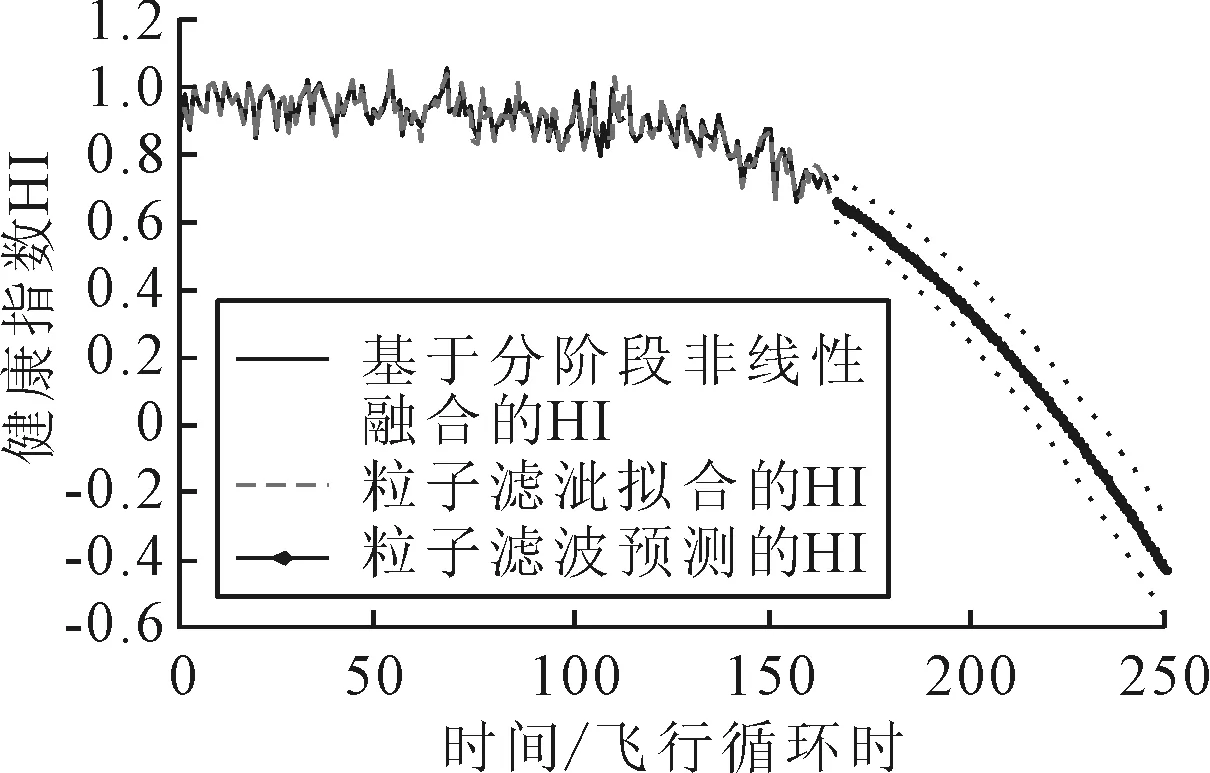
圖5 發動機剩余壽命預測

結果顯示，編號17的發動機的RUL為56.RUL數據集顯示，編號17的發動機的實際RUL為59，預測誤差為3.

4.2 算法比較

1) 擬合誤差 對編號17的發動機采用基于單階段線性融合的Kalman濾波預測、基于分階段非線性融合的粒子濾波預測發動機剩余壽命，擬合誤差結果見表1.

表1 擬合誤差比較

由表1可知，基于分階段非線性融合的粒子濾波預測在擬合過程中產生的擬合誤差均值較小.

2) 預測誤差 對編號17的發動機采用基于單階段線性融合的粒子濾波預測，基于分階段線性融合的粒子濾波預測與基于分階段非線性融合的粒子濾波預測估計RUL，預測誤差見表2.

表2中，MAPE(平均絕對百分誤差)計算公式如下.

表2 預測誤差比較

(7)

式中：Yactual為實際的剩余使用壽命；Ypredicted為預測的剩余使用壽命.MAPE越小說明預測的結果越精確.表2表明，基于分階段非線性融合的粒子濾波預測具有較高的預測精度.

3) 預測演化過程 預測演化過程是在不同的剩余壽命階段預測RUL.基于單階段線性融合的Kalman濾波預測與基于分階段非線性融合的粒子濾波預測的預測演化過程見圖6.

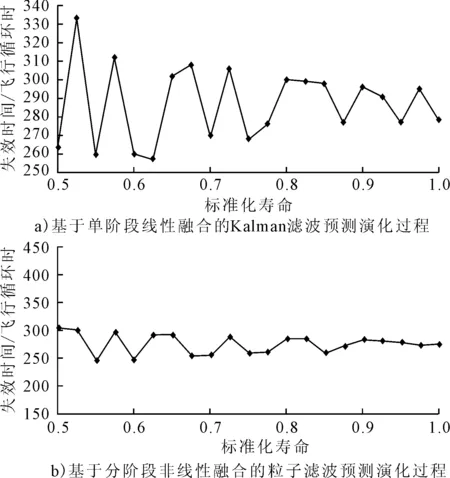
圖6 預測演化過程對比

標準化壽命的計算公式

LS=NM/LT

(8)

式中：LS為標準化壽命；NM為觀測值個數；LT為總體壽命.

隨著監測數據的引入，擬合條件越來越充分，預測的結果也越來越逼近真實值，但二者的預測演化過程存在很大差異.基于分階段非線性融合的粒子濾波預測演化過程的波動性更小，性能衰退后期逼近真實RUL的速度較快.

綜上所述，基于分階段非線性融合的粒子濾波預測方法具有擬合誤差小、預測精度高以及預測演化過程優的特點，因此，優于基于單階段線性融合的Kalman濾波預測.

5 結 論

1) 分階段的處理方式考慮了發動機的性能衰退過程的階段化特征.

2) 非線性融合的方法考慮了各個監測參數與發動機健康水平(HI)間的非線性映射關系.

3) 粒子濾波預測不以線性假設為前提，更符合發動機復雜系統的實際情況.

因此，基于分階段非線性融合的粒子濾波預測算法能夠提高發動機剩余壽命的預測精度.

[1]LIU K, GEBRAEEL N Z, SHI J. A data-level fusion model for developing composite health indices for degradation modeling and prognostic analysis[J].IEEE Transactions on Automation Science and Engineering,2013,10(3):652-664.

[2]SAXENA A, GOEBEL K. Turbofan engine degradation simulation data set[EB/OL].[2013-09-12]http://ti.arc.nasa.gov/project/prognostic-data-repository.

[3]BECK C, COHEN E G D. Superstatistics[J]. Physica A: Statistical Mechanics and Its Applications,2003,322:267-275.

[4]楊越,胡漢平,熊偉,等.一種基于超統計理論的非平穩時間序列異常點檢測方法研究[J].計算機科學,2011,38(6):93-95.

[5]LIU J Q, ZHANG M L, ZUO H F, et al. Remaining useful life prognostics for aeroenginebased on superstatistics and information fusion[J]. Chinese Journal of Aeronautics,2014,27(5):1086-1096.

[6]任淑紅.民航發動機性能可靠性評估與在翼壽命預測方法研究[D].南京：南京航空航天大學,2010.

[7]王華偉,吳海橋.基于信息融合的航空發動機剩余壽命預測[J].航空動力學報,2012,27(12):2749-2755.

[8]ZIO E, PELONI G. Particle filtering prognostic estimation of the remaining useful life of nonlinear components[J]. Reliability Engineering & System Safety,2011,96(3):403-409.

Particle Filter Prognostics Algorithm Based on Multi-phase and Non-linear Fusion

ZHANG Malan

(AVICAircraftResearchandDevelopmentCenter,Xi’an710089,China)

A fusion technique taking into account the multi-phase and non-linear characteristics of the aero-engine degradation is adopted to calculate the health level of the aero-engine. A performance model is established based on the thoughts of particle filter and the time-varying parameters of the model are estimated by particle filter algorithm. In addition, the remaining useful life of aero-engine is effectively predicted, which may attribute to the research of remaining useful life prognostics for aero-engine.

aero-engine; fusion; particle filter; remaining useful life prognostics

2016-10-03

V23

10.3963/j.issn.2095-3844.2016.06.032

張馬蘭(1990—):女，碩士，主要研究領域為航空發動機預測與健康管理