三通道非同時可控彈射座椅控制通道解耦算法研究

張明環, 宋征璽, 吳銘

(1.西北工業大學 航天學院, 陜西 西安 710072; 2.航宇救生裝備有限公司, 湖北 襄陽 441003)

三通道非同時可控彈射座椅控制通道解耦算法研究

張明環1, 宋征璽1, 吳銘2

(1.西北工業大學 航天學院, 陜西 西安 710072; 2.航宇救生裝備有限公司, 湖北 襄陽 441003)

研究了一種基于“H”形火箭包的彈射座椅控制通道解耦算法。介紹了三通道非同時可控約束條件下，基于矛盾方程組求解技術的彈射座椅控制通道解耦算法的設計與實現。在Matlab/Simulink平臺上基于4種不同需求的約束條件進行了仿真驗證，分析了解耦算法中約束條件及閾值的設定對座椅控制通道解耦效果的影響。仿真結果表明，基于“H”形火箭包的彈射座椅控制通道解耦算法在滿足所有約束條件的同時，能夠將各控制通道耦合力矩限制到主力矩的10%以下，因此證明了新算法具有較高的可信性和實用性。

彈射座椅；控制通道；三通道非同時可控；解耦；MATLAB；仿真

第4代彈射座椅的首要任務是解決低空不利姿態下的彈射救生問題[1-3]，其核心在于推力矢量的連續控制技術的應用，即通過推力矢量的快速切換，實現對座椅姿態的快速控制，使彈射座椅能夠迅速獲得盡可能大的升力，從而使座椅軌跡能夠盡可能遠離地面，即增加彈射救生高度，提升飛行員的安全性[4-5]。美國自20世紀70年代就著手第4代彈射座椅的研制，但由于推力矢量連續控制技術瓶頸，目前仍未實現工程化[6-8]。為了解決這一問題，為第4代座椅控制技術的推進提供理論基礎，在20世紀90年代末，美國以ACES Ⅱ座椅為原型，提出了以“H”形火箭包為動力基礎的第四代彈射座椅概念[9]。“H”形火箭包能夠使座椅具備姿態的快速自適應控制能力，有效彌補第3代座椅在推力矢量連續控制技術方面的缺陷，滿足第4代座椅姿態自適應控制技術的需要。然而，由于“H”形火箭包動力執行機構的工作模式限制，導致工程應用面臨一些復雜因素，其中最主要的難點在于，為了保證內部壓力的平衡，“H”形火箭包所配置的4個噴口采用了兩兩對偶的工作方式，利用2對噴口間的推力差來產生彈射座椅姿態控制所需的控制力和控制力矩。雖然該模式能夠滿足推力矢量連續控制的需求，但也將使控制系統的3個通道無法同時可控，進而導致單通道姿態控制時存在其它兩個方向的耦合控制力矩，無法滿足控制系統設計需求。本文將針對“H”形火箭包特殊的工作方式，通過對4個噴口安裝角度進行優化計算，實現控制系統三通道的力矩解耦，從而為以“H”形火箭包為動力基礎的第4代彈射座椅姿態控制系統的設計提供可行性。

1 “H”形火箭包動力模型

根據相關文獻及航宇救生裝備有限公司所提供的技術資料[10]，“H”形火箭包的結構如圖1所示。

圖1 “H”形火箭包結構

其中αh1、βh1、αh2、βh2為4個噴口的安裝角度,下標1表示噴口1和噴口2的安裝角度,下標2表示噴口3和噴口4的安裝角度。xc、yc為人椅系統的重心位置,Lh1、Lh2為人椅系統的尺寸。

“H”形火箭包的三通道控制模式(如圖2所示):

1) 俯仰控制模式

2) 偏航控制模式

3) 滾轉控制模式

圖2 “H”形火箭包3種工作模式

其中Fh為“H”形火箭包的總推力,K∈[0,1]為針栓位置所決定的噴口推力分配比例,Fh1、Fh2、Fh3、Fh4分別為“H”形火箭包4個噴口的推力。可以看出,“H”形火箭包是通過各噴口推力之間兩兩對稱產生推力差,從而提供座椅姿態及軌跡控制所需的控制力及控制力矩。

根據“H”形火箭包的結構和工作模式,4個噴口所提供了控制力矩為:

噴口1

(1)

噴口2

(2)

噴口3

(3)

Fh3sinαh2sinβh2·xc

Mh3z=Fh3sinαh2cosβh2·yc-Fh3cosαh2·xc

噴口4

(4)

由此,當4個噴口同時工作時,產生的總控制力矩為

(5)

當4個噴口安裝角度設計未進行優化設計時,將會在每個工作模式下都在其他2個控制通道產生耦合控制力矩,以滾轉控制模式為例,此時火箭包4個噴口在偏航和俯仰通道上產生的耦合力矩為

Mhz=-Fh1sinαh1cosβh1·(Lh1-yc)-Fh1cosαh1·

xc-Fh2sinαh1cosβh1·(Lh1-yc)-Fh2cosαh1·

xc+Fh3sinαh2cosβh2·yc-Fh3cosαh2·xc+

Fh4sinαh2cosβh2·yc-Fh4cosαh2·xc

(6)

同理,在偏航控制模式下也會存在其他2個通道的耦合控制力矩。但需要注意的是,由于“H”形火箭包的結構對稱性,在俯仰控制模式下不會存在其他2個通道的耦合控制力矩。

2 控制通道解耦算法設計

由于控制系統的三通道非同時可控,因此控制力矩的解耦原則為:

1) 進行俯仰通道控制時:要求偏航控制力矩與滾轉控制力矩同時為零;

2) 進行偏航通道控制時:要求俯仰控制力矩與滾轉控制力矩同時為零;

3) 進行滾轉通道控制時:要求俯仰控制力矩與偏航控制力矩同時為零。

以滾轉通道為例,根據(6)式的耦合力矩描述,可將解耦需求轉化為

(7)

(8)

由于控制力矩的解耦應與推力大小無關,因此(8)式所描述的解耦方程可進一步轉化為

(9)

同理,可獲得偏航通道的解耦需求

(10)

聯立(9)式和(10)式可得控制力矩解耦矛盾方程組

(11)

為了克服氣動干擾,保證姿態控制系統的可控性,需設置最大控制力矩約束條件

(12)

Mmin表示為滿足系統可控性和快速性要求下,各控制通道所需的最小力矩。

另外,由于彈射座椅姿態控制的目標是提升彈射高度,因此在解耦方程中應加上最大升力約束條件

(13)

L表示座椅理想姿態下獲得的升力,Lmin表示為滿足GJB1800A救生性能要求,在座椅理想姿態下,“H”形火箭包所需提供的最小升力,Lmin可由GJB1800A中所給出了救生性能包線計算得出。

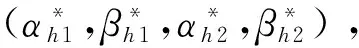
(14)

通過對閾值ε的設定,可以對“H”形火箭包4個噴口的安裝角度進行篩選優化,從而完成控制系統三通道的力矩解耦。

3 仿真結果及分析

為了驗證約束函數的合理性及解耦算法的有效性,本文將側重不同優化目標設計4組仿真實驗:

1) 升力優先

解耦約束函數為:|Mhx|≥1 500 Nm,|Mhy|≥1 500 Nm,|Mhz|≥1 500 Nm,L=13 000 N

2) 滾轉控制力矩優先

解耦約束函數為:|Mhx|≥3 000 Nm,|Mhy|≥1 500 Nm,|Mhz|≥1 500 Nm,L=12 000 N

3) 偏航控制力矩優先

解耦約束函數為:|Mhx|≥1 500 Nm,|Mhy|≥3 000 Nm,|Mhz|≥1 500 Nm,L=12 000 N

4) 俯仰控制力矩優先

解耦約束函數為:|Mhx|≥1 500 Nm,|Mhy|≥1 500 Nm,|Mhz|≥3 000 Nm,L=12 000 N

仿真結果如表1～表8所示:

1) 升力優先

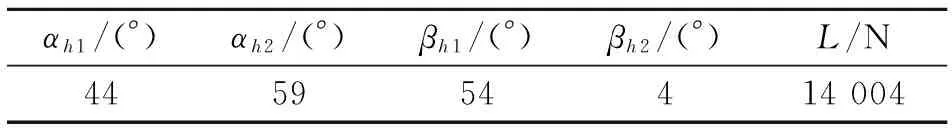
表1 升力優先噴口安裝角度解耦結果

表2 升力優先控制通道解耦結果

2) 滾轉控制力矩優先

表3 滾轉控制力矩優先噴口安裝角度解耦結果

表4 滾轉控制力矩優先控制通道解耦結果

3) 偏航控制力矩優先

表5 偏航控制力矩優先噴口安裝角度解耦結果

表6 偏航控制力矩優先控制通道解耦結果

4) 俯仰控制力矩優先

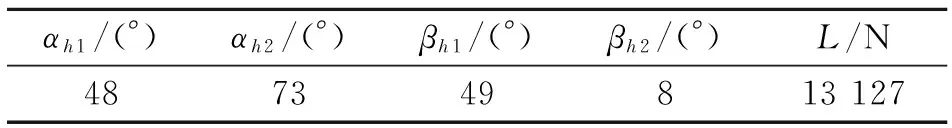
表7 俯仰控制力矩優先噴口安裝角度解耦結果

表8 俯仰控制力矩優先控制通道解耦結果

從表1、表3、表5和表7可以看出,經過噴口安裝角度優化配置,座椅理想姿態下可獲得的升力滿足了最大升力約束條件的要求,而從表2、表4、表6和表8可以看出,各控制通道的主力矩也都滿足了最大控制力矩約束條件的要求。

另外從表2、表4、表6和表8還可以看出,經過噴口安裝角度優化配置,滾轉和偏航通道工作時所產生的耦合控制力矩遠小于控制通道的主力矩,而俯仰通道則由于“H”形火箭包總體結構的對稱性,控制通道間并不存在耦合力矩。

需要注意的是,在仿真實驗1)中,為了保證最大升力約束條件的苛刻要求,仿真時適當放大了矛盾方程組中閾值ε,滾轉和偏航通道中的耦合力矩因而稍微偏大,但仍然比主力矩小一個數量級,因此并不影響解耦效果。

而在仿真實驗2)、3)、4)中,由于最大控制力矩約束條件不如最大升力約束條件苛刻,矛盾方程組中閾值ε設定在一個較小的值上,滾轉和偏航通道中的耦合力矩因而較小,被限制在主力矩的10%以內,解耦效果更優。

綜上所述,本文通過對約束條件下矛盾方程組的求解完成“H”形火箭包4個噴口安裝角度的優化,良好的仿真結果表明,本文設計的控制通道解耦算法能夠很好的實現控制系統三通道的力矩解耦,為彈射座椅姿態控制系統的設計提供了可行性。

4 結 論

本文基于“H”形火箭包的特殊結構,建立了其動力模型。在此基礎上,根據“H”形火箭包工作模式的特點,基于約束條件下矛盾方程組的求解過程,設計了三通道非同時可控彈射座椅控制通道解耦算法,以實現控制系統三通道的力矩解耦,為彈射座椅自適應控制系統的深化設計提供了理論上的可行性。

通過仿真分析,研究了不同約束條件對控制通道解耦效果的影響,并以矛盾方程組的求解閾值為調節手段,對約束條件和耦合力矩間的關系進行了深入分析。仿真結果表明,即便在較為苛刻的約束條件下,本文所設計的控制通道解耦算法仍然能夠將各控制通道耦合力矩限制到主力矩的10%以下,因此證明了本文算法具有較高的可信性和實用性。

[1] Wang Y F, Han L L, Wang F. Review of Ejection Seat Electronic Program Controller[J]. Applied Mechanics and Materials, 2014(551): 530-534

[2] Miles J E. Factors Associated with Delayed Ejection in Mishaps Between 1993 and 2013[J]. Aerospace Medicine and Human Performance, 2015, 86(8): 774-781

[3] Wang Y F, Chen G, Han L L. The Comprehensive Survey for the Numerical Simulation of the 4th Generation Rocket Ejection Seat Thrust Vector Control System[J]. Design, Manufacturing and Mechatronics, 2014(551): 523-529

[4] 郁嘉,林貴平,毛曉東. 彈射救生數值仿真及不利姿態下救生性能分析[J]. 航空學報, 2010, 31(10): 1927-1932 Yu Jia, Lin Guiping, Mao Xiaodong. Numerical Simulation of Ejection Seat and Analysis of Performance under Adverse Attitudes[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(10): 1927-1932 (in Chinese)

[5] 蔣偉. 基于Matlab彈射救生系統全過程仿真研究[D]. 南京:南京航空航天大學,2012 Jiang Wei. The Whole Trajectory Simulation Research of Ejection Seat and Occupant System with Matlab[D]. Nanjing, Nanjing University of Aeronautics and Astronautics, 2012 (in Chinese)

[6] Guan H, Zhu Y, Zhao X, et al. Aerodynamic Characteristics of Ejection Seat and Occupant[C] ∥51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 2013

[7] Mao X D, Lin G P, Yu J. Predicting Ejection Velocity of Ejection Seat via Back Propagation Neural Network[J]. Journal of Aircraft, 2011, 48(2): 668-672

[8] Zhu Y, Guan H, Zhao X, et al. Computational Studies of Jettisoned Canopy and Ejection Occupant/Seat[C]∥50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 2012

[9] Blairnald A. 4th Generation Escape System Technologies Demonstration Phase II[R]. Generation Escape System Technologies Demonstration Phase II, 1998

[10] 吳銘.自適應座椅仿真數學模型研究報告[R]. 襄陽:航宇救生裝備有限公司,2013 Wu Ming. Research Report of the Simulation Model of the Adaptive Seats[R]. Xiangyang, Aerospace Life-Support Industries, LTD, 2013 (in Chinese)

Control Channel Decoupling Algorithm for Ejection Seat Subject to Three Channels Non-Simultaneous Controllable

Zhang Minghuan1, Song Zhengxi2, Wu Ming2

1.School of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China 2.Aerospace Life-Support Industries, LTD, Xiangyang 441003, China

A control channel decoupling algorithm for “H” structure of ejection seats is presented in this paper. Under the constraint condition of three channels non-simultaneous controllable, the decoupling algorithm is designed based on contradiction equations solution. The simulation is achieved under Matlab/Simulink in accordance with 4 different constraint conditions. The influence of the constraint condition and the threshold value in contradiction equations are analyzed. The simulation results and their analysis show that, under all the constraint conditions, the decoupling algorithm for “H” structure of ejection seats can reduce each coupling moment to 10 percents of the corresponding main moment, thus proving the algorithm in this paper to be reliable and effective.

ejection seats; control channel; three channel Non-Simultaneous controllable; decoupling; MATLAB; simulation

2016-05-12

航天支撐基金(N2015KC0121)資助

張明環(1985—)，西北工業大學助理研究員，主要從事飛行器控制系統設計與仿真研究。

V244.21+2

A

1000-2758(2016)06-0957-06