水下通信用光纜線包纏繞力學建模及仿真

湯偉江, 劉衛東, 陳剛, 楊賀然, 張建軍

1.西北工業大學 航海學院, 陜西 西安 710072; 2.中國船舶重工集團公司第705研究所, 陜西 西安 710077;3.西北工業大學 水下信息與控制重點實驗室, 陜西 西安 710072

水下通信用光纜線包纏繞力學建模及仿真

湯偉江1,2, 劉衛東1,3, 陳剛2, 楊賀然2, 張建軍1

1.西北工業大學 航海學院, 陜西 西安 710072; 2.中國船舶重工集團公司第705研究所, 陜西 西安 710077;3.西北工業大學 水下信息與控制重點實驗室, 陜西 西安 710072

因電磁波無法在水中傳播,水下大容量長距離通信僅能依靠光纜等有線通信方式。對于水下航行器等需隨航行體運動實時布放光纜以建立動態通信信道的應用場合,光纜線包纏繞工藝及纏繞機構的優化設計,對減小斷線概率、提高水下通信的可靠性顯得尤為重要。在對光纜纏繞過程及端板力學分析的基礎上,提出一種以各層光纜徑向變形和軸向變形為增量的逐層分析方法,建立了水下通信用光纜線包纏繞力學模型。該模型揭示了纏繞過程光纜線包內張力分布及端板變形的內在規律,以實際光纜線包結構參數和纏繞工藝參數對光纜線包內部應變、光纜層壓強以及端板變形進行仿真分析,仿真結果與光纜線包纏繞過程應變實測數據符合性好。

水下航行器;光纜線包;纏繞力學模型;光纜軸向應變;端板變形

光纖通信是水下系統實現遠程大容量通信的優選通信方式。將光纖通信技術應用于水下航行器,有利于實現其與母船的雙向大容量信息傳輸,而水下航行器要求實時布放與之運動相匹配的光纜,以建立動態可靠通信信道。光纜線包是水下航行器光纜布放系統的核心部件,由單根光纜分層緊密纏繞而成,纏繞時需對光纜施加一定的纏繞張力,以使光纜能在一定張緊條件下繞入線包,纏繞張力的存在使光纜線包各層光纜存在內張力,內張力的分布狀態影響光纜線包的整體性及在大深度水下的使用性能;內張力的存在使光纖產生應力,決定光纜線包的使用及貯存壽命[1];光纜線包纏繞時,各層光纜因徑向受壓會產生軸向變形,進而導致纏繞過程兩側端板的變形,在安裝殼體并去除芯軸后,端板變形恢復會引起線包內部開裂甚至塌方,大幅降低光纜線包的布放性能。因此,準確分析纏繞過程光纜的內張力以及對端板施加的軸向力分布,可指導光纜線包纏繞工藝及纏繞機構的設計。

國內外學者對纖維增強復合材料、大揚程起重設備的鋼絲繩、導彈用制導光纜線包纏繞等纏繞力學特性領域已開展了相關研究工作并取得了一些成果。針對纖維增強復合材料纏繞力學特性的研究主要是利用復合材料的三維本構關系,建立內襯及各層纖維的應力應變模型,分析內襯和各層復合材料應力[2-3]以及內襯厚度[4]、纏繞角度[5]和纏繞張力[6-8]對應力分布的影響并研究纏繞張力的設計方法。胡勇等針對雙折線卷筒鋼絲繩的排列方式,建立了鋼絲繩多層纏繞系數方程,并對多層纏繞系數及內張力分布進行了仿真[9],由于鋼絲繩的松散纏繞特性,并未考慮同層鋼絲繩匝與匝之間的相互作用。馬成舉等建立了導彈用制導光纜線包層間壓強模型,在模型中以卷盤徑向收縮形變系數常量來表示纏繞過程卷盤和光纜層的變形,并對纏繞過程光纜層壓強進行仿真分析和實驗驗證[10]。

鋼絲繩纏繞為松散纏繞,復合材料及導彈用制導光纜纏繞架均沒有兩側端板,而水下航行器光纜線包為分層雙向緊密纏繞,纏繞架由芯軸和兩側端板組成,其纏繞方式、纏繞架結構與上述研究有較大差異,是纏繞力學特性研究的一個新方向。在分析光纜及端板受力的基礎上,研究逐層纏繞時光纜徑向壓縮、軸向延伸與光纜內張力、軸向擠壓力的關系,建立了光纜線包纏繞力學模型;根據實際光纜線包結構參數和纏繞工藝參數,對光纜線包內部應變、光纜層壓強以及端板變形隨纏繞層數的變化規律進行了仿真研究,并利用高精度光纖應變分析儀對光纜線包的應變進行了實驗測量,通過仿真與實測數據的對比,驗證了模型的準確性。

1 光纜線包受力分析及模型建立

通過專用繞線機將單根光纜逐層緊密纏繞在纏繞架(如圖1所示)上,形成光纜線包。在纏繞過程中,當前層光纜繞入時,已繞各層光纜因擠壓而產生徑向變形,使各層光纜周向變形減小,軸向變形增大,從而使各層光纜的內張力減小、各層光纜施加在端板上的軸向擠壓力增大。端板在各層光纜對應位置的變形量與垂直于端板軸向擠壓力呈線性關系,且各層光纜的內張力與其徑向變形也呈線性關系。因此,以各層光纜徑向變形和軸向變形為增量,形成一種逐層增量分析方法,建立光纜線包纏繞力學模型,研究纏繞過程各層光纜內張力以及對端板軸向擠壓力的變化規律。

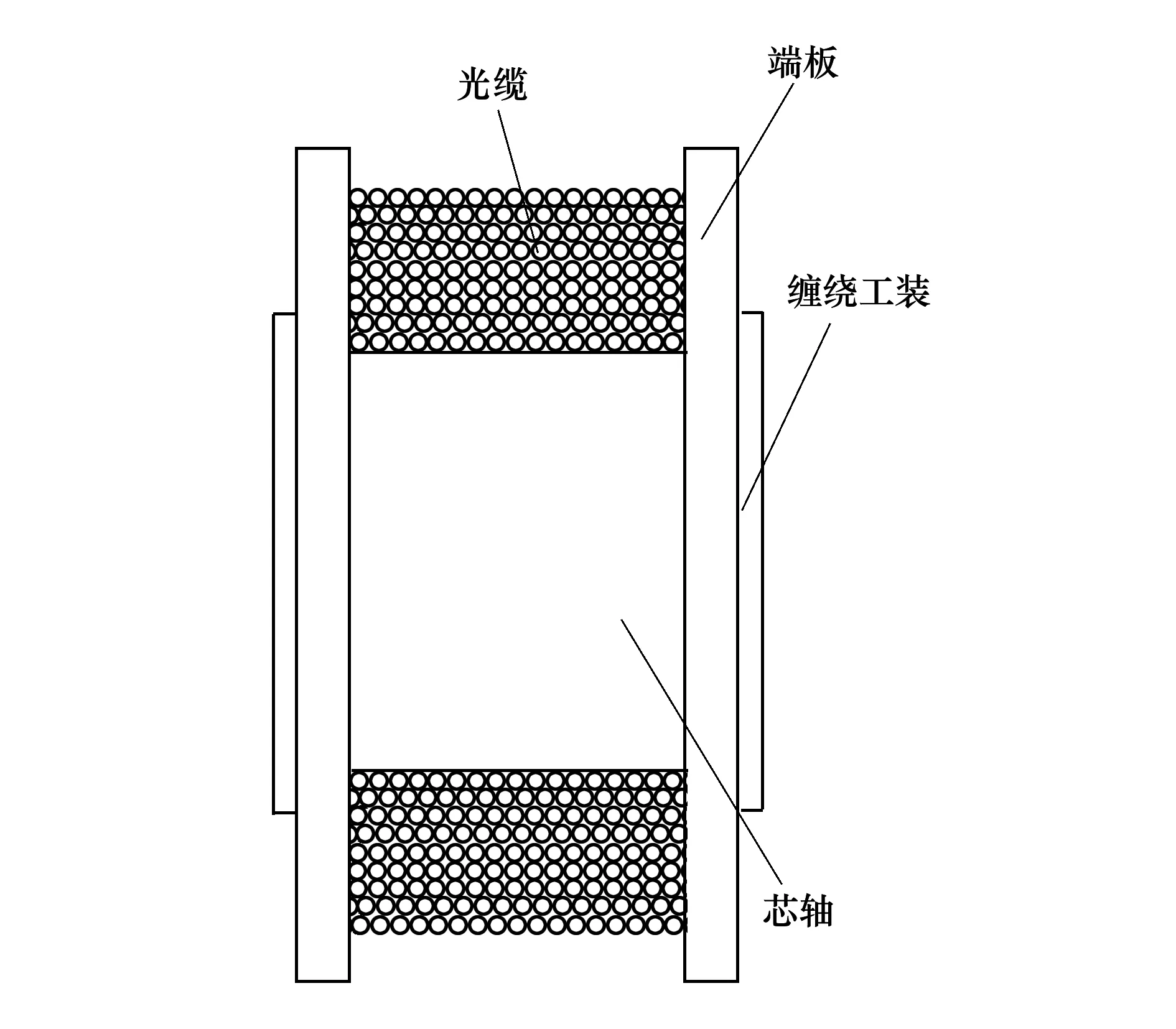
圖1 光纜線包及纏繞架結構

1.1 光纜線包受力分析

芯軸與端板之間依靠纏繞工裝固連,形成纏繞架后,端板之間位置固定。除第1層外,每層光纜均纏繞在下一層光纜匝與匝之間形成的凹槽內,纏繞當層光纜對兩側端板無軸向力作用。

纏繞第n層光纜時,第i層光纜的徑向變形量ΔRi,n與該層光纜的徑向壓縮量Δri,n、第(i-1)層徑向變形量ΔR(i-1),n和第(i-1)層光纜徑向壓縮量Δr(i-1),n相關,即

(1)

以此類推,第1層光纜僅與該層光纜徑向壓縮量Δr1,n有關,即

(2)

由此可見,纏繞第n層光纜時,各層光纜的徑向變形量與纏繞第n層光纜引起的該層及以下各層光纜的徑向壓縮量相關,而徑向壓縮量是由纏繞第n層光纜對內部各層的徑向壓力增量作用而產生的。

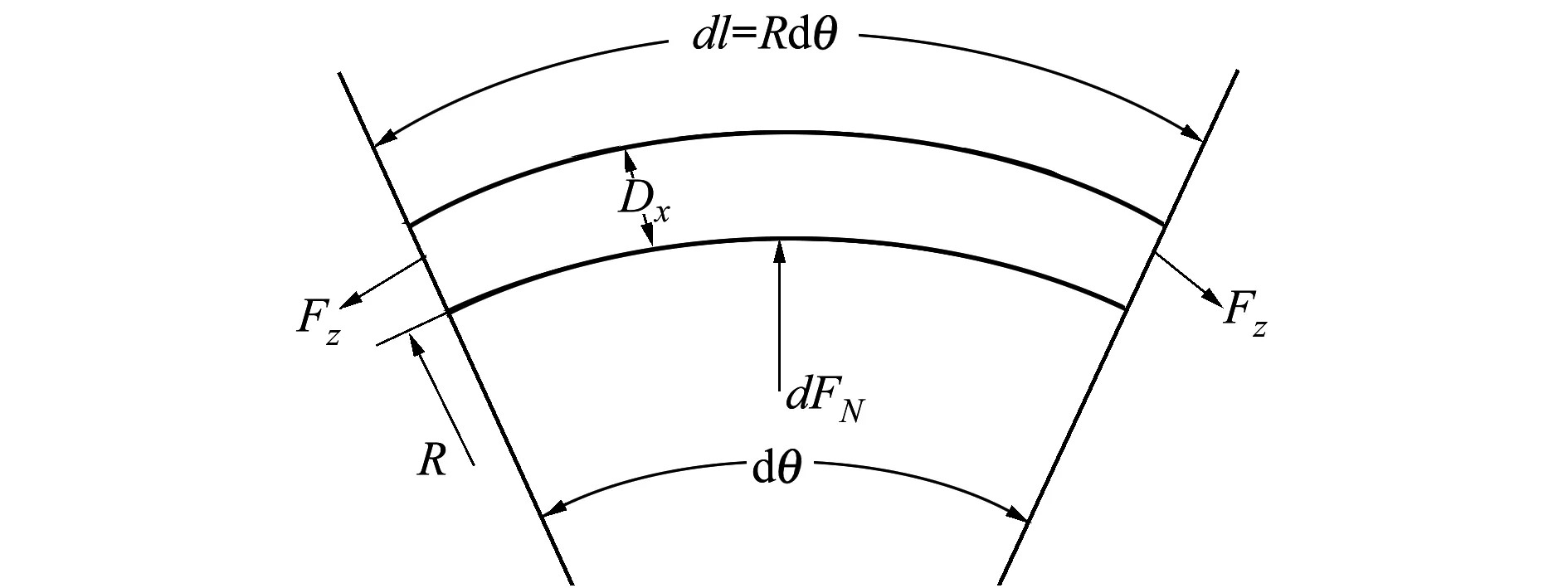
圖2 光纜微元受力

取dl長度的已繞光纜微元(如圖2所示),纏繞半徑為R,dθ為光纜微元對應的張角,Fz為光纜的纏繞張力,dFN為內層光纜施加在該層光纜的支撐力,Dx為光纜直徑。

由受力平衡可得

(3)

內層光纜所受壓強

(4)

以張角dθ對應的各層光纜微元為研究對象,第(i+1)層、第(i+2)層、…、第n層光纜對第i層光纜均有壓力,其大小為各層光纜內張力沿線包徑向的合力。當第n層光纜纏繞到線包上時,第(n-1)層光纜所受壓力增量為Fzdθ,但是第(n-1)層及以下各層光纜由于第n層光纜的纏繞,內張力分別減小ΔFz(n-1),n、ΔFz(n-2),n、…、ΔFz(i+1),n,相應的各層光纜沿線包徑向壓力的減小值分別為ΔFz(n-1),ndθ、ΔFz(n-2),ndθ、…、ΔFz(i+1),ndθ,因此由于第n層的纏繞導致第i層光纜在dθ部分所受壓力增量dFNi,n為

(5)

由于光纜線包為緊密纏繞,層與層之間變形協調,無相對滑動,層與層光纜之間無摩擦力存在,且同層光纜軸向變形也是協調的,忽略與端板接觸的光纜因徑向變形而與端板之間產生的摩擦力。

光纜截面受力如圖3所示。dFNri,n和dFNxi,n為作用在第i層光纜力的增量,而作用在第i層光纜下側力的增量應為dFNr(i-1),n和dFNx(i-1),n。這里為簡化計算將作用在第i層光纜下側力的增量近似用dFNri,n和dFNxi,n代替。

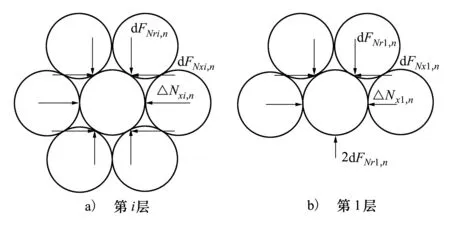
圖3 光纜截面受力

(6)

(7)

式中,γ為光纜堆疊角。

光纜徑向壓縮量為

(8)

式中,Er為光纜徑向彈性模量,是單位長度光纜承受的徑向壓力與光纜徑向直徑沿壓力方向減小量的比值,Wr為光纜徑向彈性系數,是與壓力垂直方向徑向直徑的增加量和沿壓力方向徑向直徑的減小量的比值,ΔNxi,n為纏繞第n層時第i層單位長度光纜匝與匝之間的軸向擠壓力增量(等于該層光纜對端板的軸向擠壓力增量),dli為張角dθ對應的第i層光纜微元的長度,即

(9)

式中,Ri為第i層光纜的半徑,Rz為芯軸半徑。

同理,可以獲得光纜的軸向延伸量為

(10)

1.2 端板受力分析

1) 擠壓變形

由于纏繞工裝彈性模量遠大于端板彈性模量,因此分析時可忽略纏繞工裝的變形。Rt為纏繞工裝半徑,若Rz≤Ri≤Rt(即1≤i≤nt,nt為Rt對應的光纜層數),端板受力如圖4所示。

圖4 纏繞工裝半徑范圍內端板受力

由受力平衡,可得

(11)

式中,Δqi,n為因纏繞第n層時第i層光纜軸向擠壓力增量作用下纏繞工裝作用在端板的均布壓強增量。

纏繞工裝范圍內各層光纜對端板施加的力與纏繞工裝對端板的作用力相等,即

(12)

則端板擠壓變形ΔLbi,n為

(13)

式中,Eb為端板的彈性模量,Lb為端板厚度。

2) 彎曲變形

纏繞工裝范圍以外各層光纜對端板施加的軸向擠壓力將使端板產生彎曲變形。端板滿足薄板彎曲理論的基本假設,依據圓形板對稱彎曲理論[11],有

(14)

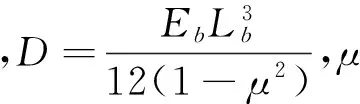
在第i層光纜軸向擠壓力作用下,Ri范圍內剪力為

(15)

將(15)式代入(14)式,可得

(16)

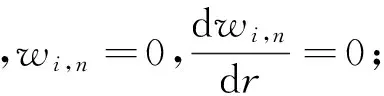
wi,n(r)=ΔNxi,nGi(r)

(17)

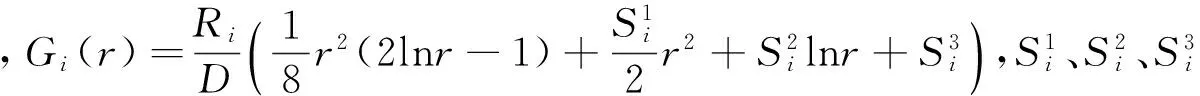
轉角αi,n(r)為

(18)

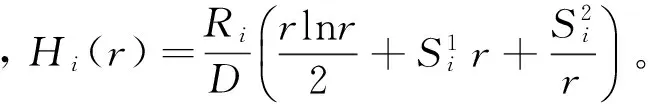
當j≤i時,由ΔNxj,n引起第i層光纜對應端板位置的撓度為

(19)

當j>i時,由ΔNxj,n引起第i層光纜對應端板位置的撓度為

w″j,i=wj,n(Ri)

(20)

由(19)式和(20)式,可得纏繞第n層時第i層光纜對應端板位置的彎曲變形為

(21)

1.3 光纜線包纏繞過程力學模型

忽略芯軸的徑向變形,第n層纏繞時第i層光纜的徑向變形導致該層光纜內張力的減小,即

(22)

式中,Ex為光纜軸向彈性模量,Ax為光纜截面面積。

假設在各層纏繞時,每層光纜均與端板接觸,即每層光纜沿線包軸向變形應等于兩側端板對應該層光纜位置的變形之和,即

(23)

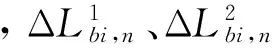
(23)式是在每層光纜均不與端板脫開的假設條件下得出的,而隨著光纜的纏繞,內層光纜的軸向擠壓力不斷增大,可能使端板對應外層光纜位置的變形大于光纜的軸向變形,因此在仿真計算時應判斷各層擠壓力增量和是否為負值(即該層端板變形是否大于光纜層軸向變形),若為負值,則應忽略該層軸向力增量影響并重新計算。

將(22)式和(23)式聯立,即可獲得纏繞第n層光纜時內部各層光纜內張力減小量以及各層光纜匝間軸向擠壓力增加量。

第i層光纜后續層的纏繞均會造成第i層光纜內張力的減小,纏繞第n層光纜后,第i層光纜內張力為

(24)

光纜內張力引起的光纜軸向應變為

%

(25)

纏繞第n層光纜后,第i層光纜所受外層光纜的壓強為

(26)

2 仿真分析

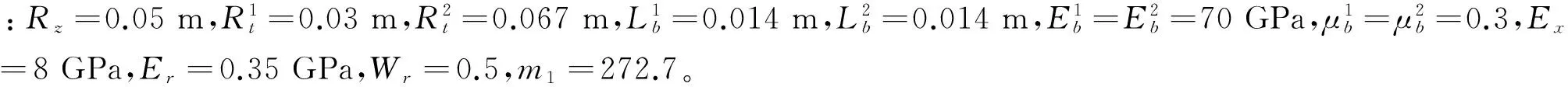
2.1 光纜內部應變分布

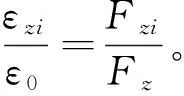
圖5 光纜內部應變分布隨纏繞層數的變化情況

2.2 光纜層壓強

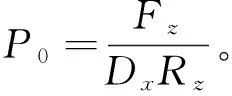
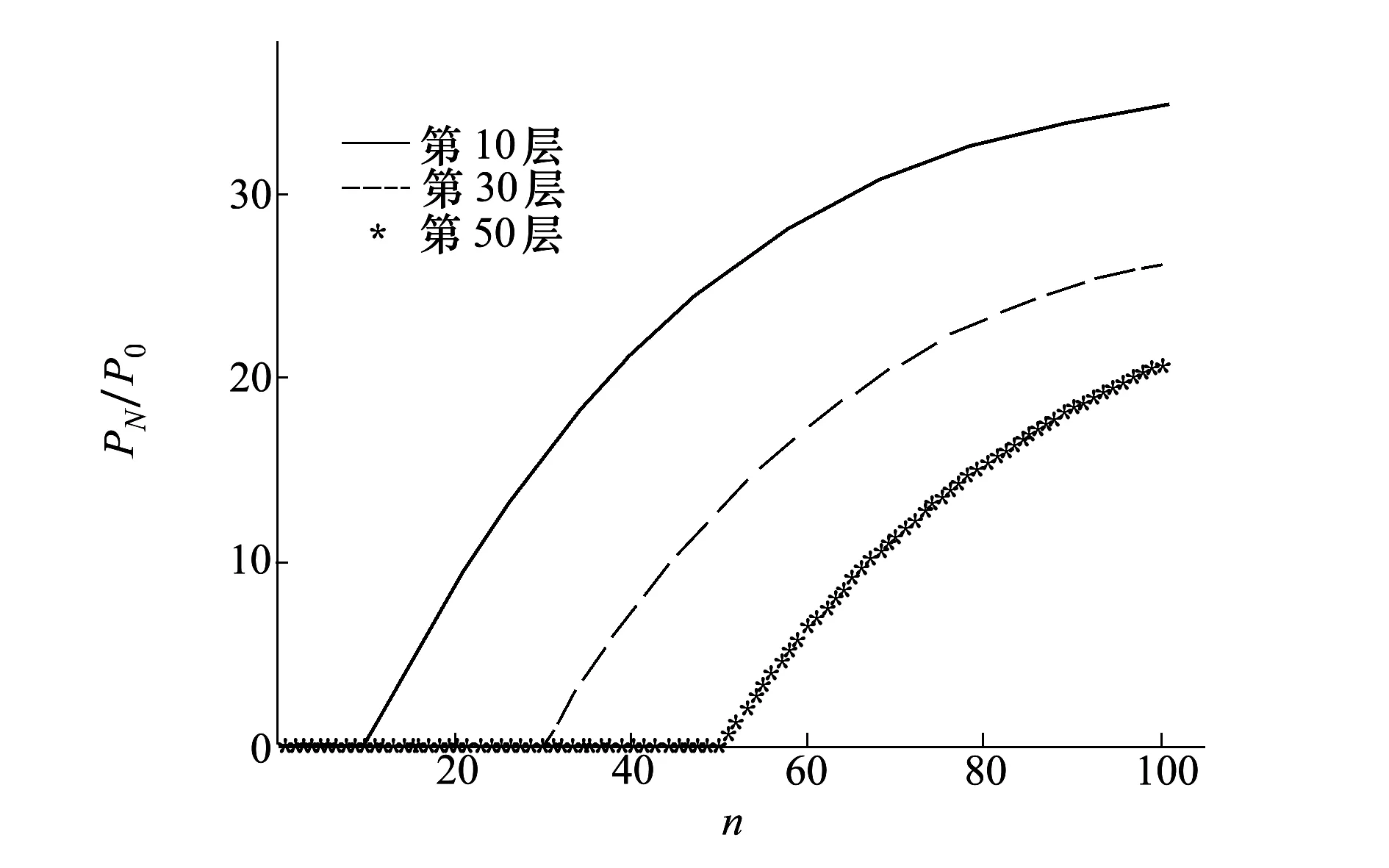
圖6 光纜層壓強隨纏繞層數的變化情況

2.3 端板變形

設兩側端板外圓直徑均為300 mm,對兩側端板外圓間距變化進行仿真(如圖7a)所示),兩側端板間距隨纏繞層數的增加而不斷增大,并逐漸趨于平穩。由于仿真采用的是鋁基體端板,彈性模量較大,光纜纏繞過程各層光纜對端板施加的軸向擠壓力引起的端板變形較小,最大端板間距變化量僅為0.012 6 mm,對去掉芯軸后的光纜線包性能影響較小。水下航行器由于自身總體性能的需求,要求光纜線包重量要輕,以非金屬替代金屬作為端板材料可有效降低光纜線包的重量,然而非金屬材料彈性模量一般遠小于金屬材料,在相同結構尺寸下以非金屬作為端板材料會導致纏繞過程端板變形較大(如圖7b)所示,最大端板間距變化量達到了1.35 mm),從而降低光纜線包的布放性能,因此需綜合考慮,在保證光纜線包性能的前提下合理選擇輕質端板材料。

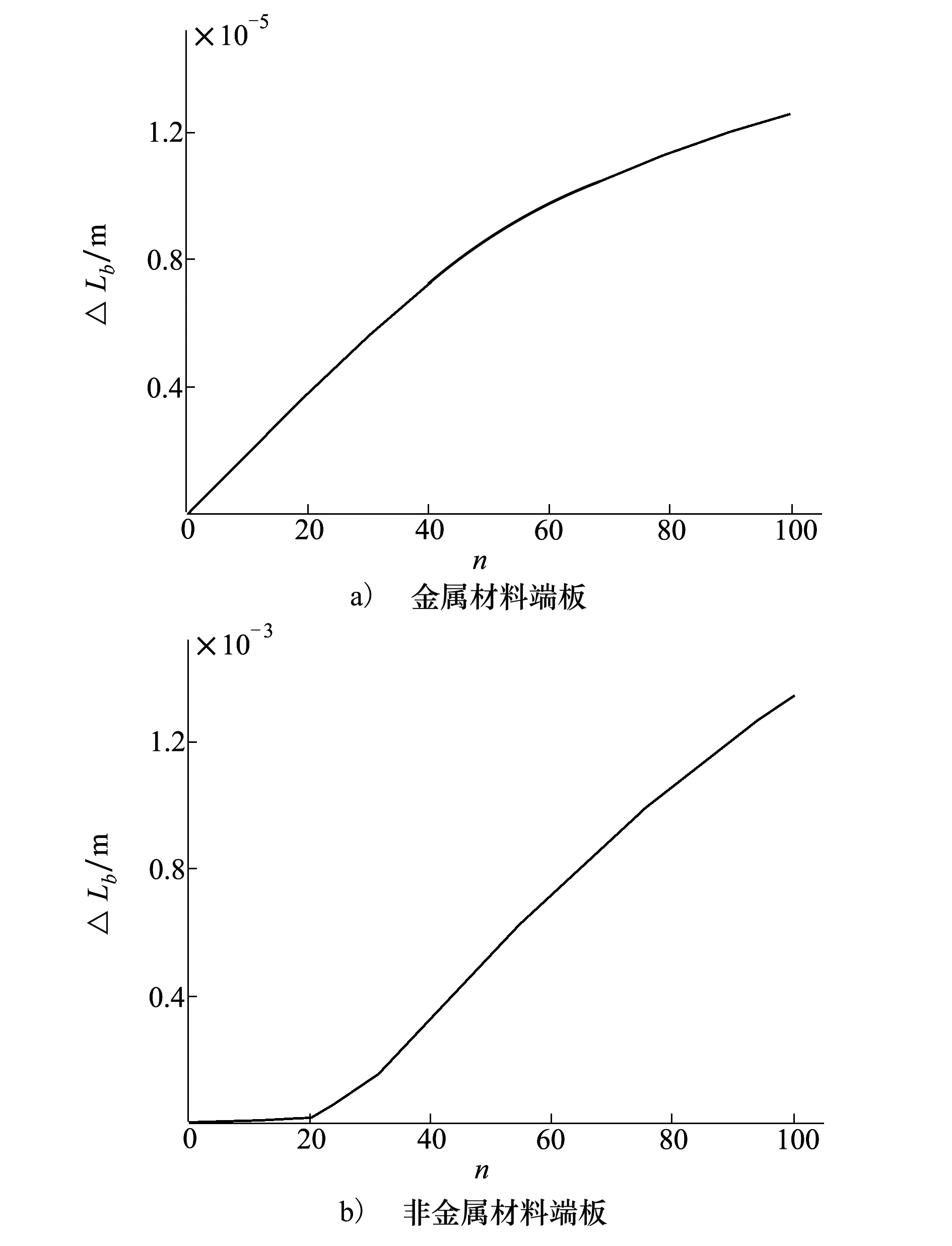
圖7 兩側端板間距變化與纏繞層數的關系

3 實驗驗證

實驗使用不同長度的2根光纜以等張力纏繞2個結構尺寸不同的光纜線包,采用AQ8603光纖應變分析儀測量光纜線包纏繞后的內部應變分布。光纖應變分析儀基于布里淵后向散射光檢測技術,通過采樣一定長度上的布里淵散射頻率漂移,獲得光纖應變分布數據。纏繞前應測量光纜內光纖的初始應變εs,2個線包分別纏繞了89層和105層。圖8為光纖應變分析儀測量的2個光纜線包纏繞后的應變曲線,是應變隨長度的變化關系,為對應模型中應變隨纏繞層數的變化,將此應變測試數據用公式(27)轉化為層均應變。

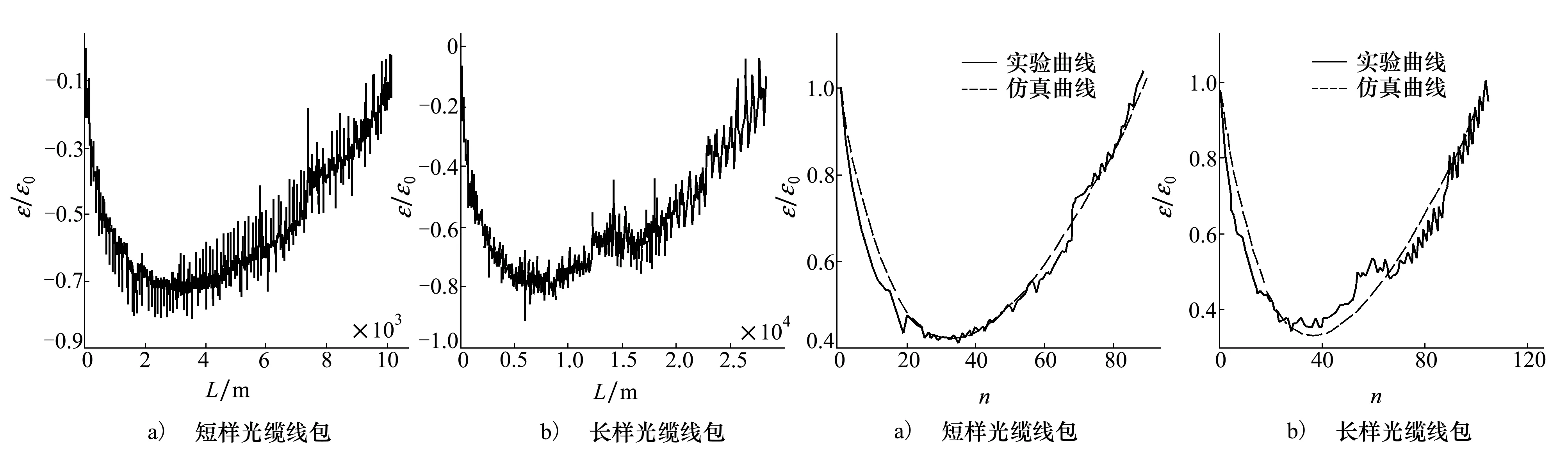
圖8 光纜線包纏繞后的應變測試曲線圖9 光纜線包內部應變仿真、實驗曲線對比

(27)

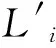
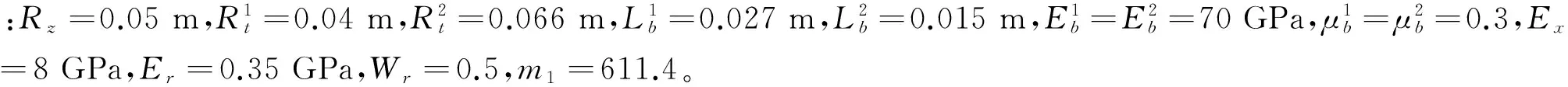
4 結 論

通過對水下航行器光纜線包光纜及端板受力進行理論分析,采用逐層分析各層光纜徑向變形和軸向變形的方法建立光纜線包纏繞力學模型,以此模型對光纜線包內部應變分布、光纜層壓強以及端板變形隨纏繞層數的變化情況進行了仿真分析,利用高精度光纖應變分析儀測量光纜線包的應變,并對實測數據與仿真結果的偏差進行了分析,研究表明,實測與仿真曲線整體趨勢一致且偏差較小,模型準確度高。本研究為水下航行器用光纜線包纏繞工藝及纏繞機構設計奠定了理論基礎,也可為其他領域光纜線包纏繞過程分析提供借鑒和參考。

[1] 王寶珠,鄧宏林,李小瑞,等. 制導光纜中光纖壽命預期[J]. 應用光學,2006,26(6):41-45 Wang Baozhu, Deng Honglin, Li Xiaorui, et al. Lifetime Prediction for the Optical Fiber in Guidance Optical Fiber[J]. Journal of Applied Optics,2006,26(6):41-45 (in Chinese)

[2] 邢靜忠,陳利,孫穎. 纖維纏繞厚壁柱形壓力容器的應力和變形[J]. 固體火箭技術,2009,32(6):680-689 Xing Jingzhong, Chen Li, Sun Ying. Stress and Deformation of Filament-Wound Thick-Wall Cylinder Pressure Vessels[J]. Journal of Solid Rocket Technology, 2009, 32(6): 680-689 (in Chinese)

[3] Menshykova M, Guz I A. Stress Analysis of Layered Thick-Walled Composite Pipes Subjected To Bending Loading[J]. International Journal of Mechanical Sciences,2014,88:289-299

[4] Zu Lei, Wang Jihui, Li Shuxin. Analysis of Multi-Layered Thick-Walled Filament Wound Hydrogen Storage Vessels[J]. International Journal of Hydrogen Energy, 2014, 39: 21083-21096

[5] Xing Jingzhong, Geng Pei, Yang Tao. Stress and Deformation of Multiple Winding Angle Hybrid Filament-Wound Thick Cylinder under Axial Loading and Internal And External Pressure[J]. Composite Structures,2015,131:868-877

[6] 劉成旭,邢靜忠,陳利,等. 柔性厚壁筒環向纏繞張力分析與設計[J]. 固體火箭技術,2013,36(2):261-265 Liu Chengxu, Xing Jingzhong, Chen Li, et al. Analysis of Residual Winding Tension and Design of Winding Tension for Loop Winding on Flexible Cylinder[J]. Journal of Solid Rocket Technology,2013,36(2):261-265 (in Chinese)

[7] 梁清波,邢靜忠,楊濤. 柱形纏繞件的環向纏繞張力設計的理論研究及其數值模擬[J]. 固體火箭技術,2013,36(6):799-835 Liang Qingbo, Xing Jingzhong, Yang Tao. Theoretical Research And Numerical Simulation of Winding Tension Design of Hoop Winding on Cylindrical Mandrel[J]. Journal of Solid Rocket Technology,2013,36(6):799-835 (in Chinese)

[8] 邢靜忠,梁清波,劉成旭,等. 圓柱形厚壁纏繞件的環向纏繞張力分析的逐層疊加法[J]. 固體火箭技術,2015,38(2): 261-272 Xing Jingzhong, Liang Qingbo, Liu Chengxu, et al. Analysis of Winding Tension for Hoop Winding on Deformable Thick-Walled Cylinder with Superposition by Layers[J]. Journal of Solid Rocket Technology,2015,38(2):261-272 (in Chinese)

[9] 胡勇,許學三,胡吉全. 基于MATLAB的雙折線式多層纏繞卷筒的受力分析研究[J]. 武漢理工大學學報(交通科學與工程版),2015,39(2):297-300 Hu Yong, Xu Xuesan, Hu Jiquan. Force Analysis of Lebus Drum Wound by Multi-Layer Wire Rope Based on MATLAB[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering),2015,39(2):297-300 (in Chinese)

[10] 馬成舉,任立勇,唐峰,等. 基于分布式光纖Bragg光柵傳感技術的光纜卷盤靜態壓力研究[J]. 物理學報,2012,61(5):1-6 Mu Chengju, Ren Liyong, Tang Feng, et al. Study on Static Pressure of Fiber Cable Spool Based on Distributed Fiber Bragg Grating Sensing Technology[J]. Acta Physica Sinica,2012,61(5): 1-6 (in Chinese)

[11] S.鐵摩辛柯,S. 沃諾斯基.板殼理論[M]. 北京:科學出版社,1977:55 S.Timoshenko, S. Woinowsky-Krieger. Theory of Plates and Shells[M]. Beijing, Science Press,1977:55 (in Chinese)

Winding Mechanical Modeling and Simulation of Fiber Optic Cable Spool for Underwater Communication

Tang Weijiang1,2, Liu Weidong1,3, Chen Gang2, Yang Heran2, Zhang Jianjun1

1.School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China 2.The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710077, China 3. Science and Technology on Underwater Information and Control Laboratory,Northwestern Polytechnical University, Xi′an 710072, China

Underwater high-capacity and long-distance communication relies on fiber optic cable and other wired communication methods, because electromagnetic wave can′t propagate in water. Thus, optimizing the design of winding technology and winding mechanism is very important for reducing the probability of communication failure and improving the reliability of underwater communication, especially in the field of underwater vehicles, which releasing the fiber optic cable during the movement of vehicles. A layer-by-layer analysis method which adopts the radial deformation and axial deformation of each cable layer as increments is proposed, and a winding mechanical model of fiber optic cable spool is established on the basis of the mechanical analysis of the cable winding process and the end plate. The model reveals the inherent law of inner tension distribution and end-plate deformation in winding process. The simulations of inner strain and layer pressure and end-plate deformation are carried out, which adopt the parameters of spool structure and winding technology. It is shown that the simulation results of inner strain are consistent with experimental data through comparative analyses.

underwater vehicle, fiber optic cable spool, winding mechanical model, cable axial strain, end-plate deformation

2016-04-18

國家自然科學基金(61473224)資助

湯偉江(1979—)，西北工業大學博士研究生，主要從事水下有線通信技術研究。

TN91

A

1000-2758(2016)06-0996-08