基于二次柵格劃分的移動sink最小路徑構建算法

王薇, 史浩山, 黃鵬宇, 高寶建, 牛進平, 王舉

1.西北工業大學 電子信息學院, 陜西 西安 710072; 2.西北大學 信息科學與技術學院, 陜西 西安 710069 3.西安電子科技大學 通信工程學院, 陜西 西安 710071

基于二次柵格劃分的移動sink最小路徑構建算法

王薇1,2, 史浩山1, 黃鵬宇3, 高寶建2, 牛進平2, 王舉2

1.西北工業大學 電子信息學院, 陜西 西安 710072; 2.西北大學 信息科學與技術學院, 陜西 西安 710069 3.西安電子科技大學 通信工程學院, 陜西 西安 710071

在無線傳感器網絡中引入移動sink能夠有效解決能量空洞問題,從而提高無線傳感器網絡的生存時間。但是移動sink的移動速度限制通常會影響數據收集的時延特性,文章的研究重點即如何為移動sink構建最佳巡航路徑,從而減小信息收集時延。充分利用傳感器節點的通信范圍,將構建最佳路徑問題轉化為求解帶鄰域的旅行商問題TSPN(traveling salesman problem with neighborhoods),并提出了一種基于二次柵格劃分的可變長編碼單親遺傳算法的最佳路徑構建方法。該算法首先在網絡區域中使用粗粒度柵格進行劃分,并利用可變長度編碼的單親遺傳算法獲得最佳途經柵格,從而構造出初始最佳路徑。然后對于每一個途經柵格再次使用細粒度柵格進行劃分以優化收集路徑。仿真結果表明,新算法能夠獲得更短的數據收集路徑,大幅度減低了網絡信息收集時延,有效地拓展了網絡的生存時間。

無線傳感器網絡;移動sink;TSPN;柵格;最短路徑

近年來無線傳感器網絡WSN(wireless sensor network)在環境監測、火情監測、戰場探察等方面得到了廣泛的應用[1]。在這些網絡中,大量的感知節點被部署到被測區域中,每當有敏感事件發生時,傳感器節點將收集到的數據經由多跳路徑傳輸給靜止的匯聚節點(sink節點)。由于全網收集的信息都要逐漸中轉、匯聚,因此必然會導致靠近sink節點的普通節點需要承載更多傳輸負荷,從而消耗更多的能量,最終加速其死亡,并縮短了整個網絡的生存時間,這就是所謂的“能量空洞”問題[2]。

在本項目組所承擔的野生金絲猴相關研究課題中,我們也發現了“能量空洞”問題的存在。我們將大量的無線傳感器節點部署在金絲猴經常出現的區域,由于野外地形所限,sink節點的數量有限,因此其余節點的數據都需要經過多次中轉后到達sink節點。運行一段時間之后,我們發現靠近sink節點的普通節點總是最先耗盡電池。但是由于地處野外,節點電池難以更換,因此非常需要相應的方法來解決能量空洞問題。

近年來,移動sink的概念應運而生,利用移動sink可以優化數據的采集過程,并延長整個網絡的生存時間[3-5],也可利用移動sink來輔助節點定位,由此顯著提高定位精度[6-7]。在以上的研究中,我們可以看到由于移動節點收集信息時更貼近傳感器節點,因此更利于提高信息收集的數量與質量,很好地解決sink固定時節點間耗能均衡的問題。

但是在實際的應用環境中,WSN布設范圍通常較大,而受數據傳輸和承載平臺的限制，移動sink的移動速度大多不高,因此與靜止sink節點相比較,移動sink常常需要更多的時間才能完成全網數據的收集工作。而信息收集時延的大小在實際應用中是一個非常重要的性能衡量指標,因此有必要深入研究移動sink的移動路徑規劃問題,從而盡可能減少數據包的延遲。本文研究的重點即如何為移動sink設計最短的行進路由,從而獲得最小的數據采集時延。

1 相關工作

在收集WSN中的數據時,移動sink通常需要在網絡中按照某種路徑往復運行。在移動過程中,為了節省能量移動sink通常僅會在某些信息匯聚點RP(rendezvous points)上才會開機采集數據,而在運動過程中關閉傳輸電路以節省能量。當移動sink移動到信息收集點時,如果傳感器節點位于移動sink的通信范圍之內,則上傳其相關信息。

按照移動sink是否采用傳感器節點的自身位置作為信息收集點,我們可以將移動sink信息收集方式分為2種類型:①使用傳感器節點位置作為信息收集點坐標的方法,在這類方法中將移動sink的路徑規劃歸結為TSP(travelling salesman problem)問題,見文獻[8-12];②不使用傳感器節點位置作為信息收集點坐標的算法,此時可以將問題歸結為TSP的一種變形——TSPN問題,見文獻[13]。

基于第一種思路,文獻[8]研究了在WSN節點隨機分布的情況下,移動sink的移動速度與信息收集效率之間的關系,并提出了一種MASP(maximum amount shortest path)算法。該算法將時延受限的信息收集問題轉化為一個整數線性規劃問題,并使用遺傳算法以及一種分布式近似算法確定路徑最優解。文獻[9]將數據收集路徑長度最小化問題歸結為一個單跳數據收集問題SHDGP(single-hop data gathering problem)。并將SHDGP問題轉化為一個混合的整數規劃問題進行求解。文獻[10]以滿足時延要求和最小化網絡整體能耗為優化目標,提出了一種基于虛擬點優先級的移動sink路徑優化選擇方法。該方法在犧牲少量能耗的前提下能顯著降低算法時間復雜度。文獻[11-12]則提出了一種基于信息匯聚點RP的移動sink數據收集機制。在該機制中傳感器節點將采集的信息以多跳方式發送給距離最近的RP節點,移動sink依次訪問各PR節點以收集數據。根據第二種思路,文獻[13]將移動sink最短信息收集路徑問題看作是一種帶鄰近區域的旅行商問題TSPN,提出了一種啟發式算法構建信息收集路徑,利用TSP路徑為不自交環路的特征構建賽道,通過內圈啟發式、彎道啟發式以及捷徑搜索尋找賽道內的近似最短路徑。

對于以TSP問題為核心的算法,由于移動sink直接遍歷各個傳感器節點,因此不必考慮節點的通信范圍,從而簡化信息收集問題。但是由于這種方法需要遍歷所有的節點,因此即使感知區域不變,當傳感器節點數量增多時移動sink的信息收集路徑長度也會相應增多,從而導致網絡信息收集時延也隨之增大,所以這一方法在擴展性和實用性方面都存在問題。

相較于基于TSP的方法,采用以TSPN為核心的方法是一個較好的思路。在這類算法中,移動sink并不直接遍歷傳感器節點的位置坐標,而是首先確定一些信息收集點IGP(information gathering position)。這些信息收集點并不僅限于節點的位置,而有可能是部署區域中的任意位置點。移動sink在工作的過程中并不連續收集信息,而是移動到信息收集點的時候才激活以該點為中心的通信范圍內的傳感器節點完成信息收集任務。同時,由于不需要限制IGP的選擇范圍,構建信息收集路徑的將會更加靈活,因此可以在很大程度上縮短信息收集路徑的長度。并且由于不需要簇頭中轉、匯聚信息,所以有更好的能耗表現。但是基于TSPN方法的難點在于如何構建最佳的信息收集路徑。

根據以上分析,本文中我們提出了一種新穎的算法來解決移動sink路徑規劃問題。該算法采用二級柵格劃分的方法對收集點位置進行逐層篩選以減少路徑搜索的空間復雜度,并采用可變長編碼的退火單親遺傳算法計算收集點的最佳遍歷路徑。仿真結果顯示本文算法能夠獲得更短的信息收集路徑長度,可顯著減小移動sink信息收集時延。

2 基于二級柵格劃分的可變長編碼單親遺傳算法

由于基于TSPN的移動sink的最佳信息收集路徑問題的關鍵在于如何選取信息收集點以及如何構建一條最短信息收集路徑。所以,本文所研究的問題可以歸納為:在給定傳感器網絡節點分布的條件下,選擇合適的信息收集點,并確定一條最短的信息收集路徑,依次遍歷所有信息收集點收集信息,最終使信息收集過程的時延最小。

2.1 算法設計

本文算法可以分為2個步驟:

步驟1 為了獲得最佳信息收集路徑,我們首先使用一個較大間隔的柵格將仿真區域劃分為若干柵格單元,并以每個柵格的中心點作為備選的信息收集點,然后在這些備選的收集點集合中使用可變長編碼單親遺傳算法構建一條能夠覆蓋所有節點的最短的信息收集路徑。

在這個過程中,由于節點分布的不均勻性,因此構建的路徑不一定包含所有的備選收集點。我們僅需要在備選收集點集合中找出一個子集,在該子集上收集信息就可以覆蓋網絡中所有節點。這個問題是一個典型的集合覆蓋問題SCP(set cover problem),SCP問題同樣是一個NP-hard問題。而且由于這種覆蓋集所涵蓋的備選信息收集點數目是可變的,所以如果使用遺傳算法構建最佳路徑,則無法使用經典的固定長度編碼方式來表示遍歷路徑的位置序列,所以在這里我們無法使用常規的遺傳算法進行求解。本文中我們使用可變長度編碼的方法來解決這個問題,并對常規的單親遺傳算法進行修改以適應可變長度編碼的問題。

步驟2 通過步驟1我們獲得了第一級最佳路徑。但由于其中所使用的柵格的劃分間隔比較大,所以第一級最佳路徑只是最佳路徑的一個初步結果。為了進一步獲得更精確的遍歷路徑,我們再次針對步驟1中所獲最佳路徑對應的一級柵格再做一次細粒度的柵格劃分。在更細的柵格劃分的基礎上進一步確定收集點的精確位置坐標。在步驟2中由于在每一個一級柵格中還是選取一個收集點位置,所以在該過程中收集點的數量是固定不變的,且與一級最佳路徑中涉及的柵格數相同。因此,為了提高運算速度,在這里我們使用固定長度編碼的單親遺傳算法進行計算。最終就可以獲得更加精確的二級最佳信息收集路徑,并將其作為我們算法的最終結果。

圖1 二級柵格劃分方法

通過這種二級柵格篩選方法可以有效簡化信息收集點的選擇,降低算法的計算量,為之后最佳路徑計算創造了有利條件。

2.2 算法流程

i∈I,j∈J,l∈N}

式中,nodel表示第l個傳感器節點的位置坐標,I、J分別表示橫、縱軸劃分的柵格數,N表示場景中的節點數,“‖‖”表示進行歐氏距離計算。

算法流程描述如下:

Step1 產生初始種群

Step2 計算適應值

適應值是遺傳算法的進化依據,在本文算法中,選擇個體對應路徑長度作為個體的適應值,適應值越小代表個體越優秀。

Step3 運行可變長度編碼單親遺傳算法

為了保持進化過程中個體長度的可變特性,本文設計了2個算子:倒序算子和置換算子。

倒序算子:對于一個個體,根據個體長度隨機選擇倒序的起始、終結位置t1,t2,不失一般性設t1≤t2,然后將t1→t2的路徑倒置為t2→t1的路徑。

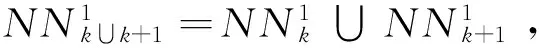
Step4 最優保持策略

在算法的運行過程中,將每一代中的最優個體保存下來;在倒序、置換操作完成后,比較上一代的最優個體值與當代最優個體值;若當代最優個體較差,則使用上代最優個體替換當代最差個體。

Step5 退出條件判斷。

Step6 二次柵格劃分及求解

在通過粗粒度柵格劃分大致確定最佳信息收集路徑之后,為了獲得更加精確的信息收集路徑,從而進一步減少信息收集時延,我們對所獲得的一級最佳路徑所涉及的一級柵格再次使用更小粒度的柵格進行劃分,并且在每一個粗粒度柵格中只選擇一個細粒度柵格中心作為路徑的信息收集點備選位置。通過這一過程,整個路徑的進一步構建就轉化為對每個粗粒度柵格中細粒度柵格中心的選擇過程,由于此時粗粒度柵格的數目已經固定,所以這里的搜索問題就變成一個固定IGP數量的路徑優化問題,即信息收集路徑上的信息收集點的數目是固定的。因此,我們在這里就可以采用定長編碼的單親遺傳算法來加以解決,最終可以獲得一條更好、更短的信息收集路徑。

3 仿真結果分析

我們對文中所提出的算法進行了仿真,并將仿真結果與基于TSP的方法以及一種基于TSPN思路的算法——COM算法[14]進行對比分析,為方便起見,我們將本文所提出的算法簡稱為TGDA。

為了對比方便,本文采用和文獻[14]相同的仿真設置。仿真中傳感器節點均勻分布在在500 m×500 m的矩形區域里;節點數50～100個節點;傳感器節點與移動sink節點具有相同的通信半徑,半徑設置為20～100 m;每次生成50個拓撲,每一個拓撲仿真50次。

為了更加清晰地體現算法性能,首先我們固定節點的通信半徑為50 m和100 m,節點數由50逐級增加到100,并在這一過程中對3個算法的性能進行仿真,結果如圖2所示。然后我們將節點數固定為50和100,節點的通信半徑從20 m逐漸增加到100 m,再次對3個算法進行仿真,獲得的結果顯示如圖3所示。

圖2 節點通信半徑固定時TGDA算法的性能 圖3 節點數固定時TGDA算法的性能

從圖2的仿真結果可以看出,在通信半徑固定的情況下,無論網絡中的節點數為50還是100,3種算法所獲得的最佳路徑長度都在逐漸增加。這是因為隨著節點數的增多,移動sink需要經歷的節點數也會同步增長,所以路徑長度會隨之增加。在節點數的不同設置下,顯而易見TSP算法的性能都是最差的。這是由于在TSP算法中,每個傳感器節點的位置就是IGP的位置,因此移動sink需要遍歷所有節點位置才能完成信息收集任務,因此該算法所獲得的路徑長度必然是其中最長的。相較于TSP算法,COM算法的性能有了不小的提高。由于COM算法會根據相鄰IGP覆蓋范圍的重疊程度選擇合并相鄰的IGP,這樣COM算法生成的路徑中包含的IGP更少,所以生成的路徑長度相對更好。相較于對比算法本文提出的TGDA算法具有最好的算法性能,在通信半徑50m、節點數50的情況下TGDA算法生成的路徑長度比COM算法縮短了33.37%。若節點數增加為100,TGDA算法的優勢更是擴大到了35.19%。

在固定節點數為50和100,節點通信半徑由20 m增加到100 m時,仿真結果同樣相似。在固定節點數時可以看到由于TSP算法遍歷所有的節點位置,因此在節點數不變的情況下TSP算法的性能基本沒有變化。隨著節點通信半徑的增加,由于COM和TGDA算法都考慮到節點的通信范圍能力,因此這2種算法的性能都有了相應提高。并且節點通信半徑越大意味著移動sink節點可以在更大的范圍內收集到節點上傳信息。所以隨著通信半徑的增長,COM以及TGDA算法的性能提高程度都隨之擴大,但本文算法提高程度更高。從圖3中看到,在節點數為50、通信半徑為100 m時,相較于COM算法TGDA算法的路徑長度減少了43.51%,若節點數增加到100,TGA算法的優勢擴大到48.16%。

以上仿真結果可見在不同的仿真配置下,本文提出的TGDA算法都取得了優異的結果。TGDA算法能有效減少了移動sink的信息收集路徑長度,從而降低了移動sink系統的信息收集時延,進而提高了整個系統的執行效率。

4 結 論

信息收集是WSN的一個關鍵應用領域,是WSN實際應用的基礎。移動sink的引入使sink節點只需要通過傳感器節點通信范圍即可完成節點信息的收集,減少了信息傳輸的環節,簡化了網絡協議的復雜度。本文在充分考慮節點的無線通信特性的條件下,研究了移動sink在WSN中的最佳信息收集路徑規劃問題。在移動sink最佳信息收集路徑的搜索過程中,本文算法通過二次柵格劃分的方法來篩選信息收集點的搜索范圍,簡化算法的計算復雜度,在路徑構建過程中的提出了一種新穎的基于可變長編碼的單親遺傳算法來進行路徑搜索。仿真結果表明本文算法與傳統的基于TSP的算法相比,能夠獲得更好(短)的信息收集路徑,減少了傳感器節點的傳輸能耗、延長了網絡的生存時間。與基于TSPN的算法相比本文算法原理簡單,擴展性好,能夠獲得更好的信息收集路徑。因此本文算法非常適用于大規模WSN網絡信息收集路徑的構建應用。

[1] Ou C H. A Localization Scheme for Wireless Sensor Networks Using Mobile Anchors With Directional Antennas[J]. IEEE Sensors Journal, 2011, 11(7):1607-1616

[2] Olariu S, Stojmenovi I. Design Guidelines for Maximizing Lifetimeand Avoiding Energy Holes in Sensor Networks with Uniform Distribution and Uniform Reporting[C]∥IEEE Infocom, 2006: 1-12

[3] Zhao M, Yang Y. Bounded Relay Hop Mobile Data Gathering in Wireless Sensor Networks[J]. IEEE Trans on Computers, 2012, 61(2): 265-277

[4] Lin K, Chen M, Zeadally S, et al. Balancing Energy Consumption with Mobile Agents in Wireless Sensor Networks[J]. Future Generation Computer Systems, 2012, 28(2): 446-456

[5] Guo S, Wang C, Yang Y. Joint Mobile Data Gathering and Energy Provisioning in Wireless Rechargeable Sensor Networks[J]. IEEE Trans on Mobile Computing, 2014, 13(12): 2836-2852

[6] Liao W H, Lee Y C, Kedia S P. Mobile Anchor Positioning for Wireless Sensor Networks[J]. IET Communications, 2011, 5(7):914-921

[7] Chen H, Shi Q, Tan R, et al. Mobile Element Assisted Cooperative Localization for Wireless Sensor Networks with Obstacles[J]. IEEE Trans on Wireless Communications, 2010, 9(3): 956-963

[8] Gao S, Zhang H, Das S K. Efficient Data Collection in Wireless Sensor Networks with Path-Constrained Mobile Sinks[J]. IEEE Trans on Mobile Computing, 2010, 10(4): 592-608

[9] Ma M, Yang Y, Zhao M. Tour Planning for Mobile Data-Gathering Mechanisms in Wireless Sensor Networks[J]. IEEE Trans on Vehicular Technology, 2013, 62(4):1472-1483

[10] 郜帥, 張宏科. 時延受限傳感器網絡移動Sink路徑選擇方法研究[J]. 電子學報, 2011, 39(4):742-747 Gao Shuai, Zhang Hongke. Optimal Path Selection for Mobile Sink in Delay-guaranteed[J]. Acta Electronica Sinica, 2011, 39(4):742-747 (in Chinese)

[11] Xing G, Wang T, Jia W, et al. Rendezvous Design Algorithms for Wireless Sensor Networks with a Mobile Base Station[C]∥ACM International Symposium on Mobile Ad Hoc Networking and Computing, 2008: 231-240

[12] Xing G, Wang T, Xie Z, et al. Rendezvous Planning in Wireless Sensor Networks with Mobile Elements[J]. IEEE Trans on Mobile Computing, 2008, 7(12):1430-1443

[13] 袁遠, 彭宇行, 李姍姍,等. 高效的移動sink路由問題的啟發式算法[J]. 通信學報, 2011, 32(10):107-117 Yuan Yuan, Peng Yuxing, Li Shanshan, et al. Efficient Heuristic Algorithm for the Mobile Sink Routing Problem[J]. Journal on Communications, 2011, 32(10):107-117 (in Chinese)

[14] He L, Pan J, Xu J. A Progressive Approach to Reducing Data Collection Latency in Wireless Sensor Networks with Mobile Elements[J]. IEEE Trans on Mobile Computing, 2013, 12(7):1308-1320

A Routing Planning Algorithm base on Twice Grid Division for Mobile Sink

Wang Wei1,2, Shi Haoshan1, Huang Pengyu3,Gao Baojian2, Niu Jinping2, Wang Ju2

1.School of Electronics and Information, Northwestern Polytechnical University, Xi′an 710072, China 2. School of Information and Technology, Northwest University, Xi′an 710069, China 3. School of Telecommunications Engineering, Xidian University, Xi′an 710071, China

Introduce mobile sinks into wireless sensor networks can balance the energy level of the sensor nodes, resolve the hotspot problem and prolong the lifetime of the whole network. However, the mobility of the sink may also introduce additional delays. Therefore, it is important to design an efficient routing protocol for the mobile sink. In this paper, we deduce this routing planning problem into a Traveling Salesman Problem with Neighborhoods (TSPN). In addition, we propose a routing design algorithm base on twice grid division and variable-length Partheno-genetic Algorithm. In this algorithm, we divide the network area with the grids coarse-grained, and obtain the grids on the best path with variable-length Partheno-genetic Algorithm. We then divide every grid on the path with the grids fine-grained in order to optimize the path. Finally, we implement this algorithm in Matlab and the simulation results show that the proposed algorithm can significantly improves the efficiency and effectiveness of the routing planning for the mobile sink.

wireless sensor network; mobile sink; TSPN; routing planning; grid division

2016-04-12 基金項目：國家自然科學基金(61170218、61602379)與陜西省教育廳自然科學基金(15JK1742、12JK0937)資助

王薇(1977—)，女，西北工業大學博士研究生，西北大學講師，主要從事信息網絡理論、無線傳感器網絡研究。

TP393

A

1000-2758(2016)06-1016-06