基于PPCA修正模型的HRRP穩健識別方法

李彬, 李輝, 黃偉斌

(西北工業大學 電子信息學院, 陜西 西安 710129)

基于PPCA修正模型的HRRP穩健識別方法

李彬, 李輝, 黃偉斌

(西北工業大學 電子信息學院, 陜西 西安 710129)

高信噪比情況下，利用概率主成分分析(PPCA,probabilistic principal component analysis)模型識別雷達高分辨距離像(HRRP,high resolution range profile)取得了較高的識別率。但在實際工作環境中，測試階段獲取的HRRP常為低信噪比樣本，由此造成的模型失配問題極大影響了識別性能。為此文章利用不同噪聲來源造成的模型失配先驗信息，在模型空間針對不同信噪比的測試樣本補償PPCA模型參數，以達到穩健識別的目的。另一方面，利用2種方法通過直接估計測試樣本的噪聲功率省去最優化計算的步驟，避免了求解最優補償參數時需要大量計算的問題，提高了識別效率。最后，利用最大后驗概率確定目標所屬類別，證明了2種方法在信噪比低于20 dB時的可行性。

雷達目標識別；飛機目標探測；脈沖重復頻率；高分辨距離像；概率主成分分析；模型修正

基于HRRP的目標識別一直是雷達目標識別的熱門領域[1]，且一般都遵循預處理、特征提取選擇、分類識別的處理流程。

HRRP的統計特征能夠反映其幅度起伏特性，因此在特征提取階段，對HRRP進行統計建模將建模問題轉換為模型選擇和參數估計問題[2]，能夠獲取可分性更高、更有價值的特征。文獻[3]指出HRRP在PPCA和FA模型下近似服從聯合高斯分布，提升了參數估計的效率。文獻[4]在PPCA模型的基礎上，利用EM算法和KL距離對HRRP重新分幀，提升了大范圍方位角內HRRP的識別率。

但實際工作環境中，獲取的HRRP回波由于受到目標遠近、雜波和天氣等因素的影響具有相對較低的信噪比，如果直接應用高信噪比環境中估計的PPCA模型參數會造成模型失配，影響識別性能[5]，這也是基于統計建模面臨的普遍問題。為此相關文獻從造成模型失配的原因入手，做了許多工作。文獻[6]對FA模型進行非參數化修正并預先估計噪聲水平，提升了小樣本情況下FA模型的穩健性。文獻[7]在假設HRRP各距離單元噪聲服從復高斯分布的基礎上，補償不同信噪比下統計模型的參數。文獻[8]利用參數尋優將基本PPCA修正為對噪聲穩健的自適應PPCA模型。本文引入訓練樣本與測試樣本模型匹配度的概念，利用噪聲與信號的向量關系，得到針對不同信噪比測試樣本的PPCA修正模型，增強了PPCA模型在不同信噪比環境下的穩健性。

1 模型修正和概率主成分分析

1.1 模型修正

雷達識別系統工作的典型模式是高信噪比下訓練，低信噪比下識別。這使得應用PPCA模型時，不得不考慮模型在訓練樣本與測試樣本之間的匹配問題。

從圖1看出，由于受到噪聲的影響，獲取的PPCA模型參數ΛX={μX,WX,σX}和ΛY={μY,WY,σY}并不相同,如果使用訓練樣本模型ΛX,通過最大后驗概率判定測試目標則必然造成識別率的下降。根據引起模型差異的原因,通過構造差異函數D1(·)、D2(·)和D3(·)消除模型間的失配,達到穩健識別的目的。

圖1 訓練階段與測試階段的信息不匹配

對于HRRP識別系統,假設訓練數據集為X={x1,x2,…,xn},測試數據集為Y={y1,y2,…,yn}。在特征空間內,通過構造從測試數據集到訓練數據集的映射X=Fv(Y),或在模型空間構造映射ΛY=Gη(ΛX),消除噪聲的影響。可得

(1)

(2)

1.2 概率主成分分析模型

隱變量參數模型是PPCA模型的基礎[9]

y=Wx+μ+ε

(3)

等式(3)中,隱變量x服從獨立高斯分布N(0,I)。ε為觀測噪聲向量,服從N(0,ψ)。觀測向量y服從N(μ,WWT+ψ)。得到模型參數為{μ,W,σ},可通過最大似然估計或期望最大值算法得到具體參數:

(4)

(5)

(6)

2 基于修正模型的穩健識別

修正PPCA模型的目的是對高信噪比條件下的模型參數進行補償,以便準確反映不同信噪比下測試樣本的分布。但是求解補償參數是一個極值搜索問題,必然造成大量的計算。通過分析可知,不同信噪比下的PPCA補償參數與疊加的噪聲功率直接相關。如果能尋找一種估計測試樣本噪聲功率的方法,就可以避免求解最優化問題,降低系統的計算負擔。

2.1 基于復高斯噪聲的參數修正

HRRP是對采樣后的復距離像取模得到的,即x=[|x(1)|,|x(2)|,…,|x(N)|]T。噪聲n疊加在復數域,則任意一個距離單元內的復信號模型可表示為|x|=|s+n|。如果定義高信噪比的HRRP為|xh|,則低信噪比的HRRP為|xl|:

|xl|=|xh+n|=

(7)

(8)

噪聲與信號間的夾角θ∈[0,π],概率密度函數為:

p(θ)=1/π

(9)

利用隱函數關系f(|xl|2,wvcosθ)=0求解|xl|的密度函數p(|xl|)。令W=|xh|,v=|n|則各變量的聯合密度函數為p(W2,V2,wvcosθ),首先計算cosθ的概率密度函數:

(10)

假設Z=XY,已知X,Y的聯合概率密度函數f(x,y),根據(11)式計算Z的密度函數:

(11)

利用(11)式的結果計算(w,v,cosθ)的聯合概率密度函數p(w,v,cosθ):

(12)

(13)

得到|xl|的概率密度函數p(|xl|):

(14)

(14)式過于復雜,修正模型意義不大。計算|xl|的近似分布。已知信號與噪聲獨立,期望E(|xh||n|cosθ)=0。(7)式可簡化:

(15)

計算u=|xh|2和v=|n|2的概率密度函數:

(16)

(17)

由于|xh|2和|n|2獨立,按照隨機變量和的分布計算規則,計算z=|xl|2的密度函數:

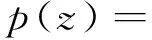
(18)

進而得到|xl|的概率密度函數p(|xl|):

(19)

按不發生越距離單元徙動的角度為標準,將c個目標的訓練HRRP劃分為m幀模板。則對任意一組測試HRRP,其關于第c個目標第m幀HRRP模板的輔助函數可表示為:

(20)

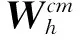
(21)

可得針對第c個目標第m幀HRRP的PPCA模型的均值修正值μ0為:

(22)

通過輔助函數f(|xl|)cm計算第c個目標第m幀HRRP的PPCA模型噪聲協方差輔助矩陣φcm:

(23)

(24)

2.2 基于高斯噪聲的參數修正

(25)

從(25)式可知，低信噪比條件下，HRRP幅度仍服從高斯分布。

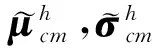
(26)

(27)

(28)

(29)

2.3 測試樣本噪聲功率的確定

中值濾波估計器常用來估計不同測試樣本的噪聲水平[11]。對于一個待測信號xn=x+n,n表示疊加的噪聲,首先去除原始信號x的影響:

(30)

運算符?表示卷積,fdi表示i階有限沖激響應高通濾波器。則近似的噪聲信號為:

(31)

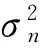
(32)

對于實HRRP信號xl,其在高斯模型下的噪聲方差δ2為:

(33)

將等式(32)、(33)帶入等式(22)、(24)、(28)和(29)中,得到針對不同信噪比條件下,測試HRRP的PPCA修正模型參數。

3 仿真實驗

識別實驗使用的HRRP數據按照文獻[12]所示方法獲取,包括4類飛機外形的目標A、B、C、D。采用步進頻雷達,步進頻2 MHz,脈沖重復頻率4 KHz,步進數200,對應的HRRP距離分辨率為0.375 m,包含400個距離單元。設置4類目標的方位角變化范圍為0-180°,每隔0.1°取一次回波數據作為訓練樣本。重新設置不同的偏航角,俯仰角和橫滾角,每步進0.05°取1次回波數據作為測試樣本。根據目標的橫向尺寸(近似為10 m),以不發生越距離單元徙動的角度δ(MTRC)=4°,劃分角域。

PPCA模型描述HRRP各個分幀的統計分布,準確性受隱變量維數q的影響。當q較低時,PPCA模型不足以描述HRRP的真實數據結構;另一方面PPCA自由參數的數量為dq+1-q(q-1)/2,當隱變量維數較多時,需要估計的參數增多,對于訓練樣本有限的情況,估計的精度會有所下降。針對訓練樣本和測試樣本均為高信噪比的情況,以最大后驗概率分類器檢驗識別結果。通過PPCA建模獲取c個目標第m幀的統計參數μcm和∑cm,則對測試樣本xtest的判定結果為:

(34)

圖2給出了A、B、C、D類目標識別率隨隱變量維數q變化的曲線,基本反映了PPCA模型描述HRRP分布的性能。

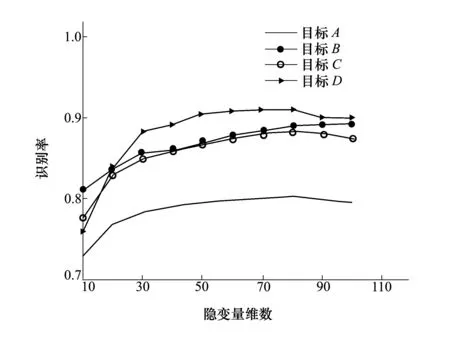
圖2 各目標識別率隨隱變量維數變化的曲線

(35)

高斯噪聲增量下的判別規則:

(36)

圖3給出了PPCA模型，基于高斯噪聲的PPCA修正模型和基于復高斯噪聲的PPCA修正模型在不同噪聲強度下平均識別率的變化情況。

圖3 PPCA模型和2類PPCA修正模型的平均識別率隨信噪比變化的曲線

由圖3可知，將PPCA模型應用于低信噪比測試樣本的識別時，平均識別率非常低。可以這樣認為，當信噪比低于20dB時，PPCA模型其實已經失效。而提出的另外兩種PPCA修正模型卻在低信噪比下有60%左右的平均識別率，明顯的提高了識別性能，削弱了訓練樣本與測試樣本之間的失配現象。而隨著信噪比的提升，PPCA模型的平均識別率才逐步趨近于本文提出的兩種PPCA修正模型。

4 結 論

在實際應用中，雷達目標識別系統獲取的HRRP常處于強噪聲背景中，信噪比較低，極大地影響了測試樣本固有的統計特性，導致由訓練樣本估計的PPCA模型很難適用于測試樣本。本文通過分析低信噪比信號與噪聲的關系，先驗的估計不同噪聲源的功率，得到兩種PPCA修正模型。這兩種修正模型能夠根據測試樣本的噪聲水平，修正模型參數，提高低信噪比環境下測試的穩健性。

[1] 郭尊華,李達,張伯彥,等. 雷達高距離分辨率一維像目標識別[J]. 系統工程與電子技術,2013,35(1):53-60 Guo Zunhua, LI Da, Zhang Boyan, et al. Survey of Radar Target Recognition Using One-Dimensional High Range Resolution Profiles[J]. Systems Engineering and Electronics, 2013, 35(1):53-60 (in Chinese)

[2] Liu H W, Du L, Wang P H, et al. Radar HRRP Automatic Target Recognition: Algorithm and Applications[C]∥IEEE CIE International Conference on Radar, 2011: 14-17

[3] Du L, Liu H W, Bao Z. Radar HRRP Statistical Recognition: Parametric Model and Model Selection[J]. IEEE Trans on Signal Process, 2008, 56(5): 1931-1944

[4] 王鵬輝,杜蘭,劉宏偉,等. 雷達高分辨距離像分幀新方法[J]. 西安電子科技大學學報,2011,38(6):22-29 Wang Penghui, Du Lan, Liu Hongwei, et al. New Frame Segmentation Method for Radar HRRPs[J]. Journal of Xidian University, 2011,38(6): 22-29 (in Chinese)

[5] Liu H W, Chen F, Du L, et al. Robust Radar Automatic Target Recognition Algorithm Based on HRRP Signature[J]. Frontiers of Electrical and Electronic Engineering, 2012,7(1): 49-55

[6] Du L, Liu H W, Wang P H, et al. Noise Robust Radar HRRP Target Recognition Based on Multitask Factor Analysis with Small Training Data Size[J]. IEEE Trans on Signal Processing, 2012, 60(7): 3546-3559

[7] Pan M, Du L, Wang P H, et al. Noise-Robust Modification Method for Gaussian-Based Models with Application to Radar HRRP Recognition[J]. IEEE Geoscience and Remote Sensing Letters, 2013,10(3):558-562

[8] Hou Q Y, Chen F, Liu H W, et al. Adaptive Statistical Model for Radar HRRP Target Recognition[C]∥IET Radar Conference, 2009

[9] Tipping M E, Bishop C M. Mixtures of Principal Component Analyzers[J]. Neural Compute, 1999, 11(2):443-482

[10] Gales M J F, Woodland P C. Mean and Variance Adaptation Within the MLLR Framework[J].Computer Speech & Language, 1996, 10(4): 249-264

[11] Pei Z J, Tong Q Q, Wang L N, et al. A Median Filter Method for Image Noise Variance Estimation[C]∥International Conference on Information Technology and Computer Science, 2010, 13-16

[12] 黃得雙. 高分辨雷達智能信號處理技術[M]. 北京:機械工業出版社, 2001 Huang Deshuang. Intelligent Signal Processing Technique for High Resolution Radars[M]. Beijing, China Machine Press, 2001:19-31 (in Chinese)

Modified PPCA Methods for Radar HRRP Robust Recognition

Li Bin, Li Hui, Huang Weibin

(School of Electronic and Information, Northwestern Polytechnical University, Xi′an 710129, China)

In the condition of high signal-to-noise ratio(SNR), utilizing probabilistic principal component analysis(PPCA) model obtained high recognition rate in radar high resolution range profile (HRRP) recognition field. But in the actual working environment, HRRPs getting from the test phase usually have low SNR which will cause model mismatch problem influencing recognition rate. In order to get noise robust PPCA based methods, according to the prior mismatch information which are caused by different noise sources, the modified PPCA statistic parameters are computed to make up for the error of mismatch in model space. On the other hand, the two methods proposed in this paper directly estimate the increased noise power to avoid the step in solving optimization problem of modified parameters which greatly improve the calculation efficiency. Finally, in the simulation experiment applying the maximum a posteriori probability classifier to test the modified PPCA model, the results show the feasibility of these two methods below 20 dB SNR.

radar target recognition; aircraft detection; pulse repetition rate; high resolution range profile; probabilistic principal component analysis; model modification

2016-09-01

國家自然科學基金(61571364)與西北工業大學研究生創新創意種子基金(Z2016022)資助

李彬(1986—)，西北工業大學博士研究生，主要從事模式識別及雷達數據處理研究。

TN959.1

A

1000-2758(2016)06-1022-06