基于自適應滑模觀測器的五相永磁同步電機無位置傳感器控制

楊劍威, 竇滿峰,趙冬冬, 顏黎明, 方淳

(西北工業大學 自動化學院, 陜西 西安 710072)

基于自適應滑模觀測器的五相永磁同步電機無位置傳感器控制

楊劍威, 竇滿峰,趙冬冬, 顏黎明, 方淳

(西北工業大學 自動化學院, 陜西 西安 710072)

由于三次諧波的影響,三相永磁同步電機的無位置傳感器控制方法無法直接應用于五相永磁同步電機無位置傳感器控制。在考慮三次諧波電壓和電流的條件下,提出一種基于自適應滑模觀測器的五相永磁同步電機無位置傳感器控制方法。該方法首先利用帶三次諧波的五相永磁同步電機模型設計了滑模觀測器,并用sigmoid函數代替一般滑模觀測器常用的符號函數作為觀測器的開關函數,以減小滑模抖動并獲得更為準確的反電勢當量信號。其次設計了反電勢自適應觀測器以估計電機轉速和位置信號,消除了常規無位置傳感器控制系統中所必需的低通濾波器和相位補償單元,提高了轉速和位置信號的估計精度。此外,利用李雅普諾夫準則,證明了所設計的滑模觀測器和反電勢自適應觀測器的穩定性,并利用Matlab/Simulink進行了仿真實驗。仿真結果顯示,與常規滑模觀測器相比,所提出的自適應滑模觀測器在五相永磁同步電機無位置傳感器控制系統中抖動更小,轉速和位置估計誤差更小,反電勢估計更為準確,具有較強的魯棒性。

五相永磁同步電機;無位置傳感器控制;自適應滑模觀測器;李雅普諾夫準則

五相永磁同步電機由于具有較高的效率、功率因數和密度、以及較強的容錯能力,廣泛應用于機床、機器人、電動汽車、風力發電以及航空航天等對功率和可靠性有較高要求的應用場合[1-4]。在五相永磁同步電機驅動控制系統中,常規的磁場定向控制策略需要通過固定在電機轉軸上的光電編碼器等位置傳感器獲得電機的轉速和位置信息,從而實現五相永磁同步電機的閉環控制。然而,常規的位置傳感器對振動條件和溫度條件較為敏感,從而降低了整個電機驅動控制系統的可靠性,并限制了五相永磁同步電機在相對嚴苛環境條件下的應用[5]。

隨著數字信號處理器技術的發展,永磁同步電機無位置傳感器控制技術在電機驅動控制研究領域得到了廣泛關注[6]。永磁同步電機無位置傳感器控制技術主要分為2類：①基于永磁同步電機凸極效應的高頻信號注入法[7]；②基于電機模型的觀測器估計法[8]。高頻信號注入法的缺點之一是,所注入高頻信號帶來的噪聲將導致電機驅動控制系統性能下降。而觀測器估計法中的模型參考自適法[9]和卡爾曼濾波法[10]又較為依賴精確的電機模型。相比之下,滑模觀測器法由于其較強的魯棒性、較為簡單的算法實現以及相對獨立于電機模型,是一種較為有效的電機轉速和轉子位置估計方法,并在三相永磁同步電機無位置傳感器控制系統中得到了廣泛應用。

在永磁同步電動機無位置傳感器驅動控制系統中,滑模觀測器法一般在靜止參考坐標系下,通過滑模觀測器得到定子相電流的估計值,并與電流傳感器采樣得到的定子電流實測值進行比較,得到定子相電流估計誤差,來獲得反電勢當量信號,從而進一步估計電機的轉子轉速和位置。在常規滑模觀測中,一般利用符號函數作為觀測器的開關函數,來獲得反電勢的當量信號。然而,由于符號函數的離散性,常規滑模觀測器中抖振現象嚴重,且反電勢當量信號中包含大量的高頻振蕩分量。因此,在常規滑模觀測法中,往往需要利用低通濾波器對滑模觀測器獲得的反電勢當量信號進行濾波,得到轉速和轉子位置估計所需的反電勢信號。但是,低通濾波器的引入又會造成相位延遲,使得常規滑模觀測器不得不加入相位補償模塊,從而使整個滑模觀測器的結構更加復雜。為了解決這一問題,文獻[11]中提出了一種自適應濾波器方法,但仍無法完全實現相位補償。文獻[12]中為了減小滑模抖振,用飽和函數代替符號函數,作為滑模觀測器的開關函數,然而,由于飽和函數仍然是一種離散函數,因此其滑模抖振現象依然較為明顯。文獻[13]中,摒棄了常規滑模觀測器所使用的符號函數和飽和函數,利用sigmoid函數作為滑模觀測器的控制函數,由于該函數是連續函數,因此滑模抖振明顯減小。文獻[14]設計了一種帶自適應反電勢觀測器的滑模觀測器,消除了常規滑模觀測器中的低通濾波器和相位補償單元,提高了電機轉速和轉子位置估計的精度。然而,文獻[13]和[14]中所提出的滑模觀測器均是關于三相永磁同步電機無位置傳感器驅動控制系統,而對于五相永磁同步電機無位置傳感器驅動控制系統,為了實現較為精確的電機轉速和轉子位置觀測,三次諧波的影響將無法直接忽略,滑模觀測器中的三次諧波電流項必須考慮,且在利用李雅普諾夫準則,對觀測器的穩定性和收斂性進行分析時,三次諧波項也會對觀測器的穩定性和收斂性條件造成影響,使得五相永磁同步電機無位置傳感器驅動控制系統中的滑模觀測器設計更為復雜和困難。

本文在考慮三次諧波電壓和電流的條件下,提出一種基于自適應滑模觀測器的五相永磁同步電機無位置傳感器控制方法。該方法首先利用帶三次諧波的五相永磁同步電機模型設計了滑模觀測器,并用sigmoid函數代替一般滑模觀測器常用的符號函數作為電流觀測器的開關函數,以減小滑模抖動并獲得更為準確的反電勢當量信號。其次設計了反電勢自適應觀測器來估計電機轉速和位置信號,消除了常規無位置傳感器控制系統中滑模觀測器所必需的低通濾波器和相位補償單元,提高了轉速和位置信號的估計精度。此外,利用李雅普諾夫準則,證明了所設計的滑模觀測器和反電勢自適應觀測器的穩定性。

1 無位置傳感器驅動控制系統

基于自適應滑模觀測器的五相永磁同步電機無位置傳感器驅動控制系統原理框圖如圖1所示。系統主要由五相永磁同步電機、電流閉環、轉速閉環、空間矢量脈寬調制單元、坐標變換單元以及自適應滑模觀測器構成。值得注意的是,在五相永磁同步電機無位置傳感器驅動控制系統中,為了實現較為精確的電機轉速和轉子位置觀測,三次諧波的影響無法直接忽略,在觀測和控制基波電流和電壓分量的同時,三次諧波電壓和電流也需要被觀測和控制。

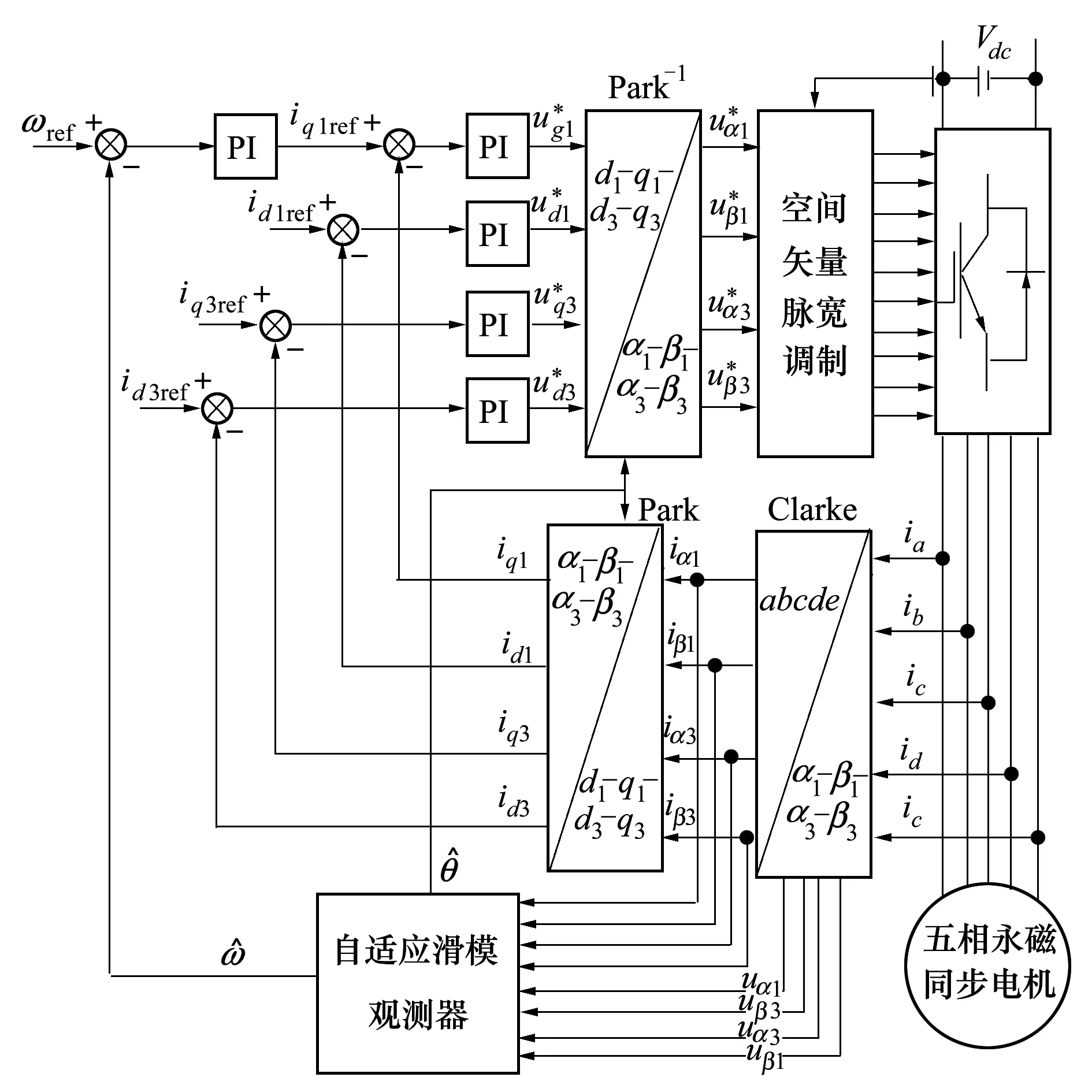
圖1 基于自適應滑模觀測器的五相永磁同步電機無位置傳感器驅動控制系統原理框圖

從圖1可以看出,在五相永磁同步無位置傳感器驅動控制系統中,用于觀測電機轉速和轉子位置的自適應滑模觀測器是實現無位置傳感器控制的核心和基礎。

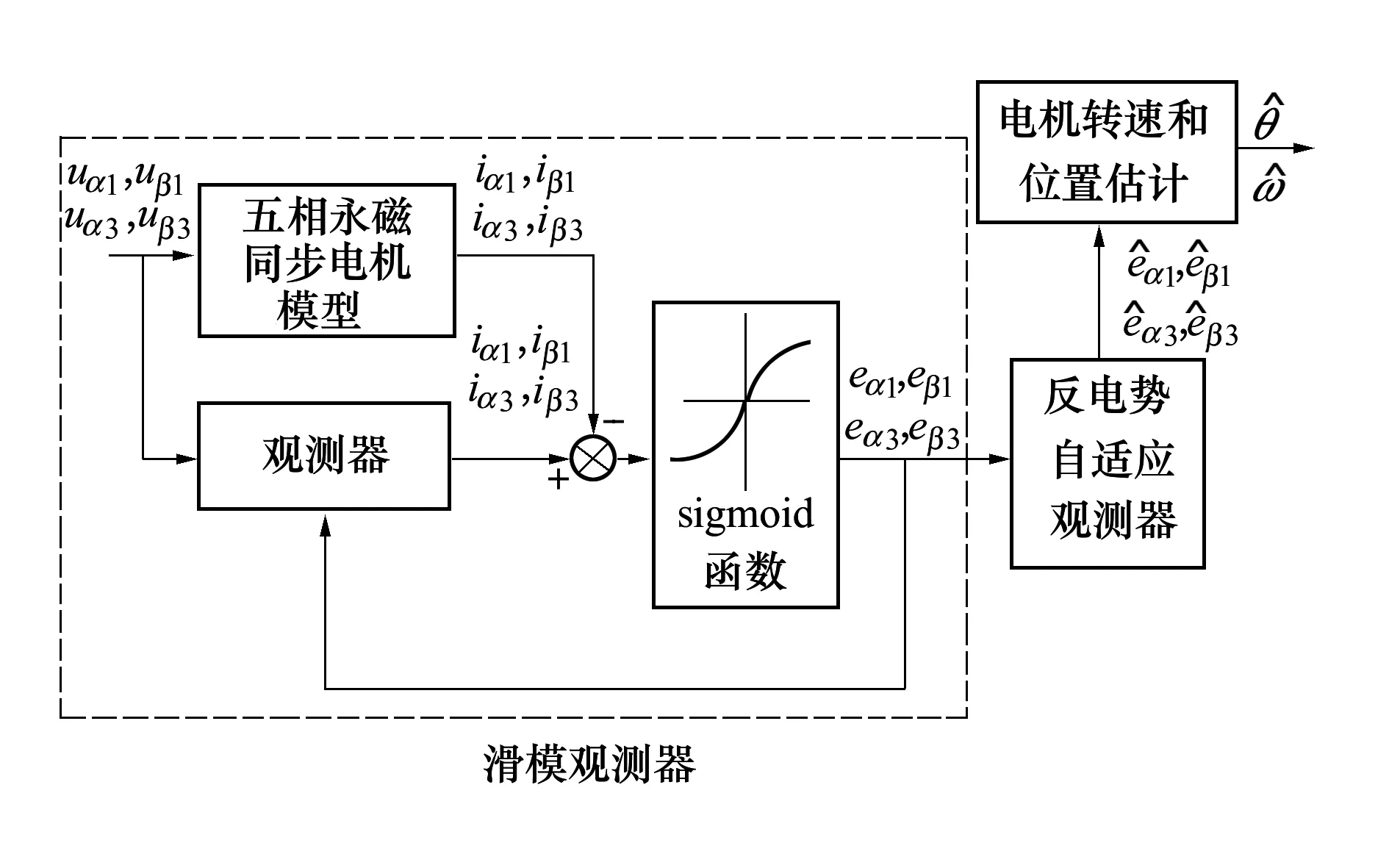
圖2 自適應滑模觀測器原理框圖

圖2是所提出的自適應滑模觀測器的原理框圖。該觀測器主要由滑模觀測器和反電勢自適應觀測器構成,在觀測基波電流的同時還對三次諧波電流進行了觀測。其中滑模觀測器采用sigmoid函數,代替常規滑模觀測器中的符號函數,作為觀測器的開關函數。由于sigmoid函數是一個連續函數,使得整個滑模觀測器的滑模抖動現象明顯減小,同時,在滑模觀測器之后,利用反電勢自適應觀測器來對反電勢信號進行濾波和觀測,實現電機轉速和轉子位置的估計,從而消除了低通濾波器和相位補償模塊,使得整個滑模觀測器的結構相對簡單。

2 自適應滑模觀測器設計

所提出的自適應滑模觀測器主要由滑模觀測器和反電勢自適應觀測器兩部分構成,因此,觀測器設計主要包括滑模觀測器設計和反電勢自適應觀測器設計兩部分。

2.1 滑模觀測器設計

為了構造五相永磁同步電機無位置傳感器驅動控制系統的滑模觀測器,首先需要五相永磁同步電機在靜止坐標系下的模型。考慮三次諧波的影響,五相永磁同步電機靜止坐標系α1-β1-α3-β3下的電壓平衡方程如(1)式所示:

(1)

式中,下標α1、β1表示基波分量;α3、β3表示三次諧波分量;Rs為定子繞組阻值;[uα1uβ1uα3uβ3]T是靜止坐標系α1-β1-α3-β3下的定子電壓矢量;[iα1iβ1iα3iβ3]T是靜止坐標系下的定子電流矢量;對角陣diag(Lα1Lβ1Lα3Lβ3) 是靜止坐標系下的定子電感矩陣;[eα1eβ1eα3eβ3]T是靜止坐標系下的反電勢矢量。由于電機為表貼非凸極結構,Ld1=Lq1=Lα1=Lβ1,Ld3=Lq3=Lα3=Lβ3。

將(1)式轉換為電流狀態方程形式,并根據相關的滑模變結構理論,則考慮三次諧波的五相永磁同步電機滑模觀測器設計如下：

(2)

(3)

式中,a為sigmoid函數的斜率,是一個可調正實數。

其后定義滑模面如(4)式所示：

(4)

為了證明所設計滑模觀測器的穩定性,定義李雅普諾夫函數如(5)式所示：

(5)

根據李雅普諾夫穩定性判據,如果所設計的滑模觀測器(2)穩定且收斂于滑模面S(X),那么李雅普諾夫函數V1需同時滿足如下2個條件:①李雅普諾夫函數V1正定;②李雅普諾夫函數V1的導數為負數。由(5)式可以看出,由于所定義的李雅普諾夫函數為靜止坐標系α1-β1-α3-β3下定子電流估計誤差平方和的形式,顯然滿足條件①。那么只需要證明李雅普諾夫函數V1的導數為負數,則可證明所設計滑模觀測器的穩定性,即

(6)

為了證明李雅普諾夫函數的導數為負數,通過(2)式與(1)式轉換的電流狀態方程相減,可以得到定子電流誤差方程如(7)式所示：

(7)

將(7)式代入(6)式,滑模觀測器李雅普諾夫函數的導數可表示如(8)式所示：

(8)

由于所有狀態變量和電機參數均有界,因此,通過式(8)可以推導出所設計的五相永磁同步電機無位置傳感器滑模觀測器的收斂條件為

(9)

只要滿足(9)式的條件,則可證明所設計滑模觀測器的穩定性,即選擇合適的滑模增益k1和k2,則可使滑模觀測器穩定并收斂。

當滑模觀測器系統達到滑模面時有

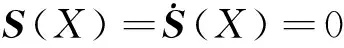
(10)

將(10)式代入(7)式,可得到電機反電勢如下：

(11)

2.2 反電勢自適應觀測器設計

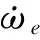
式中,ωe是轉子電角速度,θ是轉子位置電角度,Ψm1是基波磁鏈幅值。

基于(12)式和相關的自適應觀測器設計理論,五相永磁同步電機無位置傳感器驅動控制系統的自適應反電勢觀測器設計如下

(13)

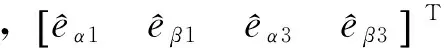
用(13)式減去(12)式,可以得到五相永磁同步電機的反電勢估計誤差方程

(14)

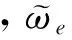
為了證明所設計的反電勢自適應觀測器的穩定性,定義反電勢自適應觀測器的李雅普諾夫函數如(15)式所示

(15)

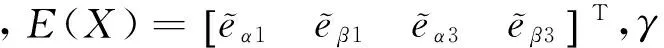
(16)

(17)

將(14)式代入(17)式可得

(18)

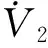
(19)

從(19)式中,可以得到反電勢觀測器的自適應律如如(20)式所示

(20)

又因為

(21)

所以,五相永磁同步電機的轉子位置和轉子電角速度估計值如(22)式所示

(22)

3 仿真實驗及分析

為了驗證所提出的滑模自適應觀測器的效果,利用Matlab/Simulink仿真軟件,搭建了如圖1所示的五相永磁同步電機無位置傳感器驅動控制系統。通過仿真實驗,對比驗證了常規滑模觀測器與所提出的滑模自適應觀測器,在額定轉速和突加負載轉矩的條件下,對電機轉速、轉子位置以及基波反電勢和三次諧波反電勢的估計效果,并對仿真實驗結果進行了詳細分析。仿真實驗中的五相永磁同步電機參數和滑模自適應觀測器參數如表1和表2所示。

表1 五相永磁同步電機參數

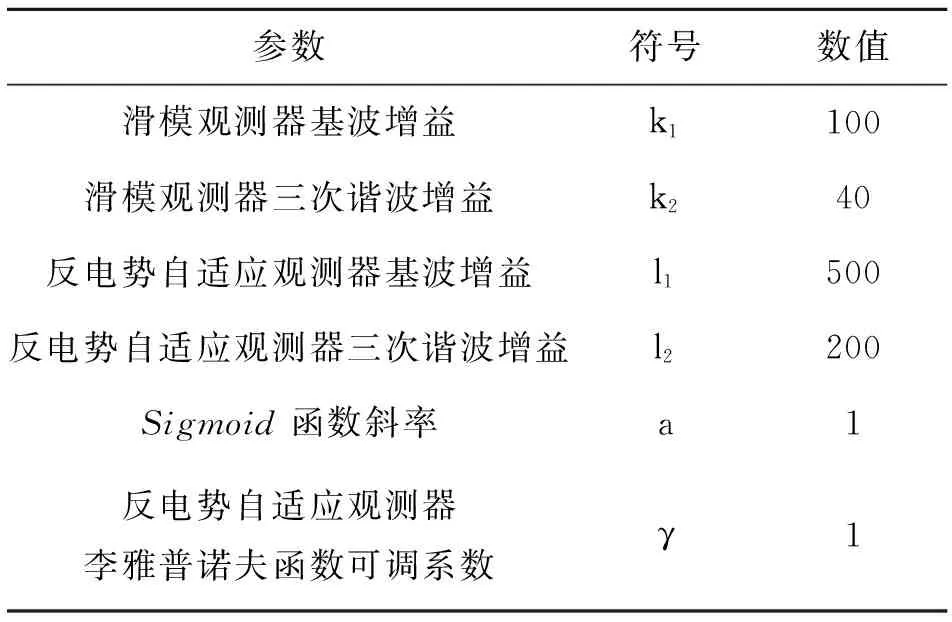
表2 自適應滑模觀測器參數

圖3～圖6為常規滑模觀測器在額定轉速和突加負載轉矩條件下的轉速、轉子位置、反電勢基波以及反電勢三次諧波波形;圖7～圖10為所提出的自適應滑模觀測器在額定轉速和突加負載轉矩條件下的轉速、轉子位置、反電勢基波以及反電勢三次諧波波形。2種滑模觀測器均測試于相同條件下,電機給定轉速900 r/min,加減速速率為±1 000 r/s,并在1.2 s時,負載轉矩階躍至11 Nm。通過對比圖3和圖7可以看出,常規滑模觀測器在電機轉速估計過程中的滑模抖振明顯大于所提出的自適應滑模觀測器。對比圖4～圖6和圖8～圖10中相對應的波形,可以看出在電機轉子位置信號、基波反電勢和三次諧波反電勢的估計過程中,常規滑模觀測器的抖振現象相對于自適應滑模觀測器仍然較為明顯。通過計算和分析,所提出的自適應滑模觀測器在電機轉速估計過程中的最大瞬態估計誤差為0.1%且在穩態時收斂至零,而常規滑模觀測器的轉速估計最大誤差為0.5%。此外,自適應滑模觀測器在電機轉子位置估計過程中的最大瞬態估計誤差為0.05%,主要產生在每個2π弧度之間的位置信號的連續變換

瞬間,而常規滑模觀測器的轉子位置估計最大誤差為0.1%。與常規滑模觀測器相比,所提出的自適應滑模觀測器在五相永磁同步電機無位置傳感器驅動控制系統中具有更好的轉速和位置跟蹤效果,以及較強的抗負載擾動能力。

圖3 常規滑模觀測器實際轉速和估計轉速波形

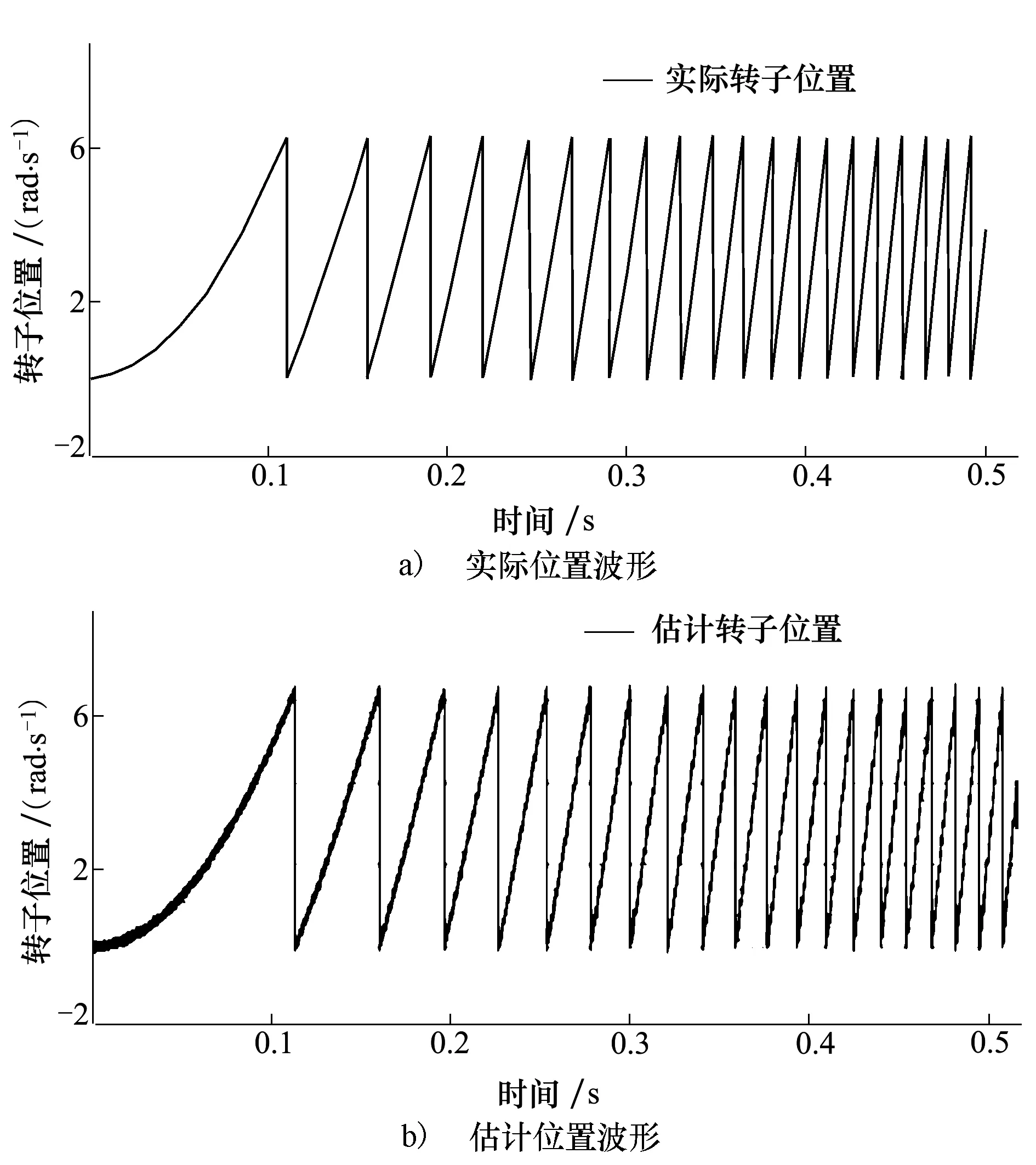
圖4 常規滑模觀測器實際轉子位置和估計轉子位置波形

圖5 常規滑模觀測器反電勢基波分量估計波形 圖6 常規滑模觀測器反電勢三次諧波分量估計波形

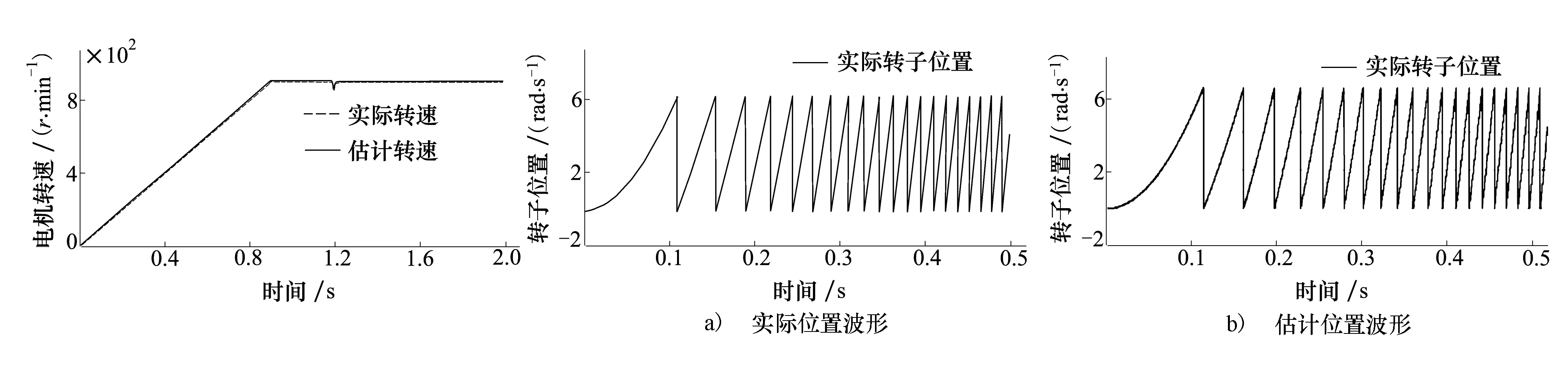
圖7 自適應滑模觀測器實際圖8 自適應滑模觀測器實際轉子位置和估計轉子位置波形轉速和估計轉速波形

圖9 自適應滑模觀測器反電勢基波分量估計波形 圖10 自適應滑模觀測器反電勢三次諧波分量估計波形

4 結 論

本文提出了一種基于自適應滑模觀測器的五相永磁同步電機無位置傳感器控制方法。該方法在考慮三次諧波對五相永磁同步電機影響的條件下,首先利用五相永磁同步電機模型設計了滑模觀測器,并用sigmoid函數代替了一般滑模觀測器常用的符號函數作為電流觀測器的開關函數,以減小滑模抖動并獲得更為準確的反電勢當量信號。其次設計了反電勢自適應觀測器來估計電機轉速和位置信號,消除了常規無位置傳感器控制系統中滑模觀測器所必需的低通濾波器和相位補償單元,提高了轉速和位置信號的估計精度。此外,利用李雅普諾夫準則,證明了所設計的滑模觀測器和反電勢自適應觀測器的穩定性。仿真結果顯示,與常規滑模觀測器相比,所提出的自適應滑模觀測器在五相永磁同步電機無位置傳感器控制系統中抖動更小,轉速和位置估計誤差更小,反電勢估計更為準確,且能運行在多種復雜條件下,具有較強的魯棒性,適合應用于五相永磁同步電機無位置傳感器驅動控制系統。

[1] Nguyen N, Meinguet F, Semail E, et al. Fault-Tolerant Operation of an Open-End Winding Five-Phase PMSM Drive with Short-Circuit Inverter Fault[J]. IEEE Trans on Industrial Electronics, 2016, 63(1): 595-605

[2] Mohammadpour A, Parsa L. Global Fault-Tolerant Control Technique for Multiphase Permanent-Magnet Machines[J]. IEEE Trans on Industry Applications, 2015, 51(1):178-186

[3] Mohammadpour A, Parsa L. A Unified Fault-Tolerant Current Control Approach for Five-Phase PM Motors With Trapezoidal Back EMF Under Different Stator Winding Connections[J]. IEEE Trans on Power Electronics, 2013, 28(7):3517-3527

[4] Trabelsi M, Nguyen N K, Semail E. Real-Time Switches Fault Diagnosis Based on Typical Operating Characteristics of Five-Phase Permanent-Magnetic Synchronous Machines[J]. IEEE Trans on Industrial Electronics, 2016, 63(8): 4683-4694

[5] Pacas M. Sensorless Drives in Industrial Applications[J]. IEEE Industrial Electronics Magazine, 2011, 5(2):16-23

[6] Buccella C, Cecati C, Latafat H. Digital Control of Power Converters-A Survey[J]. IEEE Trans on Industrial Informatics, 2012, 8(3):437-447

[7] Ramezani M, Ojo O. The Modeling and Position-Sensorless Estimation Technique for A Nine-Phase Interior Permanent-Magnet Machine Using High-Frequency Injections[J]. IEEE Trans on Industry Applications, 2016, 52(2): 1555-1565

[8] Wang G, Zhan H, Zhang G, et al. Adaptive Compensation Method of Position Estimation Harmonic Error for EMF-Based Observer in Sensorless IPMSM Drives[J]. IEEE Trans on Power Electronics, 2014, 29(6):3055-3064

[9] Guo L, Parsa L. Model Reference Adaptive Control of Five-Phase IPM Motors Based on Neural Network[J]. IEEE Trans on Industrial Electronics, 2012, 59(3): 1500-1508

[10] Quang N K, Hieu N T, Ha Q P. FPGA-Based Sensorless PMSM Speed Control Using Reduced-Order Extended Kalman Filters[J]. IEEE Trans on Industrial Electronics, 2014, 61(12):6574-6582

[11] Wang G, Li T, Zhang G, et al. Position Estimation Error Reduction Using Recursive-Least-Square Adaptive Filter for Model-Based Sensorless Interior Permanent-Magnet Synchronous Motor Drives[J]. IEEE Trans on Industrial Electronics, 2014, 61(9):5115-5125

[12] Gao, Y, Liu W G, Yang Q. Study of Position Sensorless Control Based on Sliding Mode Observer[C]∥International Conference on Electrical Machines and Systems, 2011:1-3

[13] Lee H, Lee J. Design of Iterative Sliding Mode Observer for Sensorless PMSM Control[J]. IEEE Trans on Control Systems Technology, 2013, 21(4):1394-1399

[14] Qiao Z, Shi T, Wang Y, et al. New Sliding-Mode Observer for Position Sensorless Control of Permanent-Magnet Synchronous Motor[J]. IEEE Trans on Industrial Electronics, 2013, 60(2):710-719

Adaptive Sliding Mode Observer for Sensorless Control of Five-Phase Permanent Magnet Synchronous Motor

Yang Jianwei, Dou Manfeng, Zhao Dongdong, Yan Liming

(School of Automation, Northwestern Polytechnical University, Xi′an 710072, China)

For the impact of the third harmonic, the sensorless control method for three-phase permanent magnet synchronous motor (PMSM) can′t be applied for five-phase PMSM directly. This paper investigates the position sensorless control problem of five-phase PMSM drive system based on an adaptive sliding mode observer (ASMO) with the consideration of the third harmonic voltage and current. First, a sliding mode current observer is designed based on the five-phase PMSM model with the third harmonic by replacing the conventional sign function with the sigmoid function as the switching function to reduce the chattering and obtain the equivalent signal of the back electromotive force (EMF). Then, an adaptive observer of back EMF is built to estimate the back EMF, the velocity and the rotor position of five-phase PMSM, which eliminates the low-pass filter and phase compensation module in sensorless control system and improves the estimation accuracy. Meanwhile, the stability of the sliding current observer and the back EMF adaptive observer is demonstrated in detail by Lyapunov stability criteria and the simulation is done by Matlab/Simulink. The simulation results show that compared with the conventional SMO, the proposed ASMO is with less chattering, small errors of rotor speed and position, more accurate estimated value of back EMF and strong robustness.

five-phase permanent magnet synchronous motor (five-phase PMSM), sensorless control, adaptive sliding mode observer (ASMO), Lyapunov stability criteria, Lyapunov functions, angular velocity, MATLAB

2016-09-08

國家自然科學基金(51507143)與陜西省工業科技攻關項目(2015GYT090)資助

楊劍威(1986—)，西北工業大學博士研究生，主要從事電機驅動控制及電力電子方向的研究。

TM351

A

1000-2758(2016)06-1057-08