一類非線性分數階微分方程邊值問題正解的存在性*

康文彥，高巧琴

(呂梁學院數學系，山西呂梁033000)

一類非線性分數階微分方程邊值問題正解的存在性*

康文彥，高巧琴

(呂梁學院數學系，山西呂梁033000)

通過運用Avery－Peterson不動點定理，得到了一類非線性分數階微分方程邊值問題至少有三個正解的充分條件.最后，通過一個具體實例驗證了給出的充分條件的正確性.

分數階微積分;分數階邊值問題;格林函數;Avery－Peterson不動點定理;錐

近些年來對分數階微積分和分數階微分方程邊值問題的研究被許多學者所關注［1］.在文獻［2］中，通過運用Amann定理和上下解的方法研究了一類帶有非線性邊值條件的分數階微分方程邊值問題，得到了其存在多解的新結果.在文獻［3］中，通過運用半序集上的不動點理論，證明了非線性分數階微分方程的邊值問題解的存在性和唯一性.在文獻［4］中，應用Leray－Shauder非線性擇決和錐上的Krasnoselskii不動點理論，證明了非線性分數階微分方程的邊值問題正解的存在性.在文獻［5］中，通過運用錐上的不動點定理，證明了的正解的存在性，其中Dα表示標準的Riemann－Liouville型分數階微分.在文獻［6］中，應用錐上Avery－Peterson不動點定理，證明了一類非線性Caputo分數階微分方程邊值問題至少有三個解的存在性問題.

本文通過運用格林函數的性質和錐上Avery－Peterson不動點定理，得到邊值問題至少有三個正解存在的結果.

1 預備知識

定義1 設α＞0，函數(0，+∞)→R連續，則分數階積分定義為

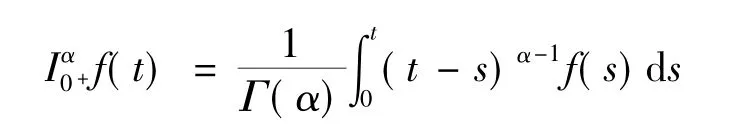
定義2 設α＞0，函數(0，+∞)→R連續，則分數階右側Caputo導數定義為

其中n=［α］+1.

引理1［4］令α＞0，若u(t)∈ACn［0，1］或u(t)∈Cn［0，1］，那么

其中n=［α］+1

引理2［5］令g(t)∈C［0，1］，則邊值問題

有唯一解u(t)=∫10G(t，s)g(s)d s，其中G(t，s)=

這里G(t，s)是邊值問題(2)的格林函數.

引理3 格林函數G(t，s)有如下性質:

(i)G(t，s)∈C(［0，1］×［0，1］)且對任意的t，s∈(0，1)，G(t，s)＞0;

定義3 稱映射φ是Banach空間E中錐P上的非負連續的凸函數，若φ滿足:φ:P→［0，∞)是連續的且φ(tx+(1－t)y)≥tφ(x)+(1－t)φ(y)，其中x，y∈P，t∈［0，1］.

令γ，θ是錐P上非負連續的凸函數，φ是錐P上非負連續的凹函數，ψ是錐P上的非負連續函數，則對正數a，b，c，d，定義下面的凸集:

引理4 令P是Banach空間E中的一個錐，γ，θ是錐P上非負連續的凸函數，φ是錐P上非負連續的凹函數，ψ是錐P上的非負連續函數，滿足:

ψ(λx)≤λψ(x)，λ∈［0，1］

(S1)當x∈P(γ，θ，φ，b，c，d)時，{x∈P(γ，θ，φ，b，c，d)|φ(x)＞d}≠?，且φ(Tx)＞b;

(S2)當x∈P(γ，θ，φ，b，d)且θ(Tx)＞c時，φ(Tx)＞b;

(S3)當x∈R(γ，θ，a，d)，且ψ(x)=a時，0?R(γ，φ，a，d)且ψ(Tx)＜a成立.那么T至少有三個不動點x1，x2，x3∈P(β，d)使得γ(xi)≤d，i=1，2，3;b＜φ(x1);a＜ψ(x2);φ(x2)＜b;ψ(x3)＜a.

2 主要結果

引理5 假設f(t，u(t)，u'(t))＞0，u(t)是邊值問題(1)的一個解，那么‖u‖≤‖u'‖.

定義算子T:K→E為

引理6 假設f(t，u，u')在［0，1］×［0，+∞)× R是連續的，那么映射T:K→K是全連續的.

證明 由f:［0，1］×［0，+∞)×R→［0，+∞)和引理3可知Tu(t)＞0.又因為

所以T(K)?K，則T是全連續的.

令α是非負連續的凹函數，β、θ是非負連續的凸函數，φ、ψ是非負連續函數，它們在錐上定義如下:β(u)=‖u'‖，θ(u)=ψ(u)=‖u‖，φ(u)=|u(t)|.由引理5和6可知，以上定義的函數滿足θ(u)≤ φ(u)≤ θ(u) =ψ(u)，‖u‖ ≤β(u)，u∈K.

假設存在正的常數a，b，d且a＜b＜d，c=4b使得

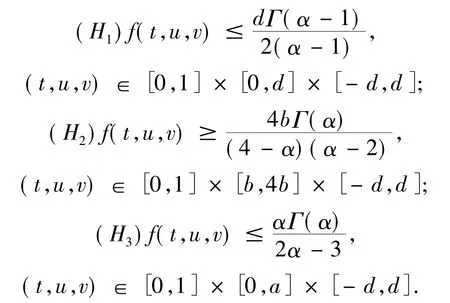
定理1 假設(H1)～(H3)成立，則邊值問題至少有三個正解u1，u2，u3滿足u1(t)

證明 該邊值問題有解u=u(t)當且僅當u是算子方程

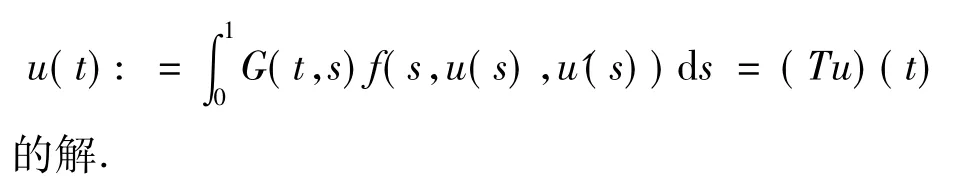
事實上常函數u(t)=4b∈P(β，θ，φ，b，c，d)和φ(4b)＞b暗含{u∈P(β，θ，φ，b，c，d)|φ(u)＞b}≠?.對u∈P(β，θ，φ，b，c，d)，有b≤u(t)≤4b，且對t∈有|u'(t)|＜d.由假設(H2)知暗含對任意的u∈P(β，θ，φ，b，c，d)有φ(Tu)＞b.

由ψ(0)=0可知0?R(β，ψ，a，d)，假設u∈R(β，ψ，a，d)，ψ(u)=a，那么由假設H3可知

因而，引理4的所有條件都滿足.所以該邊值問題至少有三個正解u1，u2，u3滿足‖ui‖ ＜d，i=1，＜b;‖u3‖ ＜a.

3 例子

考慮下面FBVP

其中α=1.5，t∈［0，1］.選擇a=1，b=10，d=104，于是.則非線性項f(t，u，u')滿足

由定理1知邊值問題(2)至少有三個正解u1，u2，u3滿足

［1］V Lakshmikantham，A S Vatsala.Basic theory of fractional differential equations［J］.Nonlinear Anal，2008，69:2677－2682.

［2］Liu Xiping，Jia Mei.Multiple solutions for fractional differential equations with nonlinear boundary conditions［J］.Computers and Mathematics with Applications，2010，59:2880－2886.

［3］Mena J C，Harjani J.Existence and uniqueness of positive and nondecreasing solutions for a class of singular fractional boundary value problems［J］.Boundary Value problems，2009，43:1011－1016.

［4］Bai Zhanbing，Qiu Tingting.Existence of positive solution for singular fractional differential equation［J］.Applied Mathematics and Computation 2009，215:2761－2767.

［5］Xiong Yang，Zhongli Wei，Wei Dong.Existence of positive solutions for the boundary value problem of nonlinear fractional differential equations［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17(1):85－92.

［6］Liu Yang.Application of Avery－Peterson fixed point theorem to nonlinear boundary value problem of fractional differential equation with the Caputo's derivative［J］.Commun Nonlinear Sci NumerSimulat，2012，17:4576－4584.

(責任編輯:陳衍峰)

O175

A

1008－7974(2016)06－0028－03

10.13877/j.cnki.cn22－1284.2016.12.009

2016－07－12

國家青年科學基金項目“糾纏及糾纏之外的量子關聯刻畫”(11301312);校內青年基金項目“三維空間一類齊次Moran集的Hausdorff維數”(ZRQN201521);校級科研基金項目“分數階差分方程邊值問題解的存在性”(2014Q10)

康文彥，女，山西呂梁人，教師.